Single Plate Shear Connections (AISC)
This verification example was prepared by Mark D. Denavit and Kayla Truman-Jarrell in a joint project of The University of Tennessee and IDEA StatiCa.
1 Description
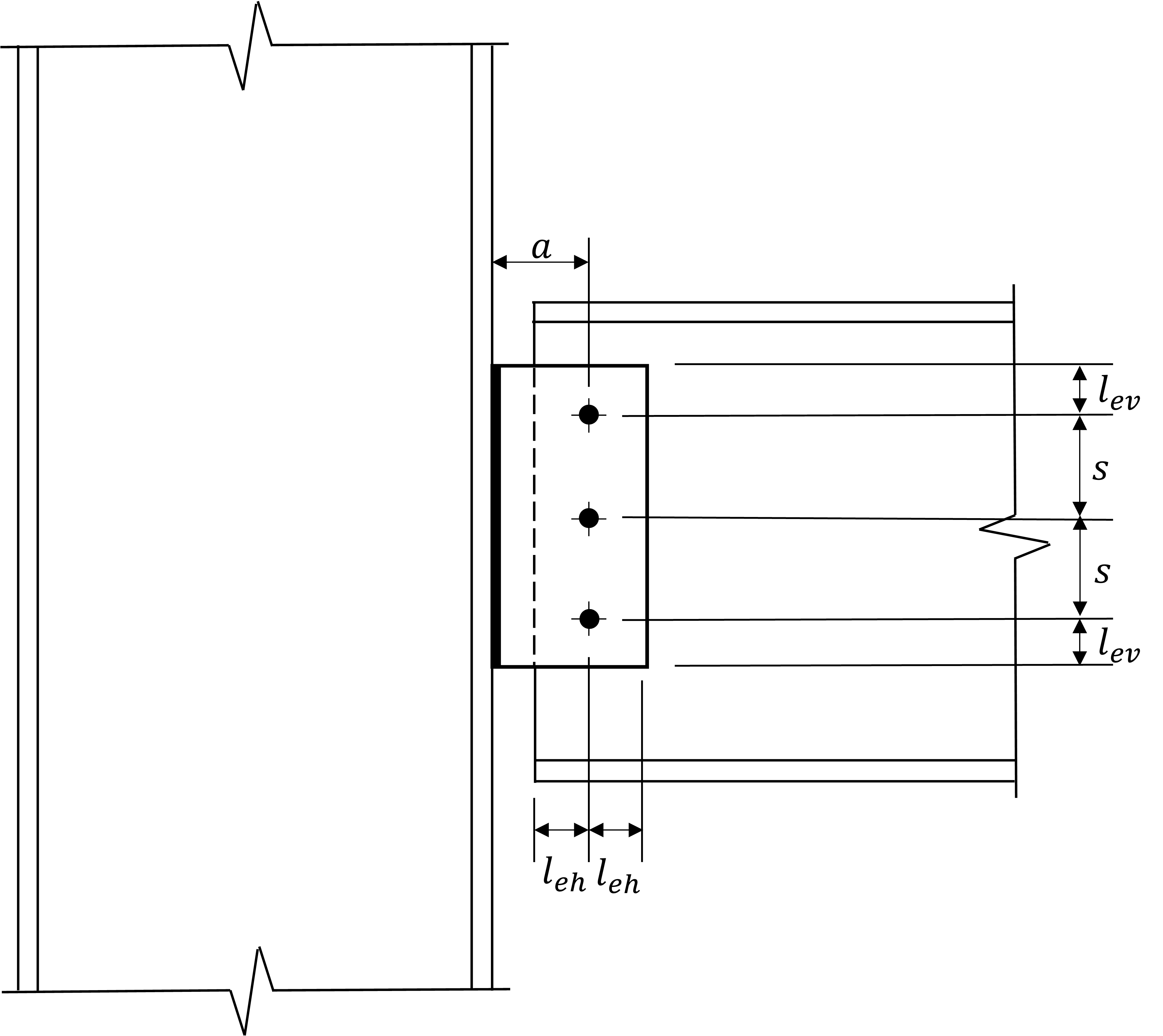
A comparison between results from the component-based finite element method (CBFEM) and traditional calculation methods used in US practice for single plate shear connections is presented in this section. A schematic of the connection investigated is presented in Fig. 1.
Fig. 1 Schematic of single plate shear connection.
The traditional calculation methods used in this work are based upon the recommendations presented in Part 10 of the AISC Manual (2017). Two approaches for the design of single plate shear connections are presented in Part 10 of the AISC Manual. The first, for “conventional” configurations, offers some simplifications if certain dimensional limitations are met. The second, for “extended” configurations, is more broadly applicable but without the simplifications permitted for the design of conventional configurations. Specifically, conventional configurations must have a single vertical row of between 2 and 12 bolts, the distance between the bolt line and the weld line, a, must be equal to or less than 3.5 in., bolts must be in standard holes or short-slotted holes transverse to the member reaction, the vertical edge distance, lev, must satisfy the minimum edge distance requirements of Table J3.4 of the AISC Specification (2016), the horizontal edge distance, leh, must be greater than or equal to 2d, where d is the bolt diameter, and either the thickness of the plate, tp, or the thickness of the beam web, tw, must satisfy maximum thickness requirements.
The primary simplification to design for connections that meet these requirements is that bolt group strength may be evaluated as follows: bolt shear strength checked using the eccentricity listed in Table 10-9 of the AISC Manual (2017) and bearing and tearout checked assuming the reaction is applied concentrically. This simplification avoids the need to consider tearout in an eccentrically loaded bolt group. For extended configuration calculations, where tearout is considered when determining the strength of the eccentrically loaded bolt group, two different methods are employed. The first method is a commonly used conservative approximation known as the “poison bolt” method. In this method, the strength of the eccentrically loaded bolt group is obtained by identifying the smallest possible strength for any of the bolts for any direction of force then utilizing that value of strength in conjunction with a value of C from the tables in Part 7 of the AISC Manual (2017). The values of C listed in the tables are computed from the instantaneous center of rotation (IC) method. The second method is to use the modified instantaneous center of rotation method developed by Denavit et al. (2021) in which tearout is considered explicitly within the iterative procedure for determining the strength of the bolt group.
Beyond bolt group strength, shear yielding of the plate, shear rupture of the plate, block shear rupture of the plate, and weld shear are also checked for conventional configurations. Additional checks for extended configurations include those for flexural rupture, plate interaction strength, and plate buckling.
All traditional calculations were performed in accordance with the provisions for load and resistance factor design (LRFD) in the AISC Specification (2016).
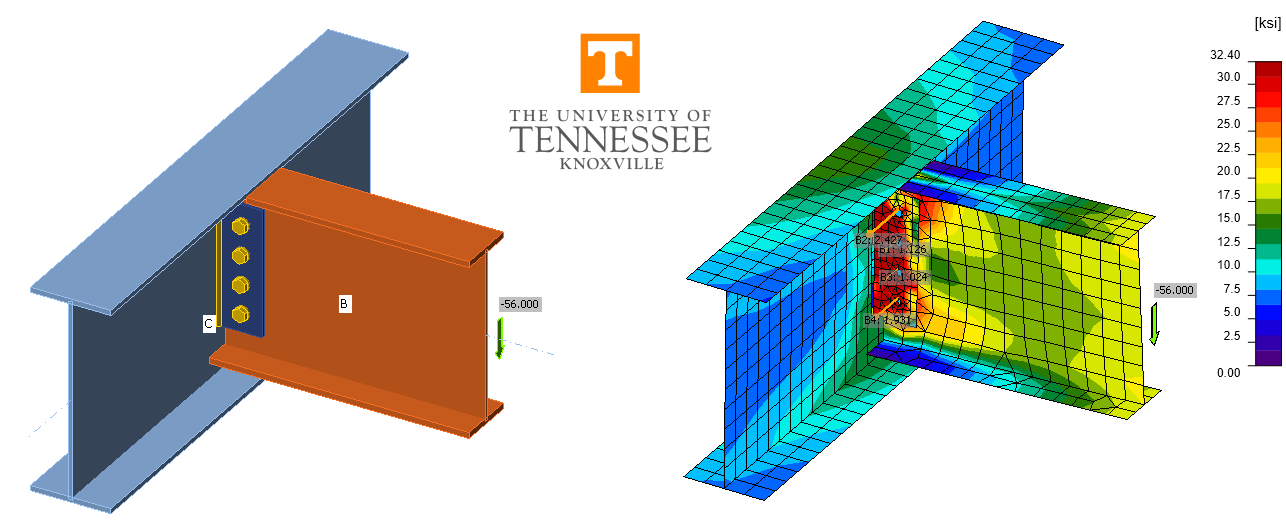
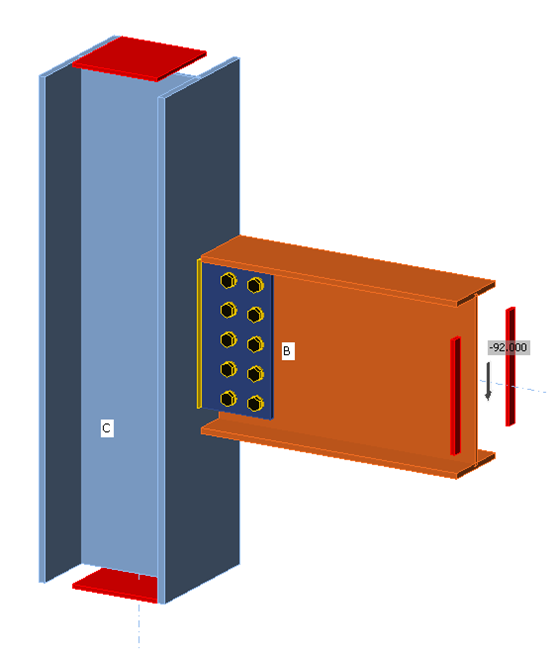
The CBFEM results were obtained from IDEA StatiCa Version 21.0. An example model is shown in Fig. 2. The maximum permitted loads were determined iteratively by adjusting the applied load input to a value that the program deems safe but if increased by a small amount (e.g., 0.1 kip) the program would deem unsafe. In all models, the supported beam was assigned a “N-Vz-My” model type to ensure in-plane behavior. Unless noted otherwise, forces were defined such that the point of zero moment was located at the weld line, matching the assumption of the design methods presented in Part 10 of the AISC Manual (2017).
Fig. 2 Single plate shear connection modeled in IDEA StatiCa.
2 Bolt Group Strength
First, connections, where the strength of the bolt group controls the strength of the connection, are investigated. For these comparisons the column is a W14x90, and the supported beam, which frames into the flange of the column, is a W18x50. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The plate is 15 in. tall (s = 3 in., lev = 1.5 in.), 1/2 in. thick, and conforms to ASTM A36 (Fy = 36 ksi, Fu = 58 ksi). Each vertical row of bolts has (5) 3/4 in. diameter A325 bolts with threads not excluded from the shear plane and horizontal edge distance, leh = 2.0 in. The weld was a 5/16 in. fillet weld on both sides in accordance with the (5/8)tp rule noted in Part 10 of the AISC Manual (2017). The distance from the weld line to the bolt line, a, was varied from 2 in. to 5 in. (Fig. 3). Note that this connection satisfies the requirements for the conventional configuration when a ≤ 3.5 in.
Fig. 3 Variation of ‘a’ in the IDEA StatiCa model.
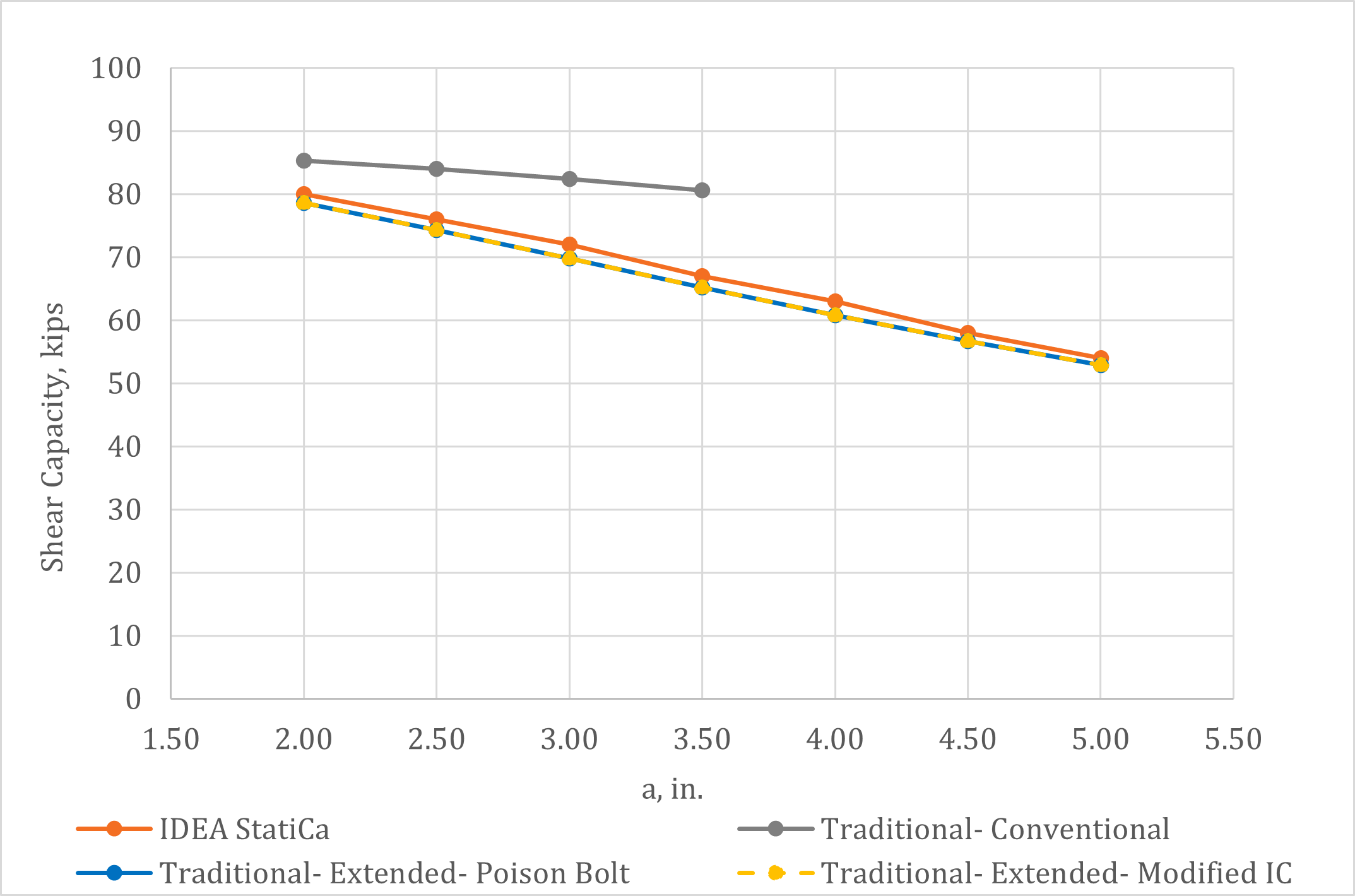
Variation of the shear capacity of the connections with the distance a is presented in Fig. 4. Bolt shear rupture was the controlling limit state for all values of a and all methods of calculation. The IDEA StatiCa results match well with the traditional calculations for the extended configuration. Where applicable, the traditional calculations for the conventional configuration give somewhat greater shear capacity. The reason for this is that a reduced eccentricity of a/2 is permitted to be assumed for conventional configurations per Table 10-9 of the AISC Manual (2017). The eccentricity of the bolt group is taken as a for the extended configuration calculations. The eccentricity of the bolt group is also equal to a for IDEA StatiCa because the point of zero moment was defined to be at the weld line. The poison bolt method and the modified IC method provide the same results indicating that tearout did not control for any bolt (i.e., the plate and beam web were sufficiently thick and the bolt spacing and edge distances were sufficiently large).
Fig. 4 Shear capacity of single plate shear connection with respect to ‘a’.
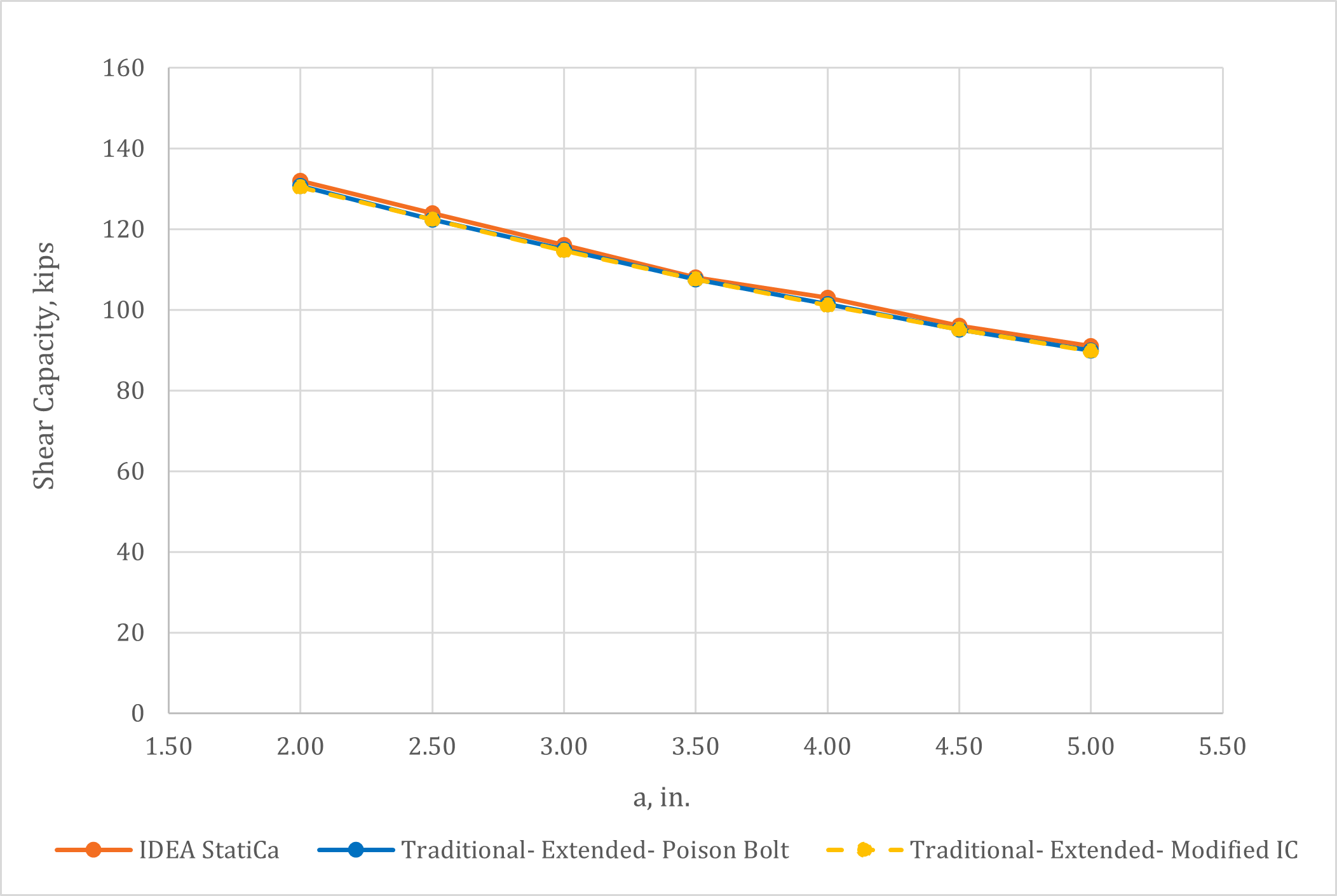
Variation of the shear capacity with the distance a is presented in Fig. 5 for connections with the same properties as previously described but with two vertical rows of bolts (Fig. 6) and leh = 1.5 in. The horizontal spacing between vertical rows of bolts was 3 in. These connections are extended configuration regardless of the value of a given that they have more than one vertical row of bolts. Again, bolt shear rupture was the controlling limit state for all values of a and all methods and the IDEA StatiCa results match well with the traditional calculations.
Fig. 5 Shear capacity of extended configuration with two rows of bolts with respect to ‘a’.
Fig. 6 Extended Configuration with 2 rows of bolts modeled in IDEA StatiCa.
3 Plate Thickness
Varying the plate thickness allows for a wider range of limit states to control, including bearing and tearout at the bolt holes and shear yielding and rupture of the plate. For these comparisons the column is a W14x90 and the supported beam, which frames into the flange of the column, is a W18x130. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The plate is 14 in. tall (s = 3 in., lev = 1 in.) and conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi). The thickness of the plate varies from 3/16 in. to 3/4 in. in these analyses. There is one vertical row of (5) 3/4 in. diameter A490 bolts with threads not excluded from the shear plane and horizontal edge distance, leh = 1.5 in. Fillet welds were provided on both sides of the plate with size varying with plate thickness in accordance with the (5/8)tp rule noted in Part 10 of the AISC Manual (2017). The distance from the weld line to the bolt line, a, was 3.0 in. These connections satisfy the requirements for the conventional configuration for plate thicknesses less than or equal to 7/16 in.
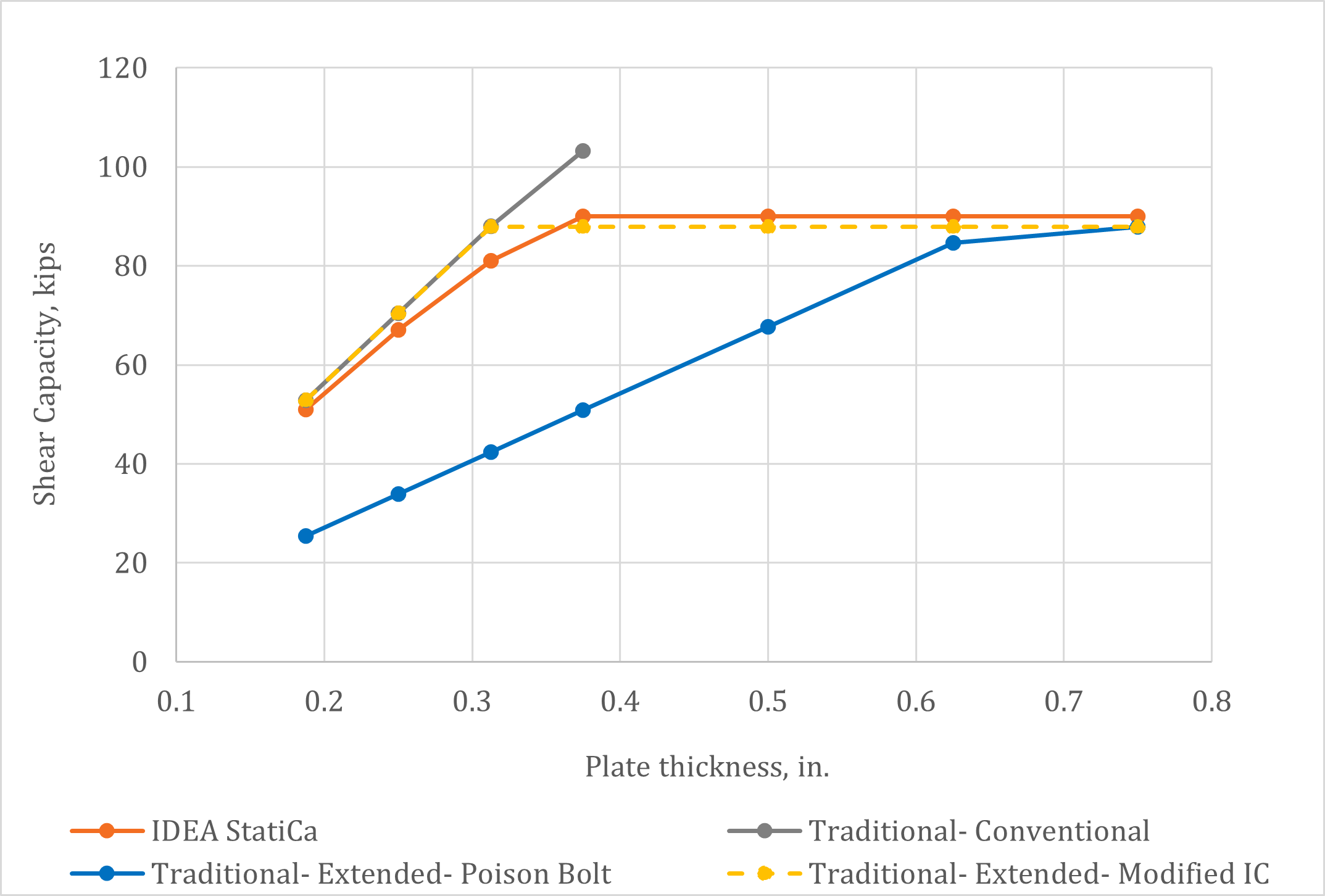
Variation of the shear capacity of the connections with plate thickness is presented in Fig. 7 with the controlling limit sates presented in Table 1. The most notable result is that the traditional calculations for the extended configuration using the poison bolt method show far lower strengths than the other methods. The poison bolt method, in which the lowest possible strength for any bolt is taken as the strength of every bolt, can be highly conservative. However, it is used in practice for the evaluation of eccentrically loaded bolt groups where tearout may control. For this connection, the strength of all the bolts is based on the tearout strength of the bottom bolt using an edge distance of lev = 1 in. resulting in a clear distance lc = 0.594 in. In IDEA StatiCa and the modified IC method, the strength of each individual bolt is based on the clear distance in the direction of force for that individual bolt. For example, at the limiting shear capacity of the connection with 1/4 in. thick plate, the clear distance for the bottom bolt computed by IDEA StatiCa is lc = 1.240 in. based on the angle of load in the bolt (Fig. 8b). Tearout strength is proportional to clear distance, so the strength of the bolts per IDEA StatiCa is significantly greater than assumed in the poison bolt method.
For the connections with the thinner plates, the plate controlled in both IDEA StatiCa and the traditional calculations (other than those using the poison bolt method). However, in IDEA StatiCa, plastic strains were concentrated at the holes of the top and especially the bottom bolts (Fig. 8). This contrasts with the assumed shear rupture failure plane used in the traditional calculations (i.e., a vertical line through the center of the bolts). Despite the differences in behavior, the resulting shear strength was close with IDEA StatiCa providing slightly lower shear capacities for the connections with the thinner plates.
Fig. 7 Shear Capacity of single plate shear connection with respect to plate thickness.
Table 1. Controlling limit state for results presented in Fig. 7
| Plate Thickness | IDEA StatiCa | Traditional Conventional | Traditional Extended (Poison Bolt) | Traditional Extended (Modified IC) |
| 3/16 in. | Plate strain | Plate shear rupture | Bolt group | Plate shear rupture |
| 1/4 in. | Plate strain | Plate shear rupture | Bolt group | Plate shear rupture |
| 5/16 in. | Plate Strain | Plate shear rupture | Bolt group | Bolt group |
| 3/8 in. | Bolt shear rupture | Bolt shear rupture | Bolt group | Bolt group |
| 1/2 in. | Bolt shear rupture | n/a | Bolt group | Bolt group |
| 5/8 in. | Bolt shear rupture | n/a | Bolt group | Bolt group |
| 3/4 in. | Bolt shear rupture | n/a | Bolt group | Bolt group |
Fig. 8 Detailed results for connection with 1/4 in. plate thickness.
4 Other Framing Configurations
Single plate shear connections are used for a variety of framing configurations. This section investigates two additional configurations, one where the supported beam frames into the web of a column and another where the supported beam frames into the web of a girder.
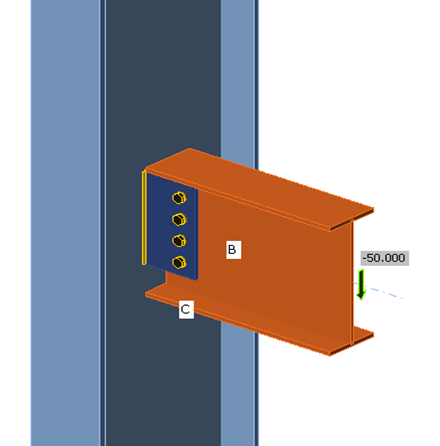
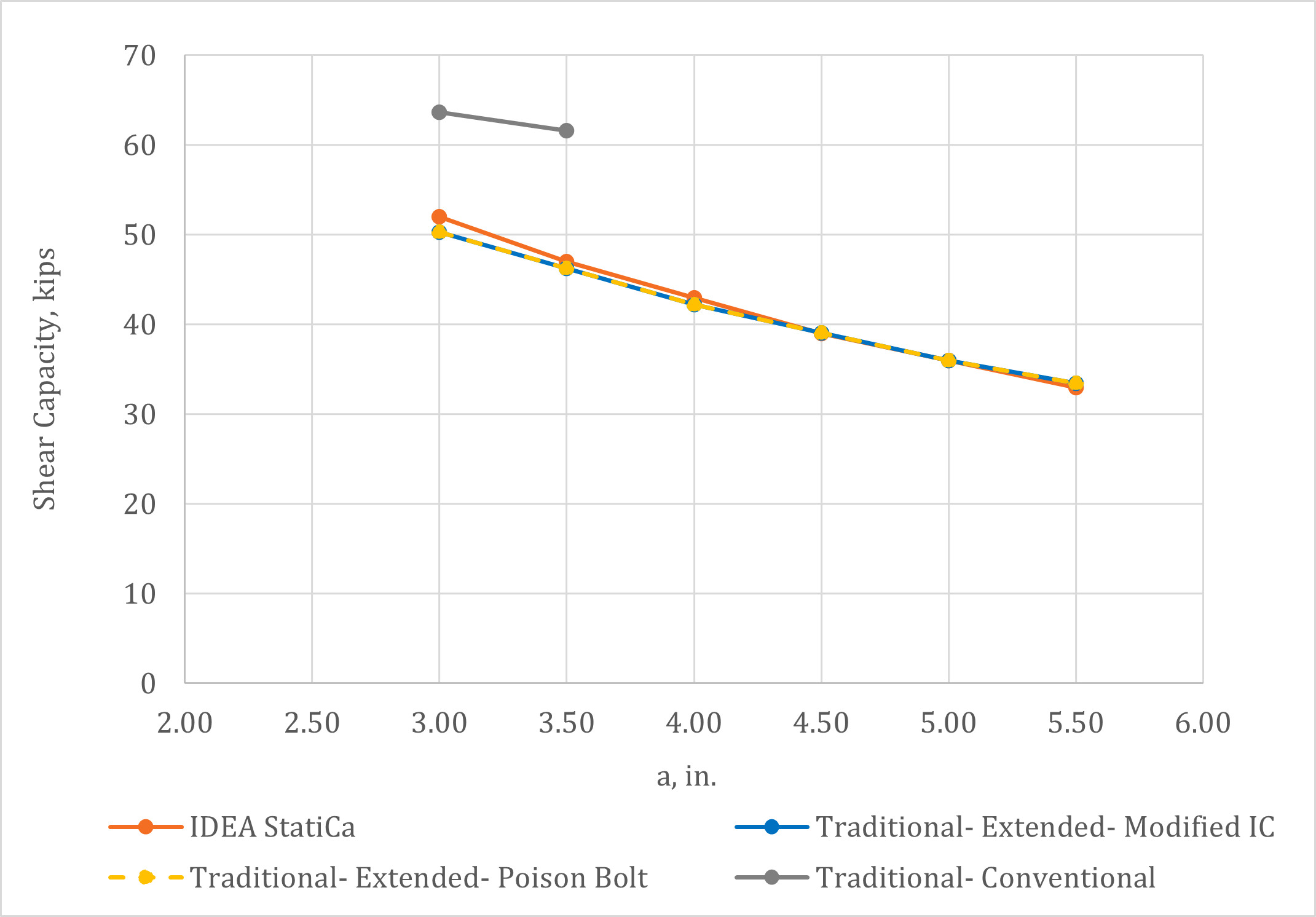
For the case of the supported beam framing into the web of a column (Fig. 9), the column is a W27x114, and the supported beam is a W18x50. For the case of the supported beam framing into the web of a girder (Fig. 11), the girder is a W21x55, and the supported beam is a W18x46. All wide flange shapes conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). For both cases, the plate is 13 in. tall (s = 3 in., lev = 2 in.), 3/8 in. thick, and conforms to ASTM A36 (Fy = 36 ksi, Fu = 58 ksi). The connections have a single vertical row of (4) 3/4 in. diameter A325 bolts with threads not excluded from the shear plane and horizontal edge distance, leh = 2 in. The weld was a 5/16 in. fillet weld on both sides of the plate. The distance from the weld line to the bolt line, a, was varied from 3 in. to 5.5 in.
Variation of the shear capacity of the connections with the distance a is presented in Fig. 10 for the case of the supported beam framing into the web of a column and Fig. 12 for the case of the supported beam framing into the web of a girder. Bolt shear rupture was the controlling limit state for all values of a and all methods in both framing configurations. The capacity determined from IDEA StatiCa agrees with that from the traditional calculations.
Fig. 9 IDEA StatiCa model of single plate shear connection welded to weak axis of column.
Fig. 10 Shear capacity of single plate shear connection welded to weak axis of column with respect to ‘a’.
Fig. 11 IDEA StatiCa model of single plate shear connection welded to beam web.
Fig. 12 Shear Capacity of single plate shear connection welded to beam web with respect to ‘a’.
5 Location of the Point of Zero Moment
The design methodology for single plate shear connections in Part 10 of the AISC Manual (2017) presumes that the location of the point of zero moment is at the weld line. Accordingly, all the IDEA StatiCa analyses thus far in this document have utilized an equivalent assumption for the position on the member from the node where the load is applied, X. However, other choices of the location of the point of zero moment could be made, especially if the choice is made consistently with the location of the pin in the structural analysis model of the frame.
Analyses were performed to investigate the impact of the location of the point of zero moment. For these analyses, the column is a W14x90, and the supported beam, which frames into the flange of the column, is a W18x143. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The plate is 14 in. tall (s = 3 in., lev = 1 in.), 3/8 in. thick, and conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi). There is one vertical row of (5) 3/4 in. diameter A490 bolts with threads excluded from the shear plane and horizontal edge distance, leh = 1 in. Fillet welds were provided on both sides of the plate with size varying with plate thickness in accordance with the (5/8)tp rule noted in Part 10 of the AISC Manual (2017). The distance from the weld line to the bolt line, a, was 9 in.
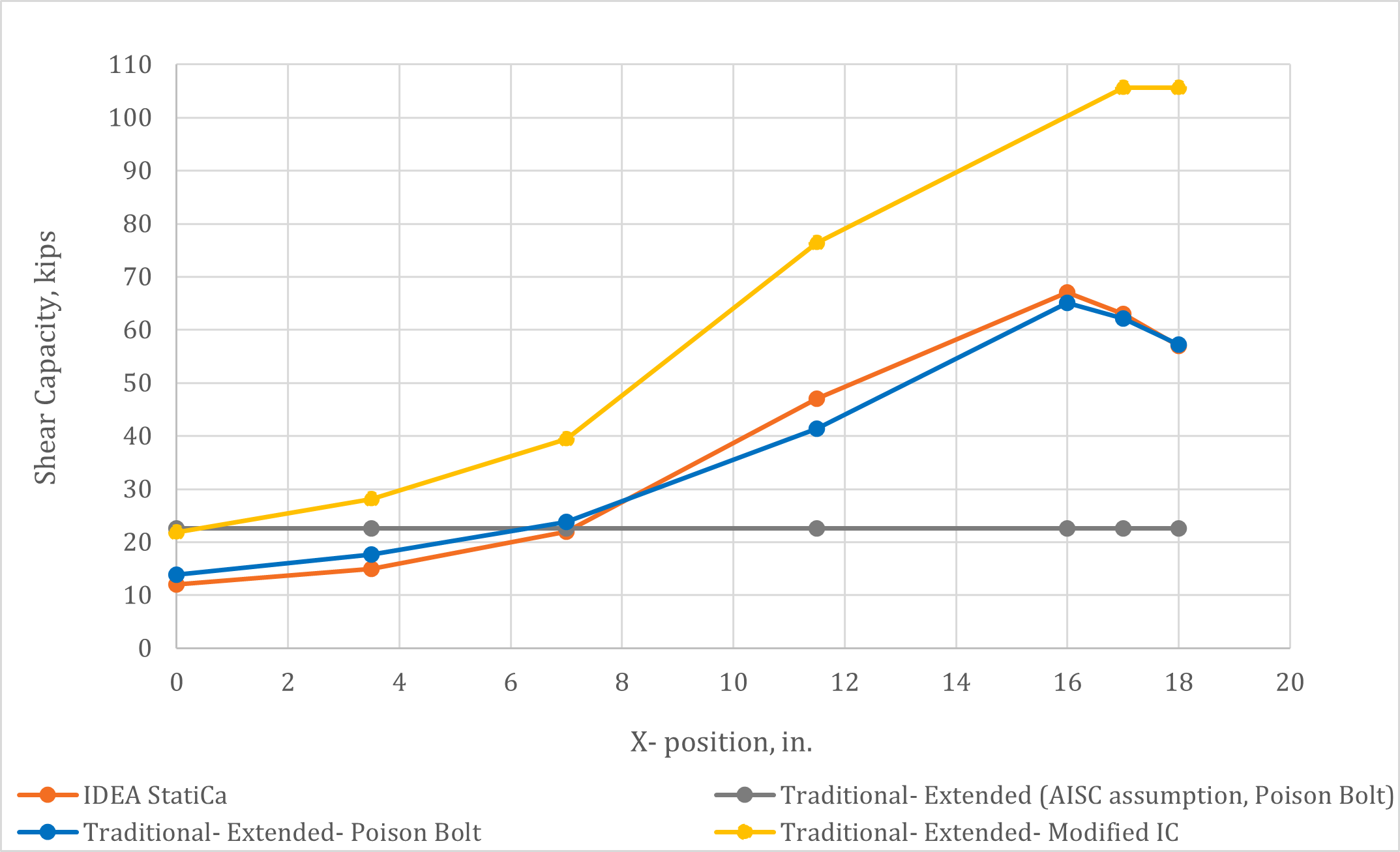
Variation of the shear capacity with the distance X (measured from the centerline of the column to the location of the point of zero moment) is presented in Fig. 13. The controlling limit state per IDEA StatiCa was bolt tearout for x ≤ 16 in. and weld resistance for greater values of X. The controlling limit states for the traditional calculations using the modified IC method were bolt group strength for x < 17 in. and shear rupture of the plate for greater values of X. The controlling limit state for the traditional calculations using the poison bolt method was bolt group strength for all values of X. It is interesting to note that the IDEA StatiCa results were near those from the poison bolt method for this comparison. For these cases, the direction of the force in the controlling bolt is near that of the worst-case condition used in the poison bolt method (Fig. 14).
Fig. 13 Shear capacity of single plate shear connection versus the location of the point of zero moment
Fig. 14 Detailed results for connection the position of the point of zero moment located at the weld line.
6 Stiffness Analysis
In addition to strength requirements, single plate shear connections must also satisfy rotation capacity requirements. Section B3.4a of the AISC Specification (2016) states that “a simple connection shall have sufficient rotation capacity to accommodate the required rotation determined by the analysis of the structure.” For the traditional calculations, this requirement is satisfied by maximum plate and beam web thickness limitations described in Part 10 of the AISC Manual (2017). With IDEA StatiCa, this requirement can be satisfied by performing a stiffness analysis.
The rotation capacities from a series of analyses on connections with varying plate thickness are presented in Fig. 15. For these analyses, the column is a W14x90, and the supported beam, which frames into the flange of the column, is a W18x130. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The plate is 15 in. tall (s = 3 in., lev = 1.5 in.) and conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi). There is one vertical row of (5) 7/8 in. diameter A325 bolts with threads not excluded from the shear plane and horizontal edge distance, leh = 1.5 in. Fillet welds were provided on both sides of the plate with size varying with plate thickness in accordance with the (5/8)tp rule noted in Part 10 of the AISC Manual (2017). The distance from the weld line to the bolt line, a, was 3 in. These connections satisfy the requirements for the conventional configuration and rotation capacity since all plate thicknesses are less than or equal to 1/2 in. (AISC Manual Table 10-9).
The analyses were performed using the ‘ST’ (stiffness) analysis type. Unlike the previous analyses, these models were loaded with bending moments about the major axis of the beam. The rotational capacity was independent of the magnitude of applied load.
Per Section B3.4a of the AISC Specification (2016) the required rotation capacity is determined from the structural analysis and depends on the framing and loads. A value of 0.03 rad or 30 mrad is commonly accepted as a reasonable upper bound for beam end rotation and the plate thickness limitations of Part 10 of the AISC Manual (2017) were calibrated to meet this upper bound (Muir and Thornton 2011). The rotation capacities shown in Fig. 15 are less than 30 mrad despite meeting the plate thickness requirements. The values may still be acceptable to a wide range of cases which have less beam end rotation than the upper bound, however, it is also possible that the stiffness analysis in IDEA StatiCa is not fully capturing the ductility of the connections.
Fig. 15 Rotation capacity with respect to varying plate thickness.
7 Summary
This study compared the design of single plate shear connections by traditional calculation methods used in US practice and IDEA StatiCa. Key observations from the study include:
- The available strength of single plate shear connections per IDEA StatiCa agrees well with traditional calculations using the method for extended configurations.
- The available strength per IDEA StatiCa was found to be conservative in comparison to the traditional calculations using the method for conventional configurations, which assumes a reduced eccentricity in some cases.
- IDEA StatiCa detects the clear distance for each bolt individually for consideration of tearout, resulting in appropriate reductions in strength when edge distances are small.
- IDEA StatiCa allows the investigation of different assumed locations of the point of zero moment.
- Stiffness analysis in IDEA StatiCa can be used to evaluate the rotation capacity requirements of AISC Specification Section B3.4a. However, the results were found to be conservative in comparison to the design rules presented in the AISC Manual for the cases examined.
8 References
AISC. (2016). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2017). Steel Construction Manual, 15th Edition. American Institute of Steel Construction, Chicago, Illinois.
Denavit, M. D., Franceschetti, N., and Shahan, A. (2021). Investigation of Bearing and Tearout of Steel Bolted Connections. Final Research Report to the American Institute of Steel Construction, Chicago, Illinois.
Muir, L. S., and Thornton, W. A. (2011). “The Development of a New Design Procedure for Conventional Single-Plate Shear Connections.” AISC Engineering Journal, 48(2), 141–152.