Lateral-torsional restraint in structural design
Model description
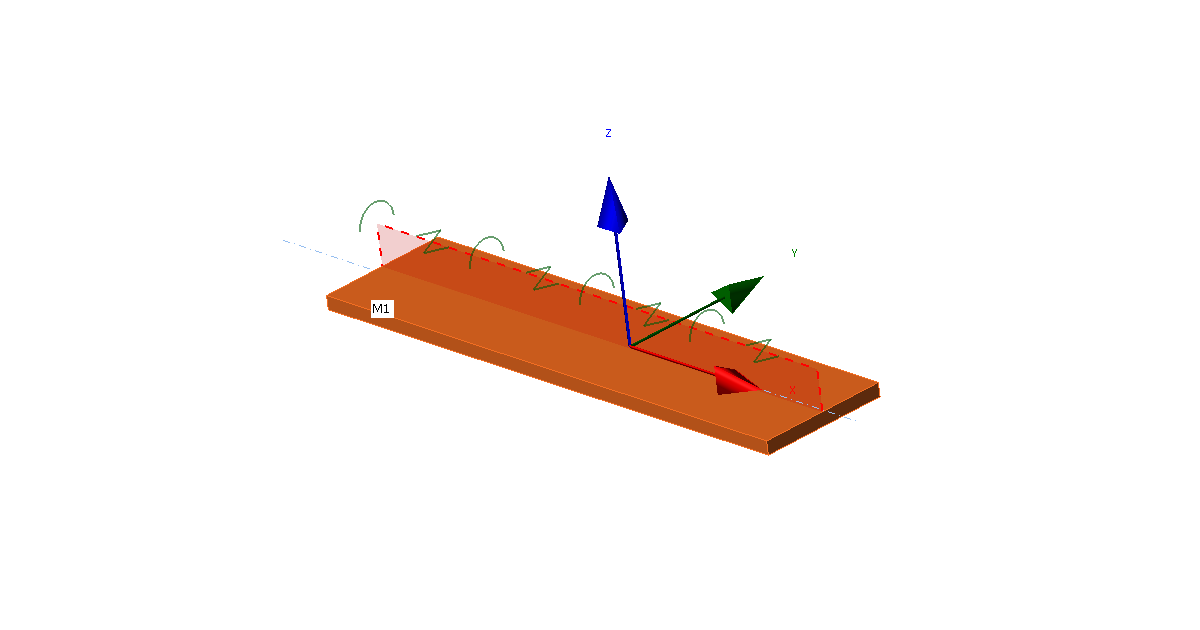
Lateral-torsional restraint is simulated by two stiffnesses added to any plate:
- Lateral (shear) S [N] applied in the direction of y axis of plate local coordinate system
- Torsional C [Nm/m] applied around x axis of a plate local coordinate system
Users may select any plate of a member, length of the restraint, type (continuous or discrete with set spacing), and lateral and torsional stiffnesses.
Local coordinate system of a plate with applied LTR
Nodes of finite elements are connected along the plate width by rigid body elements type 3 (RBE3) to one point at the plate longitudinal axis. Torsional stiffness is applied at this point by a special element with only one stiffness, rotation around x axis. This point is also connected by two other RBE3 with a special element between them with one stiffness, displacement in y axis.
The lateral stiffness is set by the user as free, rigid, or with set stiffness. Rigid stiffness is sufficiently high, set as 1000 times the shear stiffness of the plate. Stiffness \(S\) is set per unit length (one meter) with a force unit [N]. The stiffness of one element \(S_i\) has a force unit divided by length unit [N/m] and is then:
\[ S_i = \frac{S}{s_d} \]
where:
- \(s_d\) – distance between two points [m]
For discrete type, spacing is set directly by the user. For continuous type, the spacing is sufficiently small so that the behavior of the plate is not affected by spacing.
Similarly, the torsional stiffness is set by the user as free, rigid, or with set stiffness. Rigid stiffness is sufficiently high, set as 1 000 times the bending stiffness of the plate. Stiffness \(C\) is set per unit length (one meter) with a unit of bending moment divided by length unit [Nm/m]. The stiffness of one element \(C_i\) has a bending moment unit divided by length unit squared [Nm/m2] and is then:
\[ C_i = \frac{C}{s_d} \]
For a better understanding of the stiffness values, see the document European Recommendations on the Stabilization of Steel Structures by Sandwich Panels.
Hidden finite elements and RBE3 provide lateral and torsional stiffness to member plate
Note that RBE3 are only interpolation links that do not provide any stiffness on their own.
Verification
A model providing LTR was verified by LTBeam software, which uses bar (1D) elements with seven degrees of freedom. That means the cross-section is not deformed, but the element can capture warping. The comparison is shown on an example of IPE 180 cross-section from steel grade S355 with a length of 6 m. The beam is fixed at both ends with a uniform load of 20 kN/m applied at the top flange. Software LTBeam is able to determine the elastic critical moment that corresponds to the result of linear buckling analysis (LBA) in IDEA StatiCa Member.
Comparison of LTBeam and IDEA StatiCa Member for lateral and torsional stiffness
The critical load multiplier to elastic buckling \(\alpha_{cr}\) with lateral stiffness is very similar according to both software. The limit lateral stiffness where lateral-torsional buckling has an effect up to only 5 % of beam bending resistance is calculated according to EN 1993-1-1 as Slim = 8 589 kN. However, the results with torsional restraint are diverging at higher levels of rotational stiffness. Observing the deformed shape in IDEA StatiCa Member, the difference is caused by the cross-section deformation that can be captured only by the shell model. LTBeam provides unrealistically high critical load multipliers for high torsional stiffness.
To verify this claim, the ABAQUS shell element model was created at ETH university. The beam is again fixed on both ends, made of steel grade S355 and with a length of 6 m. Beam cross-section IPE 240 was used. Limit torsional stiffness, i.e. lateral-torsional buckling has an effect up to only 5 % of beam bending resistance, was calculated as Clim = 27.13 kNm/m. The model is loaded by force in the mid-span at the top flange.
Comparison of ABAQUS, LTBeam, and IDEA StatiCa Member for torsional stiffness
The effect of torsional stiffness is very similar in both models made of shell elements and LTBeam diverges. Most importantly, ABAQUS and IDEA StatiCa Member buckling resistances provided by GMNIA almost coincide – the differences are up to 4 %.
Stiffness estimation
LTR provided by floors filled with concrete and with composite action provided by shear studs may be assumed as rigid at least in the case of lateral stiffness. The stiffnesses provided by trapezoidal sheets of sandwich panels are much smaller and may be determined by experiments or calculations. Most often, the values of lateral and torsional stiffness would be recommended by manufacturers of sandwich panels or other types of cladding.
The calculation of lateral stiffness S [N] provided by trapezoidal sheets is provided in EN 1993-1-3, Chapter 10:
\[S=1000 \sqrt{t^3} \left ( 50+10 \sqrt[3]{b_{roof}} \right ) \frac{s}{h_w} \]
where:
- t – design thickness of trapezoidal sheeting [mm]
- broof – roof width, i.e. for gable roof it is the distance between a ridge and an eave [mm]
- s – distance between beams [mm]
- hw – trapezoidal sheet profile depth [mm]
The formula is valid if the trapezoidal sheet is connected to the beam at each rib. If the sheeting is connected to the beam at every second rib only, then S should be substituted by 0.2 S.
Lateral stiffness of sandwich panels is described in ECCS recommendation. The stiffness of fasteners is essential:
\[S=\frac{k_v}{2B} \sum_{k=1}^{n_k}c_k^2\]
where:
- kv – shear stiffness of a fastening
- B – width of a sandwich panel
- nk – number of pairs of fasteners per panel and support
- ck – distance between the two fasteners of a pair
Torsional stiffness is more complicated and can also be estimated by ECCS recommendation. It contains the contribution of fasteners, sandwich panel, and beam distortion. The beam distortion may be neglected because it is already included in the shell element model.
Torsional (on the left) and lateral stiffness (on the right) provided by sandwich panels (ECCS, 2014)
In American practice, restraint against lateral torsional buckling is typically assumed to be full or negligible based on the type and orientation of decking. For example, Table 8.1 of the AISC Seismic Design Manual identifies restraint conditions for beams subject to axial compression. However, where necessary, the lateral stiffness can be derived from the diaphragm stiffness, G’, computed in accordance with AISI S310. Denavit et al. (2020) present a method of calculating torsional stiffness.
References
- CTICM, LTBeam v. 1.0.11, available at: https://www.cesdb.com/ltbeam.html
- Abaqus. Reference manual, version 6.16. Simulia, Dassault Systéms. France, 2016.
- EN 1993-1-3: Eurocode 3: Design of steel structures – Part 1-3: General rules – Supplementary rules for cold-formed members and sheeting, CEN, 2006.
- ECCS TC7 – Technical Working Group TWG 7.9 Sandwich Panels and Related Structures, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2nd edition, 2014. ISBN 978-90-6363-081-2
- Denavit, M.D.; Jacobs, W.P.; Helwig, T.A. (2020). "Continuous Bracing Requirements for Constrained-Axis Torsional Buckling," Engineering Journal, American Institute of Steel Construction, Vol. 57, pp. 69-89.