This verification example was prepared by Mark D. Denavit and Kayla Truman-Jarrell in a joint project of The University of Tennessee and IDEA StatiCa.
1 Description
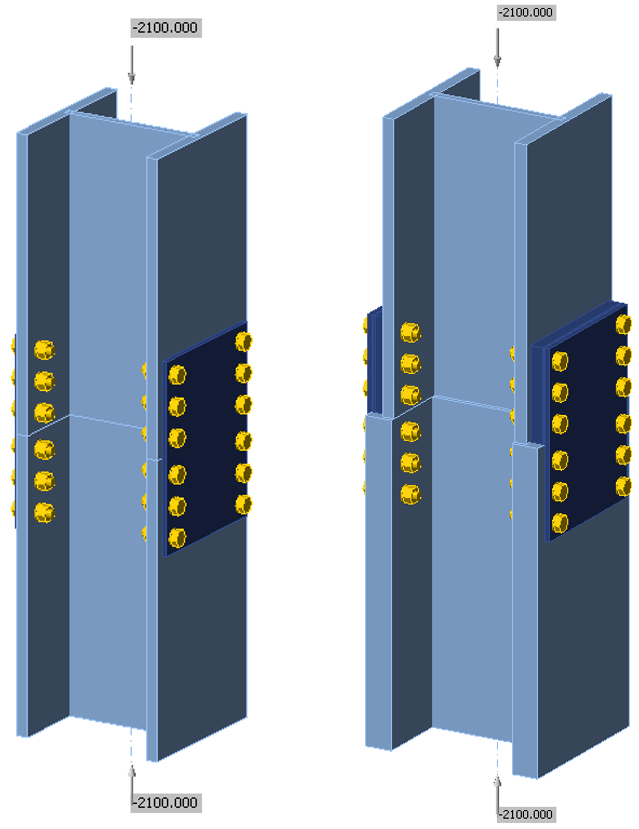
A comparison between results from the component-based finite element method (CBFEM) and traditional calculation methods used in US practice for bolted wide flange splice connections (Fig. 1) is presented in this study.
Fig. 1 Schematic of the bolted wide flange splice connection investigated in this study
The traditional calculation methods used in this work are based upon the requirements for load and resistance factor design (LRFD) in the AISC Specification (2016). The limit states evaluated in the traditional calculations include shear rupture, bearing, and tearout for the strength of the bolts; tensile yielding, tensile rupture, block shear rupture, and compression yielding for the strength of the splice plates; and tensile yielding, tensile rupture, compression yielding, and flexural yielding for the wide flange members. Deformation at the bolt hole at service load was assumed to be a design consideration. Slip was evaluated for some connections.
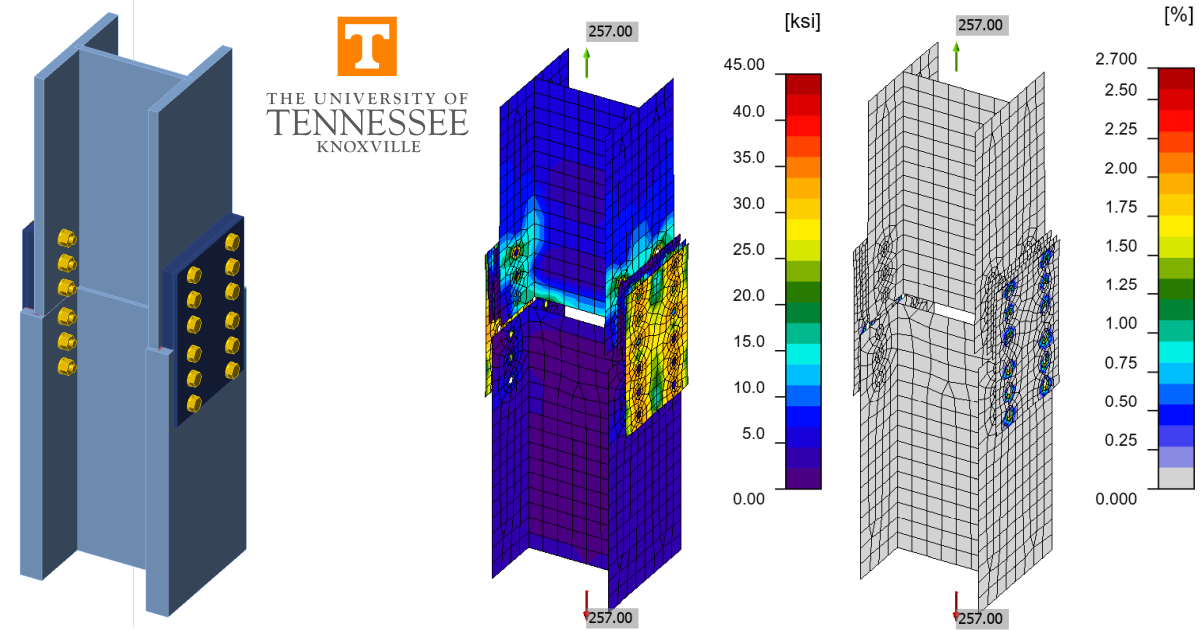
The CBFEM results were obtained from IDEA StatiCa Version 22.1. Example models are shown in Fig. 2. The maximum permitted loads were determined iteratively by adjusting the applied load input to a value that the program deems safe but if increased by a small amount (e.g., 1 kip) the program would deem unsafe.
Fig. 2 Bolted wide flange splice connections modeled in IDEA StatiCa.
For the comparisons presented in this study, the upper column was always a W14×159 and the lower column was either a W14×159 or W14×370. All wide flange shapes were assumed to conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The splice connection was based on Table 14-3 of the AISC Manual (2017). A total of 24, 7/8 in. diameter A490 bolts (threads not excluded from shear planes) were used in the connection (6 for each of the splice plate to column flange connections). The connection was not slip-critical, unless noted otherwise. There was no gap between the columns. The connections were evaluated both with consideration of contact bearing (Muir 2015) and also neglecting contact bearing. The bolt spacing was s = 3 in. and the vertical edge distances were lev1 = 1.5 in. and lev2 = 1.75 in., for a total length of 18.5 in. for the splice plate. The splice plate was 14 in. wide. The bolt gage was g = 11.5 in., and the horizontal edge distance was leh = 1.25 in. for some cases as recommended by Table 14-3. In other cases, the bolt gage was g = 8 in., and the horizontal edge distance was leh = 3 in. to avoid block shear rupture. The thickness of the splice plate varied in the analysis. Table 14-3 recommends a plate thickness of 0.5 in. for W14×159 columns. The splice plates were assumed to conform to ASTM A36 (Fy = 36 ksi, Fu = 58 ksi).
This column splice design is most appropriate for connecting two axially loaded columns through contact bearing. This study investigates cases where contact bearing is neglected, as well as cases where the columns are loaded in tension or with combined major-axis flexure. The same splice connection was used throughout the study for uniformity and ease of comparison; however, different connections would likely be more efficient for cases with significant tension or combined flexure.
2 Axial Loading
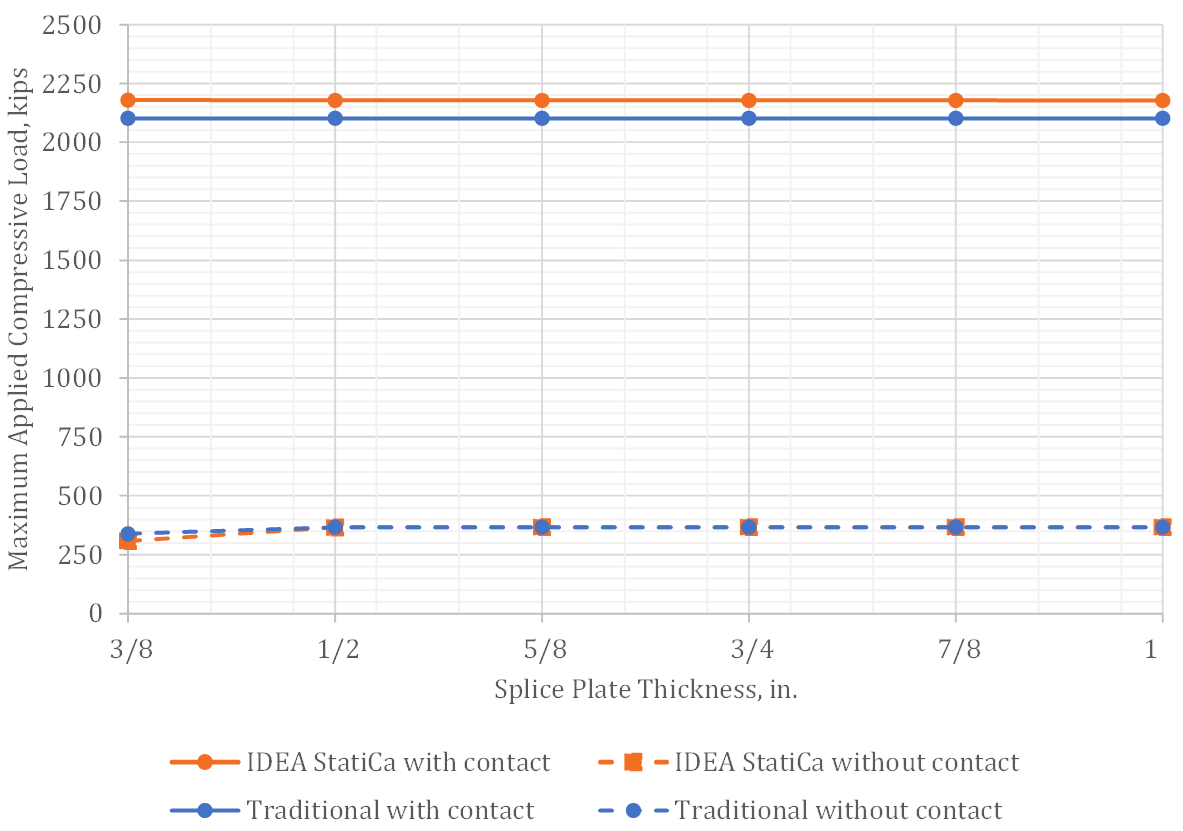
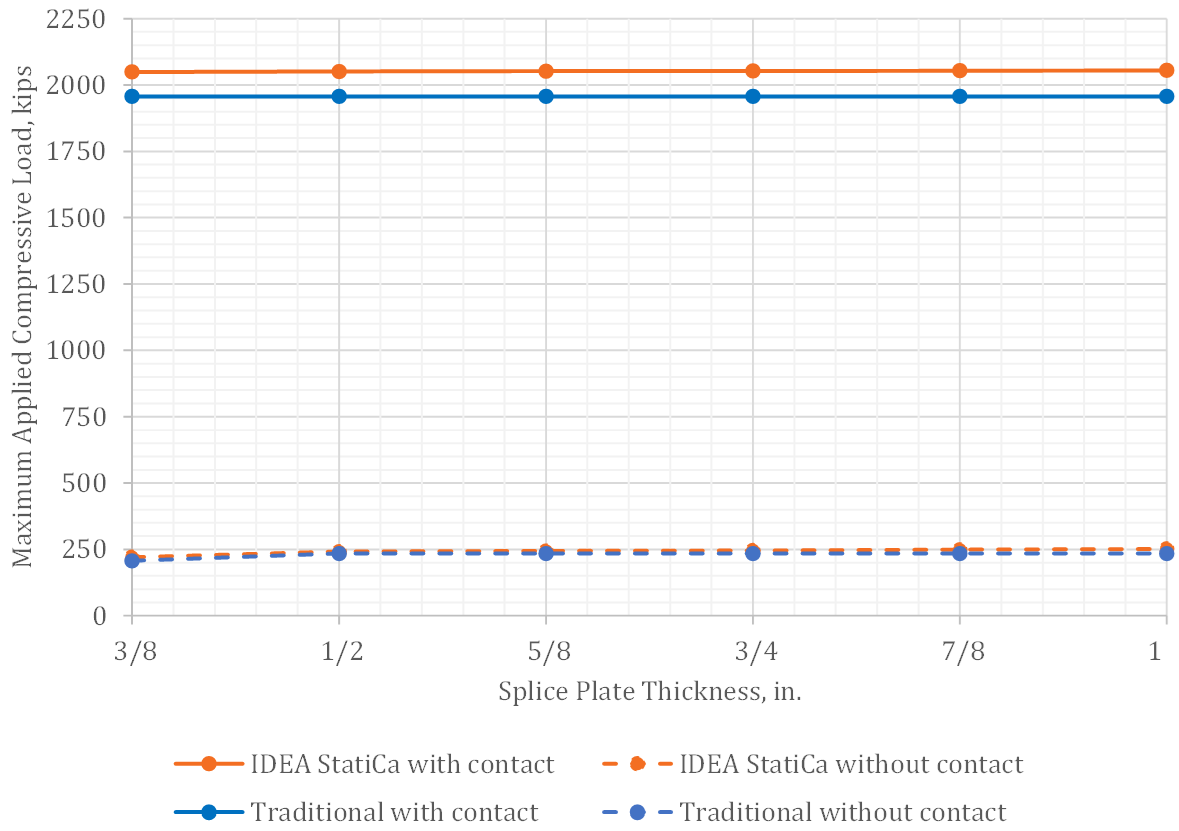
First, the strength of the connection under axial loading was investigated for the case of equal depth columns and bolt gage, g = 11.5 in. Variation of the maximum applied axial compression load with splice plate thickness is presented in Fig. 3. The strength of the connection is much greater with contact bearing than without. With contact bearing, the plastic strain limit in the column web controlled for IDEA StatiCa and compression yielding of the column controlled for the traditional calculations. The bolts and splice plates are essentially unstressed in these analyses; hence strength did not vary with splice plate thickness. IDEA StatiCa gives a maximum permitted load that is approximately 4% greater than the traditional calculations, primarily due to the small amount of strain hardening assumed in the model and small differences in the cross-sectional area of the wide flange (i.e., IDEA StatiCa does not model the fillets and a portion of the area at each junction of the web and flange is double counted).
Without contact bearing the load is transferred from one wide flange to the other through the bolts and splice plates. For the thinnest splice plate (i.e., 3/8 in.), the plastic strain limit in the splice plate controlled for IDEA StatiCa and compression yielding of the splice plate controlled for the traditional calculations. Note that Lc/r ≤ 25 for the splice plate when the effective length factor is taken as 0.65 for a fixed-fixed condition, so no stability reduction was applied. The maximum applied load was 309 kips for IDEA StatiCa and 340 kips for the traditional calculations. IDEA StatiCa gives a smaller maximum applied load because the stress in the splice plate is concentrated near the bolt holes. For all other splice plate thicknesses, bolt shear rupture controlled for both IDEA StatiCa and the traditional calculations, and the maximum applied load was identical.
Fig. 3 Maximum applied compressive load vs. splice plate thickness
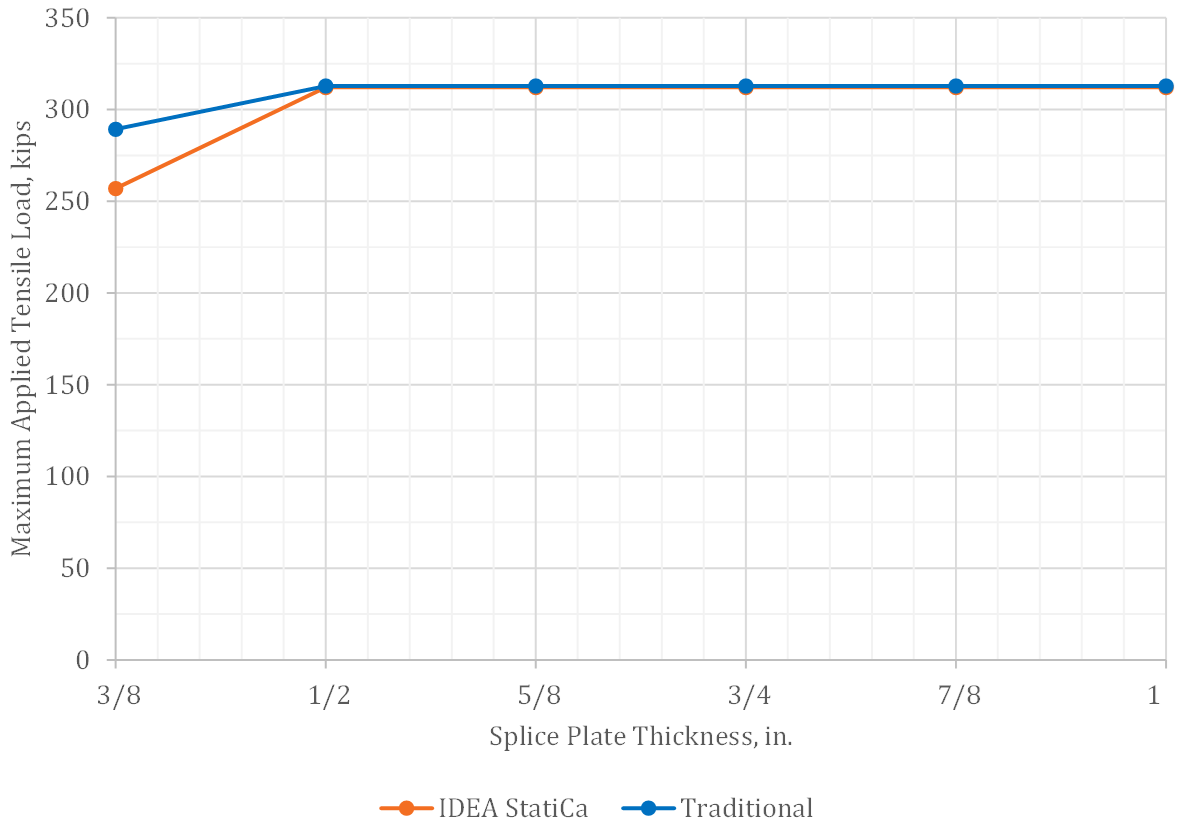
Variation of the maximum applied axial tensile load with splice plate thickness is presented in Fig. 4. The IDEA StatiCa analyses were performed with and without bearing contact operations, however, the results from the two cases were identical. The contact stiffness in tension is negligible.
For the connections with thicker splice plates (5/8 in. thick or more), bolt shear rupture controlled for both IDEA StatiCa and the traditional calculations. The maximum applied load was the same for the two methods. For the connections with thinner splice plates, tearout controlled the strength per IDEA StatiCa and block shear rupture of the splice plate controlled the strength per the traditional calculations. The mismatch in controlling limit states is resolved by refining the mesh in IDEA StatiCa. For the connection with 1/2 in. thick splice plates and the default mesh (maximum mesh size of 1.969 in.), tearout controls with a maximum applied tensile load of 341 kips. For a maximum mesh size of 1 in., the plastic strain limit is reached in the splice plates at an applied load of 338 kips. Further refinement to a maximum mesh size of 0.25 in., yields a maximum applied load of 328 kips with plastic strain of the splice plates controlling. The pattern of plastic strain for this connection is consistent with a block shear rupture failure (Fig. 5). Even with the refined mesh, IDEA StatiCa gives a greater maximum applied load than the traditional calculations. For the connection with 1/2 in. thick splice plates, the maximum applied load per the traditional calculations is 308 kips.
Researchers have noted that the block shear rupture provisions in the AISC Specification (2016) can be conservative in comparison to physical test data and have proposed alternative equations to better predict block shear rupture strength (Teh and Deierlein 2017). Their proposed equation for the nominal strength for block shear rupture, Rn = FuAnt + 0.6FuAev, utilizes and effective shear area, Aev, equal to the average of the gross and net shear areas currently used in the AISC Specification (i.e., Aev = (Agv + Anv)/2). The available strength for block shear rupture for the connection with 1/2 in. thick splice plates using this equation is 391 kips, thus other limit states would control. If the equation proposed by Teh and Deierlein (2017) is accurate, then the IDEA StatiCa results would be conservative.
Fig. 4 Maximum applied tensile load vs. splice plate thickness
Fig. 5 Plastic strain in splice plate at 328 kips applied load for connection with 1/2 in. thick splice plate and maximum mesh size of 0.25 in.
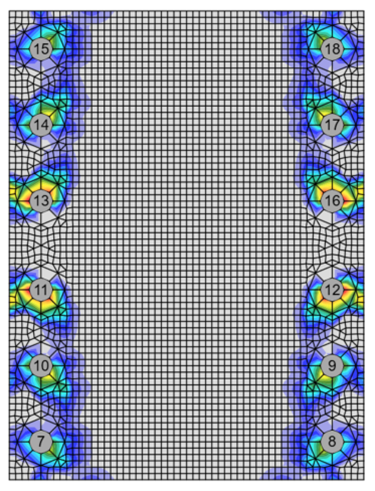
To further explore the behavior of this connection under tensile load, the analysis was re-run using a bolt gage of g = 8 in. Block shear rupture does not control the tensile strength of the splice plate with this value of g. Variation of the maximum applied axial tensile load with splice plate thickness for this case is presented in Fig. 6. The IDEA StatiCa results are essentially the same as for the case with the larger bolt gage. For IDEA StatiCa and the connections with the two thinnest splice plates (i.e., 3/8 in. and 1/2 in.), the controlling limit state was tearout with only the bolts at the extreme ends of the splice reaching 100% utilization (Fig. 7). Bolt shear rupture controlled for the other connections in IDEA StatiCa with all bolts reaching 100% utilization. For the traditional calculations, the strength of the bolt group controlled for all cases. However, the maximum applied load for the traditional calculations was greater than IDEA StatiCa for the connections with the two thinnest splice plates. For the traditional calculations, the effective strength of each bolt in the group is evaluated and summed to obtain the strength of the bolt group. Therefore, some of the bolts are controlled by tearout while others are controlled by shear rupture, but they all contribute their peak strength to the bolt group. In IDEA StatiCa, the bolts are all modeled with the same stiffness, so they all experience roughly the same load in this connection. For the thinner plates, tearout controls the strength of the extreme bolts and they achieve their strength first before the remaining bolts can achieve their strength. This is akin to the poison bolt method, which is more commonly used for eccentrically loaded bolt groups in traditional calculations. Using the poison bolt method in this case yields strength results more like those from IDEA StatiCa.
Fig. 6 Maximum applied tensile load vs. splice plate thickness (bolt gage, g = 8 in.)
Fig. 7 Display indicating bolt utilization at 256 kips applied load for connection with 3/8 in. thick splice plate
3 Axial Loading with Unequal Column Depths
When the columns to be connected have different depths, filler plates are used to pack out the depth of the smaller column and create a flush surface for the splice plates. Filler plates can be developed or undeveloped. Developed filler plates have additional attachment to the column beyond the splice plates. Undeveloped filler plates do not have additional attachment. The AISC Specification (2016) requires reductions in shear and slip strength for bolted connections with undeveloped fillers.
The results presented in this section are for a splice connection with a W14×159 upper column and W14×370 lower column. The difference in depth between these two shapes is 2.90 in., therefore it was assumed that the total thickness of filler plates was 1.45 in., which was achieved with two plies, one 1-1/4 in. thick and another 3/16 in. thick.
Variation of the maximum applied axial compression load with splice plate thickness is presented in Fig. 8. The bolt gage was taken as g = 11.5 in. for this case as would be typical for a column splice. With contact bearing, the results are essentially the same as for the case with equal depth columns and no fillers. Note, however, that contact was defined both between the upper wide flange and the lower wide flange and between the filler plates and the lower wide flange. If contact was defined only between the two wide flange members, the offset of flange centerlines resulted in bending of the flange (Fig. 9) and somewhat reduced strengths in IDEA StatiCa (1879 kips without contact of the filler plates versus 2121 kips with contact of the filler plates for the connection with 1/2 in. thick splice plates). Full-contact bearing is achieved since the two columns are of the same family (i.e., W14) and the distance between flanges is the same, so the traditional calculations are unaffected.
Without contact bearing, the strength of the splice is much less and IDEA StatiCa shows the exact same strength as the traditional calculations for all but the connection with the thinnest splice plates (i.e., 3/8 in. thick). Note that the reduction in shear strength for fillers defined in Section J5.2 of the AISC Specification (2016) is applied in both IDEA StatiCa and the traditional calculations. For the connection with the thinnest splice plates, the plastic strain in the splice plates controls in IDEA StatiCa resulting in a lower strength than the traditional calculations.
Fig. 8 Maximum applied compressive load vs. splice plate thickness for connections with filler plates
Fig. 9 Plastic strain results at 1920 kips applied load for connection with 1/2 in. thick splice plate and no contact between the filler plates and the lower wide flange (deformation scale factor = 10)
Variation of the maximum applied axial tension load with splice plate thickness is presented in Fig. 10. The bolt gage was taken as g = 8 in. for this case to avoid the block shear rupture limit state. As with the compression case, IDEA StatiCa and the traditional calculations give the same strength for all but the connection with the thinnest splice plates. For the connection with the thinnest splice plates, tearout controls some of the bolts and a difference in strength arises because of the different ways that IDEA StatiCa and the traditional calculations handle bolt groups with bolts of different strength.
A strength reduction also applies to the slip limit state for connections with two or more fillers between connected parts. The reduction is defined by hf, a factor for fillers, in Equation J3-4 of the AISC Specification (2016); hf = 0.85 for cases with two or more fillers between connected parts and hf = 1.0 otherwise. If the splice connection was slip-critical, the available strength would be 199 kips for the case of no fillers or single-ply fillers and 169 kips for the case of multi-ply fillers. Without contact bearing and defining the connection as slip-critical, the maximum applied axial load in tension per IDEA StatiCa is 152 kips for the connection with fillers and 1/2 in. thick splice plates. IDEA StatiCa detects the multiple fillers and applies the appropriate factor for fillers. The lower strength from IDEA StatiCa is because IDEA StatiCa considers the eccentric loading of the filler plates, which is resisted by a couple formed by contact pressure and bolt tension (Fig. 11). IDEA StatiCa conservatively neglects the friction due to the contact pressure while accounting for the applied tension in the bolt using the reduction factor ksc. (AISC Specification (2016) Section J3.9).
Fig. 10 Maximum applied tensile load vs. splice plate thickness for connections with filler plates
Fig. 11 Stress in contacts and bolt force results at 152 kips applied tensile load for connection with 1/2 in. thick splice plate and friction (slip-critical) bolts (deformation scale factor = 10)
4 Combined Axial and Major-Axis Flexure Loading
Splice connections may need to support more than just axial loads. For the case of 1000 kip-in. of major-axis bending moment applied concurrently with the axial load, the variation of the maximum applied compression load with splice plate thickness is presented in Fig. 12 and the variation of the maximum applied tensile load with splice plate thickness is presented in Fig. 13. The bolt gage was taken as g = 8 in. for analyses in this section to avoid the block shear rupture limit state.
In compression and with bearing contact, member strength controlled both the IDEA StatiCa analyses and the traditional calculations. Both maximum applied loads are reduced from the case with pure compression (Fig. 3) because of the concurrent bending moment. In compression without bearing contact and in tension, IDEA StatiCa gives slightly greater maximum applied loads than the traditional calculations for the connections with thicker splice plates where bolt shear rupture controls. In contrast, the IDEA StatiCa and the traditional calculations gave the same strength under concentric load. For the traditional calculations, the force in each bolt group was determined as P/2 ± M/d where d is the depth of the wide flange (Tamboli 2016). This equation assumes that shear in the bolts is the only force at the faying surface between the column flange and the splice plate. With explicit modeling of the connection in IDEA StatiCa, contact stress is observed at the faying surfaces (Fig. 14) which does not directly increase capacity (since friction at contact surfaces is neglected in IDEA StatiCa) but shifts the lever arm resisting the moment outward and reduces the shear in the bolts.
Fig. 12 Maximum applied compressive load vs. splice plate thickness for connection with concurrent major-axis flexure
Fig. 13 Maximum applied tensile load vs. splice plate thickness for connection with concurrent major-axis flexure
Fig. 14 Stress in contacts at 212 kips applied tensile load and 1000 kip-in applied major-axis moment for connection with 1/2 in. thick splice plate (deformation scale factor = 10)
Variation of maximum applied axial load with applied major-axis moment for the connection with 1/2 in. thick splice plates, no bearing contact, and bolt gage g = 8 in. is shown in Fig. 15. These results confirm that IDEA StatiCa matches well with the traditional calculations over the entire range of applied axial load and bending moment for this connection.
Fig. 15 Maximum applied axial load vs. applied major-axis moment (compression negative)
5 Summary
This study compared the design of bolted wide flange splice connections using traditional calculation methods used in US practice and IDEA StatiCa. Key observations from the study include:
- The available strength obtained from IDEA StatiCa agrees well with the traditional calculations.
- Among the greatest differences in strength were for connections where tearout controlled the strength of some bolts. IDEA StatiCa reached 100% utilization of the bolts controlled by tearout while other bolts did not reach 100% utilization, resulting in conservative comparisons to the traditional calculations which allow the strength of all bolts in a concentrically loaded bolt group to be obtained simultaneously.
- IDEA StatiCa gives somewhat higher strengths than the traditional calculations when block shear rupture controls.
- IDEA StatiCa correctly identified all connections in this study with undeveloped filler plates and subsequently applied the appropriate bolt shear or slip strength reductions defined in the AISC Specification (2016). However, the algorithm in IDEA StatiCa for identifying undeveloped filler plates does not cover all cases and engineering judgment is required in non-standard cases to ensure that the strength results are applied when appropriate.
6 References
AISC. (2016). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2017). Steel Construction Manual, 15th Edition. American Institute of Steel Construction, Chicago, Illinois.
Muir, L. (2015). “Bear It and Grin.” Modern Steel Construction, (December).
Tamboli, A. (2016). Handbook of Structural Steel Connection Design and Details, Third Edition. McGraw Hill, New York, NY.
Teh, L. H., and Deierlein, G. G. (2017). “Effective Shear Plane Model for Tearout and Block Shear Failure of Bolted Connections.” Engineering Journal, AISC, 54(3), 181–194.