Calculation assumptions
The behavior of a reinforced concrete section subjected to torsion can be divided into two categories - before and after the time when the cracks may first be expected to occur. Before a crack the cross-section behaves as an elastic material. Torsion stress can be expressed by formula
\[\tau =~\frac{{{T}_{Ed}}}{{{W}_{t}}}\]
where Wt je sectional module in torsion.
Cracks in the unreinforced member due to principal tensile torsion stress are also ultimate limit state. The behavior of a reinforced concrete section subjected to torsion can be described on the basis of a thin-walled closed section, see Fig. below.
\[ \textsf{\textit{\footnotesize{\qquad Equivalent thin-walled cross-section.}}}\]
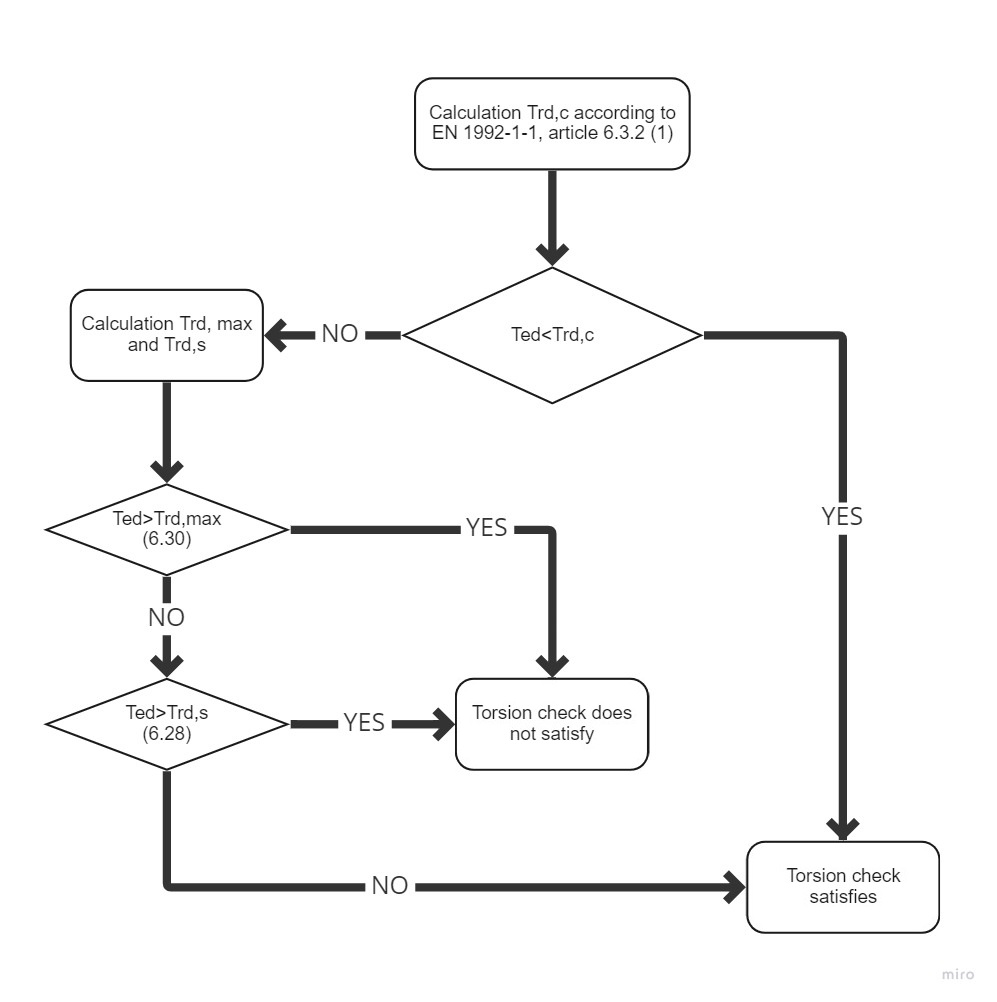
Calculation procedure
The process of a reinforced concrete check for torsion is very similar to the check for shear. First of all, we check the concrete resistance. If the concrete check is satisfied, the reinforcement can be designed using the detailing rules. Otherwise, we need to verify the reinforcement and compressive diagonal resistance by calculation.
\[ \textsf{\textit{\footnotesize{\qquad Process diagram for torsion check.}}}\]
Resistance
Shear flow in a wall of a thin-walled cross-section under torsion can be expressed as:
\[ {{\tau }_{t}}{{t}_{ef}}=~\frac{{{T}_{Ed}}}{2{{A}_{k}}}\]
Shear force in a wall of a thin-walled cross-section can be expressed as:
\[ V={{\tau }_{t}}{{t}_{ef}}z\]
Where
τ Shear flow in wall,
tef is the effective wall thickness,
z is the side length of wall,
TEd is the torsion moment,
Ak is the area enclosed by the center-lines of the connecting walls, including inner hollow areas.
Torsion cracking moment, which may be determined by setting fctd to previous expression. Thus we get expression for the resistance in torsion without torsion reinforcement.
\[ {{T}_{Rd,c}}=2{{A}_{k}}{{t}_{ef}}{{f}_{ctd}}\]
where fctd design axial tensile strength of concrete
\[ \textsf{\textit{\footnotesize{\qquad Principles of Truss analogy for member under torsion moment.}}}\]
The member resistance with torsion reinforcement is composed from the resistance of compressive concrete diagonals which is based again on the truss analogy method. Compressive stress in the diagonal can be expressed with help of shear force in the wall of a thin-walled cross-section on the wall surface which is in consideration, i.e.
\[{{\sigma }_{c}}=\frac{\frac{{{T}_{Ed}}z}{2{{A}_{k}}\sin \theta }}{z~{{t}_{ef}}\cos \theta }=\frac{{{T}_{Ed}}}{2{{A}_{k}}{{t}_{ef}}\sin \theta \cos \theta }\]
Substitution of σc=σcwfcd and TEd=TRd,max and expressing of TRd,max we get an equation for the compressive diagonal resistance
\[{{T}_{Rd,max}}=2~\nu ~{{\alpha }_{cw}}~{{f}_{cd}}~{{A}_{k}}~{{t}_{ef~\sin \theta ~\cos \theta }}\]
where
ν = 0,6 pro fck ≤ 60MPa or for fck > 60MPa
αcw coefficient which takes account the state of compressive stress in compression chord
fcd design value of concrete compressive strength
the shear reinforcement resistance subjected to torsion is again based on stress in the compression diagonal. The stirrup force is equal to the stress in the compressed diagonal on the area which corresponds to the particular stirrup line, i.e.
\[{{A}_{sw}}{{f}_{ywd}}=\frac{{{T}_{Ed}}}{2{{A}_{k}}{{t}_{ef}}\sin \theta \cos \theta }~{{t}_{ef}}~s{{\sin }^{2}}\theta =\frac{{{T}_{Ed}}~s}{2{{A}_{k}}\cot \theta }~\]
Substituting TEd=TRd,s and expressing TRd,s we get equation:
\[{{T}_{Rd,s}}=2{{A}_{k}}\frac{{{A}_{sw}}{{f}_{ywd}}}{s}~\cot \theta\]
If the longitudinal and shear reinforcement quantity is known, we can define angle θ by the expression
\[{{\tan }^{2}}\theta =\frac{\frac{{{A}_{sw}}{{f}_{ywd}}}{s}}{\frac{{{A}_{sl}}{{f}_{yd}}}{{{u}_{k}}}}\]
Substitution for TRd,s we get
\[{{T}_{Rd,s}}=2{{A}_{k}}\sqrt{\frac{{{A}_{sw}}}{s}{{f}_{ywd~}}\frac{{{A}_{sl}}}{{{u}_{k}}}~{{f}_{yd}}}\]
Where
Asw shear reinforcement area
s is the radial spacing of stirrups of shear reinforcement
fywd is the effective design strength of the shear reinforcement
Asl longitudinal reinforcement area
uk is the outer circumference of the cross-section
fywd is the effective design strength of the longitudinal reinforcement
The force in the longitudinal reinforcement can be deducted from The shear force in a wall of a section subject to a pure torsional moment, which is give as:
\[V=\frac{{{T}_{Ed}}}{2{{A}_{k}}}{{u}_{k}}\]
That force is transformed to longitudinal direction and we get:
\[{{F}_{l}}=\frac{{{T}_{Ed}}{{u}_{k}}}{2{{A}_{k}}~\tan \theta }\]
The permitted range of the values for angle θ is similar to the shear check, i.e 1 < cot θ < 2,5. Dependency between resistances can be seen in Fig. below. The diagram shows that with increasing the angle θ the resistance TRd,max is growing, the resistance TRd.s is decreasing and resistance TRd,c is constant, since it is not based on the truss analogy method.
\[ \textsf{\textit{\footnotesize{\qquad Závislost únosnosti průřezu v kroucení na úhlu θ.}}}\]
Calculation of cross-section characteristics for torsion
To check the cross-section for torsion it is necessary to establish a so-called equivalent thin-walled closed section. In determining the dimensions of the equivalent thin-walled cross-section by assuming a rectangular shape. For the true area of rectangular states A = b×h and for the circumference of rectangle u =2 (b +h). Using these two equations can provide alternative thin rectangle-shaped area and periphery of the original cross-section. Solving two equations with two unknowns we get:
\[b=\frac{-u\pm \sqrt{{{u}^{2}}-16A}}{-4}\text{ }\!\!~\!\!\text{ }\]
\[h=\frac{\left( u-2\text{b} \right)}{2}\]
The wall thickness of the effective cross-section can be define from periphery and section area as:
\[t=\text{A}/\text{u}\]
Then the area and periphery defined by center line of the effective cross-section:
\[{{A}_{k}}=\left( \text{h}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\]
\[{{u}_{k}}=2\left( \left( \text{h}-\text{t} \right)+\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right) \right)\]
The problem with this method is for cross-section of type T with a wide plate when the overall area and periphery is taken to calculate the dimensions (including this plate). In the future versions of IDEA RCS program, the selection of the most massive cross-section part will be enabled, which will be used to check the torsion.