Pressupostos de cálculo
O comportamento de uma secção de betão armado sujeita a torção pode ser dividido em duas categorias - antes e depois do momento em que se espera que as fissuras ocorram pela primeira vez. Antes de uma fissura, a secção transversal comporta-se como um material elástico. A tensão de torção pode ser expressa pela fórmula
\[\tau =~\frac{{{T}_{Ed}}}{{{W}_{t}}}\]
onde Wt je módulo seccional em torção.
As fendas na barra não reforçada devido à tensão de torção principal são também o estado limite último. O comportamento de uma secção de betão armado sujeita a torção pode ser descrito com base numa secção fechada de parede fina, ver Fig. abaixo.
\[ \textsf{\textit{\footnotesize{\qquad Secção de parede fina equivalente.}}}\]
Procedimento de cálculo
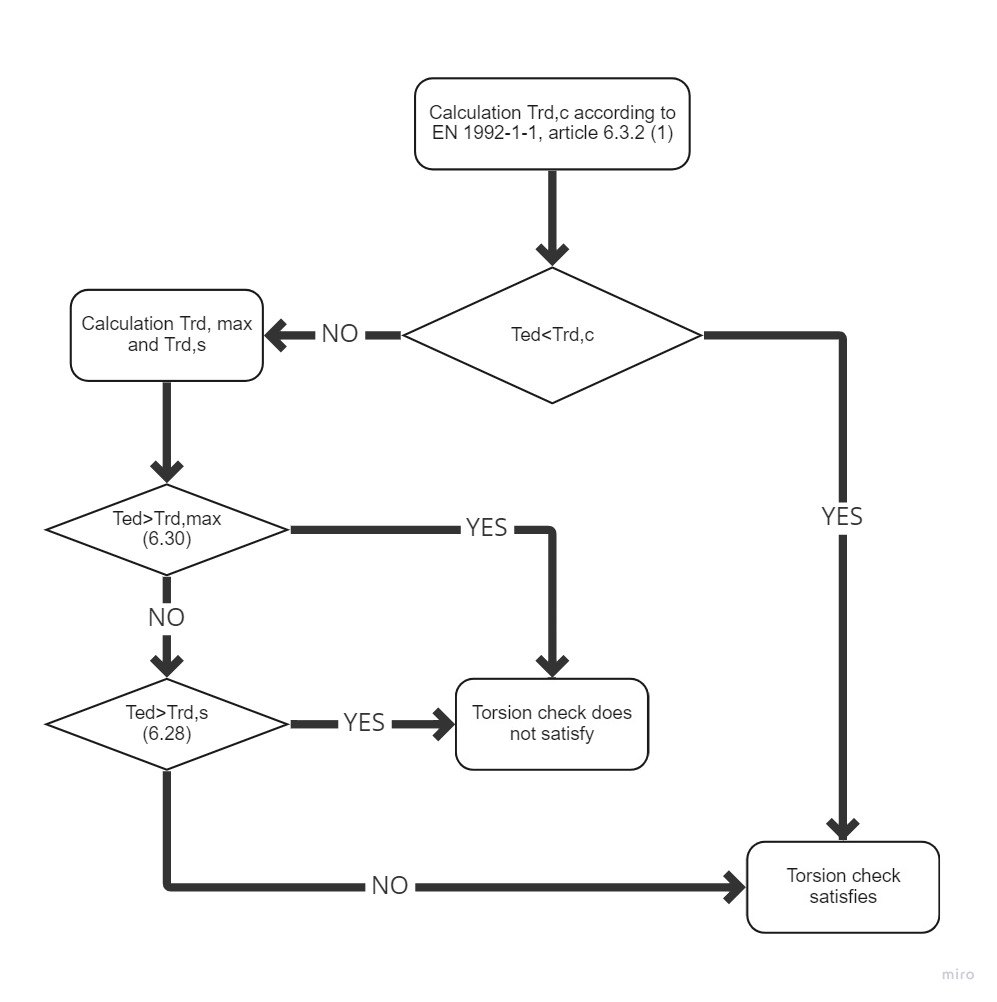
O processo de uma verificação de betão armado para torção é muito semelhante à verificação para corte. Em primeiro lugar, verificamos a resistência do betão.Se a verificação do betão for satisfeita, a armadura pode ser dimensionada utilizando as regras de pormenorização. Caso contrário, é necessário verificar a armadura e a resistência diagonal à compressão através do cálculo.
\[ \textsf{\textit{\footnotesize{\qquad Diagrama de processo para verificação de torção.}}}\]
Resistência
O fluxo de corte numa parede de uma secção de parede fina sob torção pode ser expresso como:
\[ {{\tau }_{t}}{{t}_{ef}}=~\frac{{{T}_{Ed}}}}{2{{A}_{k}}}\]
A força de corte numa parede de uma secção transversal de parede fina pode ser expressa como:
\[ V={{\tau }_{t}}{{{t}_{ef}}z\]
Onde
τ Fluxo de cisalhamento na parede,
tef é a espessura efectiva da parede,
z é o comprimento lateral da parede,
TEd é o momento de torção,
Ak é a área delimitada pelas linhas centrais das paredes de ligação, incluindo as áreas ocas interiores.
Momento de torção de fendilhação, que pode ser determinado ajustando fctd à expressão anterior. Assim, obtém-se a expressão para a resistência à torção sem armadura de torção.
\[ {{T}_{Rd,c}}=2{{A}_{k}}{{t}_{ef}}{{f}_{ctd}}\]
onde fctd resistência à tração axial de projeto do betão
\[ \textsf{\textit{\footnotesize{\qquad Principles of Truss analogia para membro sob momento de torção.}}}\]
A resistência da barra com armadura de torção é composta a partir da resistência das diagonais de betão à compressão, que se baseia novamente no método de analogia de treliça. A tensão de compressão na diagonal pode ser expressa com a ajuda da força de corte na parede de uma secção de parede fina na superfície da parede que está em consideração, ou seja
\[{{\sigma }_{c}}=\frac{\frac{{{T}_{Ed}}z}{2{{A}_{k}}\sin \theta }}{z~{{t}_{ef}}\cos \theta }=\frac{{{T}_{Ed}}}{2{{A}_{k}}{{{t}_{ef}}\sin \theta \cos \theta }\]
Substituindo σc=σcwfcd eTEd=TRd,max e expressandoTRd,max obtemos uma equação para a resistência diagonal à compressão
\[{{T}_{Rd,max}}=2~\nu ~{{\alpha }_{cw}}~{{f}_{cd}}~{{A}_{k}}~{{t}_{ef~\sin \theta ~\cos \theta }}\]
em que
ν = 0,6 para fck ≤ 60MPa ou para fck > 60MPa
Coeficiente αcw que tem em conta o estado de tensão de compressão na corda de compressão
fcd valor de projeto da resistência à compressão do betão
a resistência da armadura de corte sujeita a torção é novamente baseada na tensão na diagonal de compressão. A força do estribo é igual à tensão na diagonal comprimida na área que corresponde à linha de estribo específica, ou seja
\[{{A}_{sw}}{{f}_{ywd}}=\frac{{{T}_{Ed}}}}{2{{A}_{k}}{{{t}_{ef}}\sin \theta \cos \theta }~{{t}_{ef}}~s{\sin }^{2}}\theta =\frac{{{T}_{Ed}}}~s}{2{{A}_{k}}\cot \theta }~\]
SubstituindoTEd=TRd,s e exprimindoTRd, s obtemos a equação:
\[{{T}_{Rd,s}}=2{{A}_{k}}\frac{{{A}_{sw}}{{f}_{ywd}}}{s}~\cot \theta\]
Se a quantidade de armadura longitudinal e de corte for conhecida, podemos definir o ângulo θ através da expressão
\[{{\tan }^{2}}\theta =\frac{\frac{{{A}_{sw}}{{f}_{ywd}}}{s}}{\frac{{{A}_{sl}}{{f}_{yd}}}{{{u}_{k}}}}\]
Substituindo porTRd,s obtemos
\[{{T}_{Rd,s}}=2{{A}_{k}}\sqrt{\frac{{{A}_{sw}}}{s}{{f}_{ywd~}}\frac{{{A}_{sl}}}{{{u}_{k}}}~{{f}_{yd}}}\]
Onde
Asw área de armadura de corte
s é o espaçamento radial dos estribos da armadura de cisalhamento
fywd é a resistência efectiva de projeto da armadura de corte
Asl área da armadura longitudinal
uk é o perímetro exterior da secção transversal
fywd é a resistência efectiva de projeto da armadura longitudinal
A força na armadura longitudinal pode ser deduzida da força de corte numa parede de uma secção sujeita a um momento de torção puro, que é dada como
\[V=\frac{{{T}_{Ed}}}{2{{A}_{k}}}{{u}_{k}}\]
Essa força é transformada para a direção longitudinal e obtemos:
\[{{F}_{l}}=\frac{{{T}_{Ed}}{{u}_{k}}}{2{{A}_{k}}~\tan \theta }\]
O intervalo permitido dos valores para o ângulo θ é semelhante ao da verificação de cisalhamento, ou seja, 1 < cot θ < 2,5. A dependência entre as resistências pode ser vista na Fig. abaixo. O diagrama mostra que com o aumento do ângulo θ a resistênciaTRd,max está a aumentar, a resistênciaTRd.s está a diminuir e a resistênciaTRd,c é constante, uma vez que não se baseia no método de analogia de treliça.
\[ \textsf{\textit{\footnotesize{\qquad Závislost únosnosti průřezu v kroucení na úhlu θ.}}}\]
Cálculo das caraterísticas da secção transversal para torção
Para verificar a secção transversal para torção, é necessário estabelecer uma chamada secção fechada de parede fina equivalente. Para determinar as dimensões da secção transversal de parede fina equivalente, assumindo uma forma retangular.Para a área real dos estados rectangulares A = b×h e para a circunferência do retângulo u =2 (b +h).A utilização destas duas equações pode fornecer uma área alternativa em forma de retângulo fino e a periferia da secção transversal original. Resolvendo duas equações com duas incógnitas, obtemos
\[b=\frac{-u\pm \sqrt{{{u}^{2}}-16A}}{-4}\text{ }\!\!~\!\!\text{ }\]
\[h=\frac{\left( u-2\text{b} \right)}{2}\]
A espessura da parede da secção transversal efectiva pode ser definida a partir da periferia e da área da secção como:
\[t=\text{A}/\text{u}\]
Em seguida, a área e a periferia definidas pela linha central da secção efetiva:
\[{{A}_{k}}=\left( \text{h}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right)\text{ }\!\!~\!\!\text{ }\]
\[{{u}_{k}}=2\left( \left( \text{h}-\text{t} \right)+\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right) \right)\]
O problema com este método é para secções transversais do tipo T com uma placa larga quando a área total e a periferia são consideradas para calcular as dimensões (incluindo esta placa).Nas versões futuras do programa IDEA RCS, será permitida a seleção da parte da secção mais maciça, que será utilizada para verificar a torção.