Main assumptions and limitations for CSFM
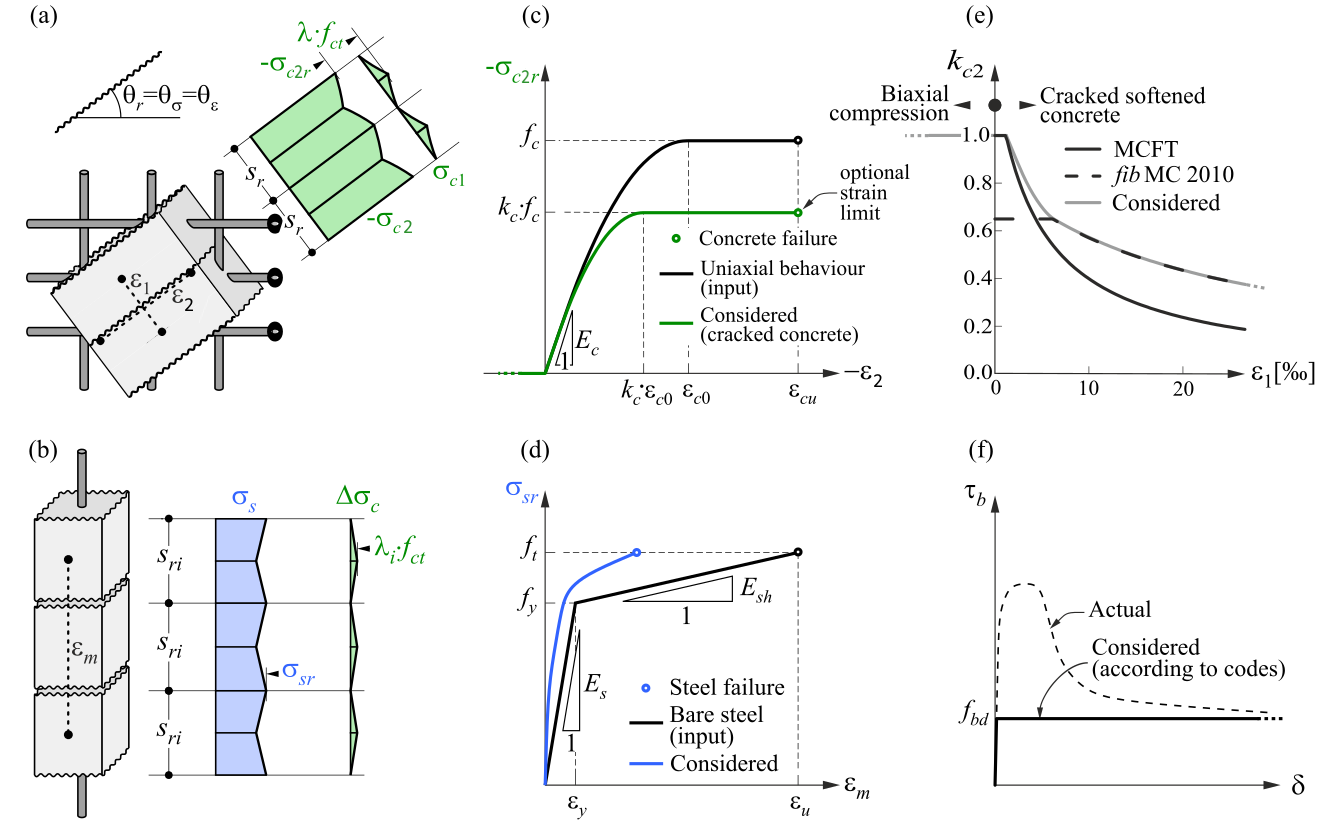
CSFM considers maximum principal concrete stress in compression (σc2r) and reinforcement stresses (σsr) at the cracks while neglecting the concrete tensile strength (σc1r = 0), except for its stiffening effect on the reinforcement. The consideration of tension stiffening allows the average reinforcement strains (εm) to be simulated. Fictitious, rotating, stress-free cracks that open without slip (Fig. 2a) are considered and the equilibrium at the cracks together with the average strains of the reinforcement is also taken into account.
\( \textsf{\textit{\footnotesize{Fig. 2\qquad Basic assumptions of the CSFM: (a) principal stresses in concrete; (b) stresses in the reinforcement direction;}}}\) \( \textsf{\textit{\footnotesize{(c) stress-strain diagram of concrete in terms of maximum stresses with consideration of compression softening;}}}\) \( \textsf{\textit{\footnotesize{(d) stress-strain diagram of reinforcement in terms of stresses at cracks and average strains; (e) compression softening}}}\) \( \textsf{\textit{\footnotesize{law; (f) bond shear stress-slip relationship for anchorage length verifications.}}}\)
Despite their simplicity, similar assumptions have been demonstrated to yield accurate predictions for reinforced members subjected to in-plane loading (Kaufmann 1998; Kaufmann and Marti 1998) if the provided reinforcement avoids brittle failures at cracking. Furthermore, the non-consideration of any contribution of the tensile strength of concrete to the ultimate load is consistent with the principles of modern design codes, which are mostly based on plasticity theory.
However, the CSFM is not suited for slender elements without transverse reinforcement since relevant mechanisms for such elements as aggregate interlock, residual tensile stresses at the crack tip, and dowel action – all of them relying directly or indirectly on the tensile strength of the concrete – are disregarded. While some design standards allow the design of such elements based on semi-empirical provisions, the CSFM is not intended for this type of potentially brittle structure.
Concrete
The concrete model implemented in the CSFM is based on the uniaxial compression constitutive laws prescribed by design codes for the design of cross-sections, which only depend on compressive strength. The parabola-rectangle diagram (Fig. 2c) is used by default in the CSFM, but designers can also choose a more simplified elastic ideal plastic relationship. When assessing according to the ACI code, it is possible to use only the parabola-rectangle stress-strain diagram. As previously mentioned, the tensile strength is neglected, as it is in classic reinforced concrete design.
The effective compressive strength is automatically evaluated for cracked concrete based on the principal tensile strain (ε1) by means of the kc2 reduction factor, as shown in Fig. 2c and e. The implemented reduction relationship (Fig. 2e) is a generalization of the fib Model Code 2010 proposal for shear verifications, which contains a limiting value of 0.65 for the maximum ratio of effective concrete strength to concrete compressive strength, which is not applicable to other loading cases.
The CSFM in IDEA StatiCa Detail does not consider an explicit failure criterion in terms of strains for concrete in compression (i.e., it considers an infinitely plastic branch after the peak stress is reached). This simplification does not allow the deformation capacity of structures failing in compression to be verified. However, their ultimate capacity is properly predicted when, in addition to the factor of cracked concrete (kc2) defined in (Fig. 2e), the increase in the brittleness of concrete as its strength rises is considered by means of the \( \eta_{fc} \) reduction factor defined in fib Model Code 2010 as follows:
\[f_{c,red} = k_c \cdot f_{c} = \eta _{fc} \cdot k_{c2} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
where:
kc is the global reduction factor of the compressive strength
kc2 is the reduction factor due to the presence of transverse cracking
fc is the concrete cylinder characteristic strength (in MPa for the definition of \( \eta_{fc} \)).
There is also a reduction of the kc2 factor because of the stability of the calculation. This reduction doesn't influence the total strength of members. Assuming fcd value as the factored strength of concrete (design value), the kc2 value is reduced according to the following rules.
σc2r < 0.11fcd kc2=1.0
0.11fcd < σc2r < 0.37fcd kc2 is a linear interpolation between 1.0 and the value taken from the
graph displayed in Fig. 2f
σc2r > 0.37fcd kc2 is directly taken from the graph from Fig. 2f
Reinforcement
The idealized bilinear stress-strain diagram for the bare reinforcing bars typically defined by design codes (Fig. 2d) is considered. The definition of this diagram only requires the basic properties of the reinforcement to be known during the design phase (strength and ductility class). A user-defined stress-strain relationship can also be defined.
Tension stiffening is accounted for by modifying the input stress-strain relationship of the bare reinforcing bar in order to capture the average stiffness of the bars embedded in the concrete (εm).
Bond model
Bond-slip between reinforcement and concrete is introduced in the finite element model by considering the simplified rigid-perfectly plastic constitutive relationship presented in Fig. 2f, with fbd being the design value (factored value) of the ultimate bond stress specified by the design code for the specific bond conditions.
This is a simplified model with the sole purpose of verifying bond prescriptions according to design codes (i.e., anchorage of reinforcement). The reduction of the anchorage length when using hooks, loops, and similar bar shapes can be considered by defining a certain capacity at the end of the reinforcement, as will be described further.