Check of steel connection components (AISC)
CBFEM method combines the advantages of the general Finite Element Method and standard Component Method. The stresses and internal forces calculated on the accurate CBFEM model are used in checks of all components.
Individual components are checked according to the American Institute of Steel Construction (AISC) 360-16.
Code-check of steel plates (AISC)
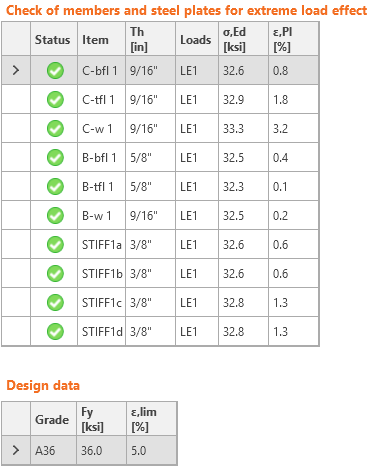
The resulting equivalent stress (HMH, von Mises) and plastic strain are calculated on plates. When the yield strength (in LRFD multiplied by material resistance factor ϕ = 0.9, in ASD divided by material safety factor Ω = 1.67, which are editable in Code setup) on the bilinear material diagram is reached, the check of the equivalent plastic strain is performed. The limit value of 5 % is suggested in Eurocode (EN1993-1-5 App. C, Par. C8, Note 1). This value can be modified in the Code setup, but verification studies were made for this recommended value.
The plate element is divided into five layers, and elastic/plastic behavior is investigated in each of them. The program shows the worst result of all of them.
The CBFEM method can provide stress a little bit higher than yield strength. The reason is the slight inclination of the plastic branch of the stress-strain diagram, which is used in the analysis to improve the stability of the interaction calculation. This is not a problem for practical design. The equivalent plastic strain is exceeded at higher stress, and the joint does not satisfy anyway.
Code-check of welds (AISC)
Fillet welds are checked according to AISC 360 - Chapter J2. The strength of CJP groove welds is assumed the same as the base metal and is not checked.
Fillet welds
The design strength, ϕRn, and the allowable strength, Rn/Ω, of welded joints are evaluated in the connection weld check.
ϕ = 0.75 (Load and Resistance Factor Design, LRFD, editable in Code setup)
Ω = 2.00 (Allowable Strength Design, ASD, editable in Code setup)
Available strength of welded joints is evaluated according to AISC 360-16 – J2.4
Rn = Fnw Awe
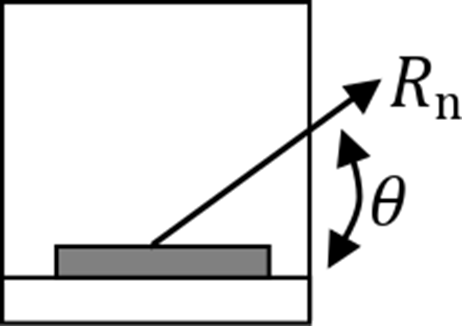
Fnw = 0.6 FEXX (1.0 + 0.5 sin1.5θ )
where:
- Fnw – nominal stress of weld material
- Awe – effective area of the weld
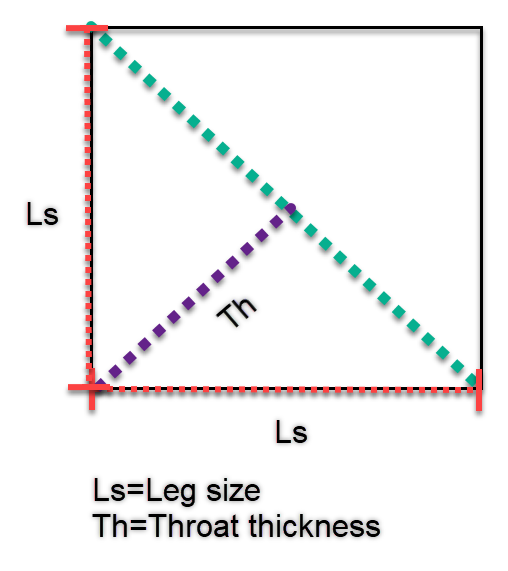
- Awe = Lc*Th
- FEXX – electrode classification number, i.e., minimum specified tensile strength
- θ – angle calculated between the longitudinal axis of the weld and resultant force direction acting in the most stressed finite element of the weld.
Note that directional strength increase is not used for welds where the edge of a rectangular hollow structural section is connected (AISC 360-16:2022 – J2.4.(2).
Base metal strength is evaluated if the option is selected in Code setup (Base metal capacity at the fusion face).
Rn = FnBM ABM – AISC 360-16 – J2.4 (J2-2)
where:
- FnBM = 0.6 Fu – nominal strength of the base metal – AISC 360-16 – J4.2 (J4-4)
- \( A_{BM}=A_{we}\sqrt{2} \) – cross-sectional area of the base metal
- Fu – specified minimum tensile strength
All values required for check are printed in tables.
where:
- Xu – used welding electrode
- Th – weld throat thickness (calculated from Ls)
- Ls – weld leg size (user input)
- \(L\) – total weld length
- \(L_c\) – length of critical weld element
- Loads – critical load effect for investigated weld
- \(F_n\) – force in critical weld element
- \(\phi\)Rn – weld resistance
- Ut – utilization of the critical weld element
The force, \(F_n\), and weld angle, \(\theta\), are derived from stresses \( \sigma_{\perp}, ,\ \tau_{\perp}, \, \tau_{\parallel}\), length and effective area of weld finite element. These stresses are the basic output of finite element solver.
The weld diagrams show stress according to the following formulas:
If base metal is deactivated (matching electrode is used):
\[ \sigma = \frac{\sqrt{ \sigma_{\perp}^2 + \tau_{\perp}^2 + \tau_{\parallel}^2 }}{1+0.5 \sin^{1.5}{\theta}} \]
If base metal is activated (matching electrode is not used):
\[ \sigma = \max \left \{ \frac{\sqrt{ \sigma_{\perp}^2 + \tau_{\perp}^2 + \tau_{\parallel}^2 }}{1+0.5 \sin^{1.5}{\theta}}, \, \frac{\sqrt{ \sigma_{\perp}^2 + \tau_{\perp}^2 + \tau_{\parallel}^2 }}{\sqrt{2} F_u / F_{EXX}} \right \} \]
User Note: In IDEA StatiCa, when weld leg size is input as 0, the following value is used:
- For single-sided fillet weld, weld throat thickness equals the thinner connected plate.
- For double-sided fillet weld, weld throat thickness equals half of the thinner connected plate.
CJP groove welds
AISC Specification Table J2.5 identifies four loading conditions that might be associated with groove welds and shows that the strength of the joint is either controlled by the base metal or that the loads need not be considered in the design of the welds connecting the parts. Accordingly, when Complete Joint Penetration (CJP) groove welds are made with matching-strength filler metal, the strength of a connection is governed or controlled by the base metal and no checks on the weld strength are required.
PJP groove welds
The design strength, ϕRn, and the allowable strength, Rn/Ω, of PJP groove weld is determined according to AISC 360-22 – Table J2.5). The most conservative case – load type by shear – is assumed.
ϕ = 0.75 (Load and Resistance Factor Design, LRFD, editable in Code setup)
Ω = 2.00 (Allowable Strength Design, ASD, editable in Code setup)
Available strength of welded joints is evaluated according to AISC 360-16 – J2.4
Rn = Fnw Awe
where:
- Fnw = 0.6 FEXX – nominal stress of weld material
- Awe – effective area of the weld
- Awe = Lc E
- FEXX – electrode classification number, i.e., minimum specified tensile strength
- Lc – length of critical weld element
- E – effective throat of PJP weld
Base metal strength is evaluated if the option is selected in Code setup (Base metal capacity at the fusion face).
Rn = FnBM ABM – AISC 360-22 – J2.4 (J4)
where:
- FnBM = 0.6 Fu – nominal strength of the base metal – AISC 360-22 – J4.2 (J4-4)
- \( A_{BM}=A_{we} \) – cross-sectional area of the base metal assumed to be equal to the effective area of the weld
- Fu – specified minimum tensile strength of base metal
Code-check of bolts and preloaded bolts (AISC)
The forces in bolts are determined by finite element analysis. The tensile forces include prying forces. The bolt resistances are checked according to AISC 360 - Chapter J3.
Bolts
Tensile and shear strength of bolts
The design tensile or shear strength, ϕRn, and the allowable tensile or shear strength, Rn/Ω of a snug-tightened bolt is determined according to the limit states of tension rupture and shear rupture as follows:
Rn = FnAb
ϕ = 0.75 (LRFD, editable in Code setup)
Ω = 2.00 (ASD, editable in Code setup)
where:
Ab – nominal unthreaded body area of bolt or threaded part
Fn – nominal tensile stress, Fnt, or shear stress, Fnv, from Table J3.2
The required tensile strength includes any tension resulting from prying action produced by the deformation of the connected parts.
Combined Tension and shear in bearing type connection
The available tensile strength of a bolt subjected to combined tension and shear is determined according to the limit states of tension and shear rupture as follows:
Rn = F'nt Ab (AISC 360-16 J3-2)
ϕ = 0.75 (LRFD, editable in Code setup)
Ω = 2.00 (ASD, editable in Code setup)
\( F'_{nt}=1.3 F_{nt} - \frac{f_{rv} F_{nt}}{\phi F_{nv}} \) (AISC 360-16 J3-3a LRFD)
\( F'_{nt}=1.3 F_{nt} - \frac{f_{rv} \Omega F_{nt}}{F_{nv}} \) (AISC 360-16 J3-3b ASD)
where:
- F'nt – nominal tensile stress modified to include the effects of shear stress
- Fnt – nominal tensile stress from AISC 360-16 Table J3.2
- Fnv – nominal shear stress from AISC 360-16 Table J3.2
- frv – required shear stress using LRFD or ASD load combinations. The available shear stress of the fastener shall be equal or exceed the required shear stress, frv
Bearing strength in bolt holes
The available bearing strengths, ϕRn and Rn/Ω, at bolt holes are determined for the limit state of bearing as follows:
ϕ = 0.75 (LRFD, editable in Code setup)
Ω = 2.00 (ASD, editable in Code setup)
The nominal bearing strength of the connected material, Rn, is determined as follows:
For a bolt in a connection with standard holes:
Rn = 1.2 lc t Fu ≤ 2.4 d t Fu (AISC 360-16 J3-6a, J3-6a, c)
For a bolt in a connection with slotted holes:
Rn = 1.0 lc t Fu ≤ 2.0 d t Fu (AISC 360-16 J3-6a, J3-6e, f)
where:
- Fu – specified minimum tensile strength of the connected material
- d – nominal bolt diameter
- lc – clear distance, in the direction of the force, between the edge of the hole and the edge of the adjacent hole or edge of the material
- t – thickness of the connected material
Preloaded bolts
The design slip resistance of preloaded class A325 or A490 bolt with the effect of tensile force Ft
Preloading force to be used AISC 360-10 tab. J3.1.
Tb = 0.7 fub As
Design slip resistance per bolt AISC 360-10 par. J3.8
Rn = kSC μ Du hf Tb ns
Utilization in shear [%]:
Uts = V / ϕRn (LRFD)
Uts = Ω V / Rn (ASD)
where:
- As – tensile stress area of the bolt
- fub – ultimate tensile strength
- \( k_{SC}=1-\frac{F_t}{D_u T_b n_b} \) – factor for combined tension and shear (LRFD) (J3-5a)
- \( k_{SC}=1-\frac{1.5 F_t}{D_u T_b n_b} \) – factor for combined tension and shear (ASD) (J3-5b)
- μ – mean slip factor coefficient editable in Code setup
- Du = 1.13 – multiplier that reflects the ratio of the mean installed bolt pretension to the specified minimum bolt pretension
- hf = 1.0 – factor for fillers
- ns – number of the friction surfaces; Check is calculated for each friction surface separately
- V – shear force acting on the bolt
- ϕ = 1.0 – resistance factor for standard size holes (LRFD) editable in Code setup
- ϕ = 0.7 – resistance factor for slotted holes (LRFD)
- Ω = 1.5 – resistance factor for standard size holes (ASD) editable in Code setup
- Ω = 2.14 – resistance factor for slotted holes (ASD)
Code-check of concrete blocks (AISC)
Concrete below base plate is simulated by the Winkler subsoil with uniform stiffness, which provides the contact stresses. The average stress at the loaded area in contact with the base plate is used for compressive check.
Concrete in compression
Concrete design bearing strength in compression is designed according to AISC 360-16, Section J8. When the supporting surface of the concrete is larger than the base plate, the design bearing strength is defined as
\[ f_{p(max)}=0.85 f_c \sqrt{\frac{A_2}{A_1}} \le 1.7 f'_c \]
where:
- f'c – concrete compressive strength
- A1 – base plate area in contact with a concrete surface (upper surface area of the frustum)
- A2 – concrete supporting surface (geometrically similar lower area of the frustum having its slopes of 1 vertical to 2 horizontal)
The assessment of concrete in the bearing is as follows
σ ≤ ϕc fp(max) for LRFD
σ ≤ fp(max) / Ωc for ASD
where:
- σ – average compressive stress under the base plate
- ϕc = 0.65 – resistance factor for concrete
- Ωc = 2.31 – safety factor for concrete
Transfer of shear forces
Shear loads can be transferred via one of these options:
- Shear lug,
- Friction,
- Anchor bolts.
Shear lug
Only LFRD is available. The shear load is transferred via the shear lug. The concrete in bearing and, unless reinforcement is provided to develop the required strength, concrete breakout checks are necessary.
The bearing capacity of shear lug against concrete is determined according to ACI 349-01 – B.4.5 and ACI 349-01 RB11 as:
ϕPbr = ϕ 1.3 f'c A1 + ϕ Kc (Ny – Pa)
where:
- ϕ = 0.7 – strength reduction factor for bearing on concrete according to ACI 349
- f'c – concrete compressive strength
- A1 – projected area of the embedded shear lug in the direction of the force, excluding the portion of the lug in contact with the grout above concrete member
- Kc = 1.6 – confinement coefficient
- Ny = n Ase Fy – yield strength of tensioned anchors
- Pa – external axial load
The concrete breakout strength of the shear lug according to ACI 349 – B11 is:
\[ \phi V_{cb} = A_{Vc} 4 \phi \sqrt{f'_c} \]
where:
- ϕ = 0.85 – strength reduction factor for shear according to ACI 349
- AVc – effective stress area defined by projecting a 45° plane from the bearing edges of the shear lug to the free surface in the direction of the shear load. The bearing area of the shear lug is excluded from the projected area
If the concrete breakout resistance in Code setup is disabled, user is provided with the force that needs to be transferred via reinforced concrete.
Friction
The shear load is transferred via friction. The shear resistance is determined as:
ϕc Vr = ϕc μ C (LRFD)
Vr / Ωc =μ C / Ωc (ASD)
where:
- ϕc = 0.65 – resistance factor (LRFD)
- Ωc = 2.31 – safety factor (ASD)
- μ = 0.4 – coefficient of friction between base plate and concrete (recommended value 0.4 in AISC Design guide 7 – 9.2 and ACI 349 – B.6.1.4, editable in Code setup)
- C – compressive force
Anchor bolts
If the shear load is transferred via anchor bolts only, the shear force acting on each anchor is determined by FEA and anchor bolts are assessed according to ACI 318-14 as described in the following chapters.
Code-check of anchors (AISC)
The forces in anchors including prying forces are determined by finite element analysis, but the resistances are checked using code provisions of ACI 318-14 - Chapter 17.
Only LFRD is available. Anchor rods are designed according to AISC 360-16 – J9 and ACI 318-14 – Chapter 17. The following resistances of anchor bolts are evaluated:
- Steel strength of anchor in tension ϕNsa,
- Concrete breakout strength in tension ϕNcbg,
- Concrete pullout strength ϕNp,
- Concrete side-face blowout strength ϕNsb,
- Steel strength of anchor in shear ϕVsa,
- Concrete breakout strength in shear ϕVcbg,
- Concrete pryout strength of anchor in shear ϕVcp.
The user must choose the concrete condition (cracked or non-cracked – with no cracks in service condition) and the type of anchors (with or without washer plates).
Following checks of anchors loaded in tension are not provided and should be checked using information in relevant Technical Product Specification (based on the 5 percent fractile of tests performed and evaluated according to ACI 355.2):
- Pull-out failure of fastener (for post-installed mechanical anchors) – ACI 318-19: 17.6.3,
- Bond strength of adhesive anchor (for post-installed bonded anchors) – ACI 318-19: 17.6.5,
- Concrete splitting failure during installation should be evaluated by ACI 355.2 requirements.
Concrete blow-out failure is provided only for anchors with washer plates.
Steel strength of anchor in tension
Steel strength of anchor in tension is determined according to ACI 318-14 – 17.4.1 as
ϕNsa = ϕ Ase,N futa
where:
- ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, the factor is editable in Code setup
- Ase,N – tensile stress area
- futa – specified tensile strength of anchor steel and shall not be greater than 1.9 fya and 125 ksi
Concrete breakout strength
Concrete breakout strength is designed according to the Concrete Capacity Design (CCD) in ACI 318-14 – Chapter 17. In the CCD method, the concrete cone is considered to be formed at an angle of approximately 34° (1 vertical to 1.5 horizontal slope). For simplification, the cone is considered to be square rather than round in plan. The concrete breakout stress in the CCD method is considered to decrease with an increase in size of the breakout surface. Consequently, the increase in strength of the breakout in the CCD method is proportional to the embedment depth to the power of 1.5. Anchors whose concrete cones overlap create a group of anchors which create a common concrete cone. Note that no equivalent ASD solution exists for concrete capacity design.
\[ \phi N_{cbg} = \phi \frac{A_{Nc}}{A_{Nco}} \psi_{ec,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_b \]
where:
- ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, the factor is editable in Code setup
- ANc – actual concrete breakout cone area for a group of anchors that create a common concrete cone
- ANco = 9 hef2 – concrete breakout cone area for single anchor not influenced by edges
- \( \psi_{ec,N} = \frac{1}{1+\frac{2 e'_N}{3 h_{ef}}} \) – modification factor for anchor groups loaded eccentrically in tension; in the case where eccentric loading exists about two axes, the modification factor Ψec,N is calculated for each axis individually and the product of these factors is used
- \( \psi_{ed,N} = \min \left ( 0.7 + \frac{0.3 c_{a,min}}{1.5 h_{ef}}, 1 \right ) \) – modification factor for edge distance
- ca,min – smallest distance from the anchor to the edge
- Ψc,N – modification factor for concrete conditions; Ψc,N =1 for cracked concrete, Ψc,N =1.25 for non-cracked concrete
- Ψcp,N = min (ca,min / cac,1) – modification factor for splitting for post-installed anchors designed for uncracked concrete without supplementary reinforcement to control splitting; Ψcp,N = 1 for all other cases
- \( N_b = k_c \lambda_a \sqrt{f'_c} h_{ef}^{1.5} \) – basic concrete breakout strength of a single anchor in tension in cracked concrete; for cast-in anchors and 11 in. ≤ hef ≤ 25 in. \( N_b = 16 \lambda_a \sqrt{f'_c} h_{ef}^{5/3} \)
- kc = 24 for cast-in anchors
- hef – depth of embedment; according to Chapter 17.4.2.3 in ACI 318-14, the effective embedment depth hef is reduced to \( h_{ef} = \max \left ( \frac{c_{a,max}}{1.5}, \frac{s}{3} \right ) \) if anchors are located less than 1.5 hef from three or more edges
- s – spacing between anchors
- ca,max – maximum distance from an anchor to one of the three close edges
- λa = 1 – modification factor for lightweight concrete
- f'c – concrete compressive strength [psi]
According to ACI 318-14 – 17.4.2.8, in case of headed anchors, the projected surface area ANc is determined from the effective perimeter of the washer plate, which is the lesser value of da + 2 twp or dwp, where:
- da – anchor diameter
- dwp – washer plate diameter or edge size
- twp – washer plate thickness
The group of anchors is checked against the sum of tensile forces in anchors loaded in tension and creating a common concrete cone.
The concrete breakout cone area for group of anchors loaded by tension that create common concrete cone, Ac,N, is shown by red dashed line.
According to ACI 318-14 – 17.4.2.9, where anchor reinforcement is developed in accordance with ACI 318-14 – 25 on both sides of the breakout surface, the anchor reinforcement is presumed to transfer the tension forces, and concrete breakout strength is not evaluated.
Concrete pullout strength
Anchor bolts with washer plate (headed bolts):
Concrete pullout strength of a headed anchor bolt is defined in ACI 318-14 – 17.4.3 as
ϕNpn = ϕΨc,P Np
where:
- ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
- Ψc,P – modification factor for concrete condition; Ψc,P = 1.0 for cracked concrete, Ψc,P = 1.4 for non-cracked concrete
- NP = 8 Abrg f'c for headed anchor
- Abrg – bearing area of the head of stud or anchor bolt
- f'c – concrete compressive strength
Hooked anchor bolts (J- or L-bolts):
Concrete pullout strength of a hooked anchor bolt is defined in ACI 318-14 – 17.4.3 as
ϕNpn = ϕΨc,P Np
where:
- ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
- Ψc,P – modification factor for concrete condition; Ψc,P = 1.0 for cracked concrete, Ψc,P = 1.4 for non-cracked concrete
- NP = 0.9 f'c eh da for hooked anchor bolt
- f'c – concrete compressive strength
- eh – distance from the inner surface of the shaft of a J- or L-bolt to the outer tip of the J- or L-bolt
- da – anchor bolt diameter
Concrete pullout strength for other types of anchors than headed or hooked is not evaluated in the software and has to be specified by the manufacturer.
Concrete side-face blowout strength
Concrete side-face blowout strength of headed anchor in tension is defined in ACI 318-14 – 17.4.4 as
\[ \phi N_{sb} = \phi 160 c_{a1} \sqrt{A_{brg}} \sqrt{f'_c} \]
The concrete side-face blowout strength is multiplied by one of reduction factors:
- \( \frac{1+\frac{c_{a2}}{c_{a1}}}{4} \le 1 \)
- \( \frac{1+\frac{s}{6 c_{a1}}}{2} \le 1 \)
where:
- ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
- ca1 – shorter distance from the centreline of an anchor to an edge
- ca2 – longer distance, perpendicular to ca1, from the centreline of an anchor to an edge
- Abrg – bearing area of the head of stud or anchor bolt
- f'c – concrete compressive strength
- s – spacing between two adjacent anchors near one edge
Steel strength in shear
The steel strength in shear is determined according to ACI 318-14 – 17.5.1 as
ϕVsa = ϕ 0.6 Ase,V futa
where:
- ϕ = 0.65 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
- Ase,V – tensile stress area
- futa – specified tensile strength of anchor steel and shall not be greater than 1.9 fya and 125 ksi
If mortar joint is selected, steel strength in shear Vsa is multiplied by 0.8 (ACI 318-14 – 17.5.1.3).
The shear on lever arm, which is present in the case of base plate with oversized holes and washers or plates added to the top of the base plate to transmit the shear force, is not considered.
Concrete breakout strength of anchor in shear
The concrete breakout strength of an anchor or anchor group in shear is designed according to ACI 318 14 – 17.5.2.
\[ \phi V_{cbg} = \phi \frac{A_V}{A_{Vo}} \psi_{ec,V} \psi_{ed,V} \psi_{c,V} \psi_{h,V} \psi_{\alpha,V} V_b \]
where:
- ϕ = 0.65 – strength reduction factor for anchors in shear according to ACI 318-14 – 17.3.3, editable in Code setup
- Av – projected concrete failure area of an anchor or group of anchors
- Avo – projected concrete failure area of one anchor when not limited by corner influences, spacing, or member thickness
- \( \psi_{ec,V} = \frac{1}{1+\frac{2 e'_V}{3 c_{a1}}} \) – modification factor for anchor groups loaded eccentrically in shear
- \( \psi_{ed,V} = 0.7 + 0.3 \frac{c_{a2}}{1.5 c_{a1}} \le 1.0 \) – modification factor for edge effect
- Ψc,V – modification factor for concrete condition; Ψc,V = 1.0 for cracked concrete, Ψc,V = 1.4 for non-cracked concrete
- \( \psi_{h,V} = \sqrt{\frac{1.5 c_{a1}}{h_a}} \ge 1 \) – modification factor for anchors located in a concrete member where ha < 1.5 ca1
- \( \psi_{\alpha ,V} = \sqrt{\frac{1}{(\cos \alpha_V )^2 + (0.5 \sin \alpha_V)^2}} \) – modification factor for anchors loaded at an angle 90° − αV with the concrete edge; in ACI 318-14 – 17.5.2.1 are only discrete values, equation is taken from FIB bulletin 58 – Design of anchorages in concrete (2011)
- ha – height of a failure surface on the concrete side
- \( V_b = \min \left ( 7 \left ( \frac{l_e}{d_a} \right )^{0.2} \lambda_a \sqrt{d_a} \sqrt{f'_c} c_{a1}^{1.5}, 9 \lambda_a \sqrt{d_a} \sqrt{f'_c} c_{a1}^{1.5} \right ) \)
- le = hef ≤ 8 da – load-bearing length of the anchor in shear
- da – anchor diameter
- f'c – concrete compressive strength
- ca1 – edge distance in the direction of load; according to Cl. 17.5.2.4, for a narrow member, c2,max < 1.5 c1 that is also deemed to be thin, ha < 1.5 c1, c'1 is used in previous equations instead of c1; the reduced c'1 = max (c2,max / 1.5, ha / 1.5, sc,max / 3)
- ca2 – edge distance in the direction perpendicular to load
- c2,max – largest edge distance in the direction perpendicular to load
- sc,max – maximum spacing perpendicular to direction of shear, between anchors within a group
If ca2 ≤ 1.5 ca1 and ha ≤ 1.5 ca1, \( c_{a1}= \max \left ( \frac{c_{a2}}{1.5}, \frac{h_a}{1.5}, \frac{s}{3} \right ) \), where s is the maximum spacing perpendicular to direction of shear, between anchors within a group.
According to ACI 318-14 – 17-5.2.9, where anchor reinforcement is developed in accordance with ACI 318-14 – 25 on both sides of the breakout surface, the anchor reinforcement is presumed to transfer the shear forces and concrete breakout strength is not evaluated.
Concrete pryout strength of anchor in shear
Concrete pryout strength is designed according to ACI 318-14 – 17.5.3.
ϕVcp = ϕkcp Ncp
where:
- ϕ = 0.65 – strength reduction factor for anchors in shear according to ACI 318-14 – 17.3.3, editable in Code setup
- kcp = 1.0 for hef < 2.5 in., kcp = 2.0 for hef ≥ 2.5 in
- Ncp = Ncb (concrete breakout strength – all anchors are assumed in tension) in case of cast-in anchors
According to ACI 318-14 – 17.4.2.9, where anchor reinforcement is developed in accordance with ACI 318-14 – 25 on both sides of the breakout surface, the anchor reinforcement is presumed to transfer the tension forces, and concrete breakout strength is not evaluated.
Interaction of tensile and shear forces
Interaction of tensile and shear forces is assessed according to ACI 318-14 – R17.6.
\[ \left ( \frac{N_{ua}}{N_n} \right )^{\zeta} + \left ( \frac{V_{ua}}{V_n} \right )^{\zeta} \le 1.0 \]
where:
- Nua and Vua – design forces acting on an anchor
- Nn and Vn – the lowest design strengths determined from all appropriate failure modes
- ς = 5 / 3
Anchors with stand-off
The bar element is designed according to AISC 360-16. Interaction of shear force is neglected because the minimum length of the anchor to fit the nut under the base plate ensures that the anchor fails in bending before the shear force reaches half the shear resistance, and the shear interaction is negligible (up to 7 %). Interaction of bending moment and compressive or tensile force is conservatively assumed as linear. Second order effects are not taken into account.
Shear resistance (AISC 360-16 – G):
\( V_n = \frac{0.6 A_V F_y}{\Omega_V} \) (ASD)
\( V_n = \phi_V 0.6 A_V F_y \) (LRFD)
- AV = 0.844 ∙ As – the shear area
- As – bolt area reduced by threads
- Fy – bolt yield strength
- ΩV – safety factor, recommended value is 2
- ϕV – resistance factor, recommended value is 0.75
Tensile resistance (AISC 360-16 – D2):
\( P_n = \frac{A_s F_y}{\Omega_t} \) (ASD)
\( P_n = \phi_t A_s F_y \) (LRFD)
- Ωt – safety factor, recommended value is 2
- ϕt – resistance factor, recommended value is 0.75
Compressive resistance (AISC 360-16 – E3)
\( P_n = \frac{F_{cr} A_s}{\Omega_c} \) (ASD)
\( P_n = \phi_c F_{cr} A_s \) (LRFD)
- \( F_{cr} = 0.658^{\frac{F_y}{F_e}} F_y \) for \( \frac{L_c}{r} \le 4.74 \sqrt{\frac{E}{F_y}} \), \( F_{cr} = 0.877 F_e \) for \( \frac{L_c}{r} > 4.74 \sqrt{\frac{E}{F_y}} \) – critical stress
- \( F_e = \frac{\pi^2 E} {\left ( \frac{L_c}{r} \right) ^2} \) – elastic buckling stress
- Lc = 2 ∙ l – buckling length
- l – length of the bolt element equal to half the base plate thickness + gap + half the bolt diameter
- \( r= \sqrt{\frac{I}{A_s}} \) – radius of gyration of the anchor bolt
- \( I= \frac{\pi d_s^4}{64} \) – moment of inertia of the bolt
- Ωc – safety factor, recommended value is 2
- ϕc – resistance factor, recommended value is 0.75
Bending resistance (AISC 360-16 – F11):
\( M_n = \frac{Z F_y}{\Omega_b} \le \frac{1.6 S_x F_y}{\Omega_b} \) (ASD)
\( M_n = \phi_b Z F_y \le 1.6 \phi_b S_x F_y \) (ASD)
- \( Z = \frac{d_s^3}{6} \) – plastic section modulus of the bolt
- \( S_x= \frac{2 I}{d_s} \) – elastic section modulus of the bolt
- Ωc – safety factor, recommended value is 2
- ϕc – resistance factor, recommended value is 0.75
Linear interaction:
\[ \frac{N}{P_n}+\frac{M}{M_n} \le 1 \]
- N – the tensile (positive) or compressive (negative sign) factored force
- Pn – the tensile (positive) or compressive (negative sign) design or allowable strength
- M – the factored bending moment
- Mn – the design or allowable bending resistance
Detailing of bolts and welds (AISC)
Bolts
The minimum spacing between bolts and distance to the bolt centre to an edge of a connected part are checked. The minimum spacing 2.66 times (editable in Code setup) the nominal bolt diameter between centres of bolts is checked according to AISC 360-16 – J.3.3. The minimum distance to the bolt centre to an edge of a connected part is checked according to AISC 360-16 – J.3.4; the values are in Table J3.4 and J3.4M.
Welds
The minimal and maximal weld size and the sufficient length of the weld are checked.
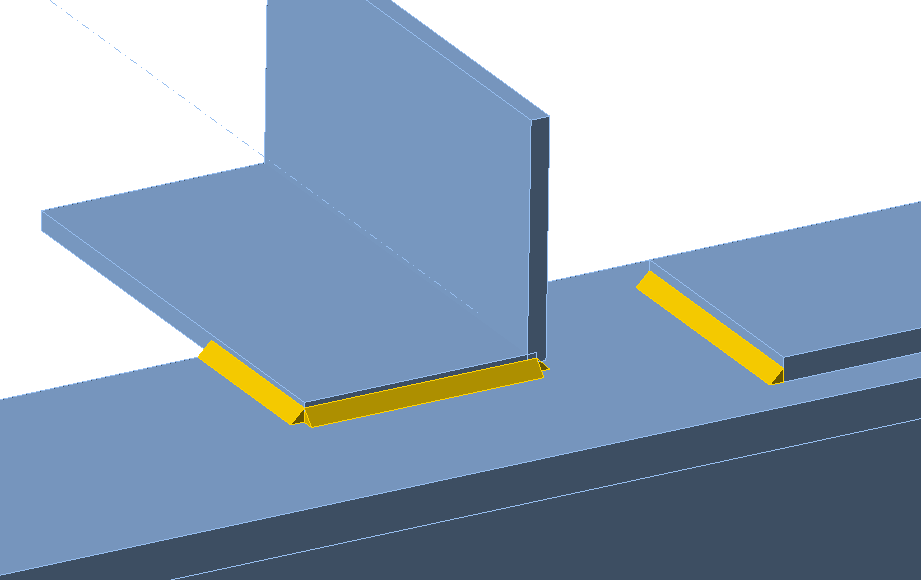
The maximal weld size is checked according to AISC 360-16 – J2.2b for a plate parallel to the welded plate with an edge-to-surface fillet weld.
- For plate thickness smaller than 1/4 in, the weld size should be no bigger than plate thickness.
- For plate thickness equal to or higher than 1/4 in, the weld size should be no bigger than the plate thickness −1/16 in.
Examples for welds where maximum thickness is checked are in the following figure.
The minimal weld size of fillet weld is checked according to Table J2.4:
- For \(t_p \le 1/4\,\textrm{in}\) the weld size should be higher than or equal to 1/8 in.
- For \(1/4\,\textrm{in}< t_p \le 1/2\,\textrm{in}\) the weld size should be higher than or equal to 3/16 in.
- For \(1/2\,\textrm{in}< t_p \le 3/4\,\textrm{in}\) the weld size should be higher than or equal to 1/4 in.
- For \(3/4\,\textrm{in}< t_p\) the weld size should be higher than or equal to 5/16 in.
where \(t_p\) is the thickness of the thinner plate.
The minimum length of fillet welds should not be less than four times the weld size according to J2.2b (c).
The minimal effective throat of PJP groove weld is determined according to AISC 360-22 – Table J2.3:
| Thickness of thinner part joint [in.] | Minimum effective throat [in.] |
| \(t_p \le 0.25\) | 0.1250 |
| \(0.25 < t_p \le 0.50\) | 0.1875 |
| \(0.50 < t_p \le 0.75\) | 0.2500 |
| \(0.75 < t_p \le 1.50\) | 0.3125 |
| \(1.50 < t_p \le 2.25\) | 0.3750 |
| \(2.25 < t_p \le 6\) | 0.5000 |
| \(6.00 < t_p\) | 0.6250 |
Anchors
The spacing between anchors should be greater than four times anchor diameter according to ACI 318-14 – 17.7.1.
Minimum plate edge distance follows rules for bolts.
Steel joint classification (AISC)
Joints are classified according to joint stiffness to:
- Rigid – joints with insignificant change of original angles between members,
- Semirigid – joints which are assumed to have the capacity to furnish a dependable and known degree of flexural restraint,
- Simple – joints which do not develop bending moments.
Joints are classified according to the commentary in AISC 360-16, Cl. B3.4.
- Rigid – \( \frac{S_{j,ini} L_b}{E I_b} \ge 20 \)
- Semirigid – \( 2 < \frac{S_{j,ini} L_b}{E I_b} < 20 \)
- Simple – \( \frac{S_{j,ini} L_b}{E I_b} \le 2 \)
where:
- Sj,ini – initial stiffness of the joint; the joint stiffness is assumed linear up to the 2/3 of Mj,Rd
- Lb – theoretical length of the analyzed member
- E – Young's modulus of elasticity
- Ib – moment of inertia of the analyzed member
- Mj,Rd – joint design moment resistance
Capacity design (AISC)
Capacity design is a part of the seismic check and ensures that the joint has sufficient deformation capacity.
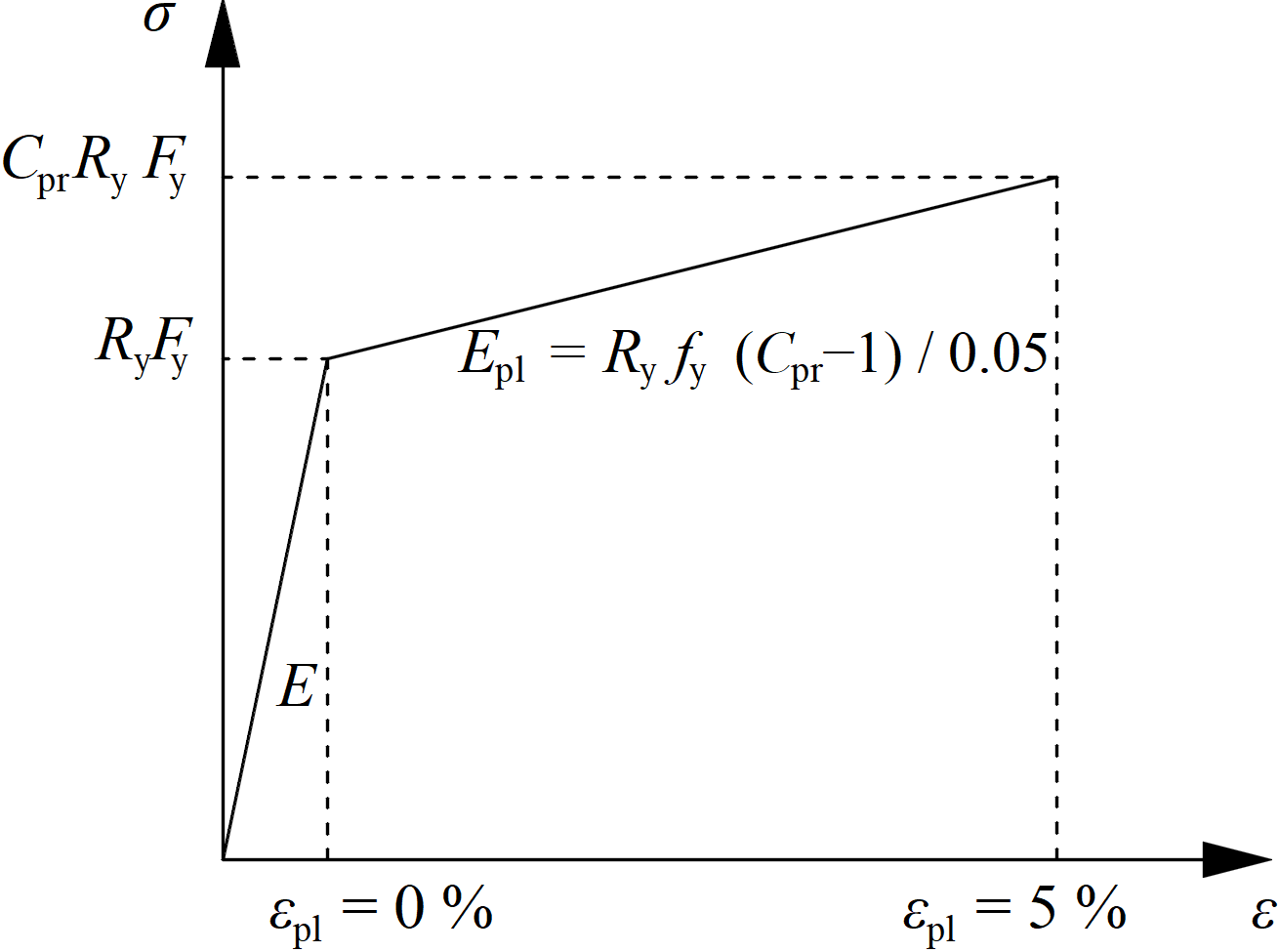
The objective of capacity design is to confirm a building undergoes controlled ductile behavior in order to avoid collapse in a design-level earthquake. Plastic hinge is expected to appear in dissipative item and all non-dissipative items of the joint must be able to safely transfer forces due to the yielding in the dissipative item. The dissipative item is usually a beam in moment resisting frame but it may also be e.g. an end plate. The safety factor is not used for dissipative items. Two factors are assigned to the yield strength of the dissipative item:
- Ry – ratio of probable to minimal yield strength – AISC 341-16 – Table A3.1; editable in materials
- \( C_{pr}=\frac{F_y+F_u}{2\bullet F_y} \le 1.2 \) – strain-hardening factor
The ultimate strength of the dissipative item is increased by factor Rt – ratio of probable to minimal tensile strength – AISC 341-16 – Table A3.1; editable in materials
The material diagram is modified according to the following figure:
The increased strength of the dissipative item allows for the input of loads that cause the plastic hinge to appear in the dissipative item. In the case of moment resisting frame and beam as the dissipative item, the beam should be loaded by My = CprRyFyZpl,y and corresponding shear forceVz = –2 My / Lh, where:
- Fy – characteristic yield strength
- Zpl,y – plastic section modulus
- Lh – distance between plastic hinges on the beam
In case of asymmetric joint, the beam should be loaded by both sagging and hogging bending moments and their corresponding shear forces.
The plates of dissipative items are excluded from check.