Steel connection material model
The most common material diagrams which are used in finite element modeling of structural steel are the ideal plastic or elastic model with strain hardening and the true stress-strain diagram. The true stress-strain diagram is calculated from the material properties of mild steels at an ambient temperature obtained in tensile tests. The true stress and strain may be obtained as follows:
\[ \sigma_{true}=\sigma (1 + \varepsilon) \]
\[ \varepsilon_{true}=\ln (1 + \varepsilon) \]
where σtrue is true stress, εtrue true strain, σ engineering stress, and ε engineering strain.
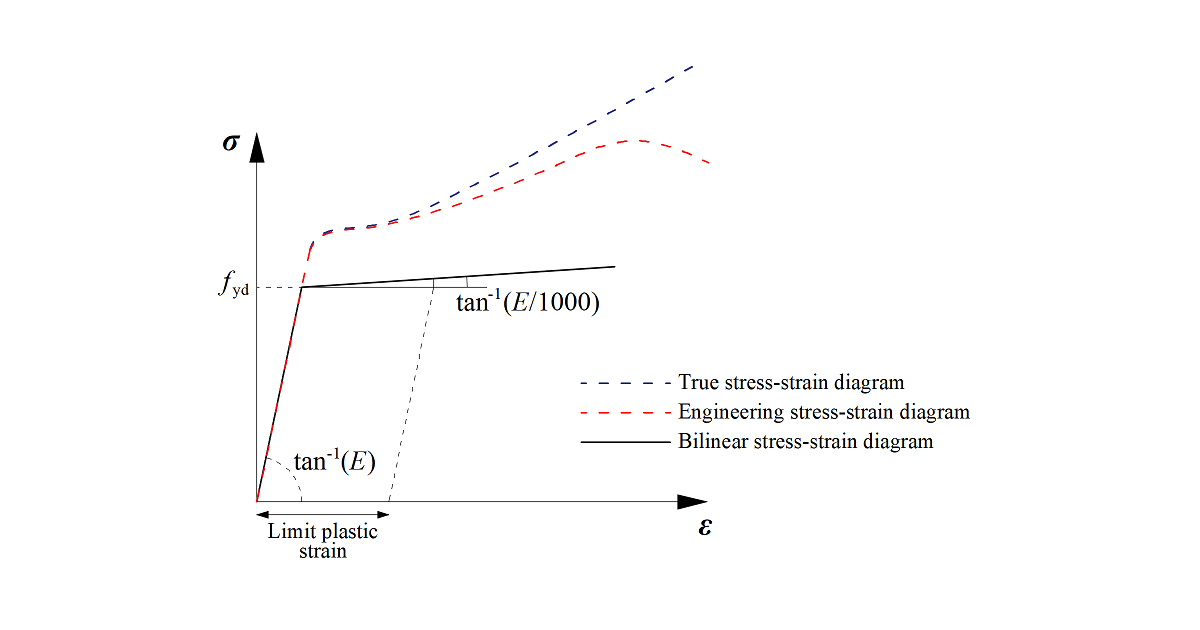
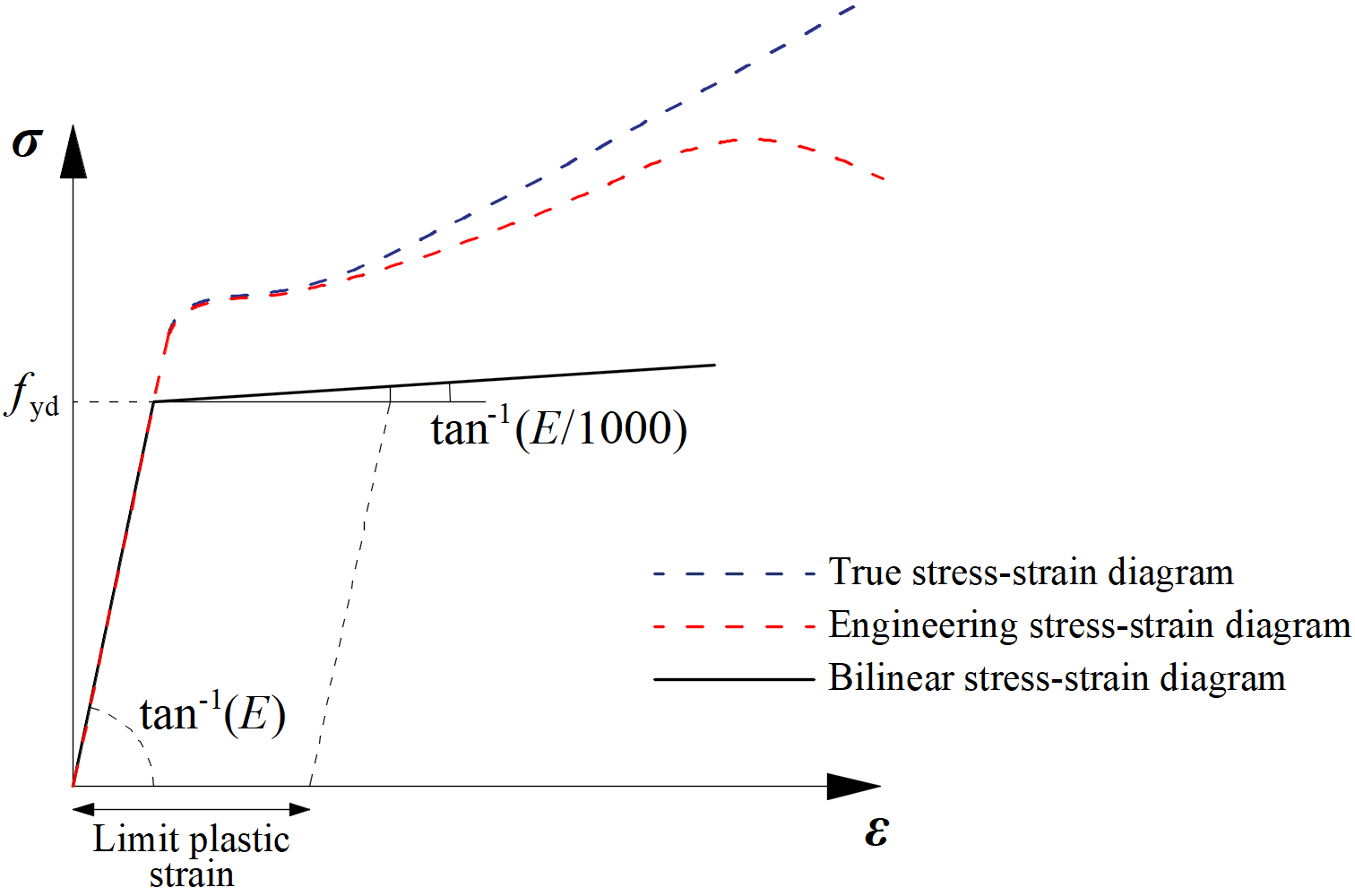
The plates in IDEA StatiCa Connection are modeled with elastic-plastic material with a nominal yielding plateau slope according to EN1993-1-5, Par. C.6, (2), tan-1 (E/1000). The material behavior is based on the von Mises yield criterion. It is assumed to be elastic before reaching the design yield strength, fyd.
The ultimate limit state criterion for regions not susceptible to buckling is reaching the limiting value of the principal membrane strain. The value of 5 % is recommended (e.g. EN1993-1-5, App. C, Par. C.8, Note 1).
Material diagrams of steel in numerical models
The limit value of plastic strain is often discussed. In fact, the ultimate load has low sensitivity to the limit value of plastic strain when the ideal plastic model is used. It is demonstrated in the following example of a beam to a column joint. An open section beam IPE 180 is connected to an open section column HEB 300 and loaded by bending moment. The influence of the limit value of plastic strain on the resistance of the beam is shown in the following figure. The limit plastic strain changes from 2 % to 8 %, but the change in moment resistance is less than 4 %.
An example of prediction of ultimate limit state of a beam to column joint
The influence of the limit value of plastic strain on the moment resistance