Fillet weld in lap joint

Description

The objective of this chapter is the verification of the component-based finite element method (CBFEM) of a fillet weld in a lap joint with the component method (CM). Two plates are connected in three configurations, namely with a transverse weld, with a longitudinal weld, and a combination of transverse and longitudinal welds. The length and throat thickness of the weld are the varying parameters in the study. The study also covers long welds whose resistance is reduced due to stress concentration. The joint is loaded by a normal force.

Analytical model

The fillet weld is the only component examined in the study. The welds are designed to be the weakest component in the joint. The weld is designed according to EN 1993-1-8:2005. The design resistance of the fillet weld is determined using the Directional method given in Cl. 4.5.3.2 in EN 1993-1-8:2005. The available calculation methods for checking the strength of fillet welds are based upon the simplifying assumption that stresses are uniformly distributed within a throat section of a fillet weld, leading to the normal stresses and shear stresses shown in Fig. 4.1.1, as follows:

• σ_⊥ is the normal stress perpendicular to the throat section;
• σ_∥ is the normal stress parallel to the axis of the weld in its cross-section;
• τ_⊥ is the shear stress (in the plane of the throat section) perpendicular to the axis of the weld;
• τ_∥ is the shear stress (in the plane of the throat section) parallel to the axis of the weld.

The normal stress σ_∥ parallel to the axis is not considered when verifying the design resistance of a weld.

$$\textsf{\textit{\footnotesize{Fig. 4.1.1 Stresses in a throat section of a fillet weld}}}$$

The design resistance of the fillet weld will be sufficient if the following are both satisfied:

$$\sqrt{\sigma_{\perp}^2 + 3 \cdot ( \tau_{\perp}^2 + \tau_{\perp}^2 )} \le \frac{f_\textrm{u}}{\beta_\textrm{w} \gamma_\textrm{M2}}$$

$$\sigma_{\perp} \le \frac{0.9 f_\textrm{u}}{\gamma_\textrm{M2}}$$

In lap joints longer than $150 \cdot a$, the reduction factor $\beta_{\mathrm{Lw,1}}$ is given by:

$\beta_{\mathrm{Lw,1}} = 1.2 - \frac{0.2 L_\textrm{j}}{150 a}$  but   $\beta_{\mathrm{Lw,1}} \le 1.0$

Numerical model

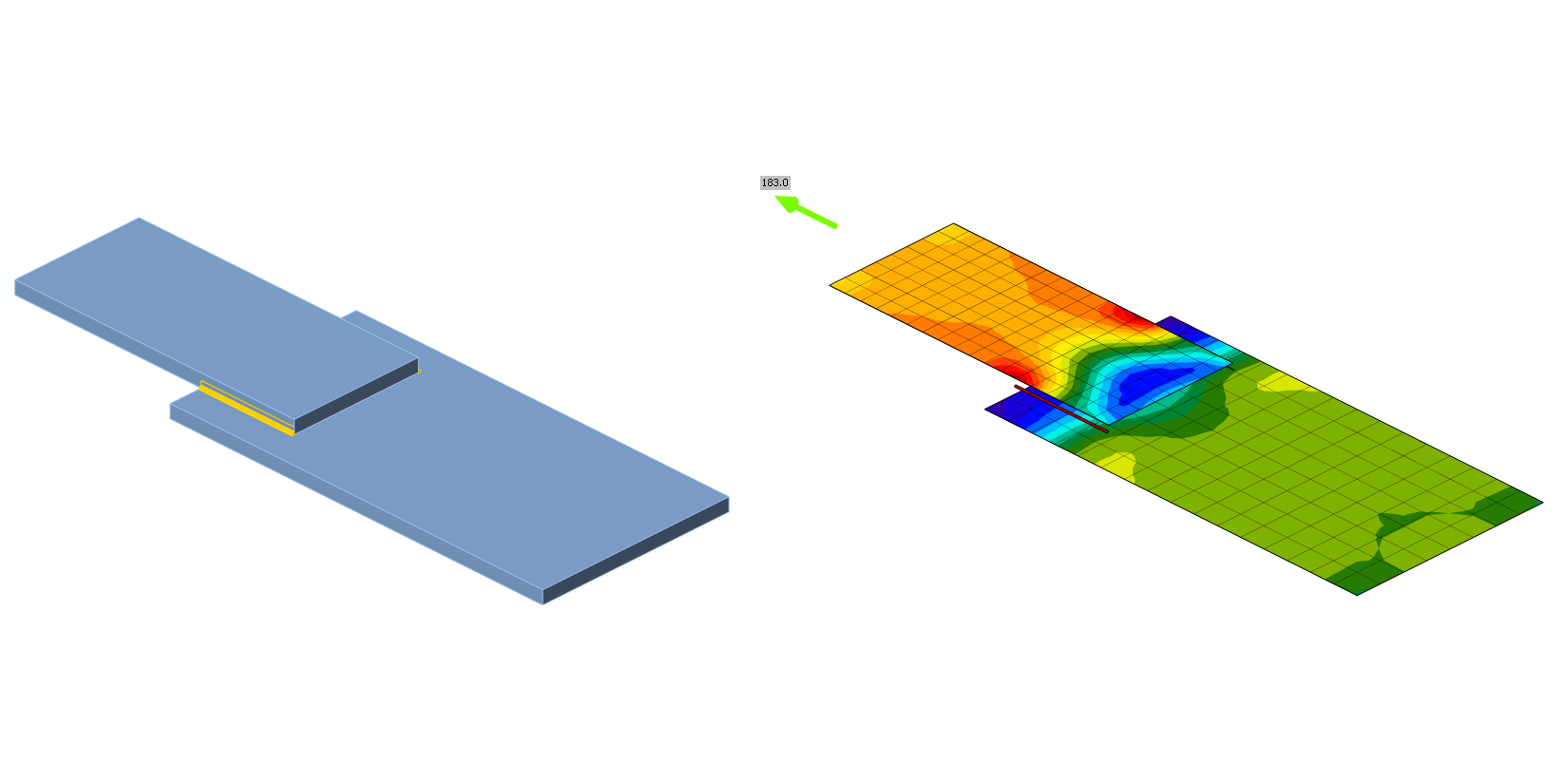
The weld component in CBFEM is described in General theoretical background and EN theoretical background. Nonlinear elastic-plastic material is used for welds in this study. The limiting plastic strain is reached in the longer part of the weld, and stress peaks are redistributed.

Verification of resistance

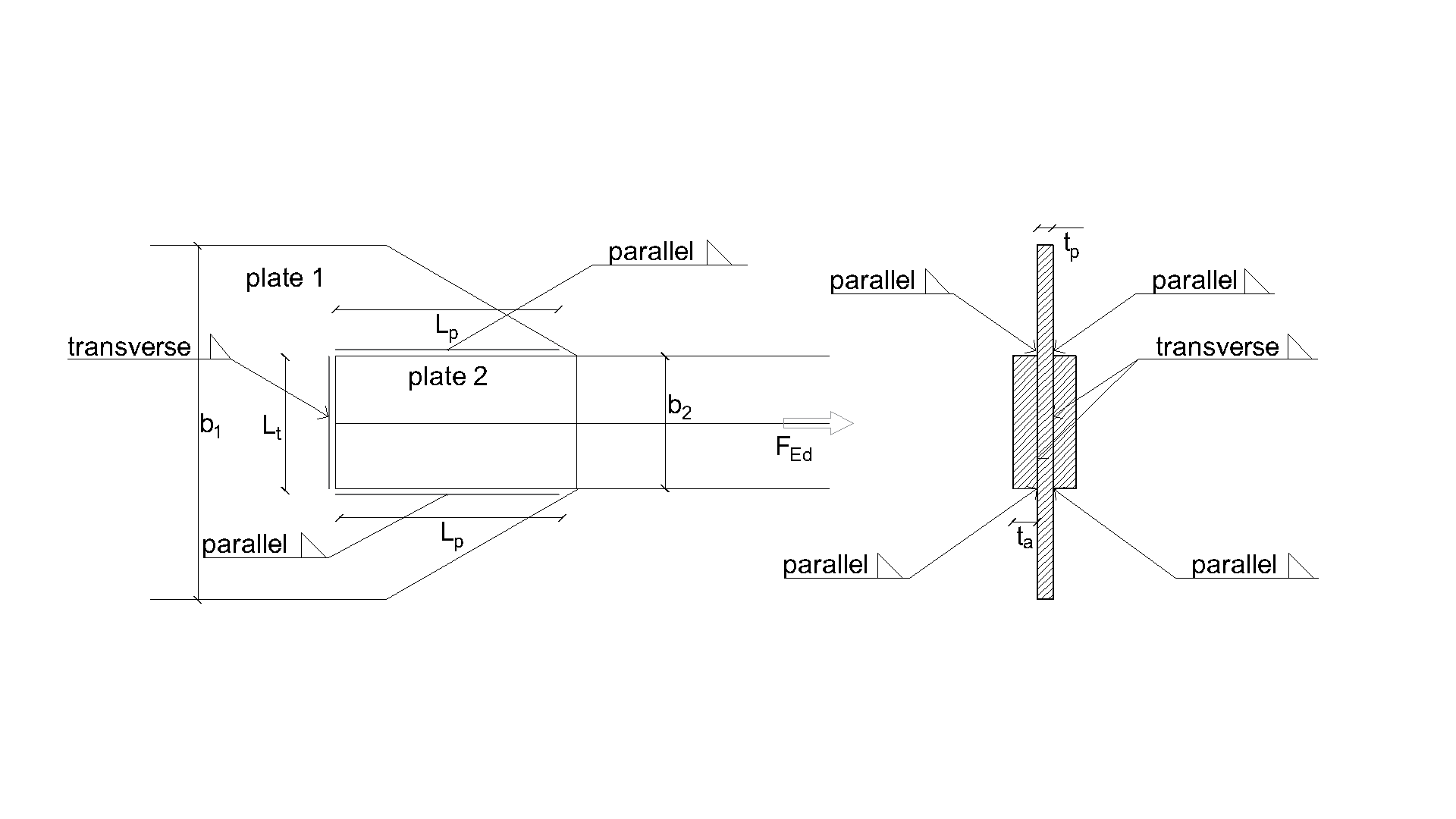
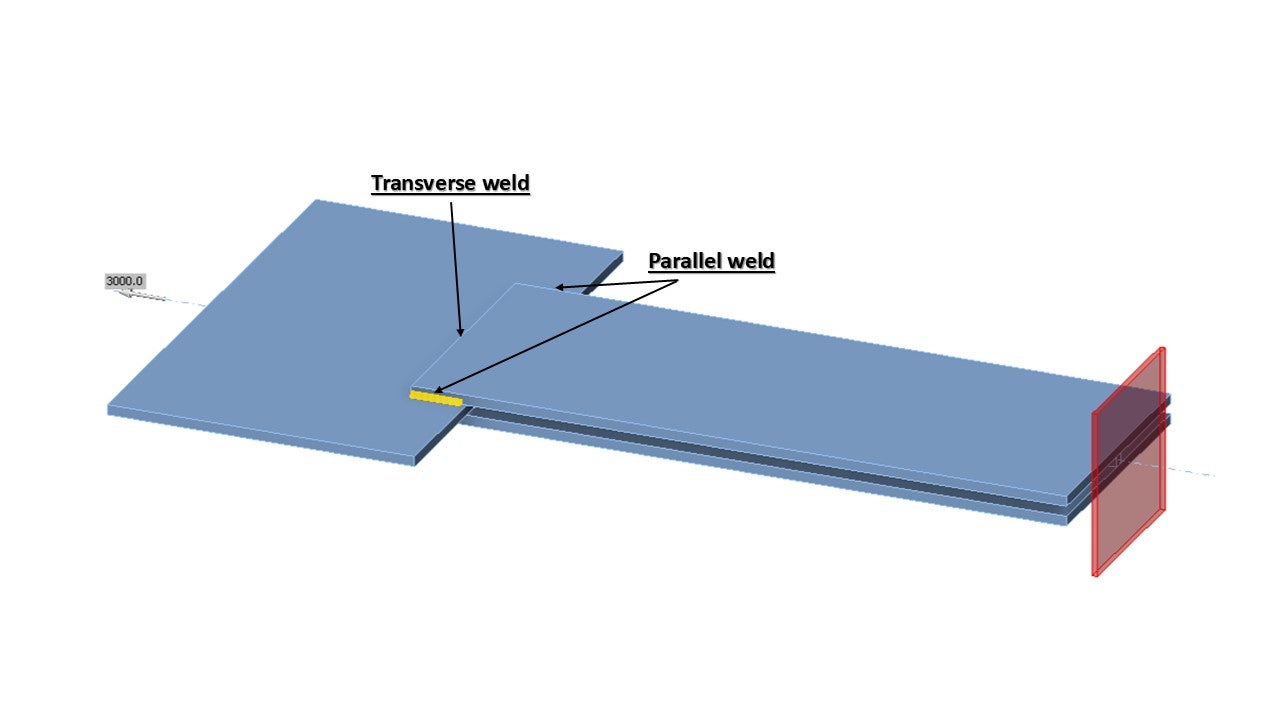
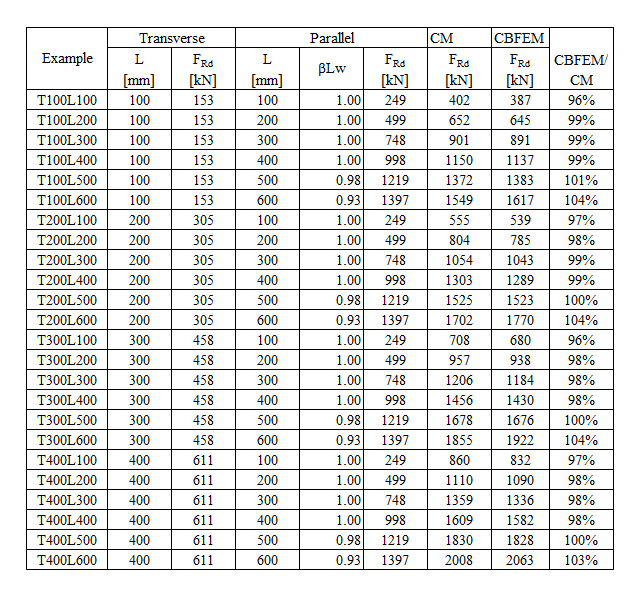
An overview of the considered examples and the material properties is provided in Tab. 4.1.1. The weld configurations are T for transverse, P for parallel weld, and TP for a combination of both; see the geometry in Fig. 4.1.2. The steel grade was S235 (f_y = 235 MPa, f_u = 360 MPa, E = 210 GPa, β_w = 0,8). Partial safety factors were γ_M0 = 1.0, γ_M2 = 1.25. The geometry of the model is shown in Fig. 4.1.2. The plates have a thickness of 20 mm. The connection is symmetrical, and the plate is pulled out of the welded splice connection. The length and width of the plates are adjusted according to the length of the parallel and transverse weld. The weld resistance is always the governing failure mode. The weld throat thickness is 3 mm. The lengths of the transverse and parallel welds vary in this parametric study.

$$\textsf{\textit{\footnotesize{Drawing 4.1 Joint geometry with dimensions}}}$$

Design weld resistance calculated by CBFEM is compared with the results of CM. The results are presented in Tab. 4.1.1 – 4.1.3 and Fig. 4.1.3 – 4.1.5.

$$\textsf{\textit{\footnotesize{Fig. 4.1.2 Specimen geometry}}}$$

Transverse welds resistance calculation 

$$\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}$$

$$\sigma_{\perp} = \tau_{\perp} = \frac{\sigma_\textrm{N}}{\sqrt{2}} = \frac{N}{L_{\textrm{t}} \cdot a}\cdot \frac{1}{\sqrt{2}}$$

$$\tau_{\parallel} = 0$$

$$\sqrt{ \left( \frac{\sigma_\textrm{N}}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{\sigma_\textrm{N}}{\sqrt{2}} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}$$

$$\sqrt{ \left( \frac{N}{L_{\textrm{t}}\cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{N}{L_{\textrm{t}}\cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}$$

$$N \leq \frac{f_\textrm{u} \cdot L_{\textrm{t}}\cdot a }{\beta_{\textrm{w}}  \cdot  \gamma_{\textrm{M2}}  \cdot  \sqrt{2}}$$

$$\sigma_{\perp}= \frac{N}{L_{\textrm{t}} \cdot a}\cdot \frac{1}{\sqrt{2}} \leq \frac{f_\textrm{u}  \cdot  0.9}{ \gamma_{\textrm{M2}}}$$

$$N \leq \frac{f_{u}  \cdot L_{\textrm{t}}\cdot  a  \cdot  0.9  \cdot  \sqrt{2}}{ \gamma_{\textrm{M2}} }$$

Where:

$a$ - weld throat thickness

$N$ - the normal force acting on the beam

$L_{\textrm{t}}$ - total transverse weld length 

$\beta_{\mathrm{w}}$ - correlation factor taken from EN 1993-1-8 Table 4.1

$f_\textrm{u}$ - nominal ultimate tensile strength of the weaker part joined

$\gamma_{\mathrm{M2}}$ - partial safety factor for welds

Parallel weld resistance calculation

$$\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}$$

$$\sigma_{\perp} = \tau_{\perp} = 0$$

$$\tau_{\parallel} = \frac{V}{L_{\textrm{p}}  \cdot  a}$$

$$\sqrt{  3 \cdot \left( \tau_{\parallel} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}$$

$$\sqrt{  3 \cdot \left(  \frac{V}{L_{\textrm{p}} \cdot a}\right)^2} \leq \frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}$$

$$V = \frac{f_\textrm{u}  \cdot  L_{\textrm{p}} \cdot  a  \cdot  \beta_{\mathrm{Lw1}}}{\beta_{\mathrm{w}}  \cdot  \gamma_{\mathrm{M2}}  \cdot  \sqrt{3}}$$

Where:

$a$ - weld throat thickness

$V$ - shear force acting on beam

$L_{\textrm{t}}$ - total parallel welds length

$\beta_{\mathrm{w}}$ - correlation factor taken from EN 1993-1-8 Table 4.1

$\beta_{\mathrm{Lw1}}$ - long weld reduction factor, EN 1993-1-8 Equation 4.9

$f_\textrm{u}$ - nominal ultimate tensile strength of the weaker part joined

$\gamma_{\mathrm{M2}}$ - partial safety factor for welds

Transverse and parallel calculation 

The resistance calculated by hand for a transverse and parallel weld combination is simply the sum of the transverse and parallel resistances derived from the equations above. 

Results Presentation

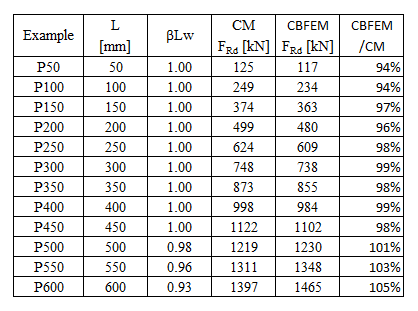
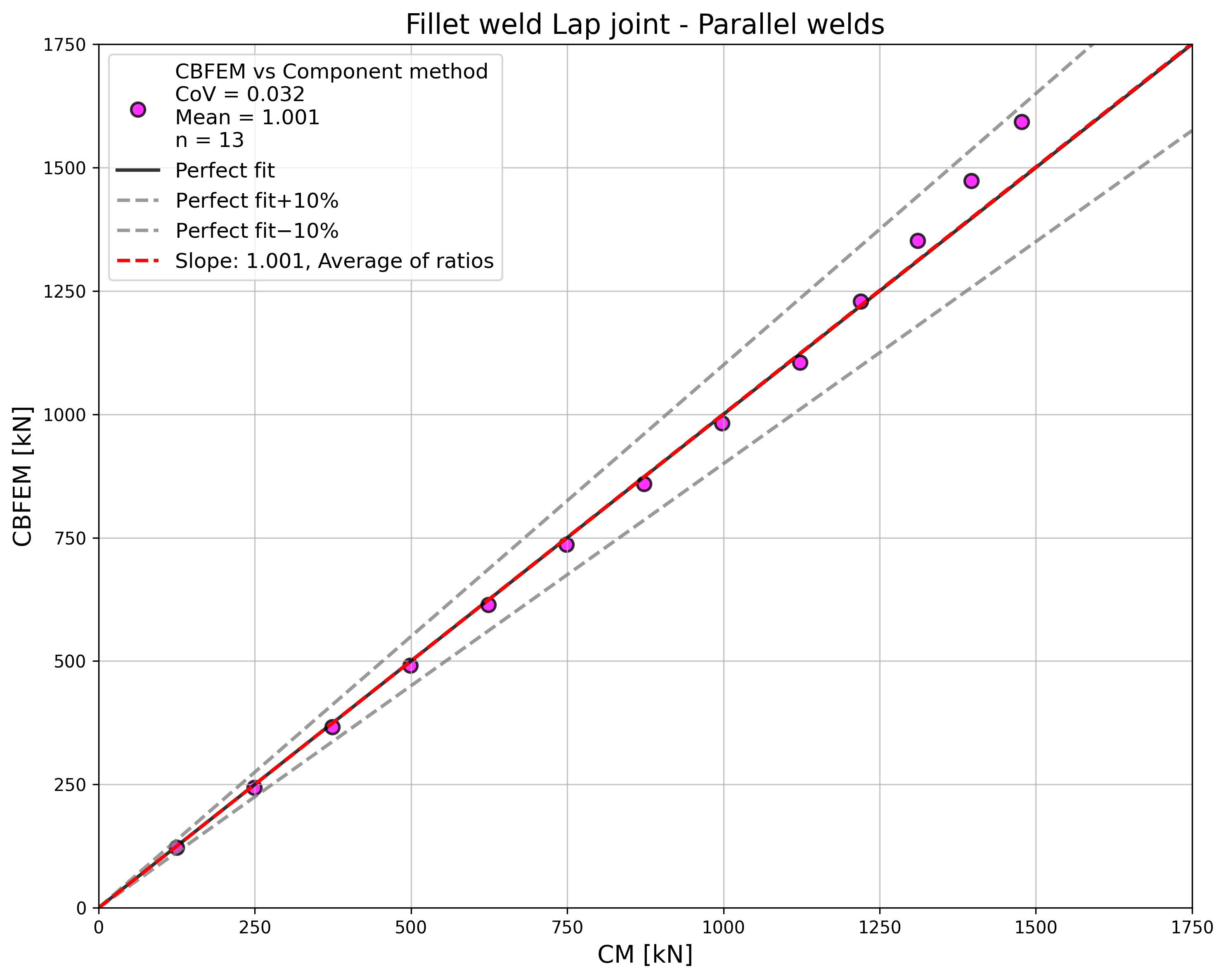
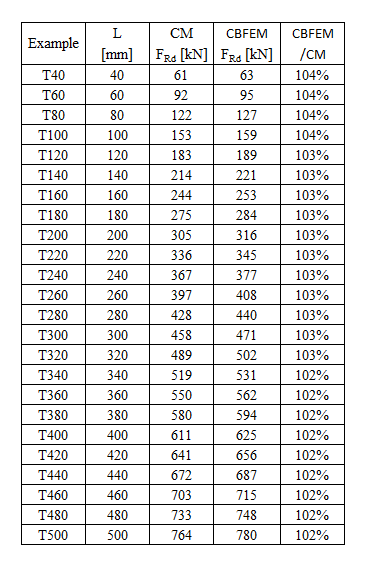
$$\textsf{\textit{\footnotesize{Tab. 4.1.1 Parallel welds results}}}$$

$$\textsf{\textit{\footnotesize{Fig. 4.1.3 Comparison of load resistances of parallel welds}}}$$

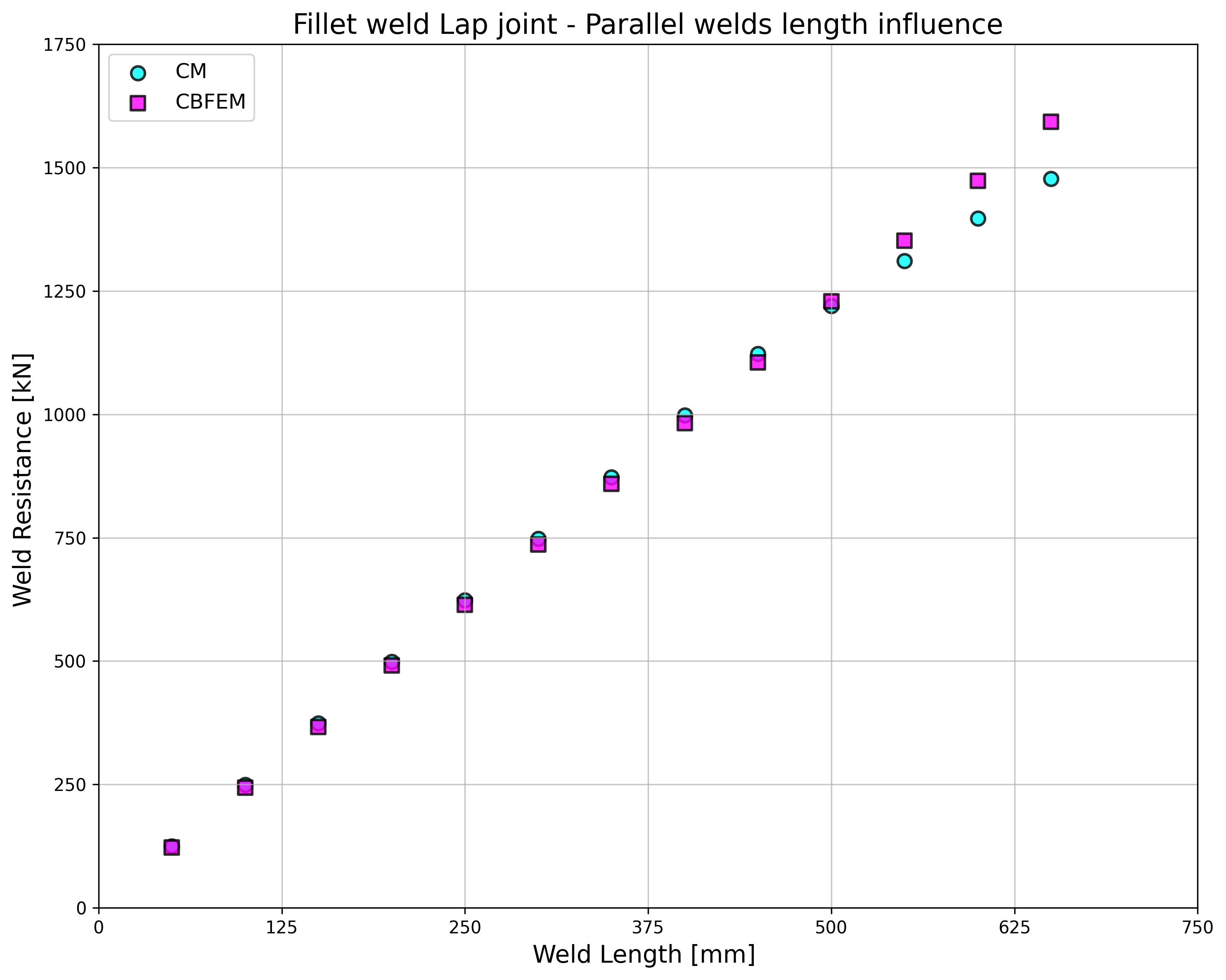
$$\textsf{\textit{\footnotesize{Fig. 4.1.3.a Influence of weld length on resistance}}}$$

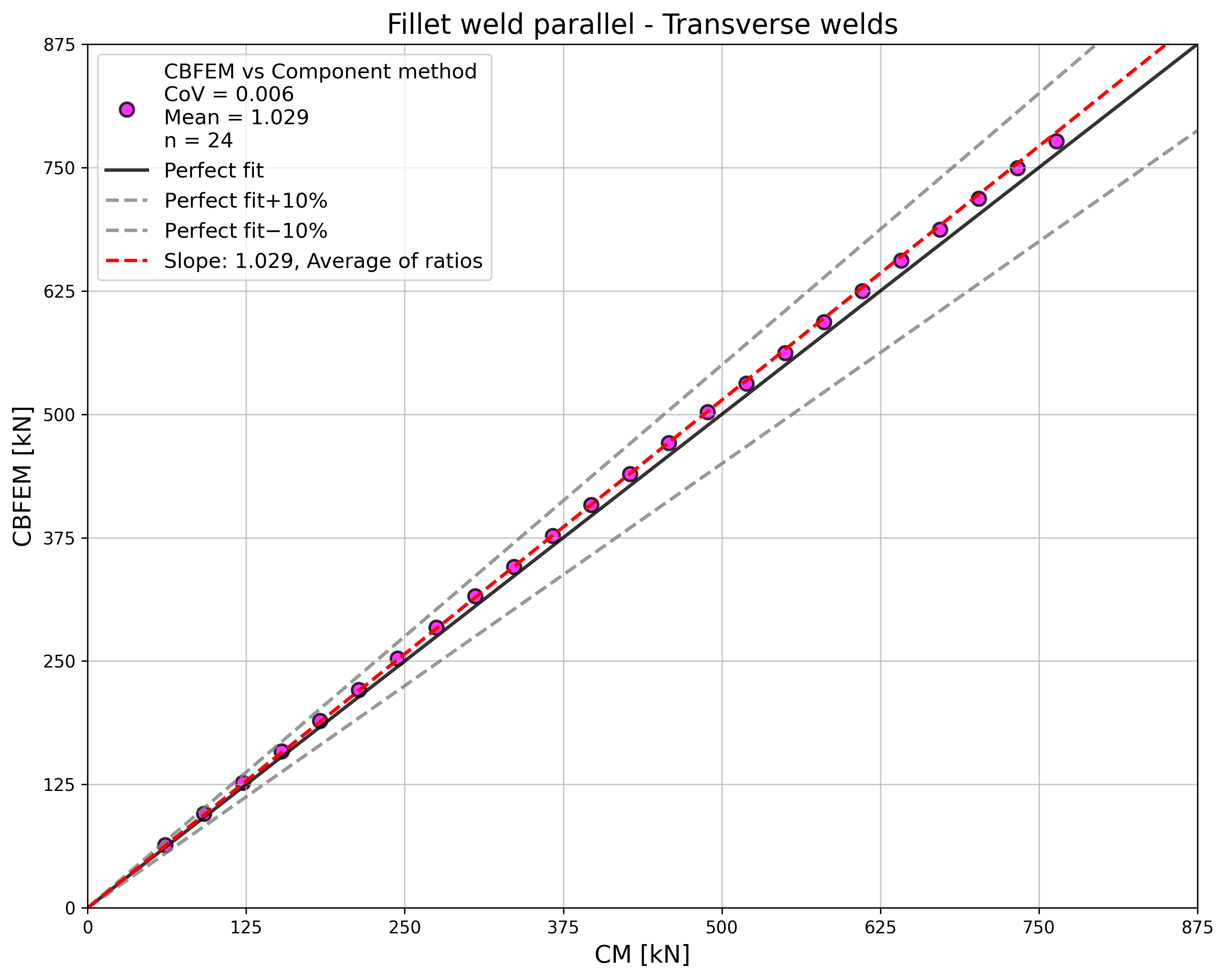
$$\textsf{\textit{\footnotesize{Tab. 4.1.2 Transverse welds}}}$$

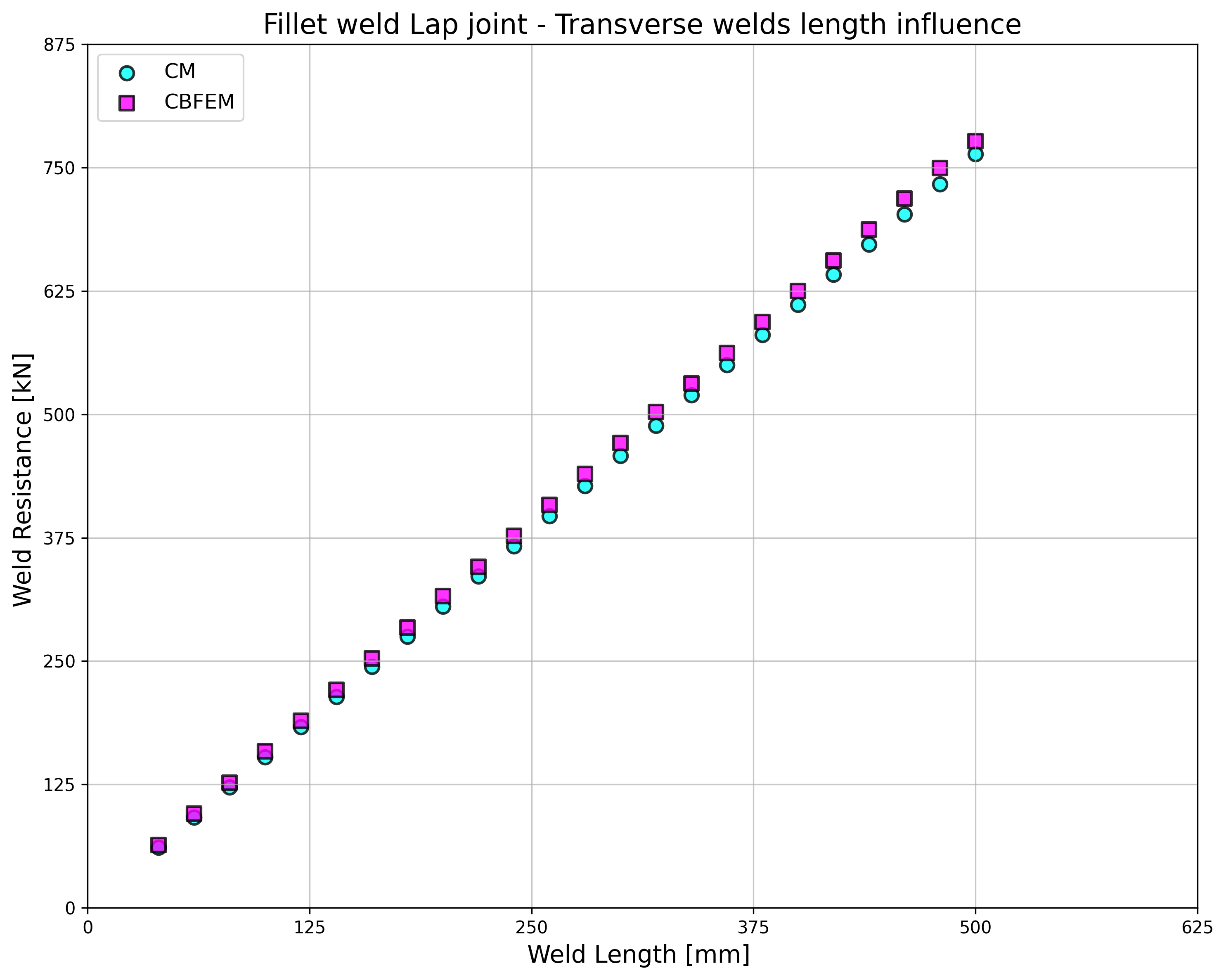
$$\textsf{\textit{\footnotesize{Fig. 4.1.4 Comparison of load resistances of transverse welds}}}$$

$$\textsf{\textit{\footnotesize{Fig. 4.1.4.a Influence of weld length on resistance}}}$$

$$\textsf{\textit{\footnotesize{Tab. 4.1.3 Grouped welds}}}$$

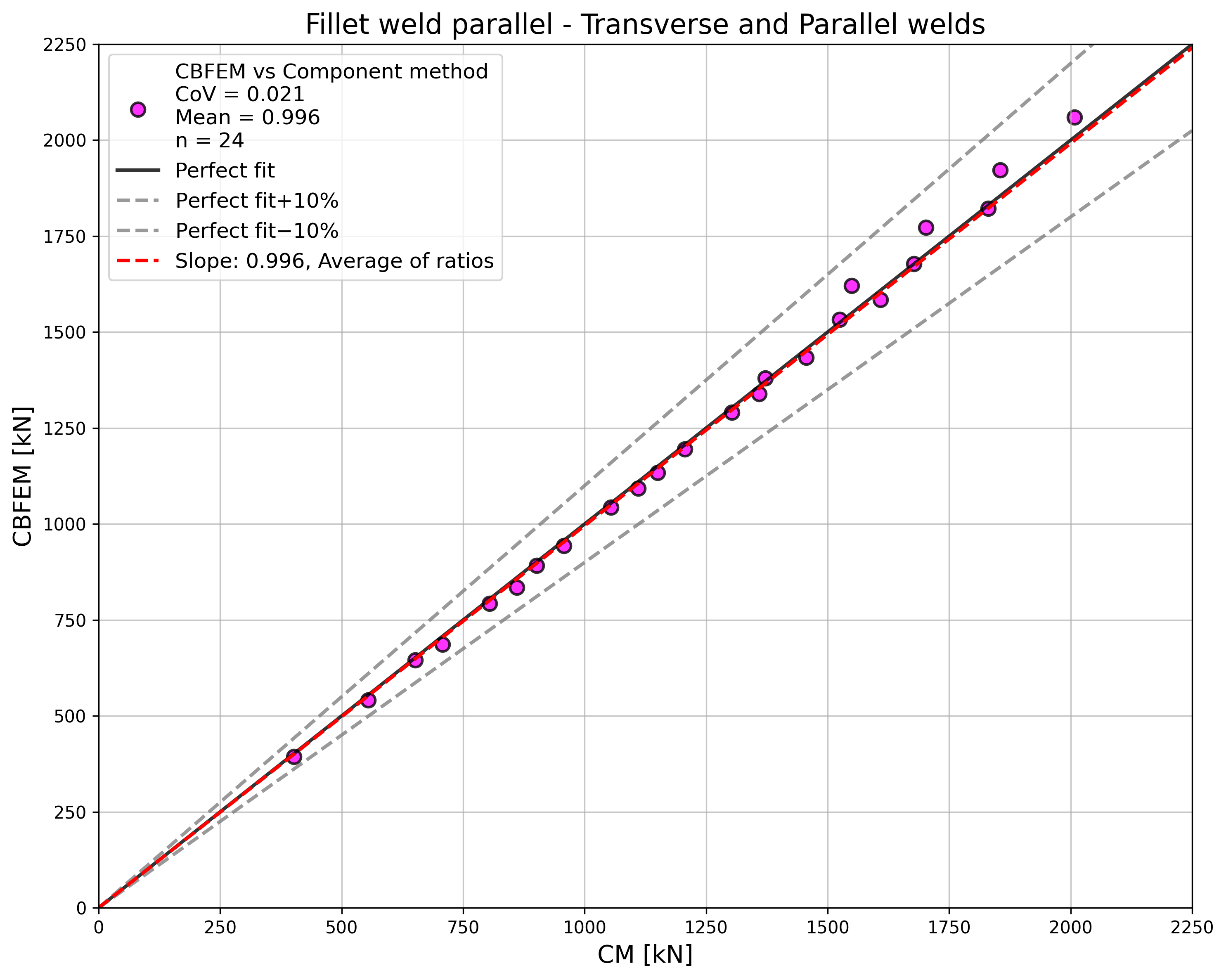
$$\textsf{\textit{\footnotesize{Fig. 4.1.5 Comparison of load resistances of group}}}$$

The resistance of parallel welds, transverse welds, and multi-oriented weld groups is nearly identical according to CM and CBFEM. The biggest difference in this study is 6% in load resistance.

The CBFEM results of parallel welds are slightly conservative but start to diverge for long welds. The reduction of resistance due to long welds is not captured by CBFEM, but it is not expected that welds longer than 200×throat thickness could appear in any connection, and up to this length, the results are still very close.

For transverse welds, CBFEM provides very consistent results with 2–4% higher resistance.

Benchmark example

Inputs

Member 1 – Iw60x500

• Welded from plates with thickness t = 20 mm

• Width b = 500 mm

• Web is removed by Opening manufacturing operation

• Steel S235

Member 2 – Plate 20x1000

• Thickness t = 20 mm

• Width b = 1000 mm

• Steel S235

• Offset e_x = –90 mm

Transverse fillet weld at both sides of Member 2

• Throat thickness a = 3 mm

• Weld length L_t = 100 mm

Parallel fillet weld at both sides of Member 2

• Throat thickness a = 3 mm

• Weld length L_p = 100 mm

Output

• Design resistance in tension F_Rd = 387 kN (It should be noted that the resistance was calculated using the "Stop at limit strain" function. Consequently, the actual CBFEM resistance may be marginally higher.)