Extended End-Plate Moment Connections (AISC)
This verification example was prepared by Mark D. Denavit and Kayla Truman-Jarrell in a joint project of The University of Tennessee and IDEA StatiCa.
1 Description
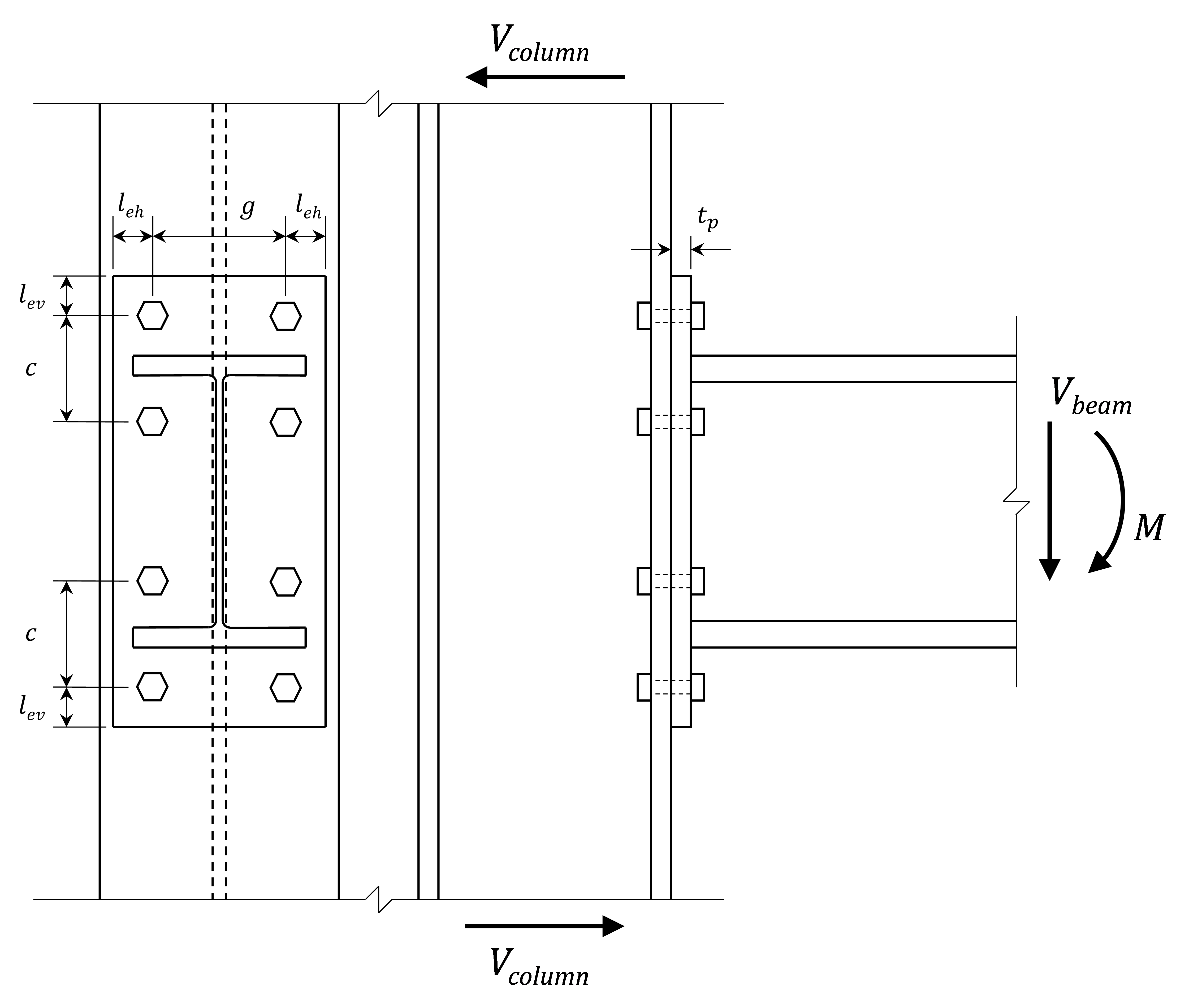
A comparison between results from the component-based finite element method (CBFEM) and traditional calculation methods used in US practice for extended end-plate moment connections (Fig. 1) is presented in this study.
Fig. 1 Schematic of the extended end-plate moment connection investigated in this study
The traditional calculation methods used in this work for non-seismic connections are based upon the recommendations presented in AISC Design Guide 4 (Murray and Sumner 2003) in addition to the requirements for load and resistance factor design (LRFD) in the AISC Specification (2016a). The traditional calculation methods used in this work for seismic (i.e., capacity designed) connections are based upon AISC Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications (2016b), hereafter referred to as AISC 358. For both seismic and non-seismic connections, these references include minimum end-plate thickness and column flange thickness limitations that are not directly based on the applied loads. These limits are intended to avoid prying action and ensure that the connection is fully restrained. For non-seismic connections, it is permitted to use thinner plates and column flanges if prying action is considered, for example using the recommendations from Dowswell (2011). However, the minimum thickness limits were enforced for all traditional calculations in this study.
The limit states evaluated in the traditional calculations include tensile rupture of the bolts, flexural yielding of the end plate and column flange (via thickness limitations), shear yielding and rupture of the end plate, local column limit states (i.e., web local yielding, web local crippling, and web compression buckling), column web panel-zone yielding, bolt shear limit states (i.e., bolt shear rupture, bearing, tearout – note only the shear strength of the compression bolts was considered). For simplicity, all welds were modeled as butt welds and their strength was not evaluated in the traditional calculations.
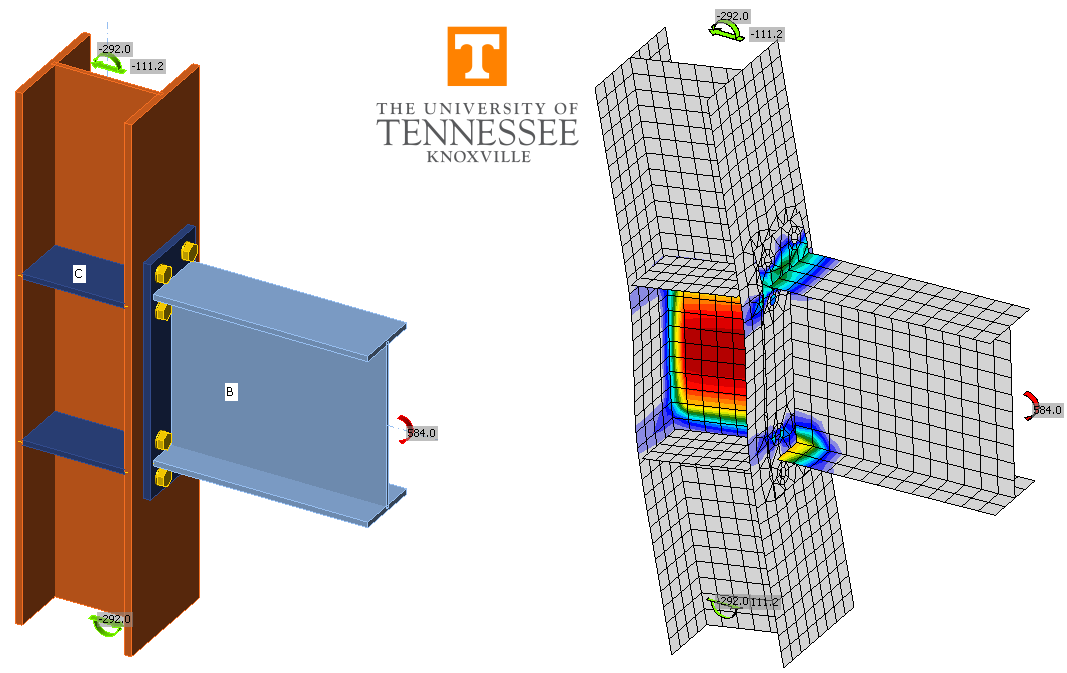
The CBFEM results were obtained from IDEA StatiCa Version 21.0. Example models are shown in Fig. 2. The maximum permitted loads were determined iteratively by adjusting the applied load input to a value that the program deems safe but if increased by a small amount (e.g., 1 kip-in.) the program would deem unsafe. In contrast to the traditional calculations, the influence of prying was evaluated in IDEA StatiCa and results shown include cases with prying action. The rigidity of the connection was evaluated using stiffness analyses (i.e., “ST” analysis type).
Fig. 2 Extended end-plate moment connections modeled in IDEA StatiCa.
2 End-Plate Thickness
First, the impact of end-plate thickness on the behavior and strength of the connection is investigated. For these comparisons, the beam is a W21×68, and the column is a W14×193. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The column was selected to be large (tf = 1.44 in.) and provided with 5/8 in. thick stiffeners (i.e., continuity plates) to ensure that the controlling limit state was not in the column. The end plate has a depth of 29 in., a width of 9.5 in., and thickness varies from 3/8 in. to 2.5 in. All plate material (i.e., end plate and stiffeners) conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi). The connection has four bolts near each beam flange (8 total bolts) and the end plate is not stiffened. This configuration is commonly referred to as a four-bolt unstiffened, 4E, configuration. The bolts are 1-1/8 in. diameter A325 with a horizontal gage of g = 5.5 in. and vertical spacing of c = 4.5 in. The vertical distance from the centerline of the bolts to the edge of the end plate is lev = 2 in.
In IDEA StatiCa, loads were applied using the “loads in equilibrium” option. The moments applied at the top and the bottom of the column were each equal to half the moment applied to the beam. A shear load of 25 kips was also applied to the column (Vcolumn = 25 kips, Fig. 1). For simplicity, no shear was applied to the beam (Vbeam = 0 kips, Fig. 1).
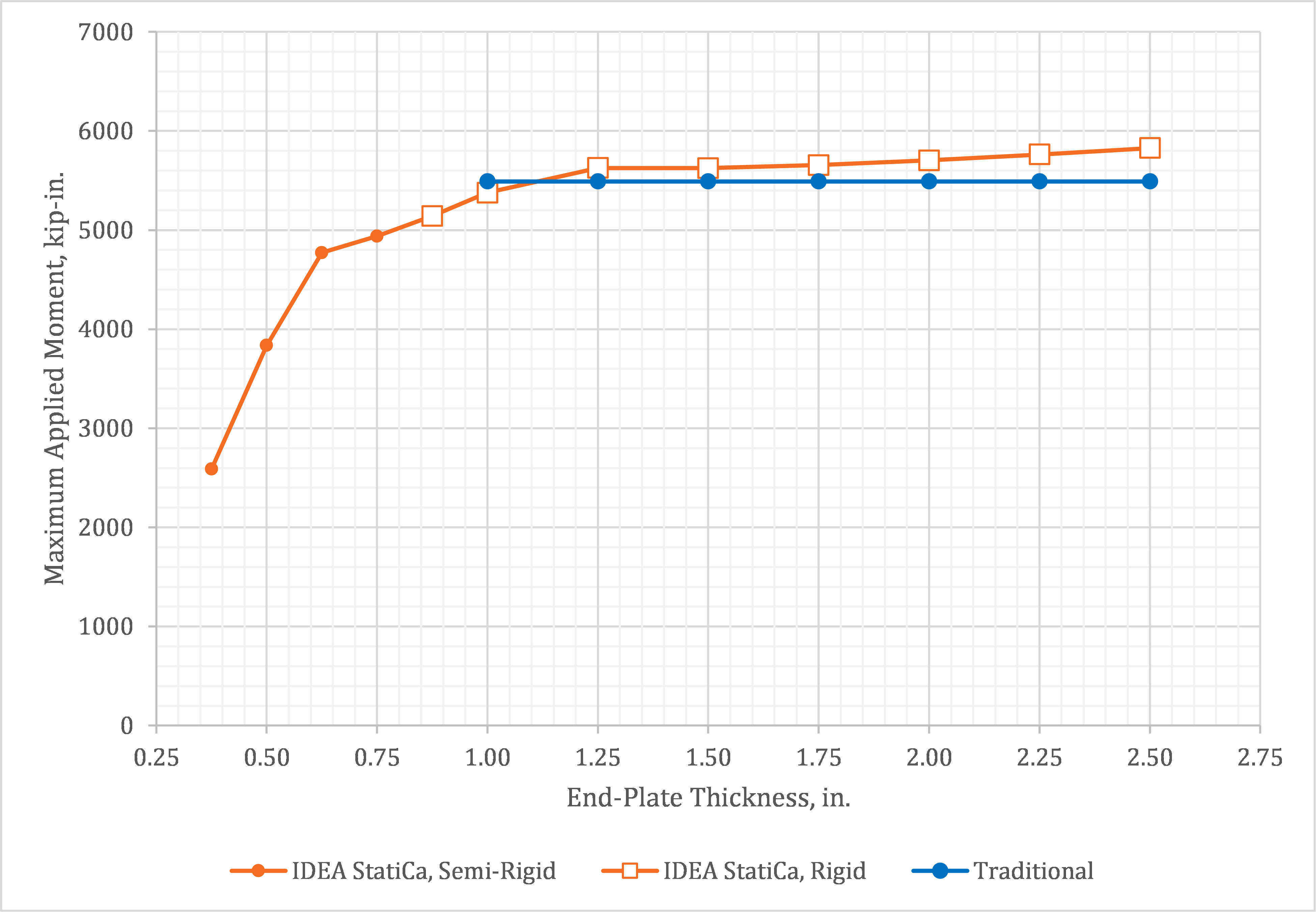
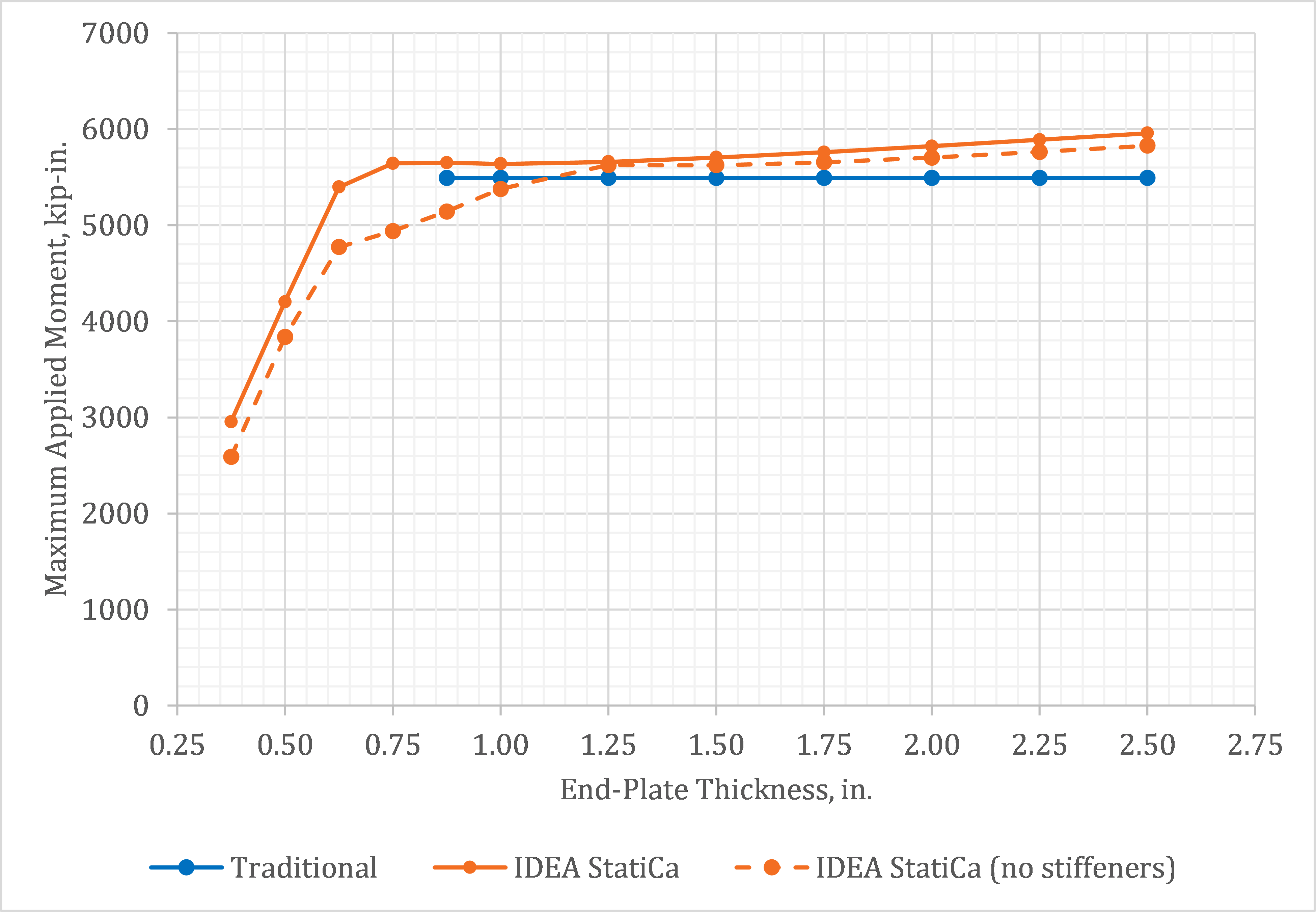
Variation of the maximum applied moment with end-plate thickness is presented in Fig. 3. The controlling limit state for each thickness is presented in Table 1. Results are not shown for the traditional calculations for end-plate thicknesses less than 1 in. since thinner plates did not meet the minimum thickness requirements to avoid prying action. The controlling limit state from the traditional calculations for the connections that met the end-plate thickness requirement was tensile rupture of the bolts. As a result, the maximum applied moment does not vary with end-plate thickness.
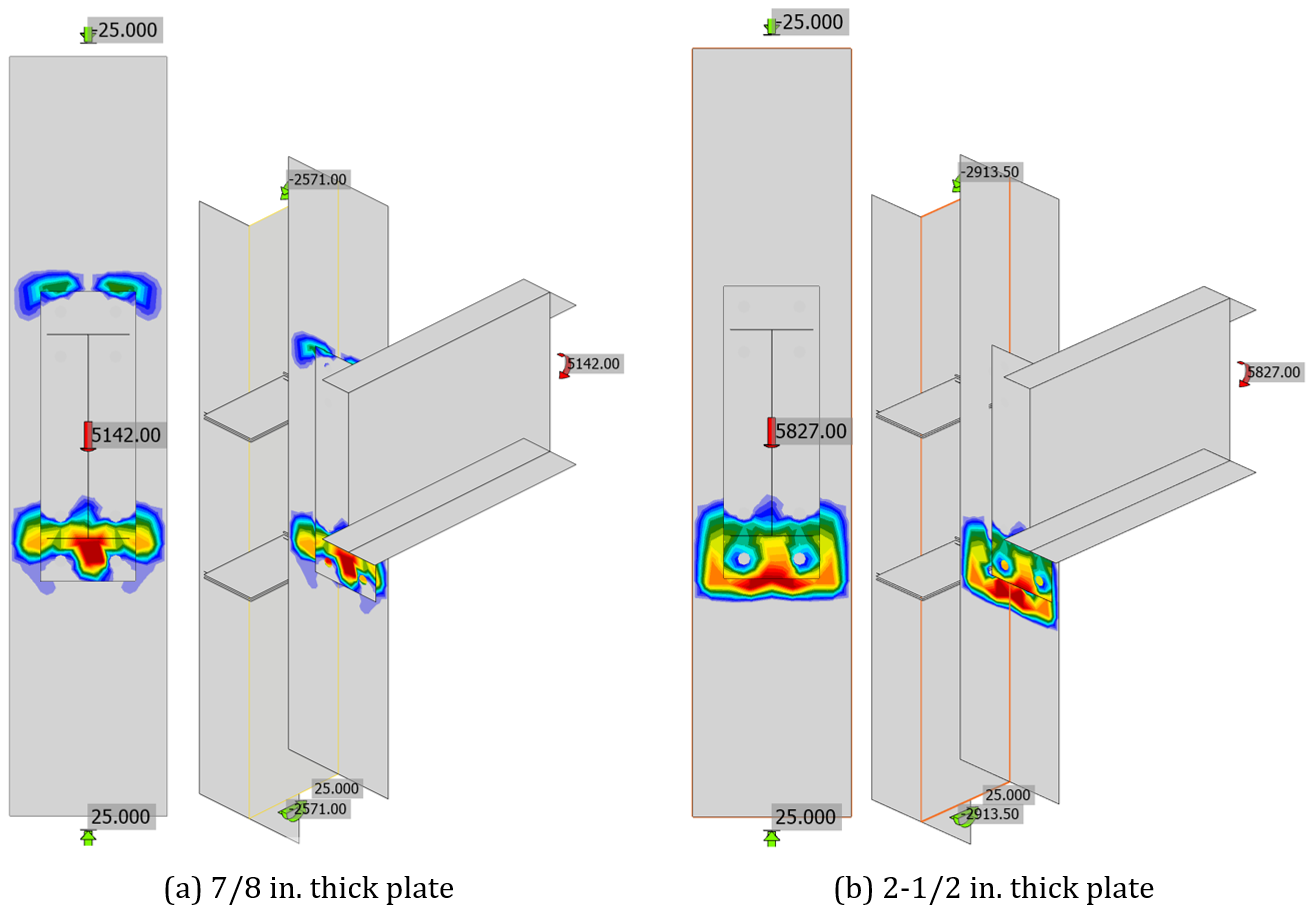
Variation of maximum applied moment with end-plate thickness is seen in the IDEA StatiCa results. For very thin plates (t ≤ 0.5 in.), plastic strain in the end plate controls the design. Otherwise, bolt tension controls the design. The maximum applied moment increases with increasing end-plate thickness over the entire range investigated. The increase in maximum applied moment is rapid for thin plates as increasing thickness directly increases the flexural yielding strength of the end plate. The increase in maximum applied moment is more gradual when bolt tension controls. For end-plate thicknesses 1.25 in. and greater, the maximum applied moment for IDEA StatiCa exceeds that from the traditional calculations. The reason for this is that the traditional calculations assume that the contact force at the interface between the column flange and the end plate is centered about the beam flange whereas IDEA StatiCa models the contact pressure explicitly. As the end-plate thickness increases, the portion of the end plate that extends past the beam flange is stiffer and more capable of resisting contact pressure, shifting the compressive force below the beam bottom flange (Fig. 4). Therefore, while the tensile capacity of the bolts is no different between IDEA StatiCa and the traditional calculations, the lever arm of the couple is greater for IDEA StatiCa resulting in greater moment capacity.
For each end-plate thickness, the presence of prying action and the rigidity of the connection were determined by IDEA StatiCa. A connection was assumed to have prying action if there was contact stress on the tension side of the connection. For example, as shown in Fig. 4 prying action was observed for the connection with a 7/8 in. thick plate, but not for the connection with the 2-1/2 in. thick plate. There was no prying action for end-plate thicknesses of 1 in. and greater. This agrees with the corresponding minimum thickness limitation of the traditional calculations. Connections with end-plate thicknesses of 7/8 in. and greater were determined to be fully restrained (i.e., rigid) by a stiffness analysis in IDEA StatiCa, indicating that the minimum thickness limitation of the traditional calculations also provides a good indirect check of the rigidity of the connection for this case.
Fig. 3 Maximum applied moment vs. end-plate thickness
Table 1. Controlling limit state for results presented in Fig. 3
| End-Plate Thickness, in. | IDEA StatiCa | Traditional |
| 0.375 | Plastic strain (end plate) | N/A |
| 0.500 | Plastic strain (end plate) | N/A |
| 0.625 | Bolt tension | N/A |
| 0.750 | Bolt tension | N/A |
| 0.875 | Bolt tension | N/A |
| 1.000 | Bolt tension | Bolt tension |
| 1.250 | Bolt tension | Bolt tension |
| 1.500 | Bolt tension | Bolt tension |
| 1.750 | Bolt tension | Bolt tension |
| 2.000 | Bolt tension | Bolt tension |
| 2.250 | Bolt tension | Bolt tension |
| 2.500 | Bolt tension | Bolt tension |
Fig. 4 Contact stress for results presented in Fig. 3
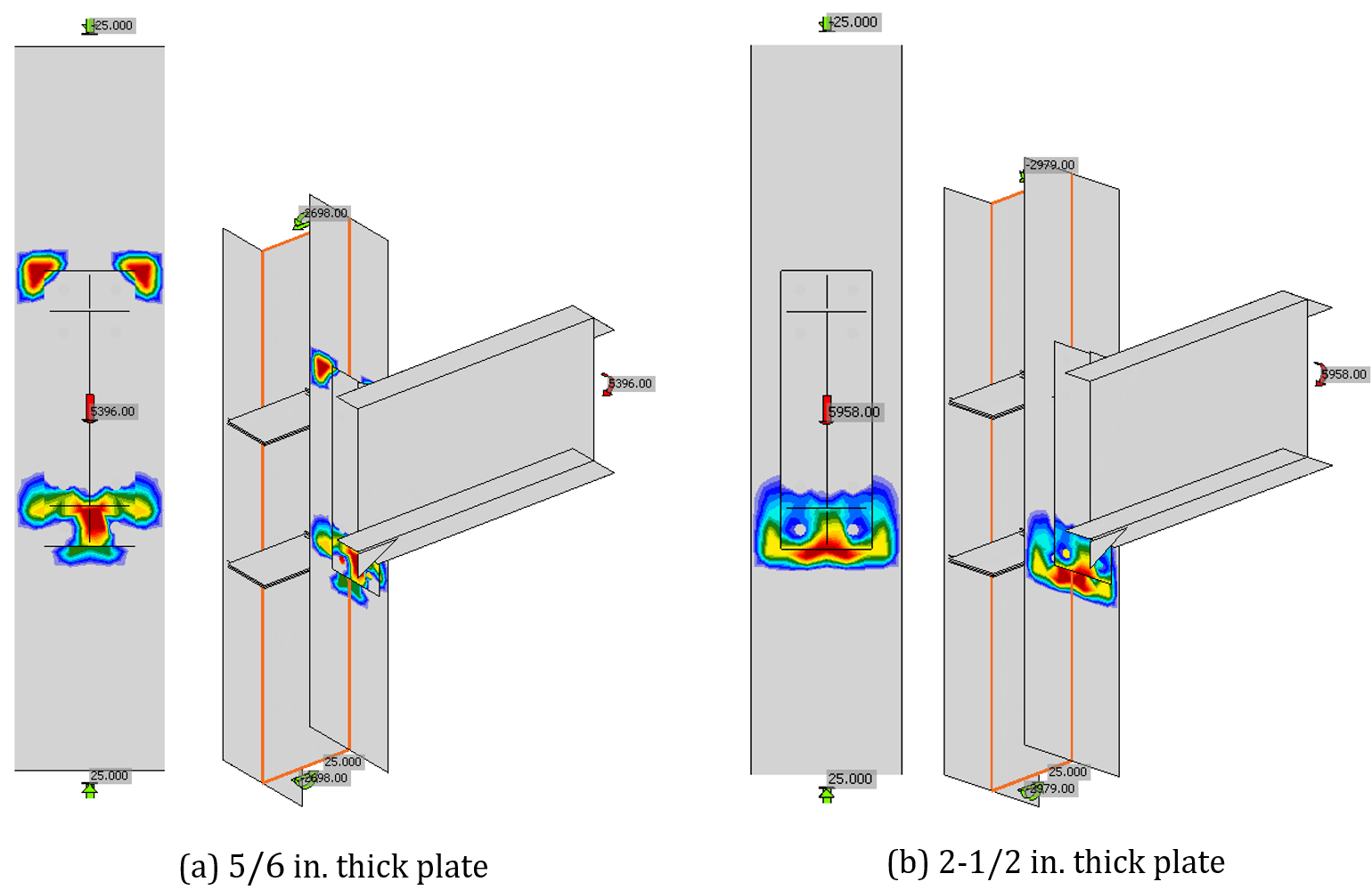
Fig. 5 Contact stress for results presented in Fig. 6(with end plate stiffener)
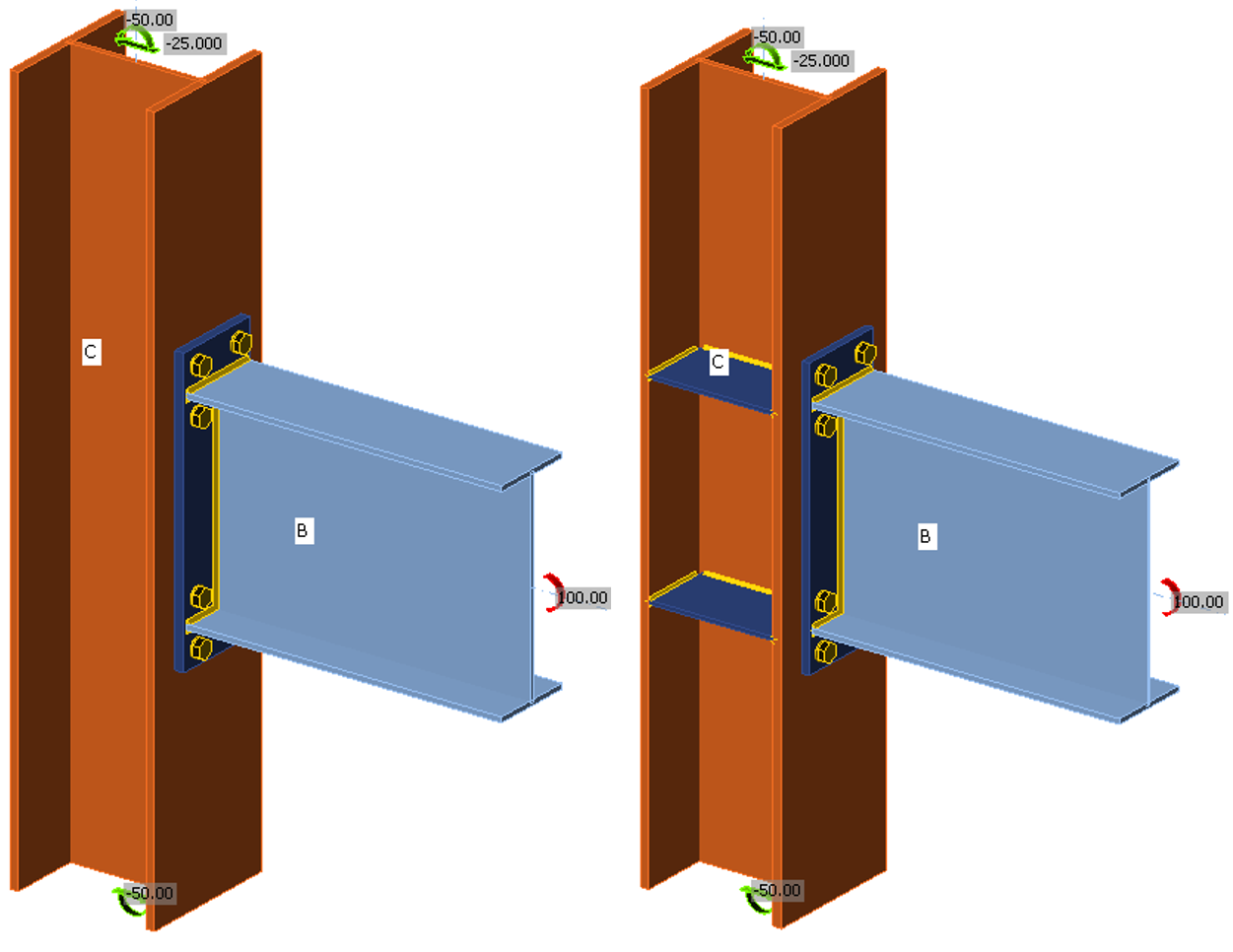
Adding stiffeners to the end plate changes the behavior of the connection. Variation of the maximum applied moment with end-plate thickness is presented in Fig. 6 for the same connections investigated previously but with end-plate stiffeners added. The IDEA StatiCa results presented in Fig. 3 for connections without stiffeners are included in Fig. 6 for reference. The stiffeners were 1/2 in. thick, 3.5 in. wide, 6.5 in. long and placed on both flanges of the beam. Plate material for the stiffeners conformed to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi).
For the traditional calculations, adding stiffeners changes the yield line pattern for the flexural strength of the end plate, decreasing the minimum thickness. However, the addition of stiffeners did not change the strength of the connection, which remained controlled by tensile rupture of the bolts, since the compression force is assumed to be centered with the flange regardless of end plate stiffness. A review of recent research has confirmed that the compression force does shift below the bottom flange with the addition of end plate stiffeners and a method of accounting for the shift in design has been proposed (Landolfo et al. 2018).
For IDEA StatiCa, adding stiffeners increased the maximum applied load. The controlling limits were the same as those presented in Table 1. The increase in maximum applied loads was greatest for end-plate thicknesses between 5/8 in. and 1 in. where bolt tension controlled, and the stiffeners helped decrease prying action and increase the lever arm of the force couple.
Fig. 6 Maximum applied moment vs end-plate thickness
The preceding analyses all used a relatively large column to ensure column limit states did not control. The column for the following analyses was smaller, a W14×109. Other aspects of the connections, including column stiffener thickness, beam, end plate, and bolts remained the same. The end plate for these analyses was unstiffened.
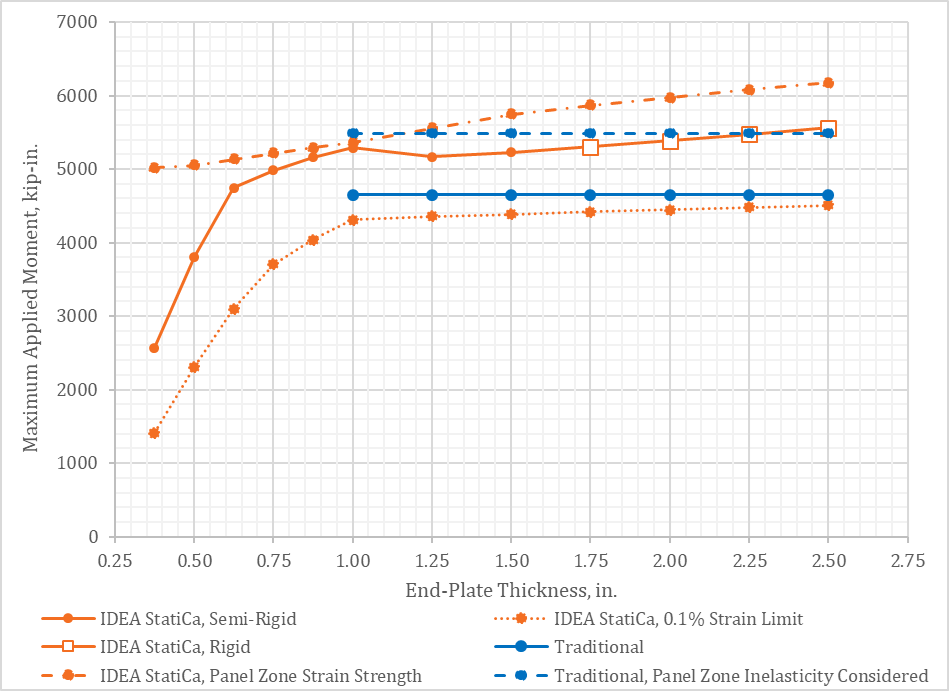
Variation of the maximum applied moment with end-plate thickness is presented in Fig. 8. The controlling limit state for each thickness is presented in Table 2. Multiple lines are plotted in this figure for both IDEA StatiCa and the traditional calculations.
For the traditional calculations, results are plotted for when the effect of inelastic panel-zone deformations on frame stability is not accounted for in the frame analysis and for when the effect is accounted for in the frame analysis. Panel-zone yielding affects overall frame stiffness and can significantly increase second-order effects. If inelasticity of the panel-zone is not accounted for in the analysis to determine required strengths of the frame, the AISC Specification (2016a) limits panel-zone behavior to the elastic range. If inelasticity of the panel-zone is accounted for when determining required strengths of the frame, additional inelastic shear strength of the panel zone is recognized.
In the case where panel-zone inelasticity is not accounted for in the analysis, panel-zone shear strength controls the strength of the connection, with a maximum applied moment of 4,649 kip-in. In the case where panel-zone inelasticity is accounted for in the analysis, tensile strength of the bolts controls the strength of the connection with a maximum applied moment of 5,490 kip-in. (note the maximum applied moment for panel-zone yielding is only slightly higher at 5,495 kip-in.).
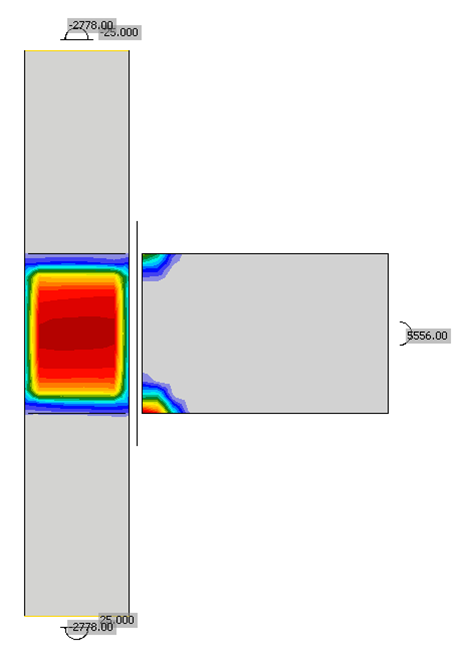
The controlling limit for IDEA StatiCa is the plastic strain limit in the end plate for very thin end plates (t ≤ 0.5 in.) and bolt tension otherwise. The maximum applied moment is greater for IDEA StatiCa than it is for the traditional calculations. The controlling limit states also differ, so additional analyses were performed to quantify the applied moment at which the plastic strain limit is reached for the column web panel zone, shown in Fig. 7 for a plate thickness of 1.25 in. These values are plotted as a dashed line in Fig. 8 (note the bolt strength limits were exceeded for these analyses).
Fig. 7 Plastic strain in panel zone for tp = 1.25 in.
IDEA StatiCa captures the panel-zone yielding limit state although with a greater strength than permitted by the AISC Specification (2016a) when the effect of inelastic panel-zone deformations on frame stability is accounted for in the analysis. Connections can be designed in IDEA StatiCa to limit yielding of the panel-zone simply by enforcing a plastic strain limit less than 5%. For example, the maximum applied load for the connection with a 1.75 in. thick end plate to have nearly elastic behavior (i.e., limit of 0.1% plastic strain) of the column web is 4,418 kip-in. which compares well to the maximum applied moment of 4,649 kip-in from the traditional calculations when the effect of inelastic panel-zone deformations on frame stability is not accounted for in the analysis.
Interestingly, prying action is identified and the connection is classified as partially restrained (semi-rigid) in IDEA StatiCa for end-plate thicknesses up to 1.5 in. The traditional calculations permit end-plate thickness as low as 1 in. with the assumption of no prying.
Fig. 8 Maximum applied moment vs. end-plate thickness
Table 2. Controlling limit state for results presented in Fig. 8
| End-Plate Thickness, in. | IDEA StatiCa | Traditional 1 | Traditional 2 |
| 0.375 | Plastic strain (end plate) | N/A | N/A |
| 0.500 | Plastic strain (end plate) | N/A | N/A |
| 0.625 | Bolt tension | N/A | N/A |
| 0.750 | Bolt tension | N/A | N/A |
| 0.875 | Bolt tension | N/A | N/A |
| 1.000 | Bolt tension | Panel zone shear | Bolt tension |
| 1.250 | Bolt tension | Panel zone shear | Bolt tension |
| 1.500 | Bolt tension | Panel zone shear | Bolt tension |
| 1.750 | Bolt tension | Panel zone shear | Bolt tension |
| 2.000 | Bolt tension | Panel zone shear | Bolt tension |
| 2.250 | Bolt tension | Panel zone shear | Bolt tension |
| 2.500 | Bolt tension | Panel zone shear | Bolt tension |
1 Effect of inelastic panel-zone deformations on frame stability not accounted for in the analysis
2 Effect of inelastic panel-zone deformations on frame stability accounted for in the analysis
3 Vertical Bolt Spacing
Thickness is not the only parameter that impacts the behavior of the end plate. As the vertical distance between the center lines of the bolts increases, so does the pitch (distance from face of beam flange to centerline of nearer bolt). Generally, the smallest possible bolt pitch is most economical (Murray and Sumner 2003), however, larger values may be necessary for constructability or other reasons.
A series of analyses is performed with varying vertical bolt spacing. For these comparisons, the beam is a W21×55, and the column is a W14×109. Both conform to ASTM A992 (Fy = 50 ksi, Fu = 65 ksi). The end plate has a depth of 28.5 in., a width of 9.0 in., a thickness of 1 in., and conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi). The connection has four bolts near each beam flange (8 total bolts) and the end plate is not stiffened. The bolts are 1 in. diameter A325 with a horizontal gage of 5.5 in. The vertical spacing between the bolts varies from 3.5 in. to 6 in. and the distance from the centerline of the bolts to the edge of the end plate varies from 2.5 in. to 1.25 in. The centroid of the bolt group was held constant. Loads were applied as described in the previous section, including 25 kips of shear in the column.
Variation of the maximum applied moment with vertical bolt spacing is presented in Fig. 9. The controlling limit state for both the traditional calculations and IDEA StatiCa was tensile rupture of the bolt for all cases. For vertical bolt spacing less than or equal to 5 in., there is close agreement between the traditional calculations and IDEA StatiCa. For larger vertical bolt spacing, the maximum applied load from IDEA StatiCa decreases. The maximum applied load from the traditional calculations is constant over the entire range. The reason for the discrepancy is prying action. The plate thickness meets the minimum thickness requirement of the traditional calculations to assume no prying action. However, prying action is observed in the IDEA StatiCa results for vertical bolt spacing of 5.5 in. and 6 in., decreasing the maximum applied moment.
Fig. 9 Maximum applied moment vs. vertical bolt spacing
4 Capacity Design
Extended end-plate moment connections are one of the connection types that are prequalified for use in special and intermediate steel moment frames (AISC 2016b). However, they are only prequalified if they meet the limitations and were designed according to the highly prescriptive procedure of AISC 358. The design criteria of AISC 358 are intended to ensure that inelastic deformation of the connection is achieved by beam yielding.
Use of IDEA StatiCa in lieu of the design procedure specified in AISC 358 is not permitted for demonstrating conformance with the requirements for beam-to-column connections for special and intermediate steel moment frames. However, IDEA StatiCa does have the capability to perform capacity design and produce comparable results.
For capacity design in IDEA StatiCa, specific elements are designated as dissipative components. The stress-strain response of these components is overridden to be based on that of the expected material strengths and to include strain hardening. Then, loads are applied corresponding to the maximum probable load effects. For the extended end-plate moment connection, the beam is the dissipative component and the maximum probable load effects are computed per AISC 358.
In this investigation, a series of connections are capacity designed according to the AISC 358 procedure and IDEA StatiCa to compare results. Note that the default resistance factors were overridden in IDEA StatiCa to match those specified in AISC 358. The beam is varied from a W18×35 to a W18×60, the column is a W14×211. All wide flange shapes conform to ASTM A992 (Fy = 50 ksi, Ry = 1.1, Fu = 65 ksi). The end plate conforms to ASTM A572 Gr. 50 (Fy = 50 ksi, Fu = 65 ksi) and has a depth of 28 in. The width of the plate was 7 in. for the W18x35, W18x40, and W18x46 beams and 8.5 in. for the W18x50, W18x55, and W18x60 beams. The thickness of the end plate was selected during the design process. A four-bolt unstiffened, 4E, configuration was used with A490 bolts. The diameter of the bolts was selected during the design process. The horizontal gage was 5.5 in., the vertical bolt spacing was 5.5 in, and the vertical distance from the centerline of the bolts to the edge of the end plate was lev = 2 in.
The applied moment and applied beam shear for each beam section are listed in Table 3. The applied beam shear was based on an assumed beam shear force resulting from gravity loads of 30 kips and beam length (between column centerlines) of 30 ft. The loads were applied at the “X-position” (i.e., the distance from the centerline of the column to assumed plastic hinge location). A shear load of 30 kips was also applied to the column. Interestingly, the plastic strains in the beam reached a maximum of approximately 10% in these analyses. However, this high level of plastic strain does not breach any limits since the beam is classified as the dissipative component.
Table 3. Applied loads for capacity design example
| Beam Section | Applied Moment, kip-in | Applied Beam Shear, kip | X-position, in |
| W18X35 | 4,206 | 55.8 | 16.70 |
| W18X40 | 4,959 | 60.4 | 16.80 |
| W18X46 | 5,737 | 65.2 | 16.90 |
| W18X50 | 6,388 | 69.2 | 16.85 |
| W18X55 | 7,084 | 73.4 | 16.90 |
| W18X60 | 7,780 | 77.7 | 16.95 |
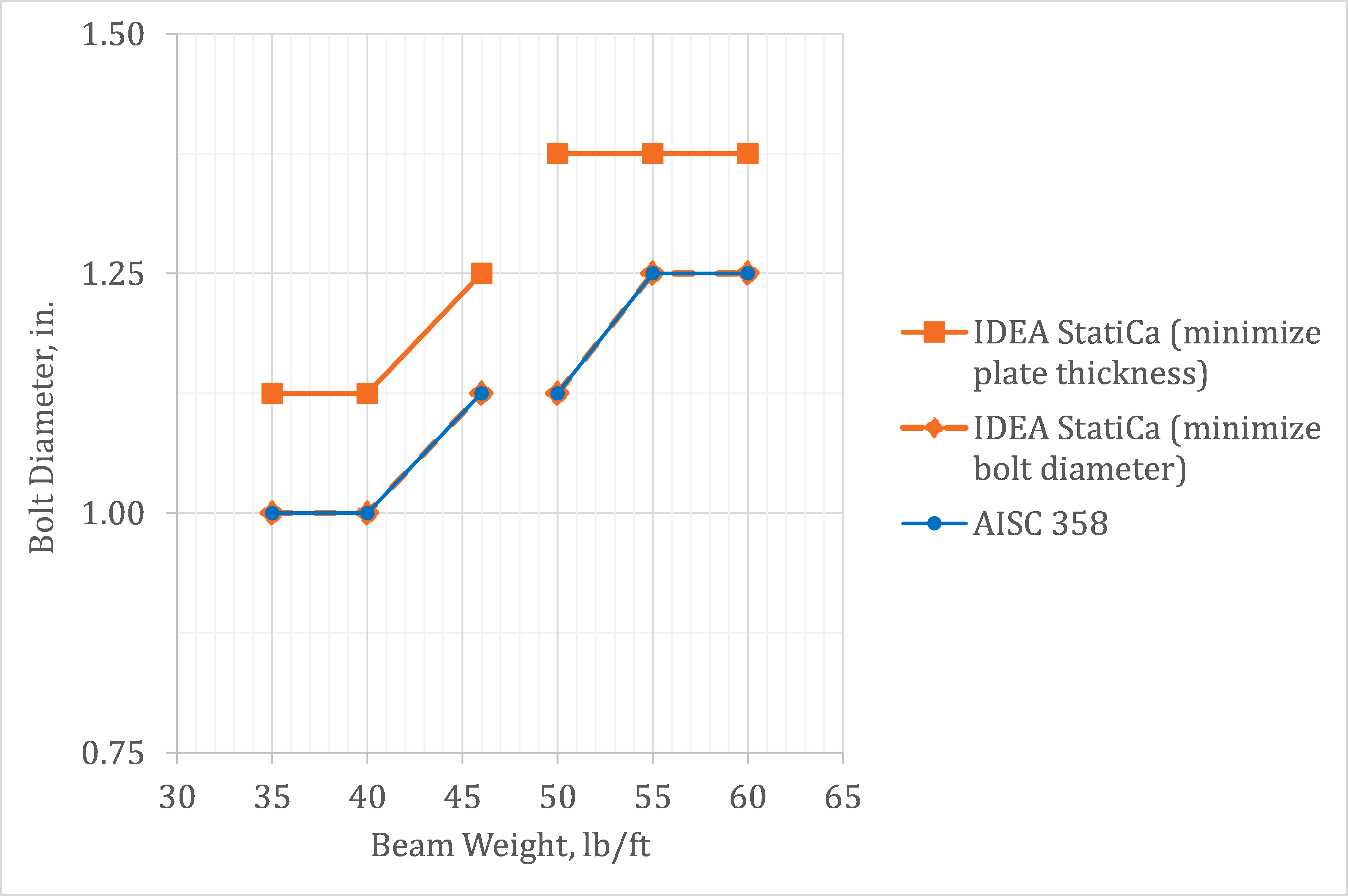
The designed end-plate thickness and bolt diameter are shown as a function of the beam weight in Fig. 10 and Fig. 11, respectively. One design is shown for each beam size for the traditional calculations since the AISC 358 procedure inhibits prying action and results in a unique efficient design. Two designs are shown for each beam size for IDEA StatiCa. With the capability of explicitly considering prying action in IDEA StatiCa, a range of efficient designs are possible depending on the relative priority of bolt diameter and plate thickness. An informal optimization was performed to determine one design where the plate thickness was minimized and another where the bolt diameter was minimized.
When bolt diameter is minimized, the resulting bolt diameter is the same between the traditional calculations and IDEA StatiCa, but the plate thickness is greater for the IDEA StatiCa design. The thicker plates are needed in IDEA StatiCa to eliminate the effect of prying action and minimize the demand on the bolts.
When the plate thickness is minimized, the resulting plate thickness for the IDEA StatiCa design is approximately the same as for the traditional calculations with some designs the same, some with one size thicker plate, and some with one size thinner plate. The bolts for the IDEA StatiCa design for these cases are larger than required per the traditional calculations due to the increased demands from prying action.
These results indicate that the modeling assumptions built into IDEA StatiCa result in a more conservative evaluation of prying action than the traditional calculations and accordingly IDEA StatiCa provides a conservative design of these two components of the extended end-plate moment connection.
Fig. 10 Plate thickness vs. beam weight
Fig. 11 Bolt diameter vs. beam weight
5 Summary
This study compared the design of extended end plate moment connections using traditional calculation methods used in US practice and IDEA StatiCa. Key observations from the study include:
- IDEA StatiCa results in available strengths for extended end plate moment connections that are similar to the traditional calculations.
- Differences in strength are mainly due to prying action and the distribution of bearing stress, both of which are addressed with simplified assumptions in the traditional calculations, but explicitly modeled in IDEA StatiCa.
- Using default parameters, web panel-zone strength from IDEA StatiCa is similar to the strength from the AISC Specification when the effect of inelastic panel-zone deformations on frame stability is accounted for in the analysis to determine required strengths. The lower strength given in the AISC Specification for when the effect of inelastic panel-zone deformations on frame stability is not accounted for in the analysis to determine required strengths can be achieved by adjusting the plastic strain limit in IDEA StatiCa.
- The capacity design capabilities of IDEA StatiCa allow for the selection of bolt diameter and plate thickness that are conservative with respect to the procedure defined in AISC 358.
6 References
AISC. (2016a). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2016b). Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2017). Steel Construction Manual, 15th Edition. American Institute of Steel Construction, Chicago, Illinois.
Dowswell, B. (2011). “A Yield Line Component Method for Bolted Flange Connections.” Engineering Journal, AISC, (2nd Quarter), 93–116.
Landolfo, R., D’Aniello, M., Costanzo, S., Tartaglia, R., Demonceau, J., Jaspart, J., Stratan, A., Jakab, D., Dubina, D., Elghazouli, A., and Bompa, D. (2018). Equaljoints PLUS – Volume with information brochures for 4 seismically qualified joints, European Convention for Constructional Steelwork (ECCS), Brussels, Belgium.
Murray, T. M. and Sumner, E. A. (2003). Extended End-Plate Moment Connections: Seismic and Wind Applications, Second Edition. Design Guide 4, American Institute of Steel Construction, Chicago, Illinois.