Chevron Brace Connection in a braced frame (AISC)
This verification example was prepared by Mahamid Mustafa in a joint project of The University of Illinois in Chicago and IDEA StatiCa.
Description
The objective of this example is verification of the component-based finite element method (CBFEM) of a chevron braced frame connection with Hollow structural sections (HSS) in tension and compression with the AISC specification design procedure. The study is prepared for the size of the braces, beam, geometry, thickness of the plate and welds. In this study, five components are examined: braces, beam flange and web, gusset plate, and welds. All components are designed according to AISC -360-16 specifications. The connection presented is taken from AISC Design Guide 29.
Verification of resistance
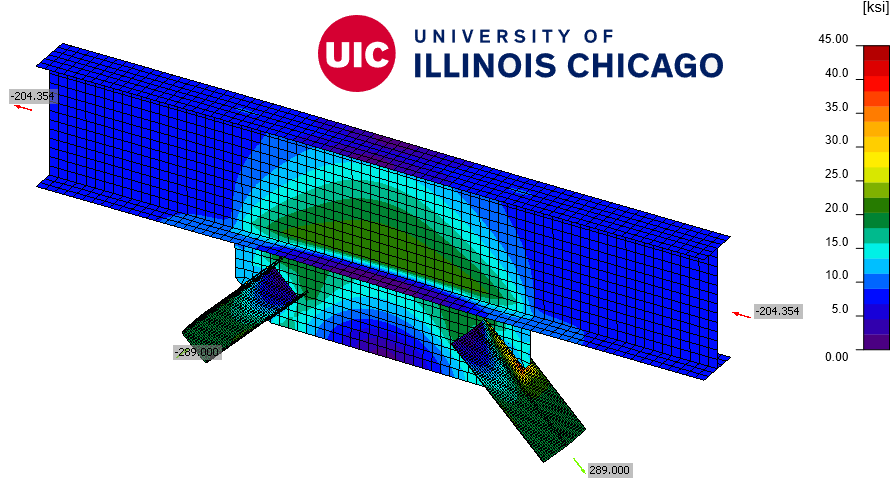
The example uses the sections and dimensions shown in Figure 1 and as follows. Braces are HSS8x8x1/2 (ASTM A500 Gr. C), beam W27x114 (ASTM A992), gusset plate ¾” (ASTM A572, Gr. 50) and ASTM E70XX weld.
Figure 1. Chevron Braced Frame Connection
The results of the analytical solution are represented by the comparison table for the different limit states shown below. The limit states that should be considered for these connections are as follows and the analysis results of these limit states are presented in Table 1.
- Weld between gusset plate and brace
- Weld between gusset plate and bottom flange of beam
- Tension yielding of brace
- Tension rupture of brace
- Shear rupture in the brace wall
- Block shear rupture
- Gusset plate for tensile yielding and shear yielding along the beam flange
- Gusset plate tension yielding on the Whitmore section
- Gusset plate for buckling on Whitmore section
- Yielding of the beam-web
- Crippling of the beam web.
Table 1. Limit States checked and compared with CBFEM
| Limit state | AISC |
| Weld between gusset plate and brace | \(\phi\)Rn =333 kips |
| Weld between gusset plate and beam bottom flange | \(\phi\)Rn =385 kips |
| Tension yielding of brace | \(\phi\)Rn =559 kips |
| Shear Rupture of brace wall | \(\phi\)Rn =583 kips |
| Brace Tension Rupture | \(\phi\)Rn =414 kips |
| Block Shear Rupture of gusset plate | \(\phi\)Rn =697 kips |
| Gusset plate tensile yielding on Whitmore section | \(\phi\)Rn =721 kips |
| Gusset plate tensile yielding and shear yielding along the beam flange | \(\phi\)Rn =45 ksi fun=15.8 ksi |
| Gusset plate for buckling on the Whitmore section | \(\phi\)Rn =671 kips |
| Gusset plate for sidesway buckling | \(\phi\)Rn =2009 kips |
| Beam web local buckling | N/A |
| Beam local web yielding | \(\phi\)Rn =2042 kips |
| Beam web shear yielding | \(\phi\)Rn =1094 kips |
| Beam Web crippling | \(\phi\)Rn =1311 kips |
The governing component of this connection is the weld between the gusset plate and the brace (\(\phi\)Rn = 333 kips > Pu = 289 kips). The utilization of this weld is 87%. The next critical check is brace tension rupture with the load resistance of \(\phi\)Rn =414 kips > Pu = 289 kips (Utilization 70%).
Resistance by CBFEM
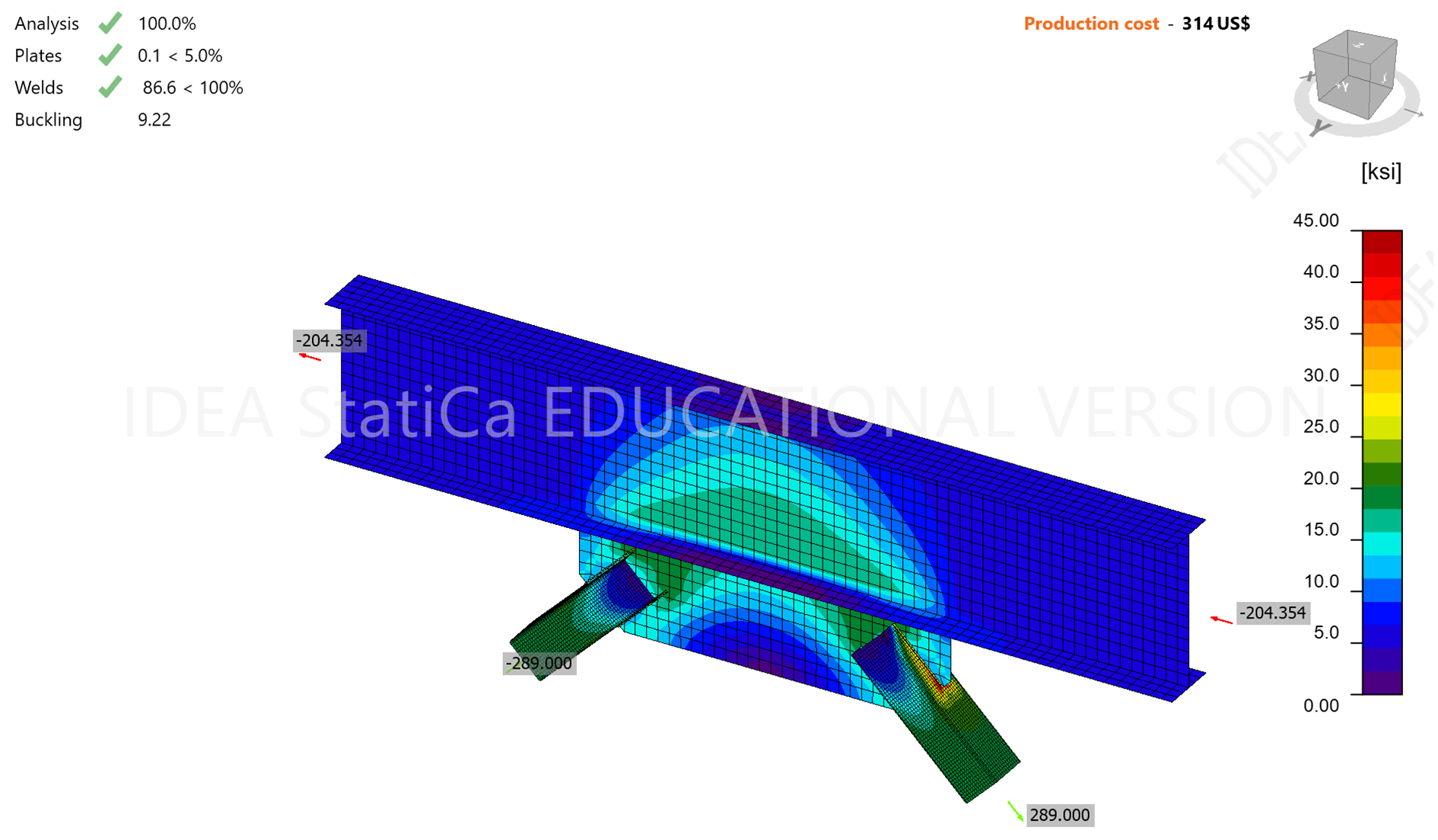
The overall check of the connection is verified as shown in Figures 2–4. The check shows that the connection works according to the CBFEM. Failure in members and plates due to yielding and rupture limit states is measured based on 5% plastic strain limit. The figure below shows that the plastic strain is 0.1% which is well below the 5% plastic strain limit. The connection presented is a welded connection. The weld shear limit state is usually accurate when compared with the AISC specification procedure. CBFEM uses the AISC 360-16 provisions of Chapter J to check the weld strength. It can be seen that the weld check utilization is 86.6%. The analysis is materially nonlinear, and it should not rely only upon utilization. By overloading the basic model from 333 kips to 334 kips in each brace, the load resistance is revealed – the weld just barely holds at 333 kips and fails at 334 kips. Both AISC and CBFEM detect the weld as the governing component and provide the same load resistance.
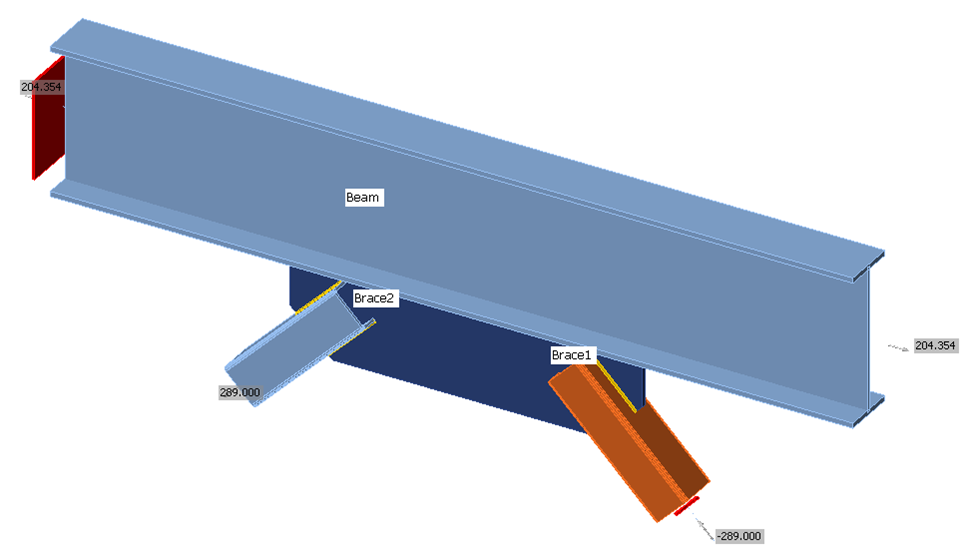
Figure 2: Design model
Figure 3. Overall solution of the connection – stresses
Figure 4. Overall solution of the connection – plastic strains
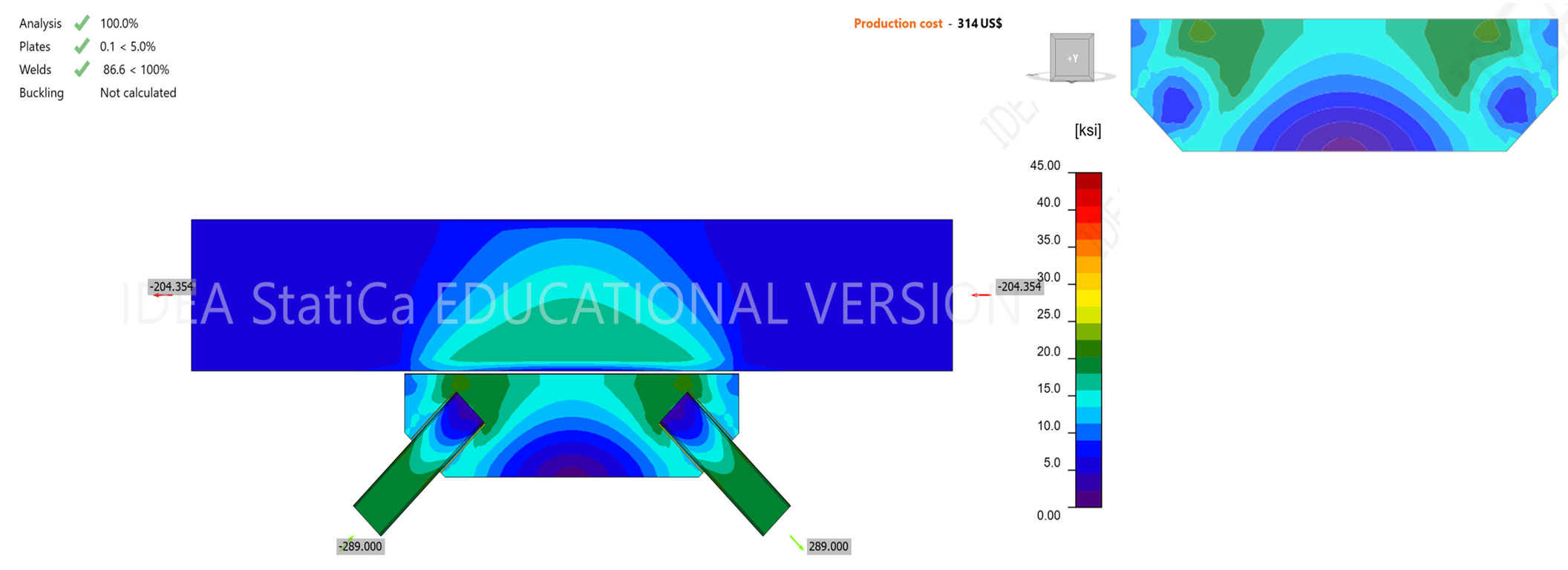
For the gusset plate tensile yielding and shear yielding along the beam flange, the AISC 360-16 procedure requires comparing the combined yielding and shear stresses to the permitted stress (\(\phi\)Rn = \(\phi\)Fy=0.9(50 ksi)=45 ksi). The results of the comparison are shown in Table 1 and are in agreement. Figure 5 shows the stress distribution in the overall connection and in the gusset plate.
Figure 5. Gusset plate for tensile yielding and shear yielding along the beam flange
Buckling of the gusset plate required by AISC can be checked by a buckling multiplier using the CBFEM as it is the only measure. It is hard to differentiate between the buckling resistances of various connection parts, e.g. buckling of gusset plate on the Whitmore section or gusset plate sidesway buckling. The first buckling mode shape includes the gusset plate and the beam web near the compressed brace. The buckling factor for internal plates higher than 3 is considered to be safe.
Figure 6. First buckling mode shape with the factor of 7.85
Parametric study
To verify the resistance of other components and the ability of CBFEM to capture all the failure modes, the parametric study is prepared by varying plate thicknesses and weld size.
Modification 1 – fillet welds at braces changed to butt welds:
The governing failure mode of the basic model is the failure of fillet welds at braces. Therefore, these fillet welds are changed in the model to full-penetration butt welds. The load at braces may be increased to 479 kips. At this load, the fillet welds between the gusset plate and the beam are utilized at 100%; see Figure 6. Hand calculation provides resistance 430 kips. CBFEM provides higher resistance by 10%.
Figure 7. Modified model with butt welds between braces and gusset plate
Modification 2 – all fillet welds changed to butt welds:
The second modification avoids the failure mode of fillet welds between the gusset plate and the brace. Plastic limit strain limit check is used to simulate the following checks in hand calculation: Tension yielding of the brace: \(\phi\)Rn = 559 kips, Shear Rupture of brace wall: \(\phi\)Rn = 583 kips, and Brace Tension Rupture: \(\phi\)Rn = 414 kips. The plastic strains start at the net section of the brace and propagate to the gross area as the load increases. The load can be increased to 540 kips, when the plates of both braces just barely satisfy the plastic strain limit check. This load is in agreement with the AISC capacities shown in Table 1 for tension yielding and shear rupture. The tension rupture per AISC 360 specifications is less than what was obtained from CBFEM, and this is due to the shear lag factor, U, which is equal to 0.75 in this case and as required by Table D3.1 case 6 (AISC 360-16); the shear lag factor is multiplied by the net area of the brace. The effect of shear lag is apparent in Figure 7. Without the shear lag factor, the tension rupture capacity of the section is 552 kips per AISC which is more in line with CBFEM capacity. According to the recent findings (Dowswell, 2021), the shear lag factor for slotted rectangular HSS members in AISC 360-16 is overly conservative and the results of IDEA StatiCa are more realistic.
Figure 8. Plastic strain at model with butt welds only
Modification 3 – all butt welds and gusset plate thickness lowered to 3/8 in:
This modification is used to investigate failure modes connected to the gusset plate. The plastic strain limit is exceeded at load 400 kips in each brace. This check simulates Block Shear Rupture of gusset plate, Gusset plate tensile yielding on Whitmore section, Gusset plate tensile yielding and shear yielding along the beam flange. According to CBFEM, Gusset plate tensile yielding and shear yielding along the beam flange is the governing failure mode, and the block shear rupture of gusset plate will soon follow because the significant plastic strain is along the full length of the braces.
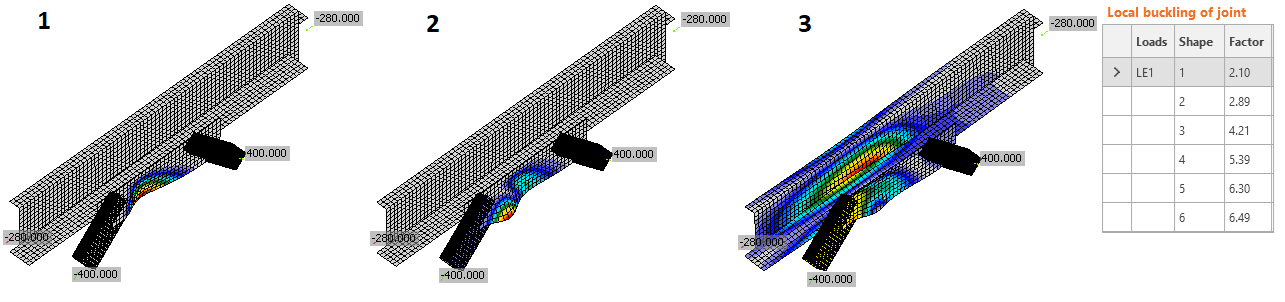
The AISC procedure predicts tensile yielding of the gusset plate at Whitmore section followed by block shear in the gusset plate. Since CBFEM uses von Mises stresses which include both normal and shear stresses, the prediction by CBFEM is accurate. For buckling analysis of the gusset plate, both AISC and CBFEM predicted the buckling in the 3/8” plate. The AISC buckling capacity for the gusset plate is 359 kips, where the applied load is 400 kips.
Figure 9. Plastic strain at the model with thin gusset plate
Figure 10. First three buckling mode shapes of model with thin gusset plate
Beam web local and shear yielding have a very large load resistance compared to the applied load. Almost all limit states in this connection would occur before these two limit states, which typically do not control the design. These limit states are checked by 5% limit strain in the beam.
Beam web crippling is a buckling state that would occur after yielding; therefore, linear buckling analysis is not perfectly ideal. In CBFEM, using geometrically linear analysis without imperfections, the buckling factor limit is the only way to capture this failure mode.
A separate model was not created specifically for these failure modes to govern.
Summary
It can be concluded that the CBFEM is capable of predicting the actual behavior and failure mode of chevron braced frame connections similar to the one presented herein.
The various limit states were investigated carefully by performing a parametric study which resulted in obtaining the capacity for each limit state using CBFEM. The weld capacity between the braces and the gusset based on AISC 360 specifications matches what is obtained by CBFEM, where the weld between the gusset plate and the beam the capacity per AISC is less than the capacity per CBFEM by 10%. The plate limit states including yielding, rupture are based on 5% plastic strain limit in CBFEM; for these limit states, the difference between the AISC and CBFEM is within 10%. The buckling limit state was investigated per AISC and per CBFEM; in the connection investigated, buckling was not a governing limit state. To investigate buckling, a 3/8” plate was investigated and in both AISC procedure and CBFEM, buckling of the plate was observed in both methods.
Benchmark case
Input
Beam cross-section
- W27X114
- Steel ASTM A992
Braces cross-section
- HSS 8X8X1/2
- Steel ASTM A500 Gr. C
Gusset plate
- Thickness 3/4 in.
- Steel ASTM A572 Gr. 50
Loading
- Axial force N = ±289 kips
Output
- Weld 86.6%
- Plastic strain 0.1% < 5%
- Buckling factor 7.85
References
AISC. (2016). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2017). Steel Construction Manual, 15th Edition. American Institute of Steel Construction, Chicago, Illinois.
AISC. (2015). Design Guide 29, Vertical Bracing Connections-Analysis and Design, American Institute of Steel Construction, Chicago, Illinois.
Dowswell, Bo (2021). "Analysis of the Shear Lag Factor for Slotted Rectangular HSS Members," Engineering Journal, American Institute of Steel Construction, Third Quarter, pp. 171-202.
Attached Downloads
- Example 2 - Chevron Brace.pdf (PDF, 1.7 MB)