Description
The objective of this chapter is verification of component-based finite element method (CBFEM) of T-stubs connected with two bolts loaded in tension with component method (CM) and research FEM model (RM) created in Midas FEA software; see (Gödrich et al. 2019).
Analytical model
Welded T-stub and bolt in tension are components examined in the study. Both components are designed according to EN 1993-1-8:2005. The welds are designed not to be the weakest component. Effective lengths for circular and noncircular failures are considered according to EN 1993-1-8:2005 cl. 6.2.6. Only tension loads are considered. Three modes of collapse according to EN 1993-1-8:2005 cl. 6.2.4.1 are considered: 1. mode with full yielding of the flange, 2. mode with two yield lines by web and rupture of the bolts, and 3. mode for rupture of the bolts; see Fig. 5.1.1. Bolts are designed according to cl. 3.6.1 in EN 1993-1-8:2005. Design resistance considers punching shear resistance and rupture of the bolt.
Fig. 5.1.1 Collapse modes of T-stub
Design numerical model
T-stub is modeled by 4-nodes shell elements as described in Chapter 3 and summarised further. Every node has 6 degrees of freedom. Deformations of the element consist of membrane and flexural contributions. Nonlinear elastic-plastic material status is investigated in each layer of integration point. Assessment is based on the maximum strain given according to EN 1993‑1‑5:2006 by value of 5 %. Bolts are divided into three sub-components. The first is the bolt shank, which is modeled as a nonlinear spring and caries tension only. The second sub-component transmits tensile force into the flanges. The third sub-component solves shear transmission.
Research numerical model
In cases where the CBFEM gives higher resistance, initial stiffness, or deformation capacity, research FEM model (RM) from brick elements validated on experiments (Gödrich et al. 2013) is used to verify the CBFEM model. RM is created in Midas FEA software of hexahedral and octahedral solid elements, see Fig. 5.1.2 Mesh sensitivity study was provided to reach proper results in adequate time. Numerical model of the bolts is based on the model by (Wu et al. 2012). The nominal diameter is considered in the shank, and the effective core diameter is considered in the threaded part. Washers are coupled with the head and nut. Deformation caused by stripping of the threads in thread–nut contact area is modeled using interface elements. Interface elements are unable to transfer tensile stresses. Contact elements allowing the transmission of pressure and friction are used between washers and flanges of the T-stub. One-quarter of the sample was modeled using the symmetry.
Fig. 5.1.2 Research FEM model
Fig. 5.1.3 Geometry of the T-stubs
Range of validity
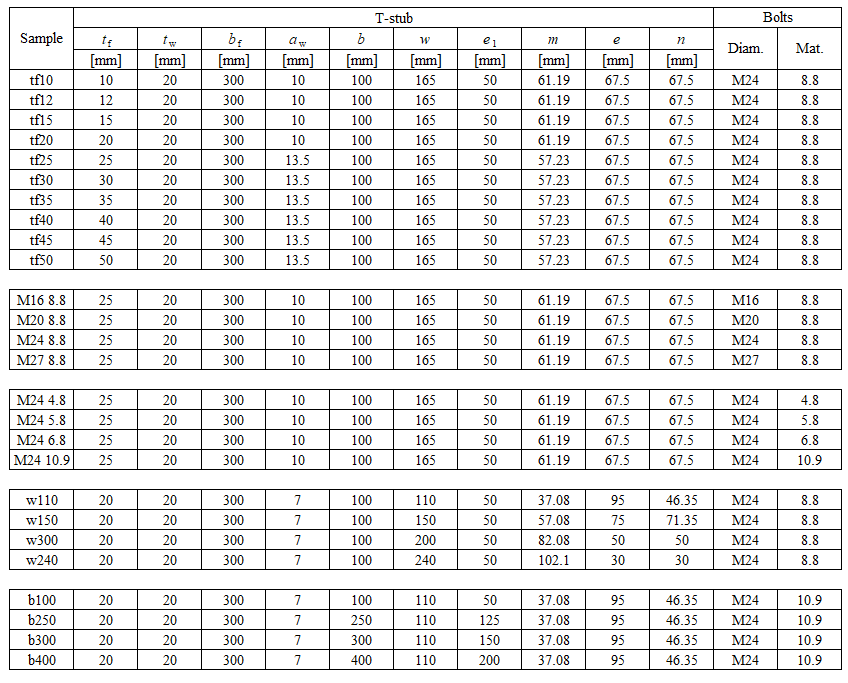
CBFEM was verified for the selected typical T-stub geometries. The minimal thickness of the flange is 8 mm. Maximal distance of the bolts to bolt diameter is limited by p/db ≤ 20. The distance of the bolt line to the web is limited to m/db ≤ 5. Overview of the considered samples with steel plates of S235: fy = 235 MPa, fu = 360 MPa, E = Ebolt = 210 GPa is shown in the Tab. 5.1.1 and in Fig. 5.1.3.
Tab. 5.1.1 Overview of the considered samples of T stubs
| Sample | T-stub | Bolts | ||||||||||
| tf | tw | bf | aw | b | w | e1 | m | e | n | Diam. | Mat. | |
| [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | |||
| tf10 | 10 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 8.8 |
| tf12 | 12 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 8.8 |
| tf15 | 15 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 8.8 |
| tf20 | 20 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 8.8 |
| tf25 | 25 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| tf30 | 30 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| tf35 | 35 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| tf40 | 40 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| tf45 | 45 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| tf50 | 50 | 20 | 300 | 13,5 | 100 | 165 | 50 | 57,23 | 67,5 | 67,5 | M24 | 8.8 |
| M16 8.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M16 | 8.8 |
| M20 8.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M20 | 8.8 |
| M24 8.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 8.8 |
| M27 8.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M27 | 8.8 |
| M24 4.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 4.8 |
| M24 5.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 5.8 |
| M24 6.8 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 6.8 |
| M24 10.9 | 25 | 20 | 300 | 10 | 100 | 165 | 50 | 61,19 | 67,5 | 67,5 | M24 | 10.9 |
| w110 | 20 | 20 | 300 | 7 | 100 | 110 | 50 | 37,08 | 95 | 46,35 | M24 | 8.8 |
| w150 | 20 | 20 | 300 | 7 | 100 | 150 | 50 | 57,08 | 75 | 71,35 | M24 | 8.8 |
| w200 | 20 | 20 | 300 | 7 | 100 | 200 | 50 | 82,08 | 50 | 50 | M24 | 8.8 |
| w240 | 20 | 20 | 300 | 7 | 100 | 240 | 50 | 102,1 | 30 | 30 | M24 | 8.8 |
| b100 | 20 | 20 | 300 | 7 | 100 | 110 | 50 | 37,08 | 95 | 46,35 | M24 | 10.9 |
| b250 | 20 | 20 | 300 | 7 | 250 | 110 | 125 | 37,08 | 95 | 46,35 | M24 | 10.9 |
| b300 | 20 | 20 | 300 | 7 | 300 | 110 | 150 | 37,08 | 95 | 46,35 | M24 | 10.9 |
| b400 | 20 | 20 | 300 | 7 | 400 | 110 | 200 | 37,08 | 95 | 46,35 | M24 | 10.9 |
Global behavior
Comparison of the global behavior of the T-stub described by force–deformation diagrams for all design procedures was prepared. Attention was focused on the main characteristics: initial stiffness, design resistance, and deformation capacity. Sample tf20 was chosen to present as a reference; see Fig. 5.1.4 and Tab. 5.1.2. CM generally gives higher initial stiffness compared to CBFEM and RM. In all cases, RM gives the highest design resistance, as shown in chapter 6. Deformation capacity is also compared. Deformation capacity of T-stub was calculated according to (Beg et al. 2004). RM does not consider cracking of the material, so the prediction of deformation capacity is limited.
Fig. 5.1.4 Force–deformation diagram
Tab. 5.1.2 Global behavior overview
| CM | CBFEM | RM | CM/CBFEM | RM/CBFEM | ||
| Initial stiffness | [kN/m] | 484727 | 181818 | 197400 | 2,67 | 1,09 |
| Design resistance | [kNm] | 174 | 165 | 268,8 | 1,05 | 1,63 |
| Deformation capacity | [mm] | 24,5 | 6,5 | - | 3,77 | - |
Verification of resistance
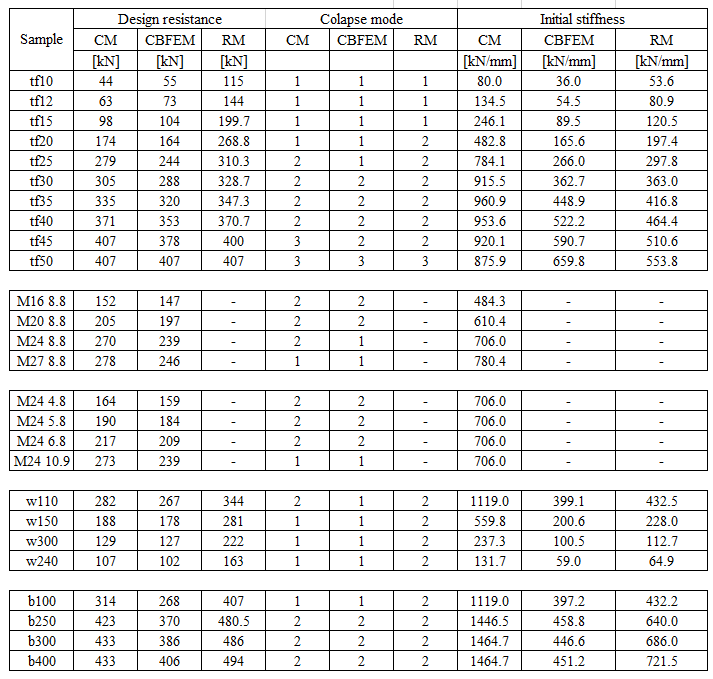
Design resistances calculated by CBFEM were compared with the results of CM and RM in the next step. The comparison was focused on the deformation capacity and determination of the collapse mode too. All results are ordered in Tab. 5.1.3. The study was performed for five parameters: thickness of the flange, bolt size, bolt material, bolt space, and T-stub width.
Tab. 5.1.3 Global behavior overview
| Sample | CM | CBFEM | RM | ||||||
| Design res. | Collapse mode | Initial stiffness | Design res. | Collapse mode | Initial stiffness | Design res. | Collapse mode | Initial stiffness | |
| [kN] | [kN/mm] | [kN] | [kN/mm] | [kN] | [kN/mm] | ||||
| Parameter: | Thickness of the flange | ||||||||
| tf10 | 44 | 1 | 80,0 | 63 | 1 | 39,4 | 115 | 1 | 53,6 |
| tf12 | 63 | 1 | 134,6 | 78 | 1 | 58,8 | 144 | 1 | 80,9 |
| tf15 | 98 | 1 | 246,6 | 105 | 1 | 97,1 | 199,7 | 1 | 120,5 |
| tf20 | 174 | 1 | 484,7 | 165 | 1 | 181,8 | 268,8 | 2 | 197,4 |
| tf25 | 279 | 2 | 789,3 | 238 | 1 | 285,7 | 310,3 | 2 | 297,8 |
| tf30 | 305 | 2 | 922,6 | 288 | 2 | 392,2 | 328,7 | 2 | 363 |
| tf35 | 335 | 2 | 968,8 | 320 | 2 | 485,4 | 347,3 | 2 | 416,8 |
| tf40 | 371 | 2 | 961,3 | 344 | 2 | 573,8 | 370,7 | 2 | 464,4 |
| tf45 | 407 | 3 | 927,3 | 385 | 2 | 654,2 | 400 | 2 | 510,6 |
| tf50 | 407 | 3 | 882,4 | 412 | 3 | 736,8 | 407 | 3 | 553,8 |
| Parameter: | Bolt size | ||||||||
| M16 8.8 | 152 | 2 | 486,6 | 150 | 2 | - | - | - | - |
| M20 8.8 | 205 | 2 | 612,7 | 200 | 2 | - | - | - | - |
| M24 8.8 | 270 | 2 | 710,2 | 238 | 1 | - | - | - | - |
| M27 8.8 | 278 | 1 | 782,4 | 250 | 1 | - | - | - | - |
| Parameter: | Bolt material | ||||||||
| M24 4.8 | 164 | 2 | 710,2 | 163 | 2 | - | - | - | - |
| M24 5.8 | 190 | 2 | 710,2 | 186 | 2 | - | - | - | - |
| M24 6.8 | 217 | 2 | 693,6 | 210 | 2 | - | - | - | - |
| M24 10.9 | 273 | 1 | 677,8 | 253 | 1 | - | - | - | - |
| Parameter: | Bolt spacing | ||||||||
| w110 | 282 | 2 | 1129,7 | 262 | 1 | 465,1 | 344 | 2 | 432,5 |
| w150 | 188 | 1 | 562,4 | 184 | 1 | 229,0 | 281 | 2 | 228,0 |
| w200 | 129 | 1 | 237,8 | 133 | 1 | 111,9 | 222 | 2 | 112,7 |
| w240 | 107 | 1 | 131,9 | 109 | 1 | 66,1 | 162,7 | 2 | 64,9 |
| Parameter: | T-stub width | ||||||||
| b100 | 314 | 1 | 1129,7 | 285 | 1 | 463,0 | 407 | 2 | 432,2 |
| b250 | 423 | 2 | 1443,5 | 448 | 2 | 534,4 | 480,5 | 2 | 640,0 |
| b300 | 433 | 2 | 1443,5 | 466 | 2 | 534,4 | 486 | 2 | 686,0 |
| b400 | 433 | 2 | 1443,5 | 492 | 2 | 538,5 | 494 | 2 | 721,5 |
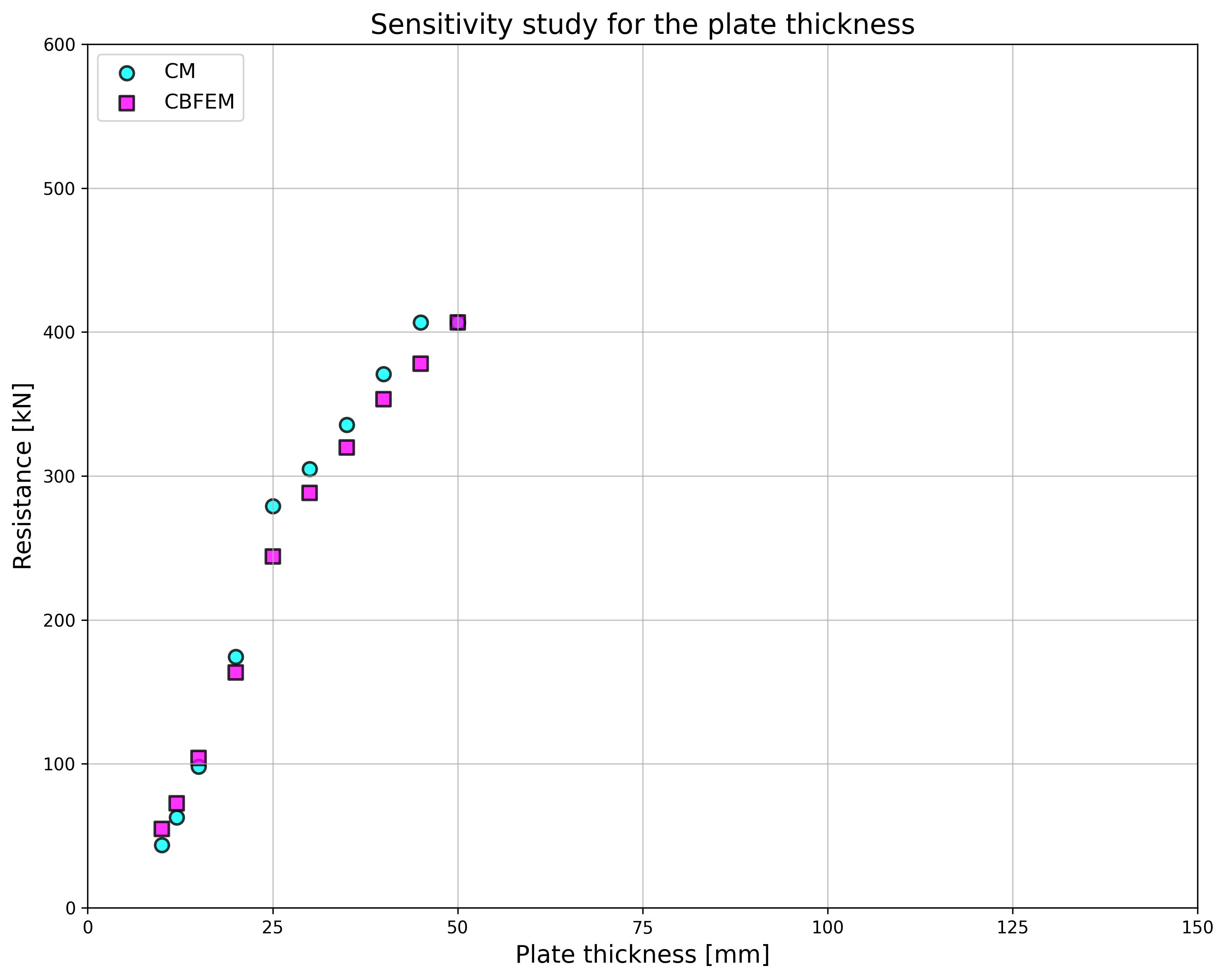
Fig. 5.1.5 Sensitivity study of flange thickness
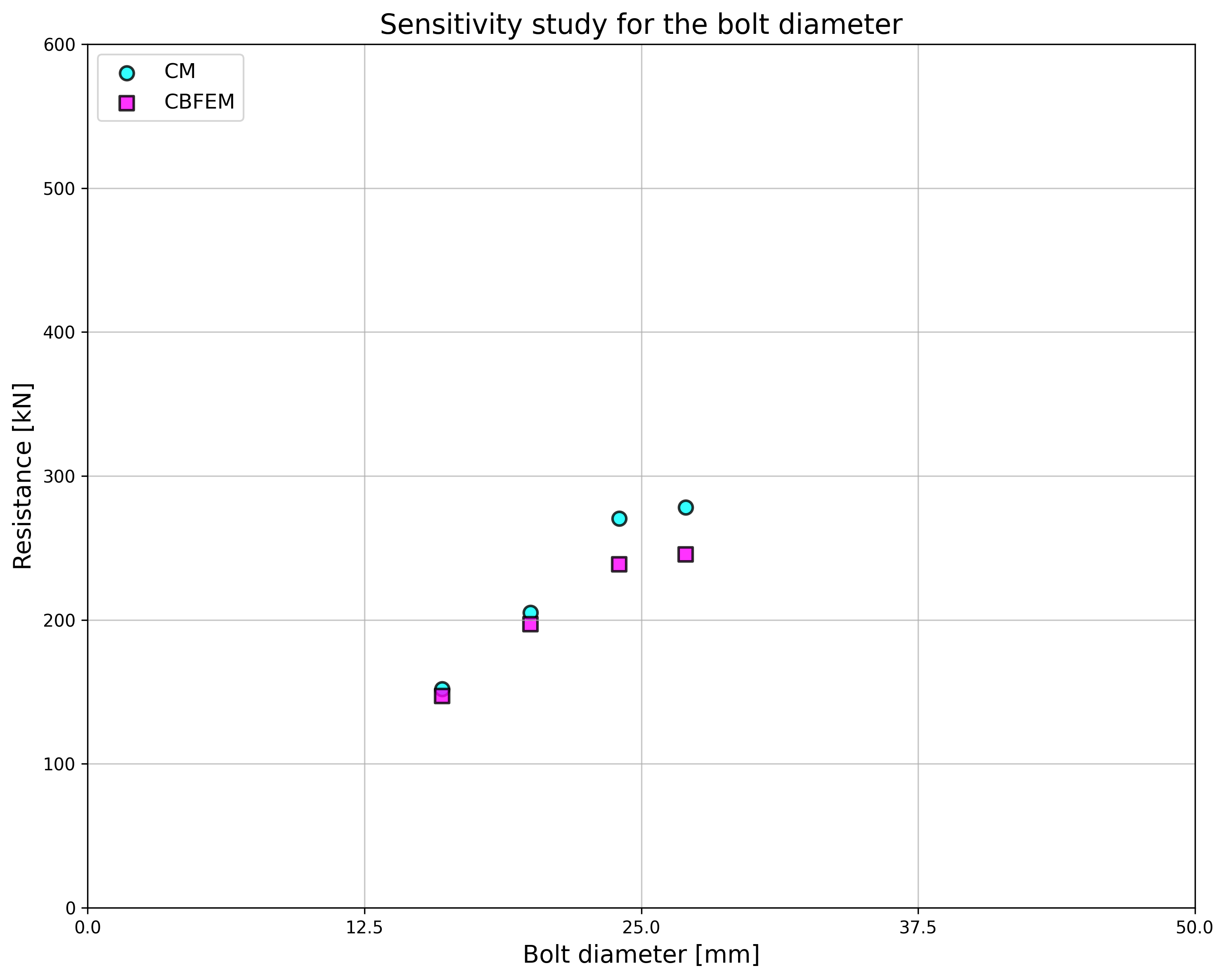
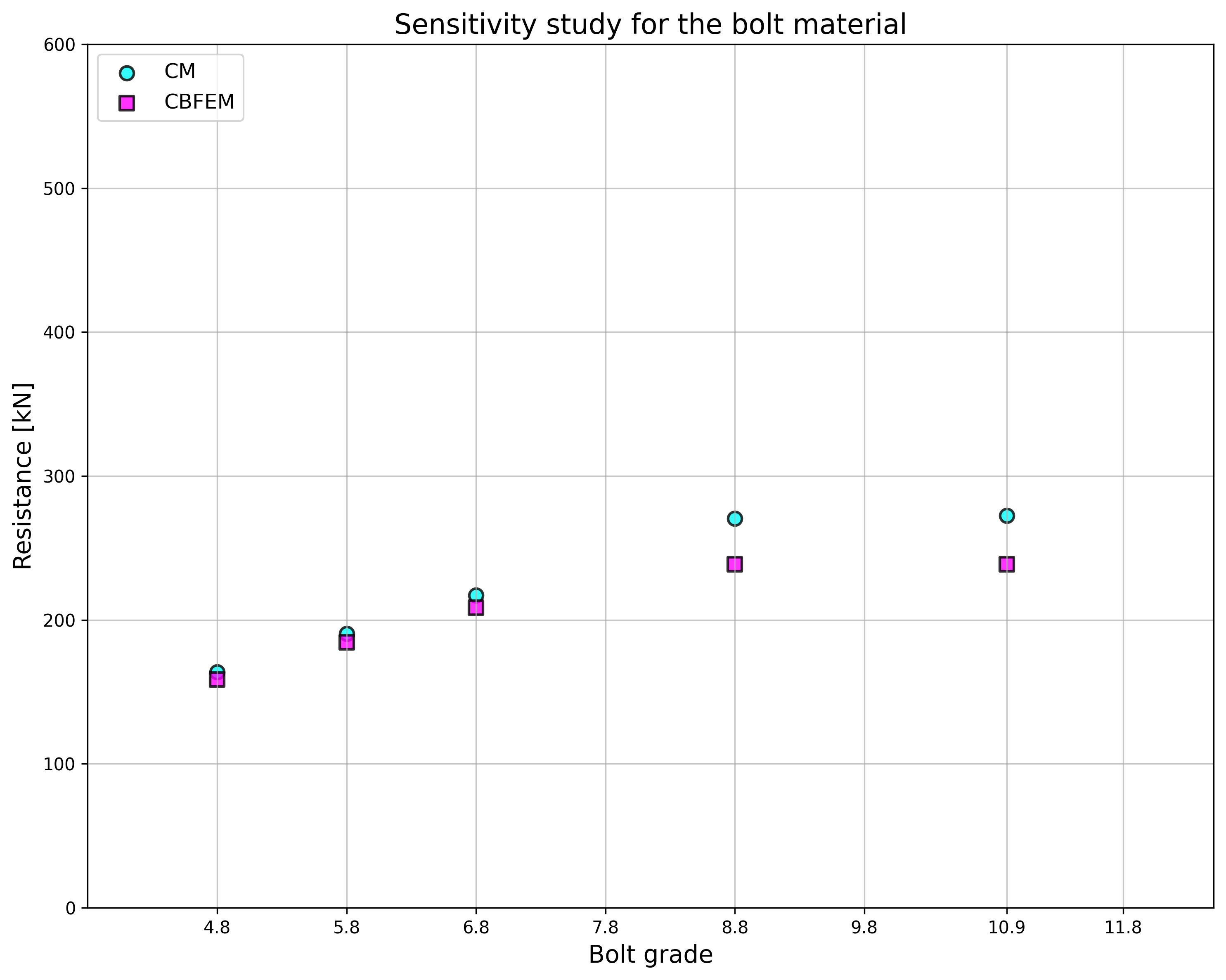
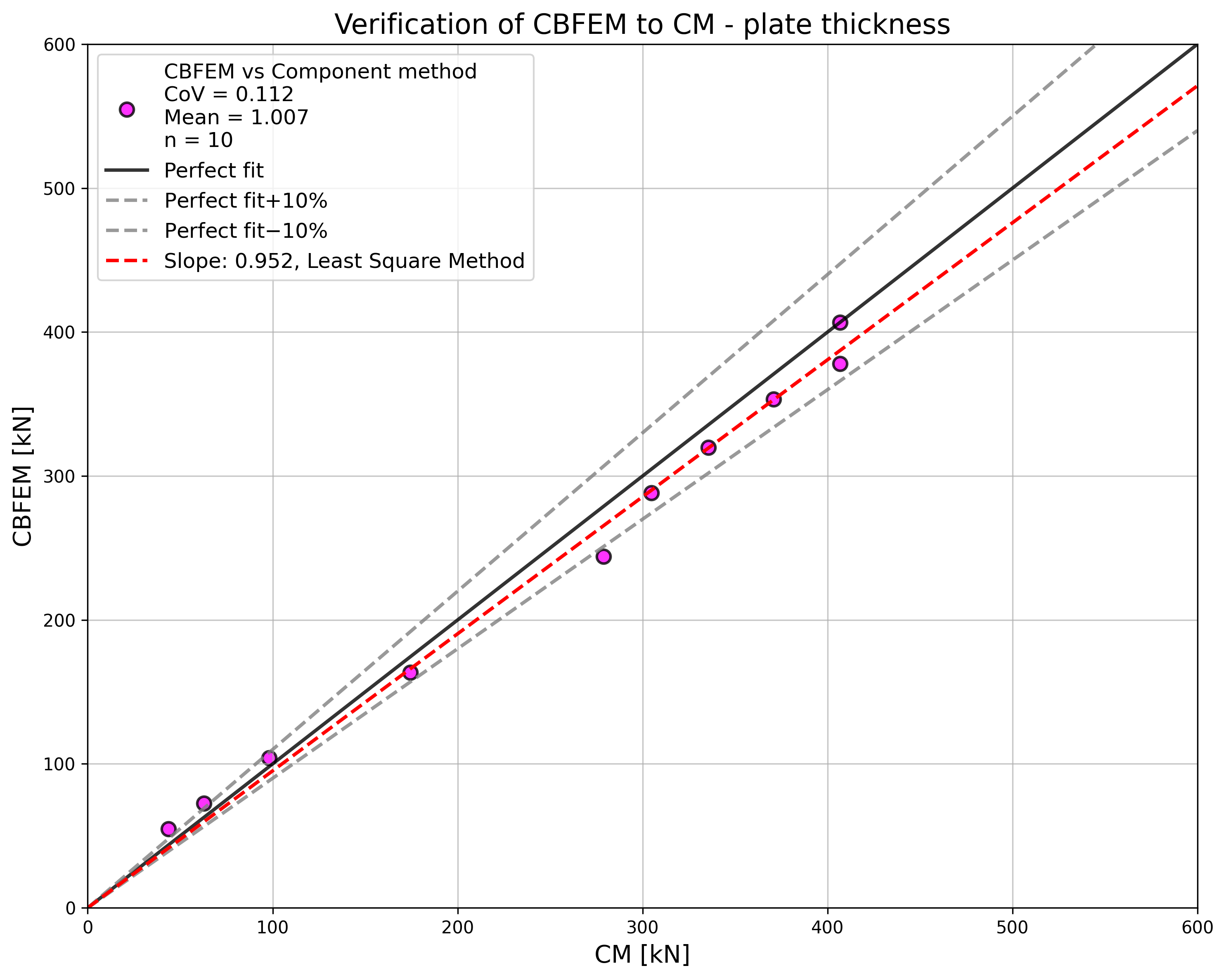
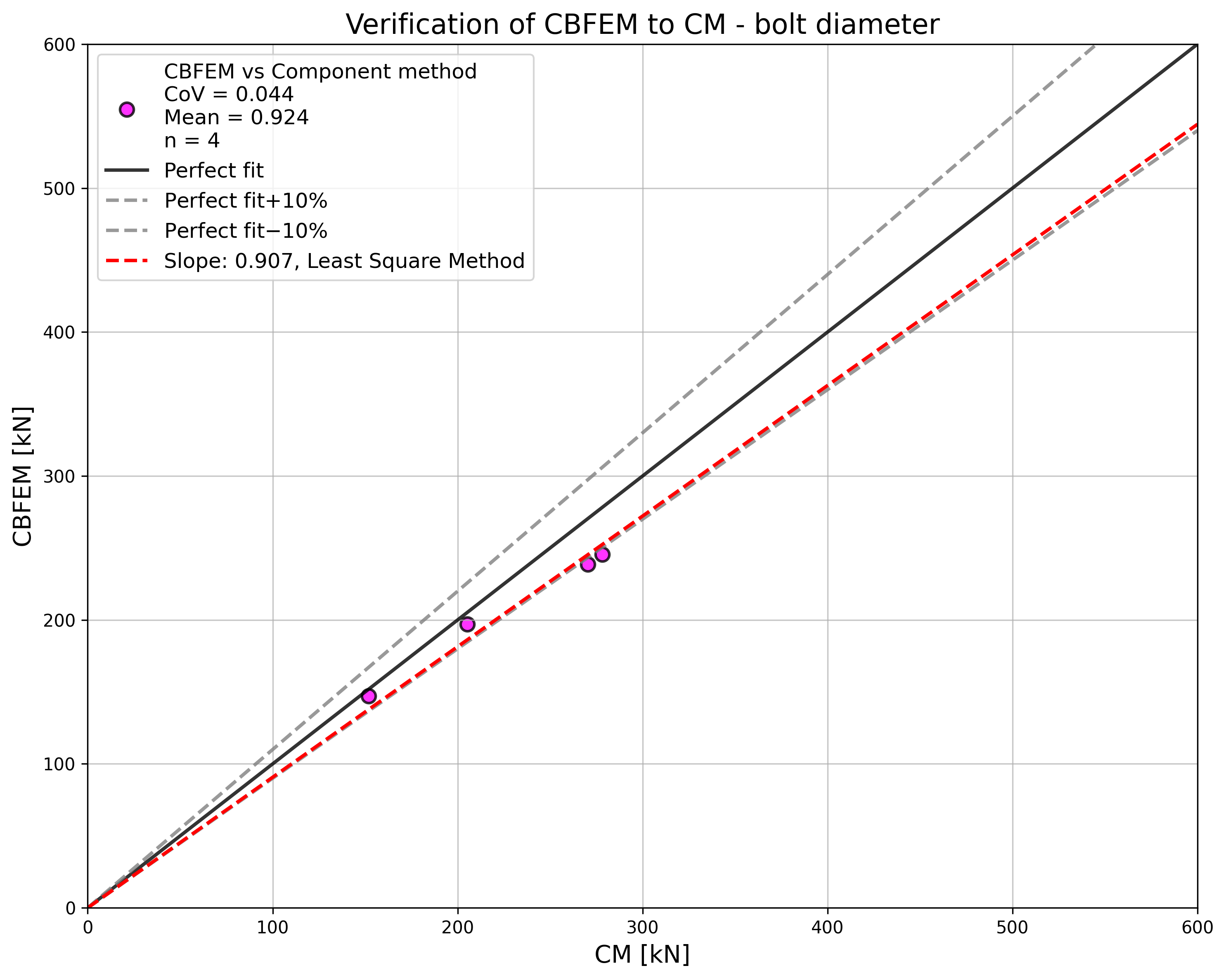
The sensitivity study of thickness of the flange shows higher resistance according to CBFEM compared to CM for samples with flange thicknesses up to 20 mm. RM gives even higher resistance for these samples; see Fig. 5.1.5. Higher resistance of both numerical models is explained by neglecting membrane effect in CM. In case of the bolt diameter and bolt material (see Fig. 5.1.6 and Fig. 5.1.7, respectively), the results of CBFEM correspond to these of CM. Due to a good agreement of both methods, the results of RM are not required.
Fig. 5.1.6 Sensitivity study of the bolt size
Fig. 5.1.7 Sensitivity study of the bolt material
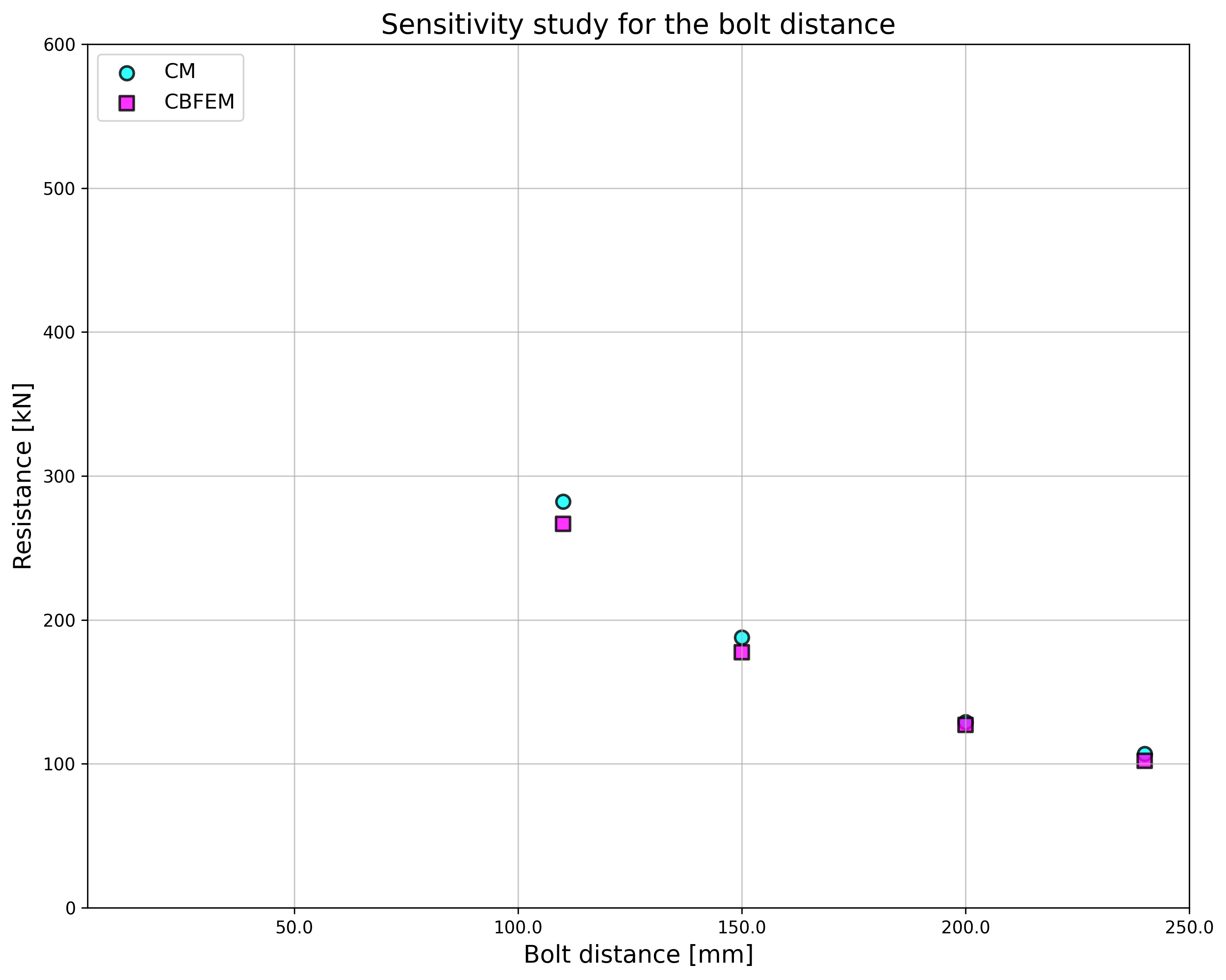
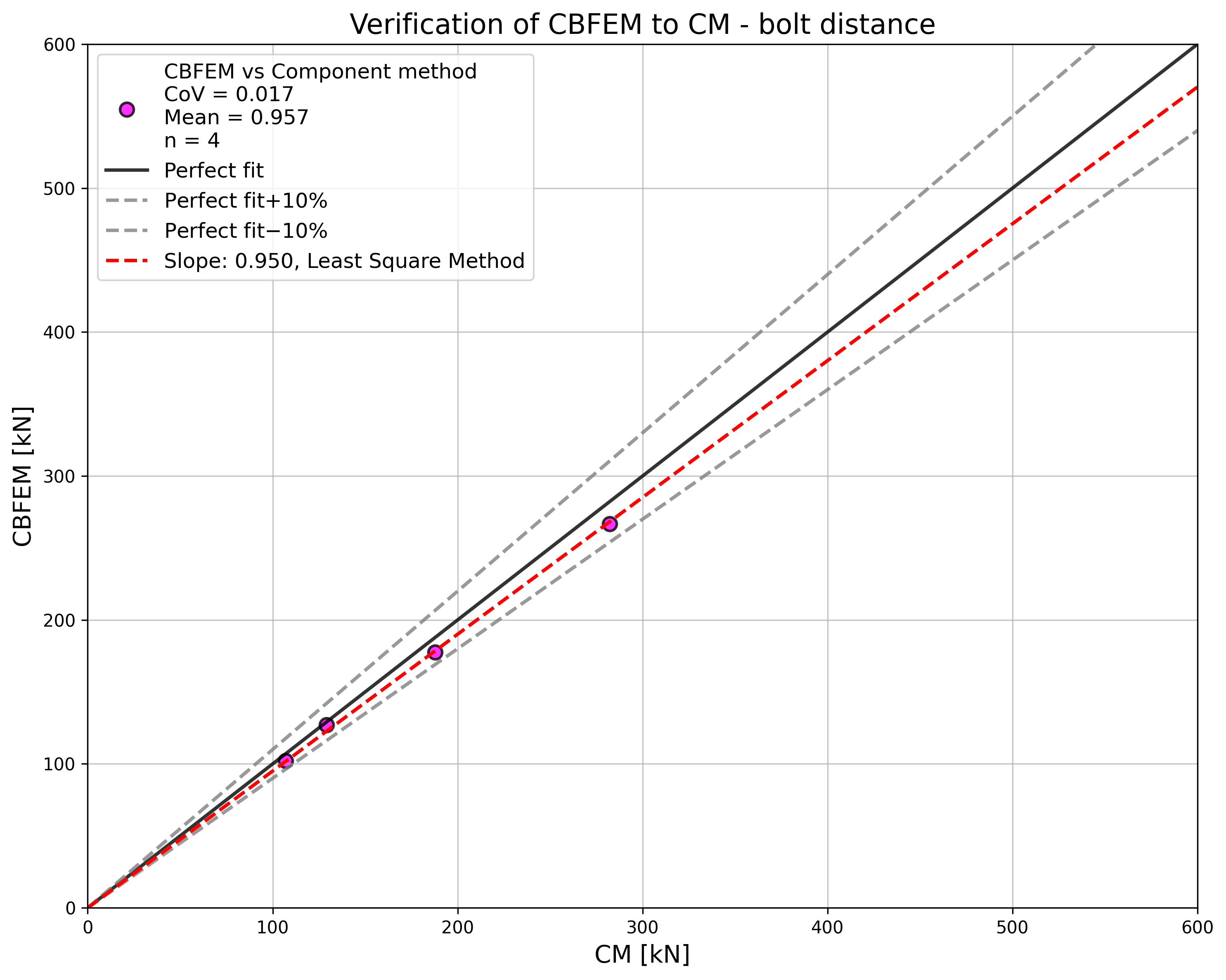
In the case of the bolt distances, the results of CBFEM and CM show generally good agreement; see Fig. 5.1.8. With an increase in bolt spacing, CBFEM gives slightly higher resistance compared to CM. For that reason, the results of RM are also shown. RM gives the highest resistance in all cases.
Fig. 5.1.8 Sensitivity study of the bolt distance
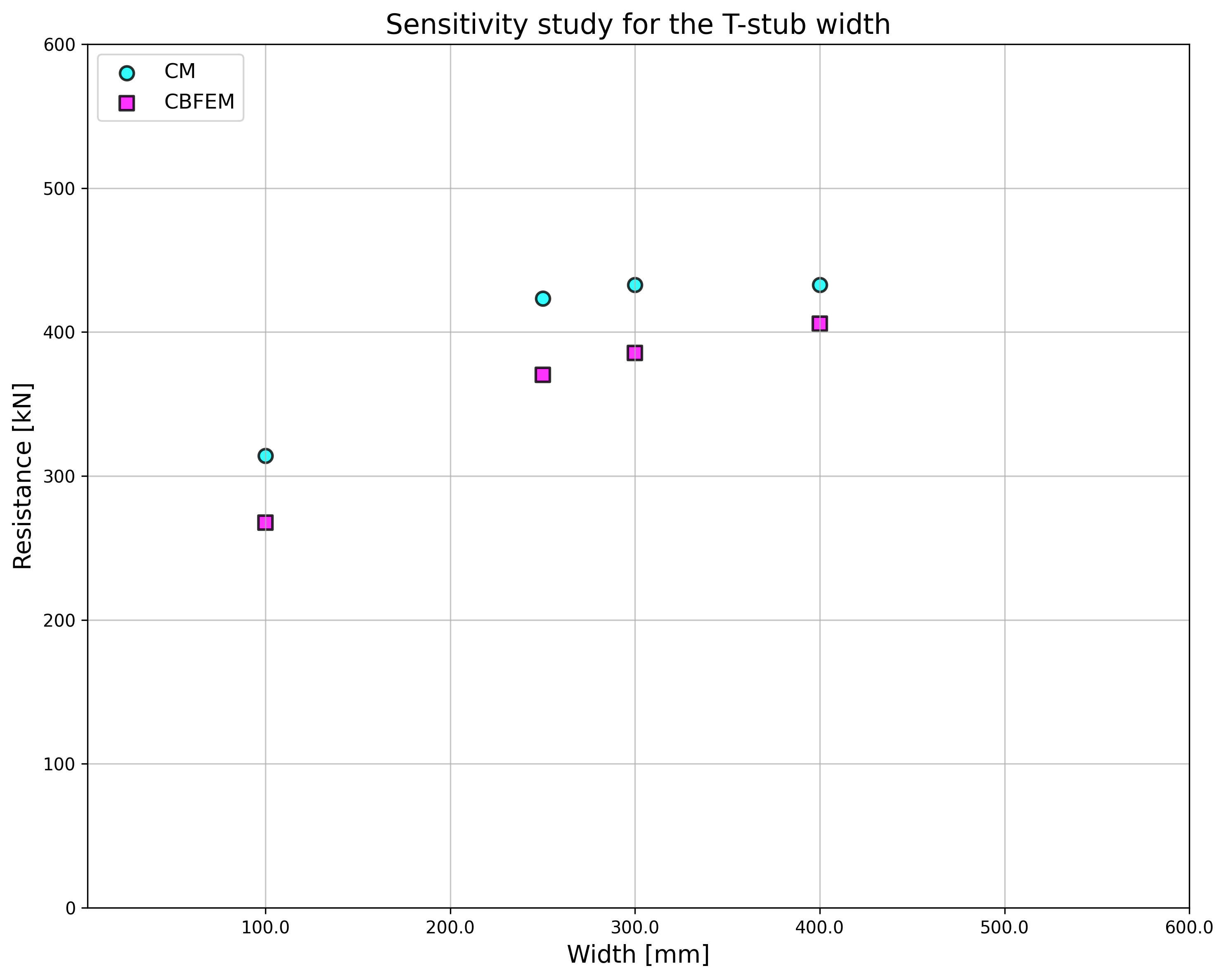
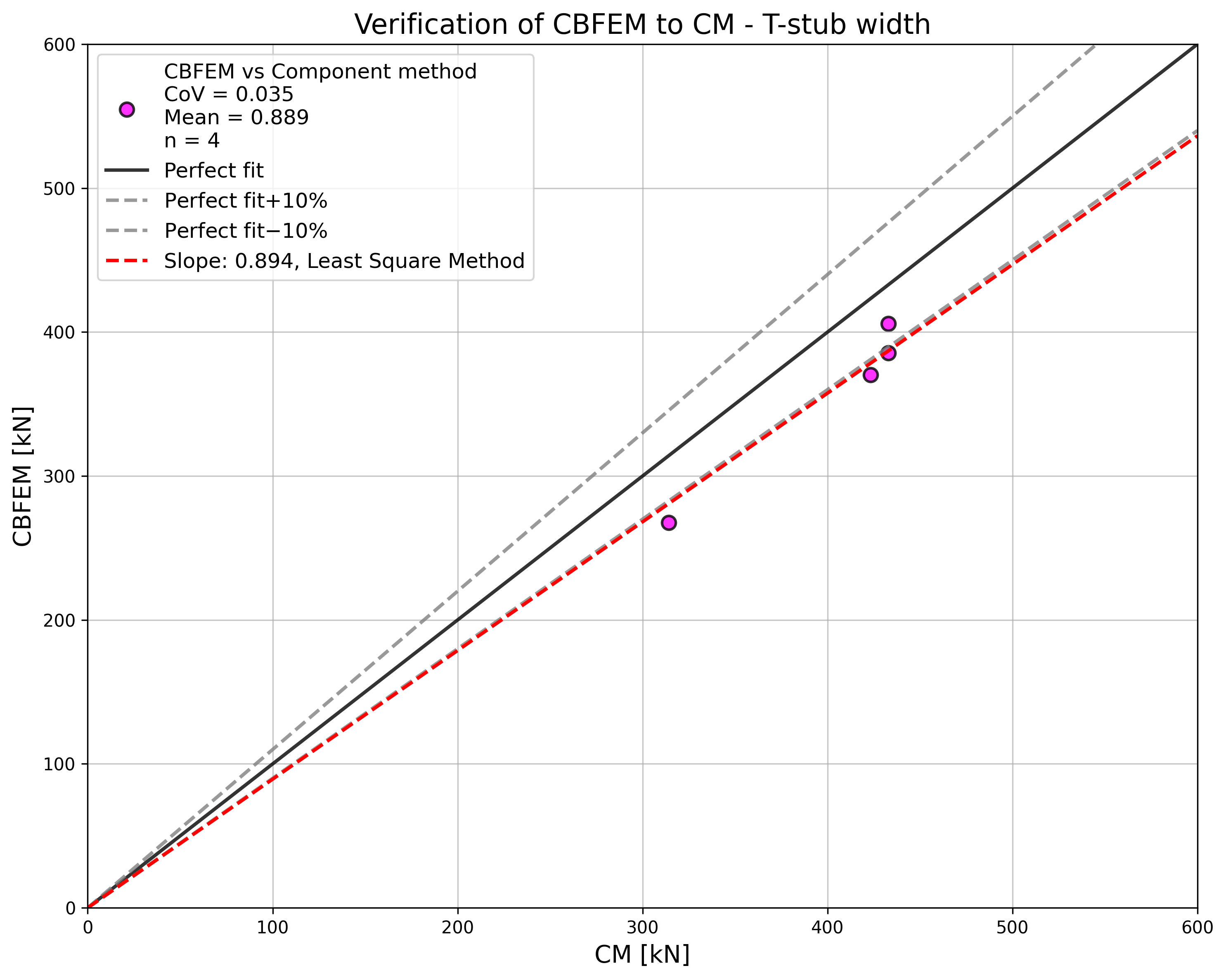
In the study of T-stub width, CBFEM shows higher resistance compared to CM with an increase in width. Results of RM were prepared, which again provide the highest resistance in all cases; see Fig. 5.1.9.
Fig. 5.1.9 Sensitivity study of T-stub width
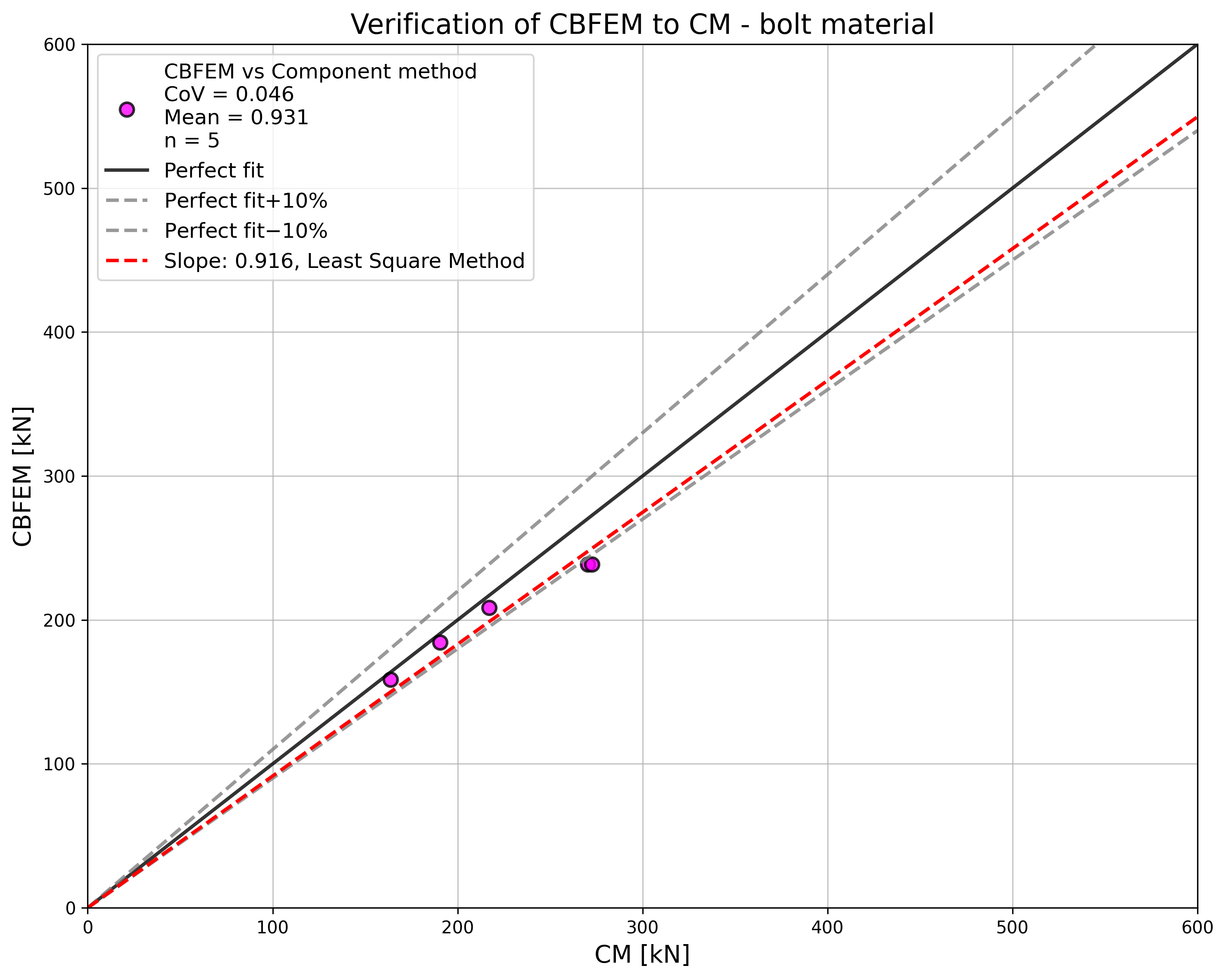
To show the prediction of the CBFEM model, the results of the studies were summarized in graph comparing resistances by CBFEM and CM; see Fig. 5.1.10. The results show that the difference between the two calculation methods is mostly up to 10 %. In cases with CBFEM/CM > 1,1, accuracy of CBFEM was verified by the results of RM, which gives the highest resistance in all selected cases.
Fig. 5.1.10 Summary of verification of CBFEM to CM
Benchmark example
Inputs
T-stub, see Fig. 5.1.11
- Steel S235
- Flange thickness tf = 20 mm
- Web thickness tw = 20 mm
- Flange width bf = 300 mm
- Length b = 100 mm
- Double fillet weld aw = 10 mm
Bolts
- 2 × M24 8.8
- Distance of the bolts w = 165 mm
Code setup – Model and mesh
- Number of elements on biggest member or flange 16
Outputs
- Design resistance in tension FT,Rd = 161,5 kN
- Collapse mode – full yielding of the flange with maximal strain 5 %
- Utilization of the bolts 86,4 %
- Utilization of the welds 45,7 %
Fig. 5.1.11 Benchmark example for the T-stub
References
EN 1993-1-5, Eurocode 3, Design of steel structures – Part 1-5: Plated Structural Elements, CEN, Brussels, 2005.
EN 1993-1-8, Eurocode 3, Design of steel structures – Part 1-8: Design of joints, CEN, Brussels, 2005.
Beg D., Zupančič E., Vayas I. On the rotation capacity of moment connections, Journal of Constructional Steel Research, 60 (3–5), 2004, 601–620.
Gödrich L., Wald F., Sokol Z. To Advanced modelling of end plate joints, Connection and Joints in Steel and Composite Structures, Rzeszow, 2013.
Gödrich L., Wald F., Kabeláč J., Kuříková M. Design finite element model of a bolted T-stub connection component, Journal of Constructional Steel Research. 2019, (157), 198-206.
Wu Z., Zhang S., Jiang S. Simulation of tensile bolts in finite element modelling of semi-rigid beam-to-column connections, International Journal of Steel Structures 12 (3), 2012, 339-350.