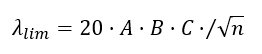Second-order effects in RCS application
Designing a compression member can be a complex task, requiring consideration of numerous factors and parameters. In particular, imperfections and second-order effects can have a significant impact on design internal forces, which must be taken into account to ensure a safe and efficient structure.
Two methods are implemented in the application:
- Nominal stiffness
- Nominal curvature
Both of them are according to EN 1992-1-1 articles 5.8.7 and 5.7.8. Member type has to be set as a Compression Member to access the functionality.
For more info about member types that can be set in the application, see the article Section and member types in the RCS application.
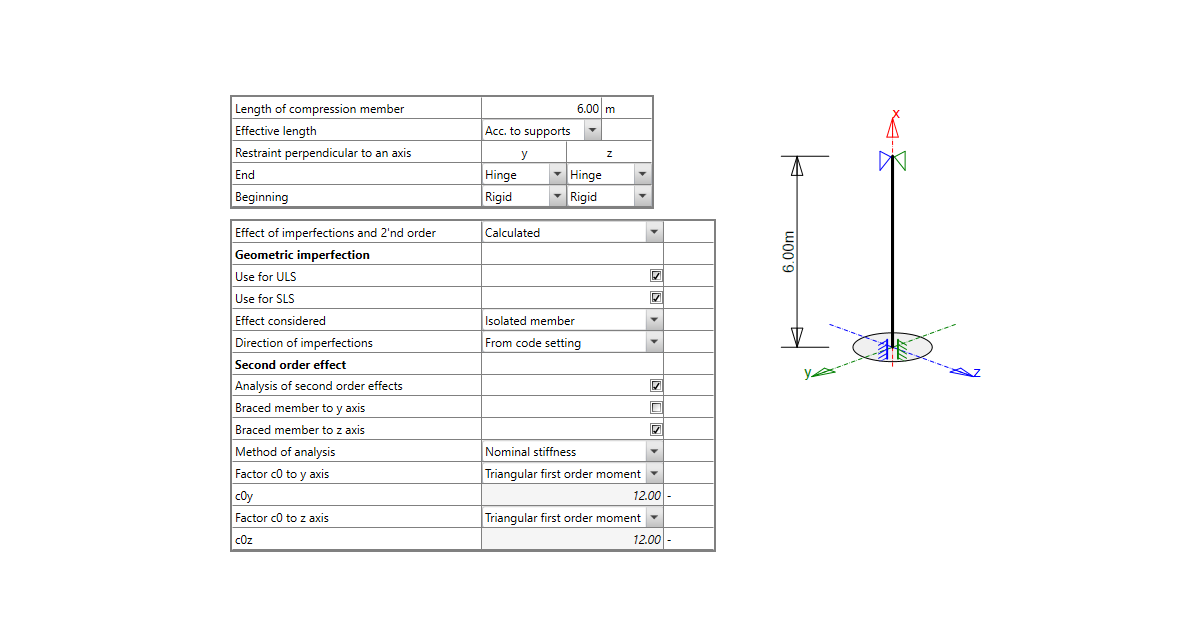
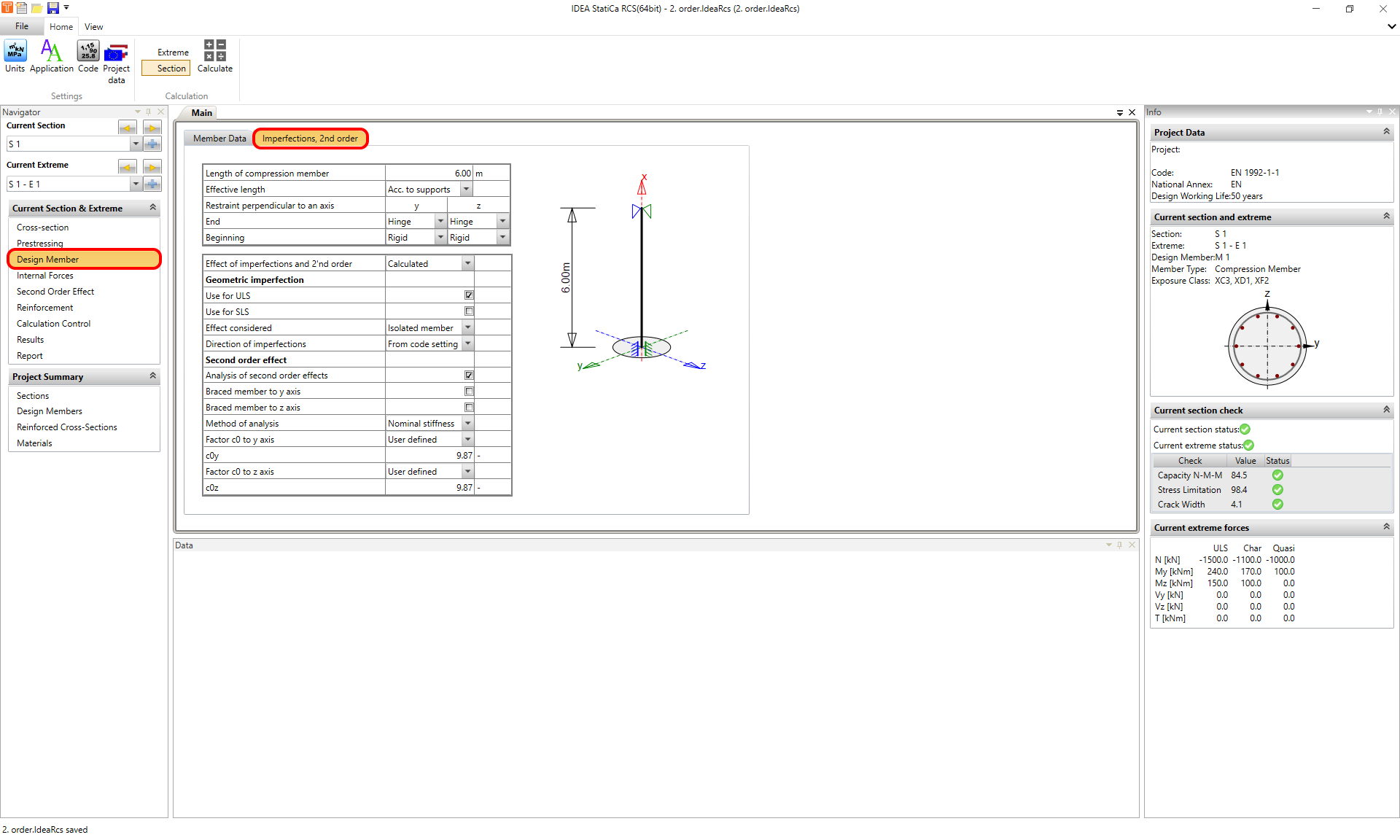
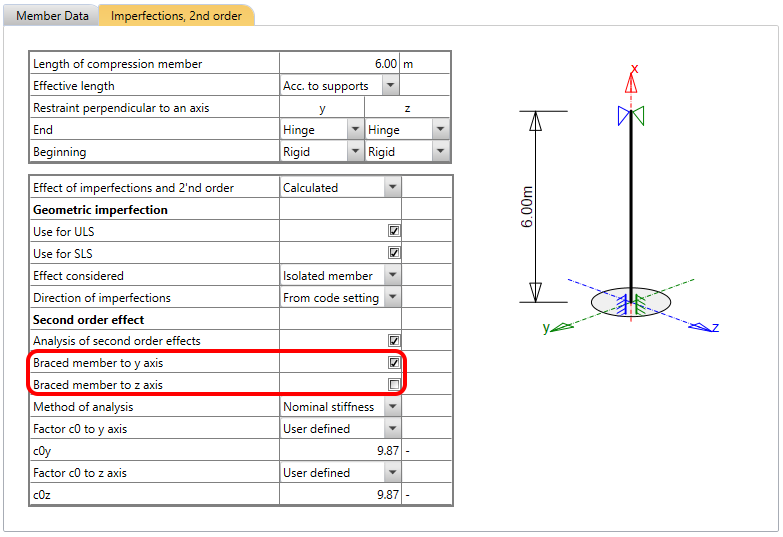
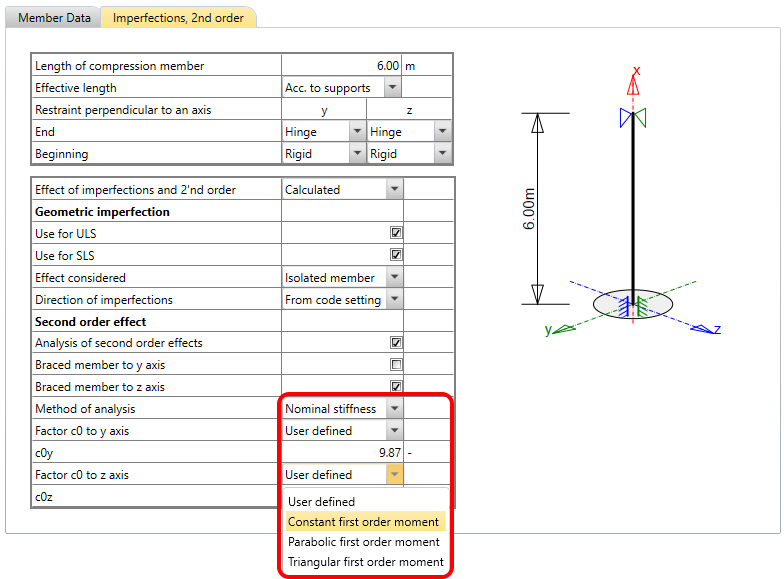
Once you have your cross-section created, loaded, and reinforced, go to the Navigator -> Design Member and select Imperfections, 2nd order. Here you can set the effective length and all parameters that are needed for the calculation of design internal forces.
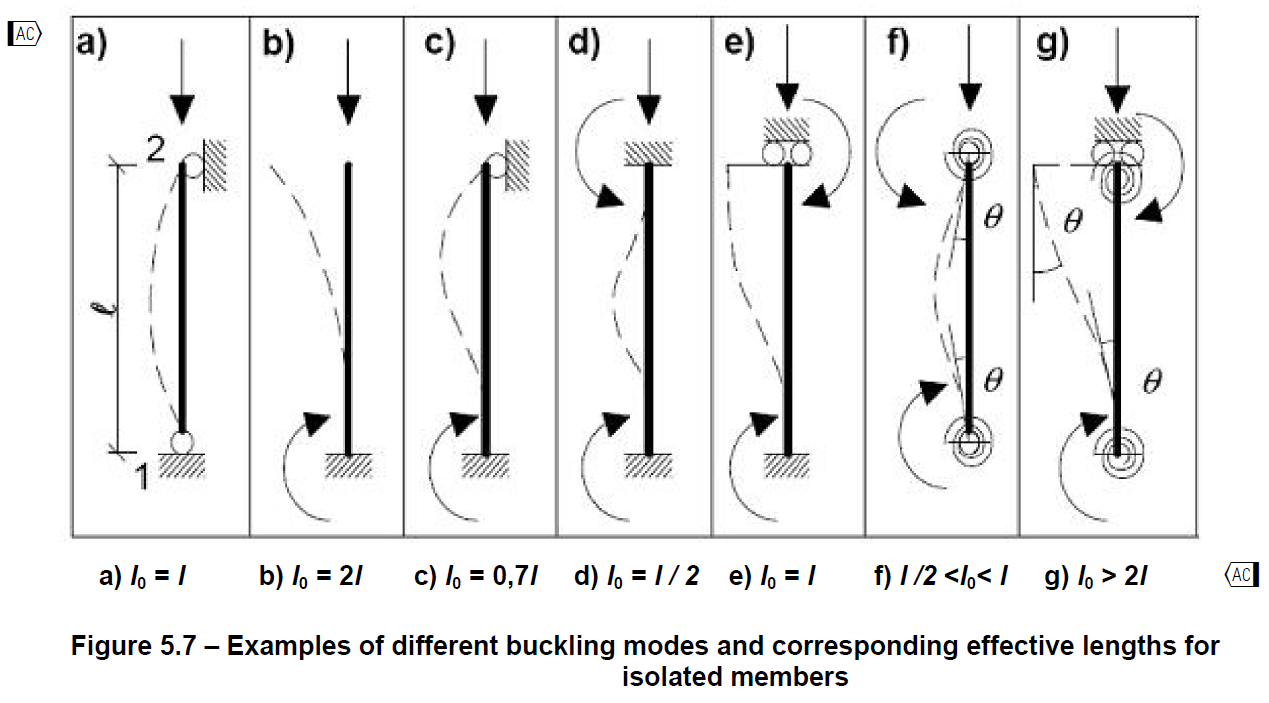
Effective length can be calculated automatically according to restraints perpendicular to the "y" axis or the "z" axis. This is done according to EN 1992-1-1 Figure 5.7, where the l0 is the Length of the compression member in the application.
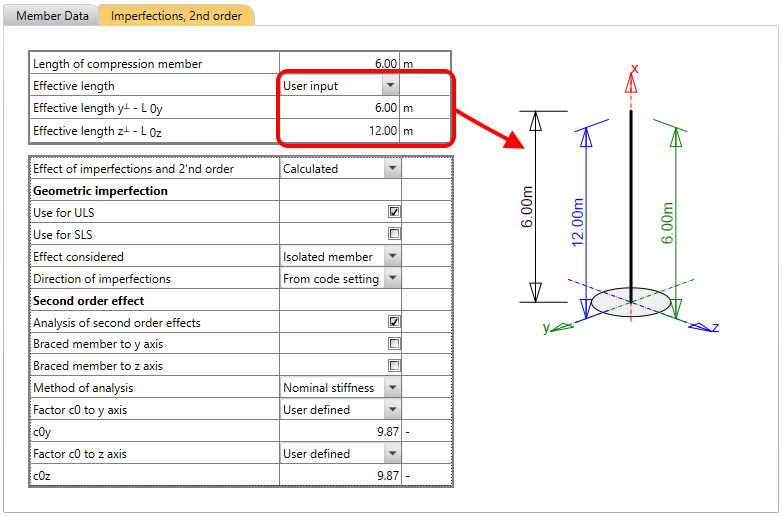
Or, if you know the effective length already, you can set it as User input.
If you select the Effect of imperfections and 2'nd order as Calculated, you will have to set the parameters for the geometric imperfection and second order effect in the table.
Let's go through the settings and learn about them.
Geometric imperfection
Geometric imperfection is calculated according to EN 1992-1-1 article 5.2.
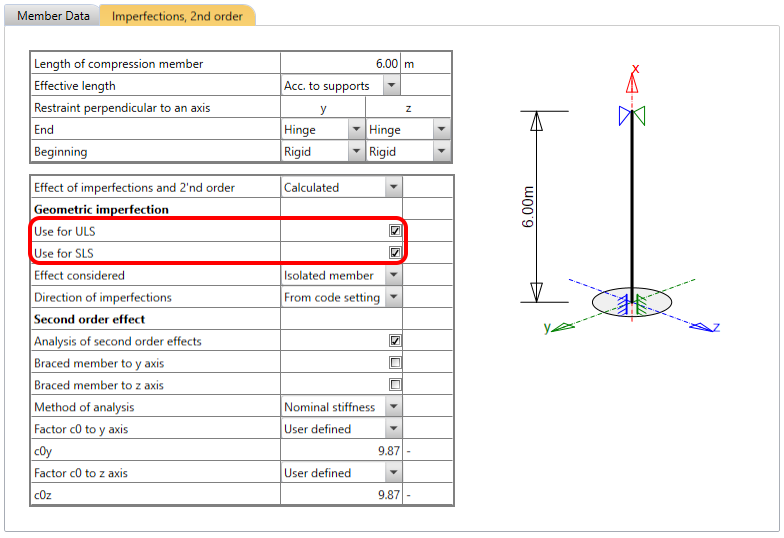
First, you have to decide if you want to apply imperfection only for ULS or SLS or for both ULS and SLS.
Note that for SLS only the imperfection ei is applied. There is no need to apply e2 eccentricity caused by 2nd order effect for SLS according to the code.
After selecting the corresponding combinations' set, you have to set the cell called Effect considered. There are two options for this functionality:
- Isolated member
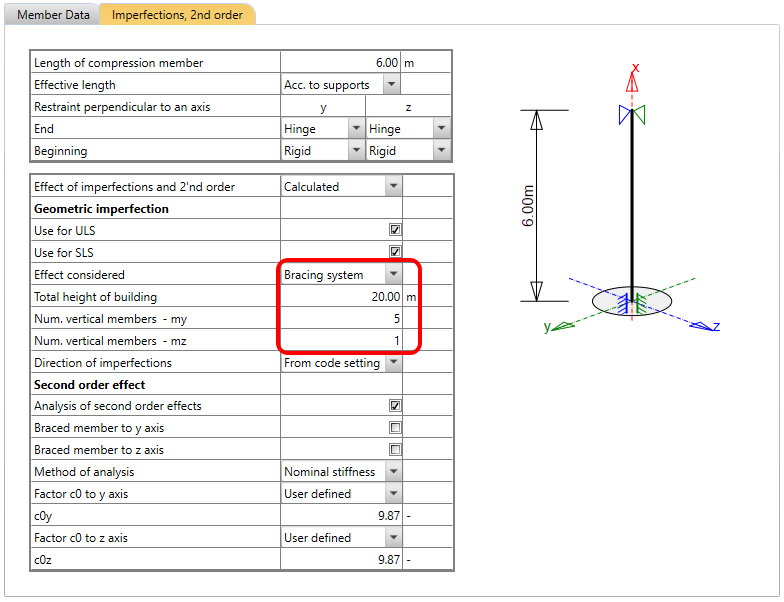
- Bracing system
You can find the explanation in EN 1992-1-1 5.2(6).
According to the code's paragraph, the parameters for the Isolated member are as follows:
l (length) = actual length of the member
m (number of vertical members) = 1
The parameters for the Bracing system are:
l = height of building
m = number of vertical members contributing to the horizontal force on the bracing system in both directions
Another important setting is the Direction of imperfections. There are three options:
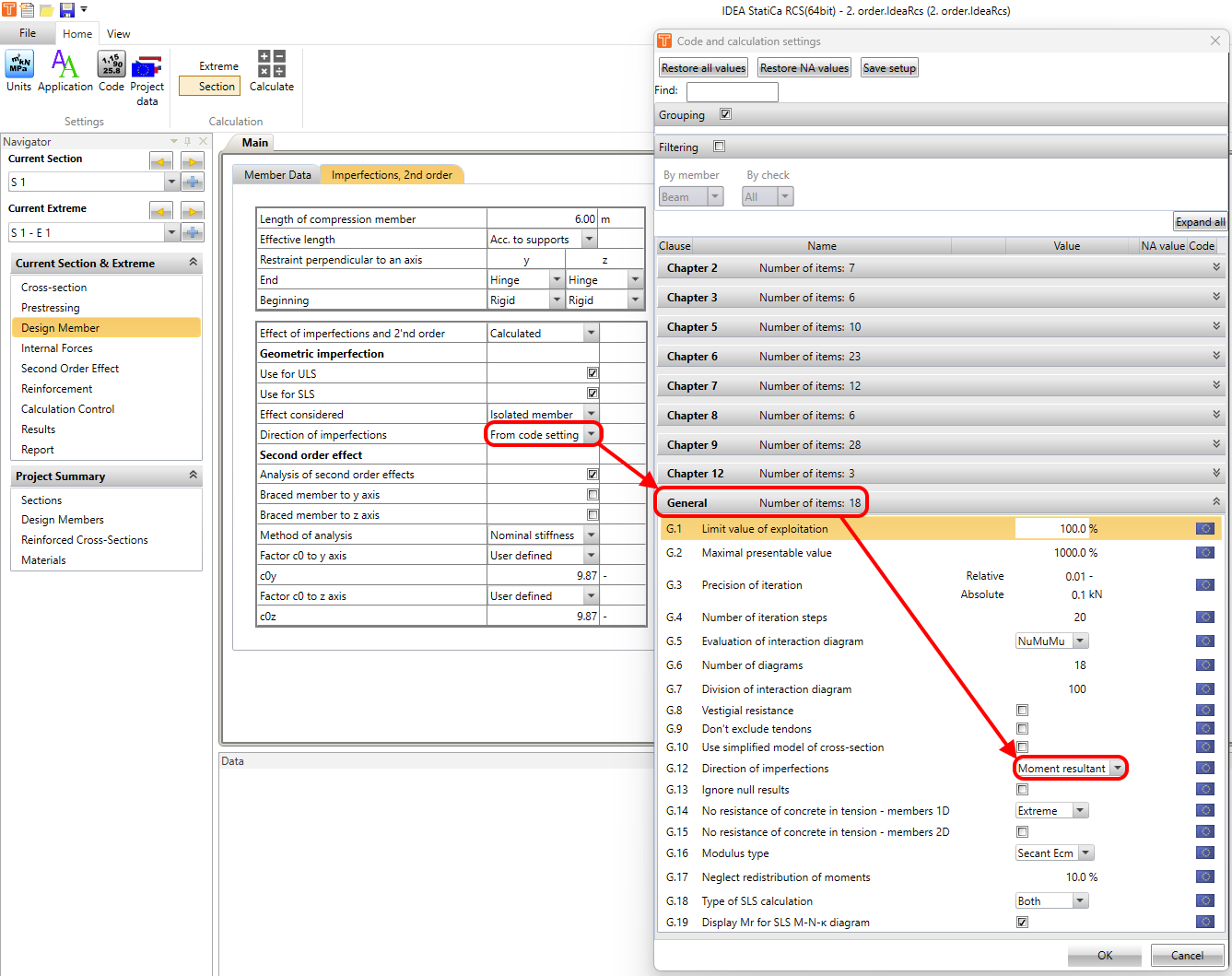
1. From code setting
It means that the option set in code settings will be used for the calculation.
2. Moment resultant
Mi,Ed,y/z = NEd * ei,y/z
where:
NEd is design normal force
ei,y/z is geometric imperfection
Mi,Ed,y/z is a bending moment caused by imperfection
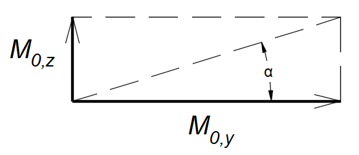
Mi,Ed,y = M0,y + Mi,Ed,y/z * cos (α)
where:
M0,y is first order bending moment about the "z" axis
α is an angle shown in the figure below
Mi,Ed,y is the first order bending moment about the "z" axis, including the effect of imperfections
- Read the following article to learn How to calculate resultant first order eccentricity on the compression member
3. Bigger slenderness
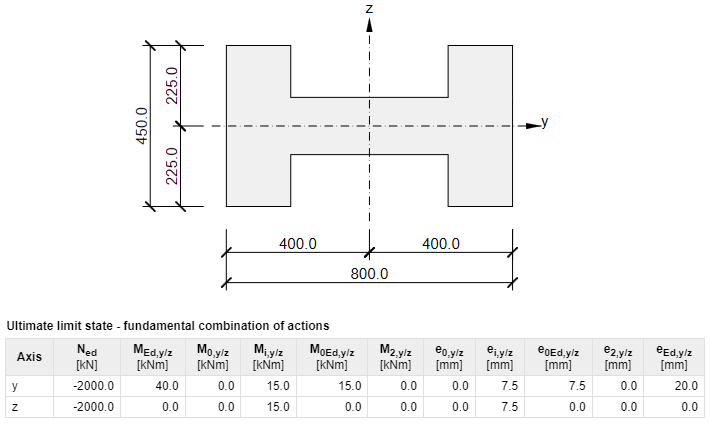
This option applies the whole geometric imperfection to the direction of bigger slenderness. For example, only Mi,Ed,y will be considered for the section shown in the image below.
Second order effect
In the bottom part of the table, you can set the analysis of second order effects. Before you choose the calculation method, it is necessary to know if your member is braced or not and in which direction.
This setting influences the calculation of the Slenderness criterion for isolated members according to EN 1992-1-1 article 5.8.3.1 (1).
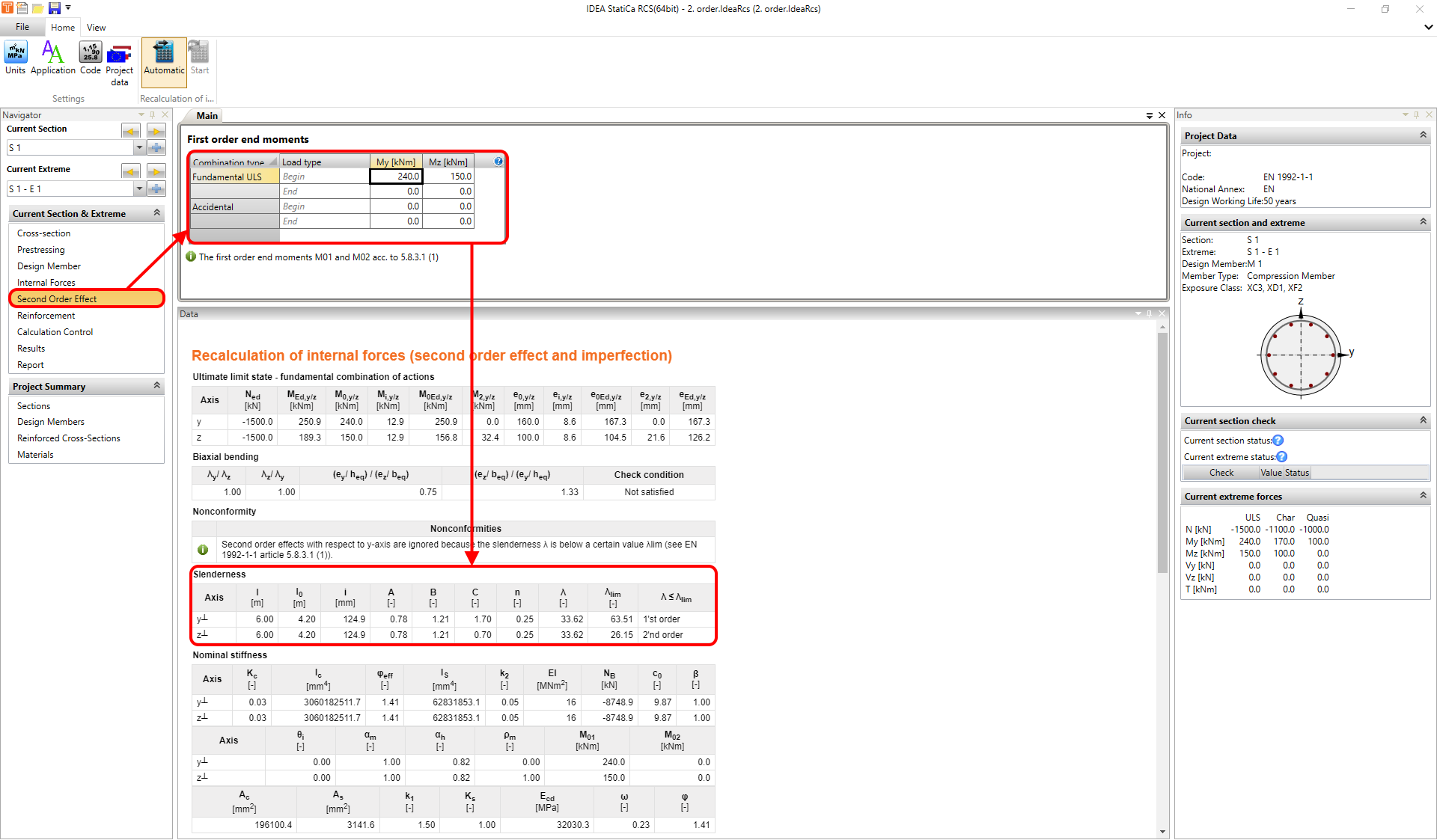
For the calculation of the moment ratio rm factor, you need to set the first order end moments M01 and M02. This can be done in Navigator -> Second Order Effect.
Two methods of analysis are implemented in the software:
- Nominal stiffness
- Nominal curvature
Nominal stiffness
For nominal stiffness, you must define the c0 factor. The description can be found in EN 1992-1-1 article 5.8.7.2 (2)(3).
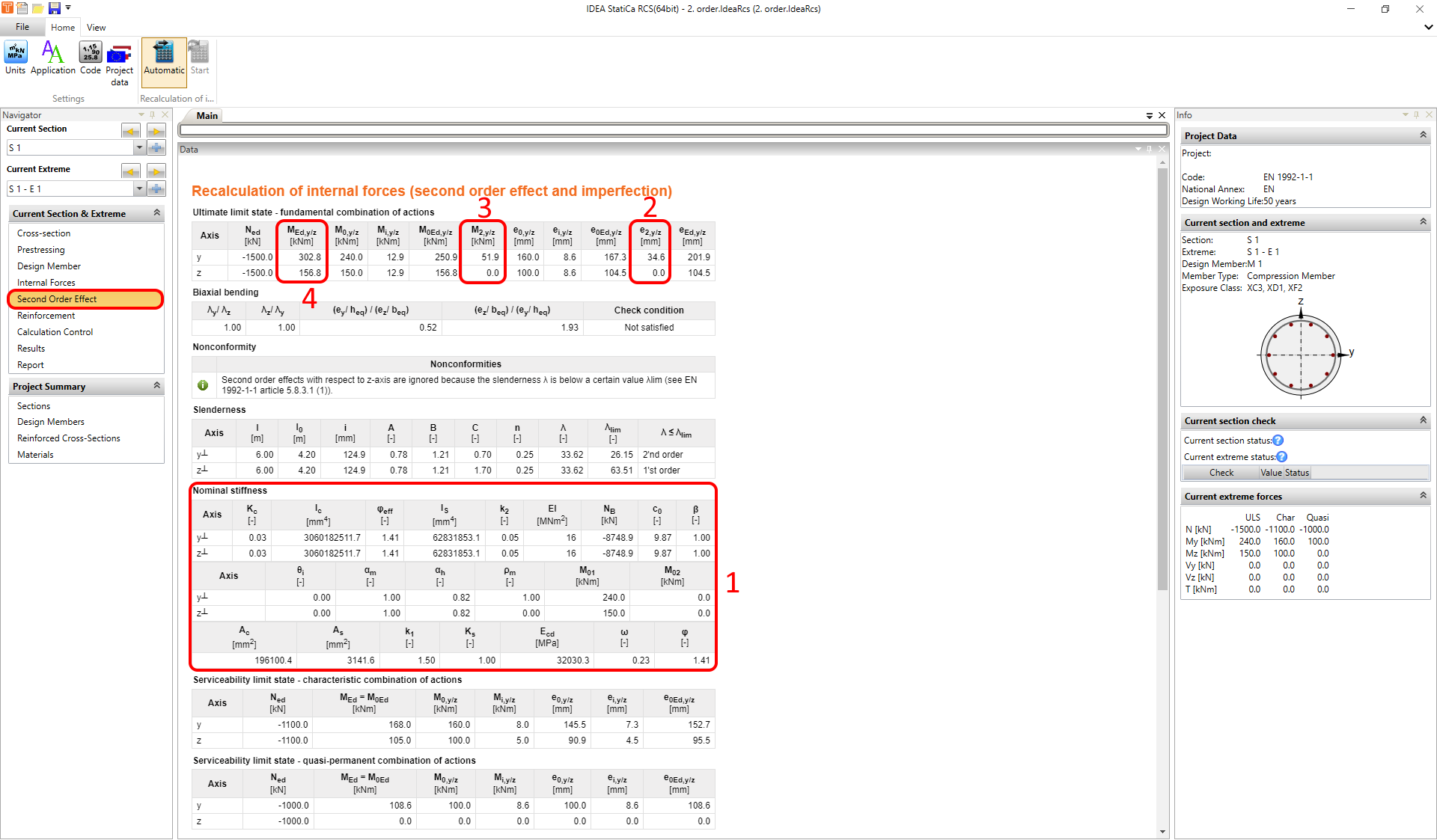
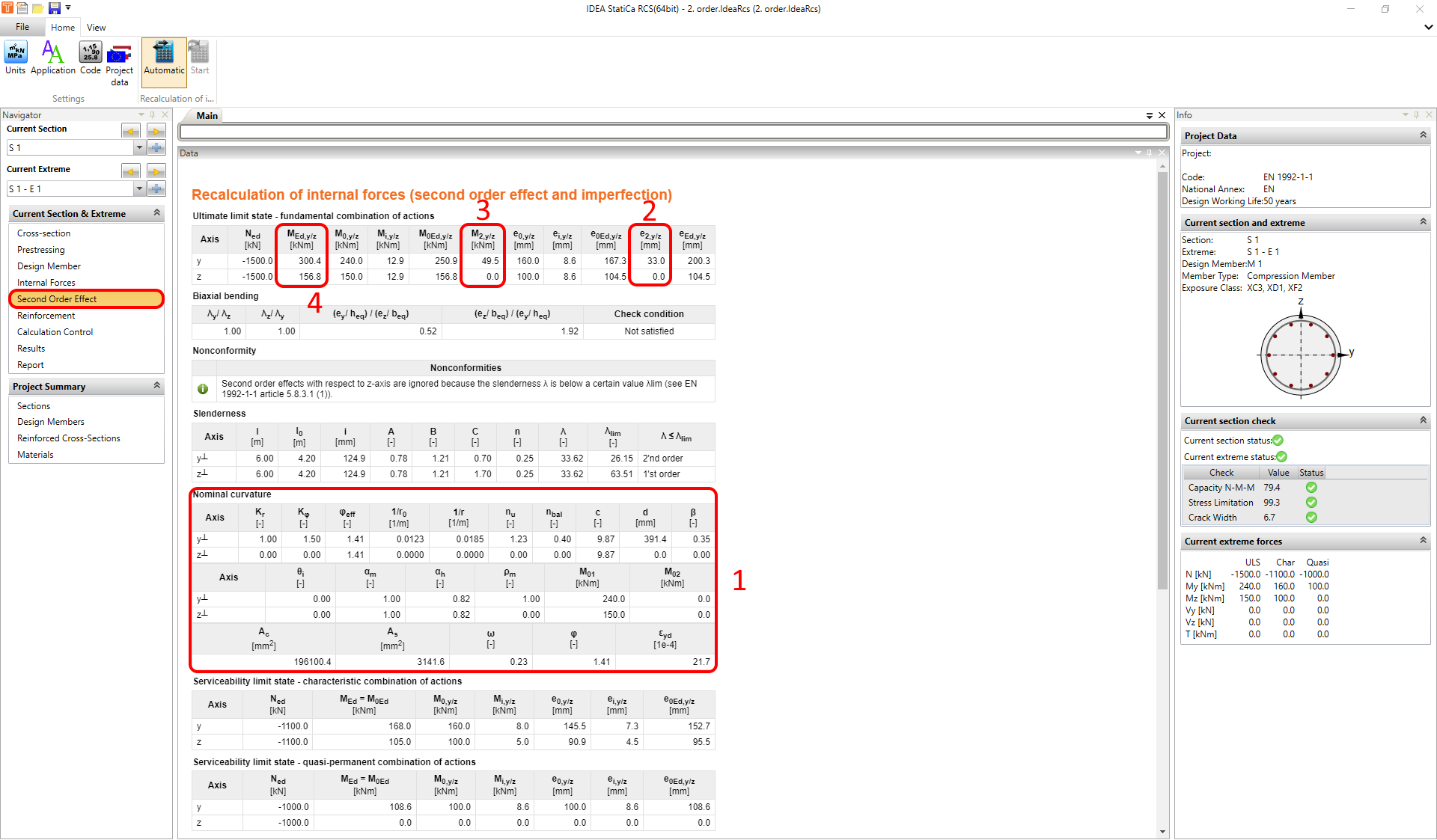
All intermediate results can be explored in Navigator -> Second Order Effect. The final result is the design moment about the "y" and "z" axis, respectively.
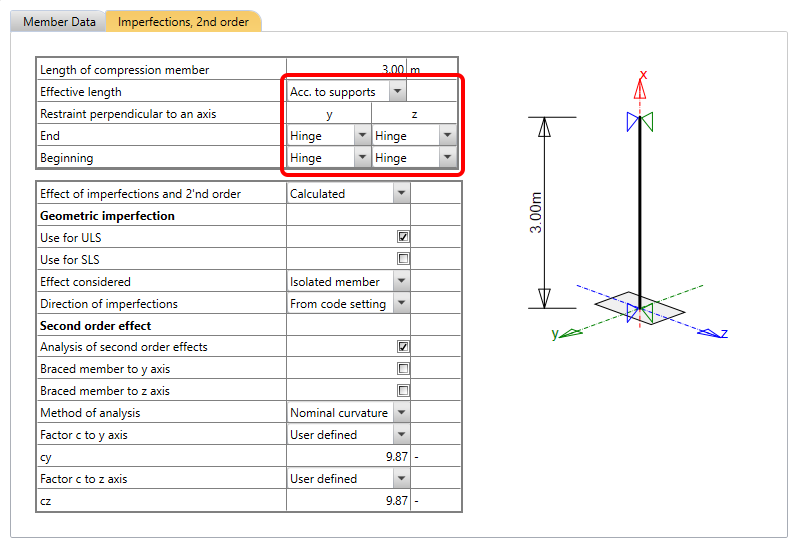
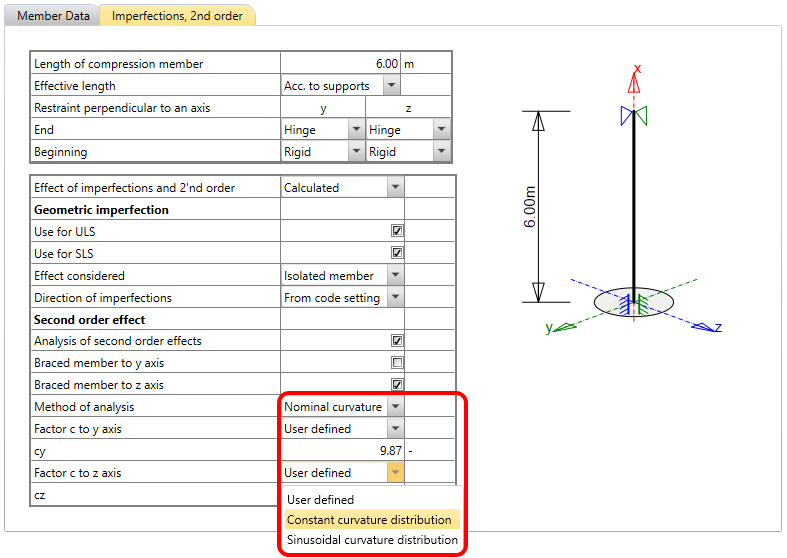
Nominal curvature
For nominal curvature, you have to set the c factor. The description can be found in EN 1992-1-1 article 5.8.8.2 (3)(4).
As for the previous method, all intermediate results can be explored in Navigator -> Second Order Effect. The final result is the design moment about the "y" and "z" axis, respectively.
Be aware that for SLS checks, the assumption MEd = M0Ed is valid. It means that no second-order effect is included for SLS. I.e., only the imperfections are included.
Biaxial bending
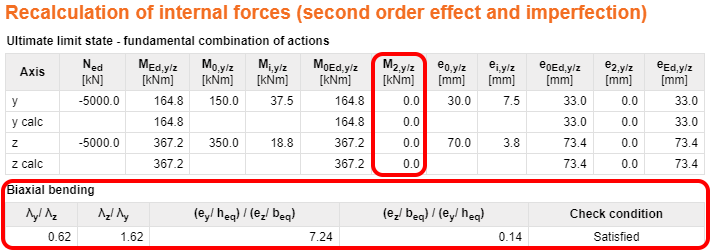
No further check is necessary if the slenderness ratios satisfy the highlighted two conditions in the image below.
I.e., the application will not consider the M2,y/z moment if the check conditions are satisfied.