Plate model and mesh convergence
Increase in number of elements provides more precise results but at the cost of higher computational demand.
Plate model
Shell elements are recommended for modeling of plates in the FEA of structural connection. 4-node quadrangle shell elements with nodes at its corners are applied. Six degrees of freedom are considered in each node: 3 translations (ux, uy, uz) and 3 rotations (φx, φy, φz). Deformations of the element are divided into the membrane and the flexural components.
The formulation of the membrane behavior is based on the work by Ibrahimbegovic (1990). Rotations perpendicular to the plane of the element are considered. Complete 3D formulation of the element is provided. The out-of-plane shear deformations are considered in the formulation of the flexural behavior of an element based on Mindlin hypothesis. Our inhouse stabilised variant of Mindlin quad plate element with constat shear deforamtion along edge are applied. The elements are inspired by MITC4 elements; see Dvorkin (1984). The shell is divided into five integration layers through thickness of the plate at each integration point and plastic behavior is analyzed in each point. It is called Gauss–Lobatto integration. The nonlinear elastic-plastic stage of material is analyzed in each layer based on the known strains. Only the maximum stresses and strains of all layers are shown.
Mesh convergence
There are some criteria for the mesh generation in the connection model. The connection check should be independent of the element size. Mesh generation on a separate plate is problem-free. Attention should be paid to complex geometries such as stiffened panels, T-stubs, and base plates. The sensitivity analysis considering mesh discretization should be performed for complicated geometries.
All plates of a beam cross-section have a common division into elements. The size of generated finite elements is limited. The minimal element size is set to 10 mm and the maximal element size to 50 mm (can be set in Code setup). Meshes on flanges and webs are independent of each other. The default number of finite elements is set to 8 elements per cross-section height as shown in the following figure. The user can modify the default values in Code setup.
The mesh on a beam with constraints between the web and the flange plate
The mesh of the end plates is separate and independent of other connection parts. Default finite element size is set to 16 elements per cross-section height as shown in the figure.
The mesh on an end plate with 7 elements along its width
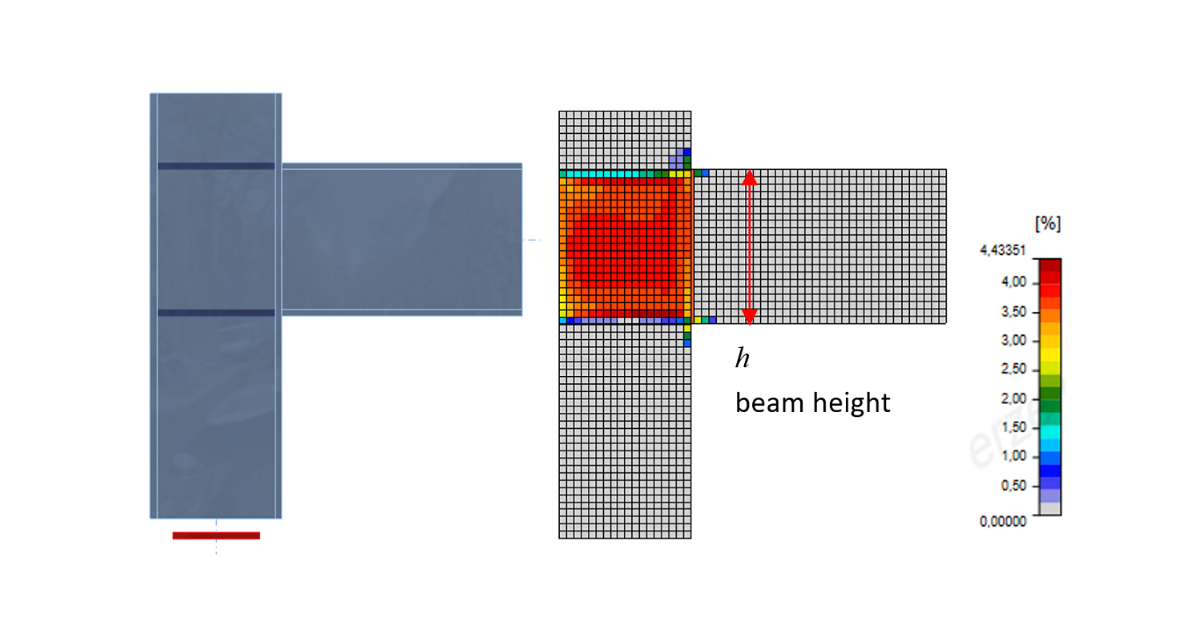
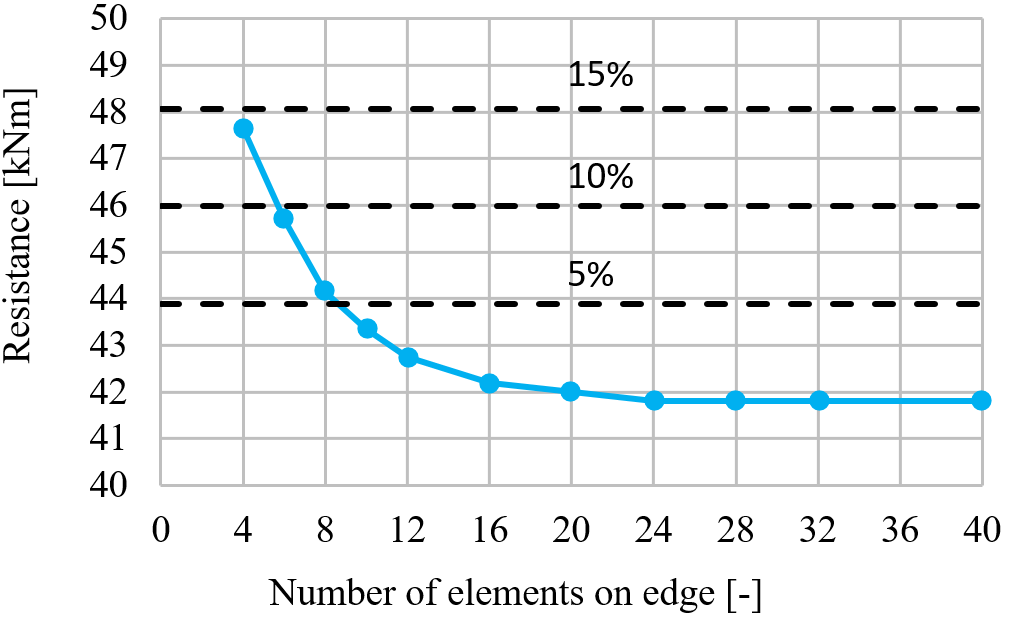
The following example of a beam to column joint shows the influence of mesh size on the moment resistance. An open section beam IPE 220 is connected to an open section column HEA 200 and loaded by a bending moment as shown in the following figure. The critical component is the column panel in shear. The number of the finite elements along the cross-section height varies from 4 to 40 and the results are compared. Dashed lines are representing the 5%, 10%, and 15% difference. It is recommended to subdivide the cross-section height into 8 elements.
A beam to column joint model and plastic strains at ultimate limit state
The influence of the number of elements on the moment resistance
The mesh sensitivity study of a slender compressed stiffener of column web panel is presented. The number of elements along the width of the stiffener varies from 4 to 20. The first buckling mode and the influence of a number of elements on the buckling resistance and critical load are shown in the following figure. The difference of 5% and 10% is displayed. It is recommended to use 8 elements along the stiffener width.
The first buckling mode and the influence of number of elements along the stiffener on the moment resistance
The mesh sensitivity study of a T-stub in tension is presented. Half of the flange width is subdivided into 8 to 40 elements, and the minimal element size is set to 1 mm. The influence of the number of elements on the T-stub resistance is shown in the following figure. The dashed lines are representing the 5%, 10%, and 15% difference. It is recommended to use 16 elements on the half of the flange width.
The influence of the number of elements on the T-stub resistance