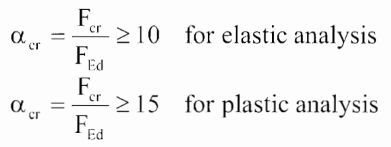Global buckling vs. local buckling. What does it mean?
The design code says that first-order analysis may be used for the structure if the increase of the relevant internal forces or moments or any other change of structural behavior caused by deformations can be neglected.
To evaluate whether this increase can or can't be neglected the critical buckling factor αcr can be used. We can neglect the global buckling for members, (including the connection) in cases where the buckling factor is higher than 15 (in case of plastic design) or higher than 10 (in case the stress on plates is on elastic branch).
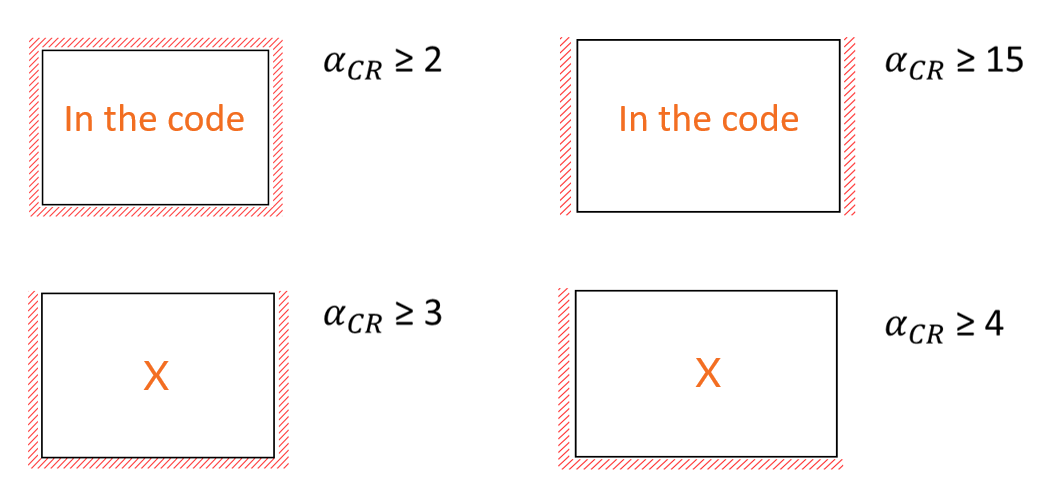
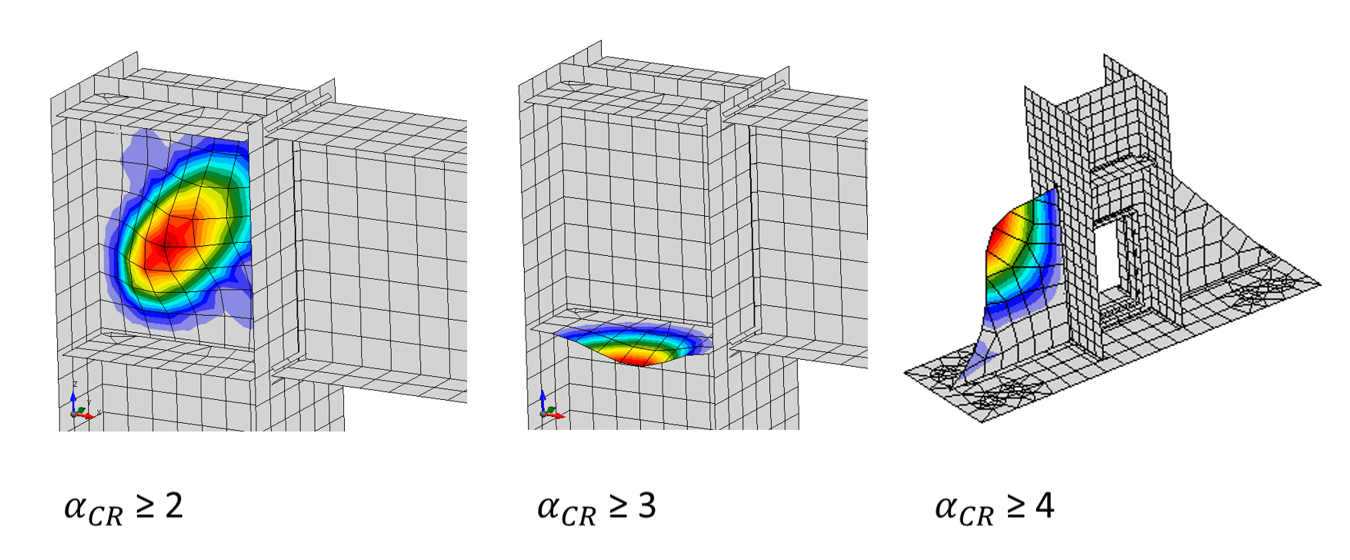
Local buckling applies to individual plates (stiffeners, column web), and the corresponding limiting buckling factors are set according to design codes and research experiments. The effects of local buckling are considered to be neglectable when the buckling factor is:
- ≥ 2 - in case of a 4-sided supported plate
- ≥ 3 - in case of a 3-sided supported plate
- ≥ 4 - in case of a 2-sided (neighboring) supported plate
- ≥ 15 - in case of a 2-sided (opposite) supported plate
In the video, you can see different types of buckling and how to deal with them, considering the buckling factors and buckling shapes.
For a more comprehensive explanation of what types of buckling we can expect in the analyzed member, go through our article about Linear buckling analysis (LBA).
How to evaluate the buckling results in specific cases?
First of all, we have to determine the minimum force amplifier to reach the elastic critical buckling, αcr using buckling analysis. IDEA StatiCa provides the buckling factors in result tables and the buckling shapes for each factor can be provided in a 3D view.
The limit value for global analysis can be found in EN 1993-1-1:2005 Cl. 5.2.1.
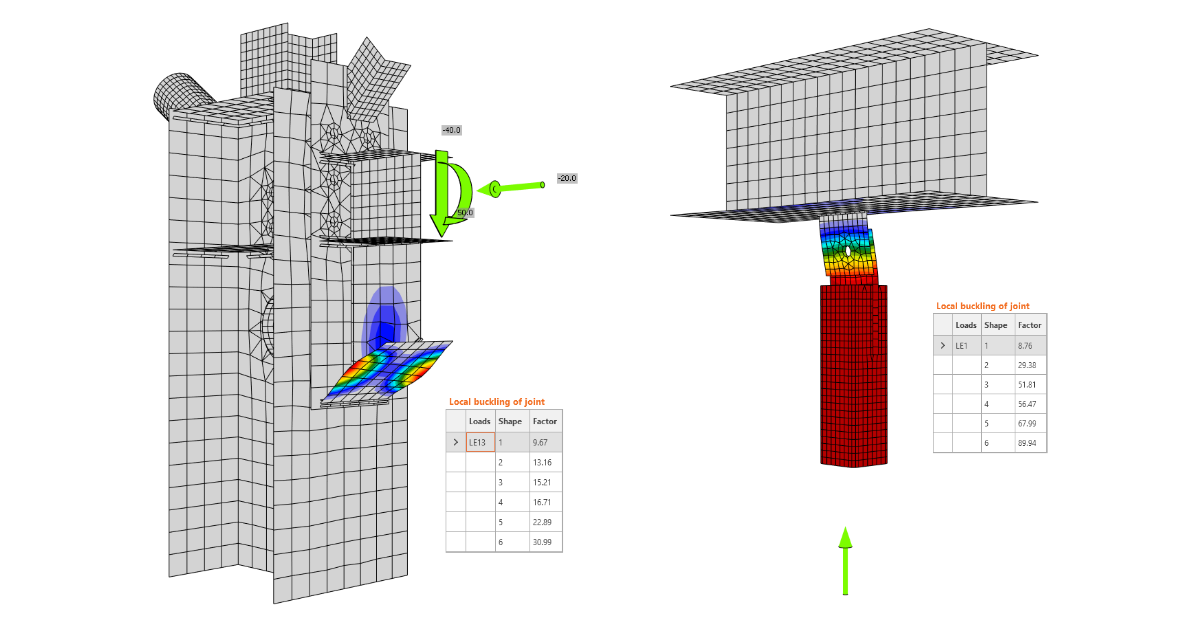
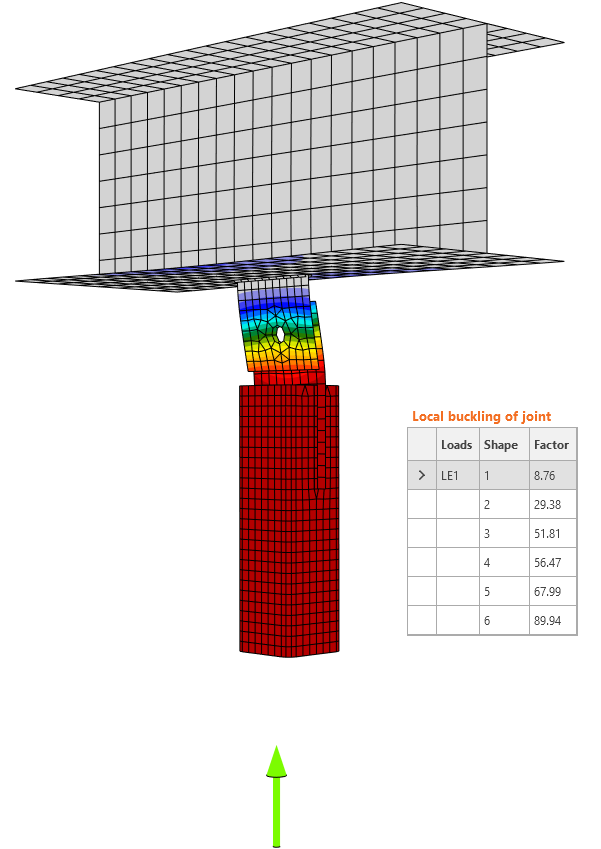
Example 1
In the first example, the pressure force is applied to the beam connected by a connecting plate.
The results from the geometrically linear calculation are provided and the first factor is 8,76. According to EN 1993-1-1:2005 Cl. 5.2.1, the limit value is 15 because this joint is critical for the stability of the beam itself and the conclusion is the connection did not pass the buckling analysis. Not to mention that this one-sided connecting plate is dangerous in this bracing in the pressure configuration.
Read further here on how to calculate buckling resistance of a gusset plate.
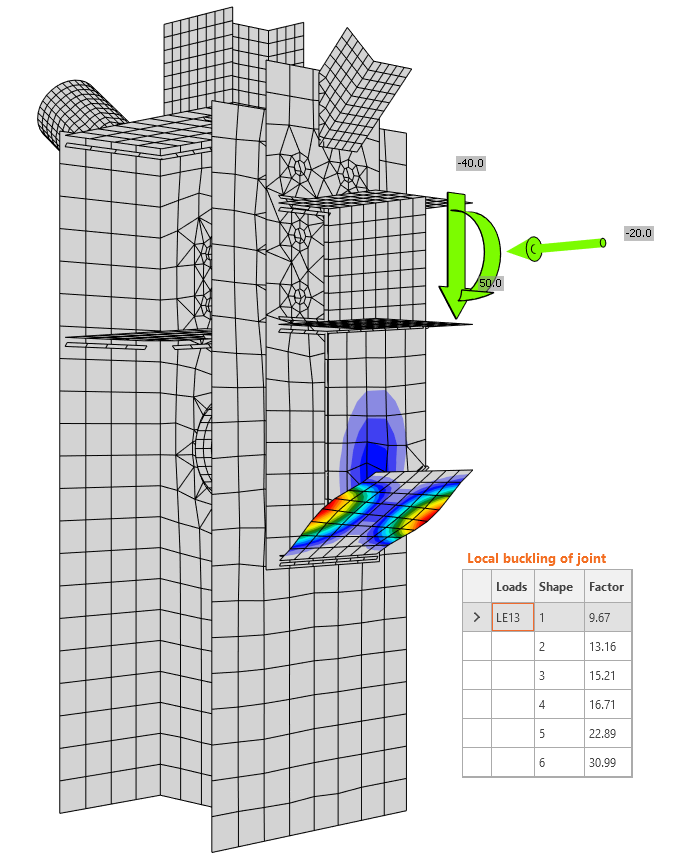
Example 2
On the other hand, in the case of most plates in connections, local buckling can occur and the maximum value of the critical buckling factor, αcr, that requires thorough analysis is usually smaller. It has been verified that for stiffeners and column panel in shear, it is not necessary to take into account buckling if the critical buckling factor is higher than 3.
We have to determine the right limit value for each component and decide. This example shows that the first buckling mode is that of a stiffener with factor αcr = 8,76 >> 3. In this example, this first buckling mode is not dangerous.
While performing the buckling analysis and treating the results, engineering judgment needs to take place. The question is when to use global or local limits of the critical buckling factor and for the right answer, the knowledge of the topology and structural system of the designed structure is crucial. While IDEA StatiCa has the capacity to deliver buckling shapes and critical factor of any part of the joint, it does not provide the buckling code-check as per code.
When the results of buckling shapes give us negative values, it doesn't mean the calculation was unsuccessful or the result is incorrect. What exactly happens in these cases is explained in this knowledge base article.
One practical example of the member buckling analysis evaluation was presented in this webinar video:
Theoretical Background
For a deeper understanding of the buckling topic and IDEA StatiCa solution, read the essential information about buckling analysis in our Theoretical Background articles.
IDEA StatiCa Connection - Structural design of steel connections
IDEA StatiCa Member - Member stability
Tutorials
We have created step-by-step tutorials to set up the model and run the analysis. Find the links to them below:
Structural design of a steel cross-beam affected by lateral torsional buckling (EN)
Structural design and code-check of a steel frame (EN)