The best approach to determine the buckling resistance of a subsystem consisting of joint-member-joint is to use GMNIA (geometrically and materially nonlinear analysis with imperfections) in IDEA StatiCa Member application.
IDEA StatiCa Connection lacks the context of surrounding structure. Furthermore, geometrical nonlinearity is used only for joints of hollow sections and imperfections cannot be set. Linear buckling analysis provides a factor – a multiplier of set loads to reach bifurcation point of a perfect, elastic structure. Real structure will usually buckle under smaller load, and it is unclear what factor limit should be used for linear buckling analysis of gusset plates, i.e. a factor above which buckling is not a concern anymore.
Eurocode EN 1993-1-1 provides general recommendation:
\[\alpha_{cr} \le 15 \textrm{ for plastic analysis}\]
AISC 360-22 in Chapter J4.4 provides similar limit:
\[ L_c/r \le 25 \]
Which may be translated to a limit of \(\alpha_{cr}\) that depends on yield strength and the safest limit is 12.7 for A36 steel grade.
Such limits are very high. Factors below these limits should trigger a warning and a buckling limit state should be checked. However, \(\alpha_{cr}\) can hardly be translated into buckling resistance.
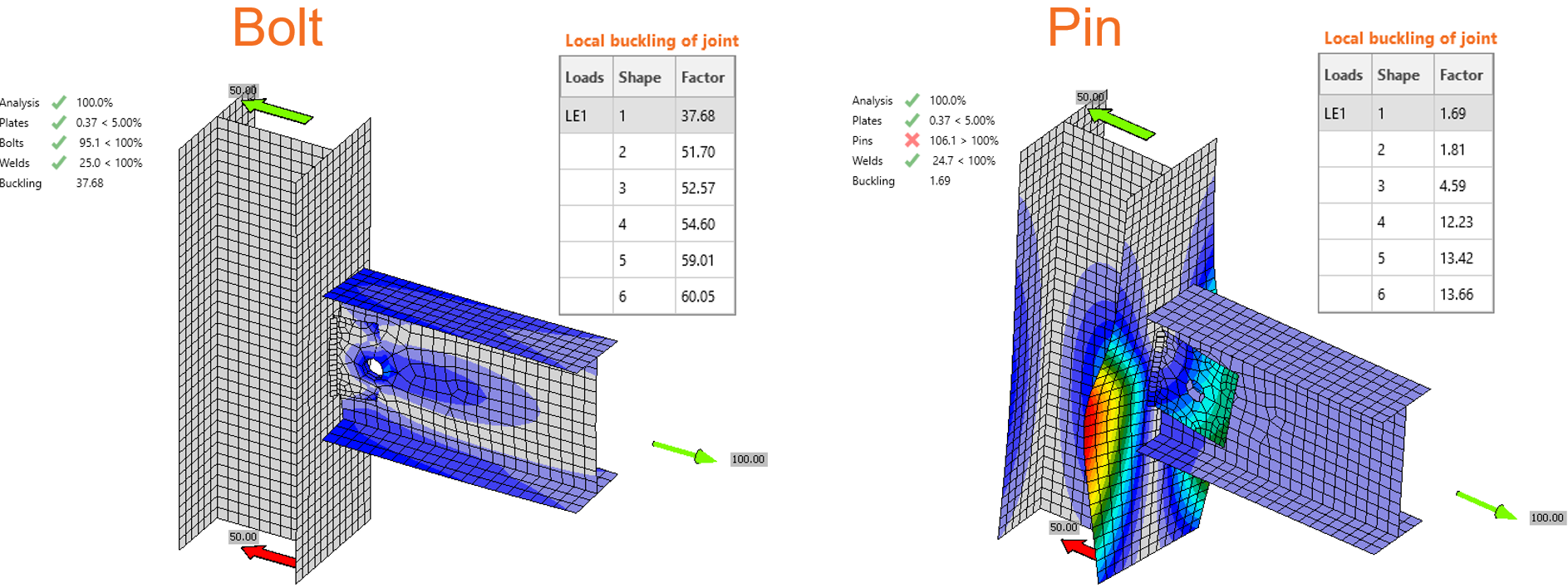
Also note that the bolted gusset plate connections provide reasonable buckling factors while connections with pins provide extremely low buckling factors. This is due to the analysis model of pin that consists of many special elements (rigid body elements, beam elements, gap elements...) and provides good results in terms of resistances of pin in shear, bending and bearing. Therefore a simple procedure is described below.
Buckling resistance check
This simplified buckling resistance check should be performed when buckling factor falls below the limit \(\alpha_{cr}\) mentioned above.
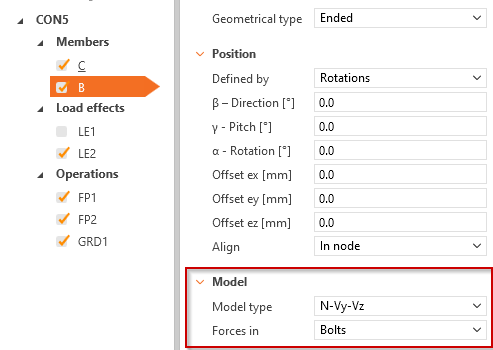
- Model type of member connected by gusset plate should be set to N-Vy-Vz.
- Forces in should be set to Bolts.
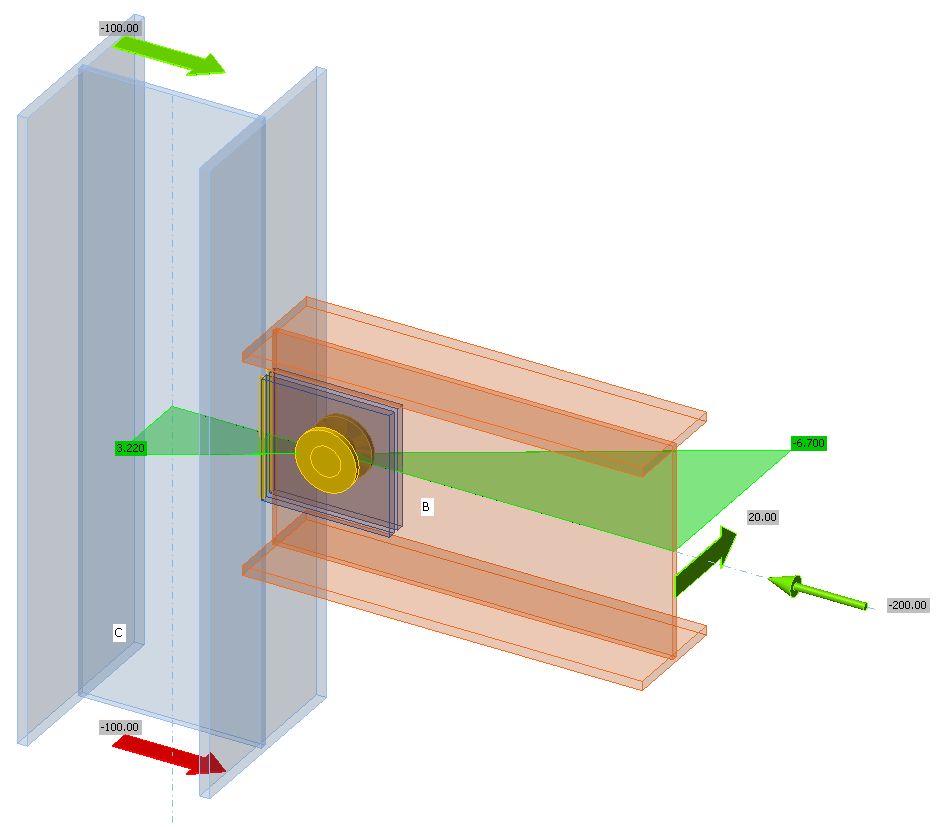
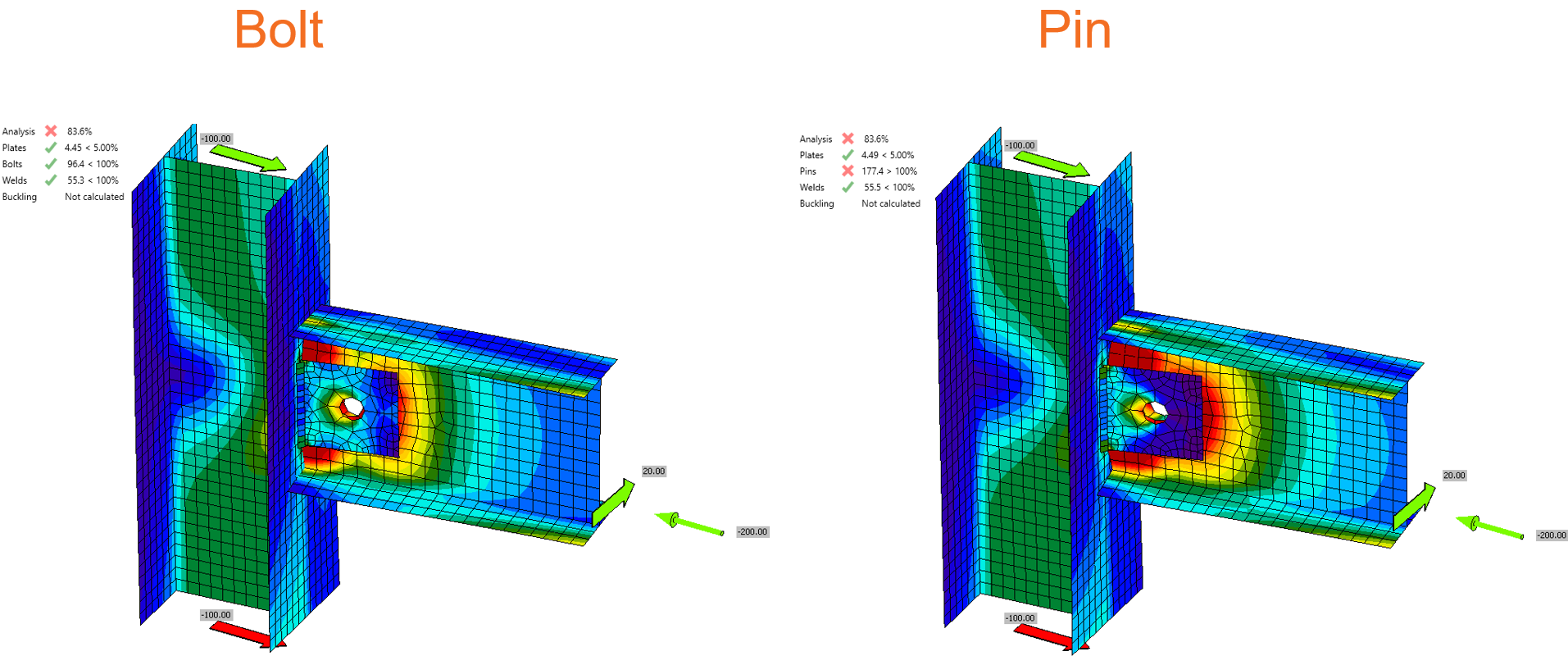
- Add a fictive shear force acting in the center of bolts or pin that bends the gusset plate with the magnitude of 1/10 of compressive force: \(V_z=N/10\).
- Calculate materially nonlinear analysis.
The fictive force takes into account any eccentricities caused by imperfections and geometrical nonlinearity. Validation to experiments is in the linked article.