Check of steel connection components (AS)
Bolts, preloaded bolts, and welds are checked according to AS 4100–2020, Chapter 9. The concrete bearing surface according to AS3600:2018 – Chapter 12.6. The check of anchors is provided according to AS 5216:2018. The design of shear lug and transfer of shear at the column base by friction is according to a publication: Gianluca Ranzi, Peter Kneen: Design of Pinned Column Base Plates, Journal of the Australian Steel Institute, vol. 36, no. 2, September 2002.
Code-check of steel plates according to Australian standards
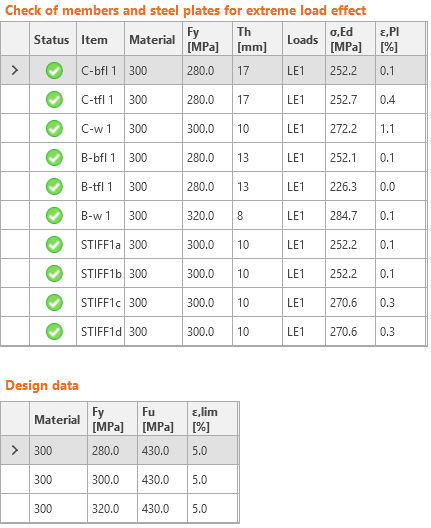
Strain check is performed at shell finite elements simulating plates. The yield strength is decreased by the capacity factor.
The resulting equivalent stress (HMH, von Mises) and plastic strain are calculated on plates. When the yield strength (multiplied by capacity factor ϕ = 0.9, which is editable in Code setup) on the bilinear material diagram is reached, the check of the equivalent plastic strain is performed. The limit value of 5 % is suggested in Eurocode (EN1993-1-5 App. C, Par. C8, Note 1). This value can be modified in the Code setup, but verification studies were made for this recommended value.
The plate element is divided into five layers, and elastic/plastic behavior is investigated in each of them. The program shows the worst result from all of them.
The CBFEM method can provide stress a little bit higher than yield strength. The reason is the slight inclination of the plastic branch of the stress-strain diagram, which is used in the analysis to improve the stability of the interaction calculation. This is not a problem for practical design. The equivalent plastic strain is exceeded at higher stress, and the joint does not satisfy anyway.
Code-check of bolts and preloaded bolts according to Australian standards
The forces in bolts including prying forces are determined by finite element analysis. The bolt resistances are checked by code provisions.
Bolts
Bolts are checked according to Chapter 9.2 Design of bolts. The tensile and shear force in each bolt is determined by finite element analysis. Prying forces are taken into account as suggested by Clause 9.1.8. Prying forces are determined by finite element analysis. Each shear plane is checked individually. Ply in the bearing is checked against the sum of shear forces at nearby planes.
Bolt in shear
A bolt subject to a design shear force is designed according to Cl. 9.2.2.1 and shall satisfy:
\[ V_f^* \le \phi V_f \]
where:
- Vf* – design shear force
- ϕ = 0.8 – capacity factor (Table 3.4) editable in Code setup
- Vf = 0.62 fuf A – nominal shear capacity of a bolt
- fuf – minimum tensile strength of the bolt as specified in Table 9.2.1
- A – area of a bolt equal either to Ac or Ao which are minor diameter area of the bolt as defined in AS 1275 or nominal plain shank area of the bolt, respectively. Each shear plane is checked individually.
The value of Ac is in the software approximated by a function:
Ac = 0.0000163 · As2 + 0.91682 · As − 0.85375
The maximal difference is 0.8 mm2 or 0.5 %.
Reduction factor given in Table 9.2.2.1 to account for the length of a bolted lap connection equals 1.0. The reduction is applied automatically by checking each bolt individually.
According to Cl. 9.2.2.5, for connections in which filler plates exceed 6 mm in thickness, the nominal shear capacity of a bolt shall be reduced by 15 %. For multi-shear plane connection, the reduction is applied to all shear planes.
Bolt in tension
A bolt subject to design tension force is designed according to Cl. 9.2.2.2 and shall satisfy:
\[ N_{tf}^* \le \phi N_{tf} \]
where:
- Ntf* – design tension force
- ϕ = 0.8 – capacity factor (Table 3.4) editable in Code setup
- Ntf = As fuf – nominal tensile capacity of a bolt
- As – tensile stress area of a bolt as specified in AS 1275
- fuf – minimum tensile strength of the bolt as specified in Table 9.2.1
Bolt subject to combined shear and tension
A bolt required to resist both design shear and design tensile forces at the same time is designed according to Cl. 9.2.2.3 shall satisfy:
\[ \left ( \frac{V_f^*}{\phi V_f} \right ) ^2 + \left ( \frac{N_{tf}^*}{\phi N_{tf}} \right ) ^2 \le 1.0 \]
where:
- ϕ = 0.8 – capacity factor (Table 3.4) editable in Code setup
Ply in bearing
A ply subject to a design bearing force due to a bolt in shear is designed according to Cl. 9.2.2.4 and shall satisfy:
\[ V_b^* \le ϕ V_b \]
where:
- ϕ = 0.9 – capacity factor (Table 3.4) editable in Code setup
- \( V_b = 3.2 d_f t_p f_{up} \le a_e t_p f_{up} \) – nominal bearing of a ply
- df – diameter of a bolt
- tp – thickness of the ply
- fup – tensile strength of the ply
- ae – minimum distance from the edge of a hole to the edge of a ply, measured in the direction of the component of a force, plus half the bolt diameter. The edge of a ply shall be deemed to include the edge of an adjacent bolt hole
Friction-type connections
For friction-type connections, the slip in serviceability limit state is required to be limited and designed according to Cl. 9.2.3. These bolts should be also checked as bearing type for ultimate limit state. A bolt subjected to shear force shall satisfy:
\[ V_{sf}^* \le ϕ V_{sf} \]
where:
- ϕ = 0.7 – capacity factor (Chapter 3.5.5) editable in Code setup
- Vsf = μ Nti kh – nominal shear capacity of a bolt
- μ = 0.35 – slip factor as specified in Clause 9.2.3.2 editable in Code setup
- Nti – minimum bolt tension at installation as specified in Clause 15.2.2.2
| Nominal diameter of bolt | Minimum bolt pretension [kN] |
| M16 | 95 |
| M20 | 145 |
| M24 | 210 |
| M30 | 335 |
| M36 | 490 |
| Other | \(A_s \cdot 600\) MPa |
- k h – factor for different hole types, as specified in Clauses 9.2.3.1 and 14.3.2
- k h = 1 for standard holes (+2 mm for d f ≤ 24 mm, +3 mm otherwise)
- k h = 0.85 for short slotted (hole length ≤ max(1.33 d f, d f + 10 mm)) and oversize holes
- k h = 0.70 for long slotted holes
Number of effective interfaces, nei, is always equal to 1, because each interface is checked separately.
Bolts in a friction-type connections loaded by combined shear and tension should satisfy:
\[ \left ( \frac{V_{sf}^*}{ϕ V_{sf}} \right ) + \left ( \frac{N_{tf}^*}{ϕ N_{tf}} \right ) \le 1.0 \]
where:
- Vsf* – design shear force on the bolt in the plane of the interfaces
- Ntf* – design tensile force on the bolt
- ϕ = 0.7 – capacity factor (Chapter 3.5.5) editable in Code setup
- Vsf – nominal shear capacity of the bolt
- Ntf = Nti – nominal tensile capacity of the bolt equal to minimum bolt tension at installation
Friction-type connections should be also checked for ultimate limit state. The bolt type should be changed to bearing – tension/shear interaction, the loads increased appropriately and the joint should be checked again.
Code-check of welds according to Australian standards
Fillet welds are checked according to AS 4100 - Chapter 9.6. The strength of CJP groove welds is assumed the same as the base metal and is not checked.
It is possible to set butt welds or fillet welds and along the full edge length, partial welds, or intermittent welds. Butt welds are assumed to have the same strength as the welded member and are not checked. In the case of fillet welds, the weld element is inserted between interpolation links connecting plates to each other. The weld element has a specified elasto-plastic material diagram to redistribute the stress along the weld length so that the long welds, multi-orientation welds or welding to unstiffened flange have similar resistance as according to hand calculation. The most stressed weld element is decisive in the weld check.
A fillet weld subject to a design force per unit length of weld, vw*, is designed according to Cl. 9.6.3.10 and shall satisfy:
\[ v_w^* \le ϕ v_w \]
where:
- ϕ = 0.8 – capacity factor (Chapter 3.4) editable in Code setup
- vw = 0.6 fuw tt – nominal capacity of a fillet weld per unit length
- fuw – nominal tensile strength of weld metal (Table 9.6.3.10 (A))
- tt – design throat thickness
The reduction factor, kr is assumed equal to 1 (weld shorter than 1.7 m).
The weld diagrams show stress according to the following formula:
\[ \sigma = \sqrt{ \sigma_{\perp}^2 + \tau_{\perp}^2 + \tau_{\parallel}^2 } \]
Code-check of concrete block according to Australian standards
Concrete below base plate is simulated by Winkler subsoil with uniform stiffness, which provides the contact stresses. The average stress at the loaded area in contact with base plate is used for compressive check.
Concrete bearing surface
Concrete bearing surface is checked according to AS3600: 2018 – Cl. 12.6. The design bearing stress at a concrete surface shall not exceed:
\[ ϕ f_b = ϕ 0.9 f'_c \sqrt{\frac{A_2}{A_1}} \le ϕ 1.8 f'_c \]
where:
- ϕ = 0.6 – capacity factor (Table 2.2) editable in Code setup
- f'c – characteristic compressive cylinder strength of concrete at 28 days
- A1 – bearing area
- A2 – largest area of the supporting surface that is geometrically similar and concentric with A1. The side slopes of the frustum are 1 longitudinally and 2 transversally with respect to the direction of the load.
The design bearing stress, σ, equals to the average stress under the base plate on the area below the base plate in contact with concrete.
Transfer of shear
The shear action at the base plate is assumed to be transferred from the column to the concrete foundation by:
- Friction between base plate and concrete / grout
- Shear lug
- Anchor bolts
Shear force transfer by friction
The shear capacity is calculated according to Gianluca Ranzi, Peter Kneen: Design of Pinned Column Base Plates, Journal of the Australian Steel Institute, vol. 36, no. 2, September 2002 – Chapter 6.5.3 as follows:
\[ ϕ V_f = ϕ μ N_c^* \]
where:
- ϕ = 0.8 – capacity factor
- μ = 0.55 – coefficient of friction editable in Code setup
- Nc* – column design axial compression load
Shear force transfer by shear lug
If shear force is transferred by the shear lug, the shear lug is modeled by finite elements, and its plates and welds are checked by the finite element method and weld components. Additional checks are required – bearing concrete strength; concrete edge strength.
Bearing concrete strength
The bearing strength of concrete is checked according to Gianluca Ranzi, Peter Kneen: Design of Pinned Column Base Plates, Journal of the Australian Steel Institute, vol. 36, no. 2, September 2002 – Chapter 6.5.5:
\[ ϕ_c V_b = 0.85 ϕ_c f'_c A_{sl} \]
where:
- ϕc = 0.6 – capacity factor for concrete in bearing editable in Code setup
- f'c – characteristic compressive cylinder strength of concrete at 28 days
- Asl – projected area of the embedded shear lug in the direction of the force, excluding the portion of the lug in contact with the grout above the concrete member
Concrete edge strength
If a shear force is acting against a free concrete edge it should be verified that the concrete is able to carry the applied shear action. The concrete edge strength is checked according to Gianluca Ranzi, Peter Kneen: Design of Pinned Column Base Plates, Journal of the Australian Steel Institute, vol. 36, no. 2, September 2002 – Chapter 6.5.5:
\[ ϕ V_{ce} = ϕ 0.33 \sqrt{f'_c} A_{Vc} \]
where:
- ϕ =0.85 – capacity factor
- f'c – characteristic compressive cylinder strength of concrete at 28 days
- AVc – effective stress area defined by projecting a 45° plane from the bearing edges of the shear lug to the free surface in the direction of the shear load. The bearing area of the shear lug is excluded from the projected area
Shear force transfer by anchors
The shear force is assumed to be transferred by anchors. Force in each anchor is determined by finite element method. Each anchor or anchor group is checked for steel failure in shear, concrete edge failure, concrete pry-out failure, and combined tension and shear loading if tension is also present.
Code-check of anchors according to Australian standards
The forces in anchors including prying forces are determined by finite element analysis, but the resistances are checked using code provisions of AS 5216.
The check of anchors is provided according to AS 5216:2018. Although the code does not specifically provide some formulas for cast-in anchors, the formulas are the same as in SA TS 101:2015 where cast-in anchors are specifically mentioned. Cracked or uncracked concrete can be selected in Code setup. Cracked concrete is conservatively assumed as default. Concrete cone breakout check in tension and shear may be disregarded in Code setup, which means the force is assumed to be transferred via reinforcement. User is provided with the magnitude of this force. Due to the use of concrete cone breakout resistance in the formula in concrete pry-out failure check, this check is also disregarded.
Following checks of anchors loaded in tension are not provided and should be checked using information in relevant Technical Product Specification (testing according to AS 5216:2018: Appendix A):
- Pull-out failure of fastener (for post-installed mechanical anchors) – AS 5216:2018: 6.2.4,
- Combined pull-out and concrete cone failure (for post-installed bonded anchors) – AS 5216:2018: 6.2.5,
- Concrete splitting failure – AS 5216:2018: 6.2.6.
Concrete blow-out failure is provided only for anchors with washer plates.
Steel failure in tension
Steel failure in tension is checked according to Cl. 6.2.2:
\[ ϕ_{Ms} N_{tf} = ϕ_{Ms} A_s f_{uf} \]
where:
- \( ϕ_{Ms} = \frac{5 f_{yf}}{6 f_{uf}} \le 1/1.4 \) – capacity factor for steel failure in tension (Table 3.2.4)
- As – tensile stress area of a bolt as specified in AS 1275
- fuf – minimum tensile strength of the bolt as specified in AS 4100 – Table 9.3.1
Concrete cone failure
Concrete cone failure is checked according to Cl. 6.2.3 and is provided for the group of anchors (where applicable). The characteristic strength of the tensioned fasteners in a group or a single fastener is:
\[ ϕ_{Mc} N_{Rk,c} = ϕ_{Mc} N_{Rk,c}^0 \left ( \frac{A_{c,N}}{A^0_{c,N}} \right ) \psi_{s,N} \psi_{re,N} \psi_{ec,N} \psi_{M,N} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( N_{Rk,c}^0 = k_1 \sqrt{f'_c} h_{ef}^{1.5} \) – characteristic strength of a fastener, remote from the effects of adjacent fasteners or edges of the concrete member – Cl. 6.2.3.2
- Ac,N – actual projected area of the failure cone of the fastener that is limited by adjacent fasteners and edges of the concrete member – Cl. 6.2.3.3
- Ac,N0 = scr,N2 – reference projected area of a single fastener with an edge distance at least equal to 1.5 hef – Cl. 6.2.3.3
- \( \psi_{s,N} = 0.7 + 0.3 \frac{c}{c_{cr,N}} \le 1 \) – parameter related to the distribution of stresses in the concrete due to the proximity of the fastener to an edge of the concrete member – Cl. 6.2.3.4
- \( \psi_{re,N} = 0.5 + \frac{h_{ef}}{200} \le 1 \)– parameter accounting for the shell spalling effect – Cl. 6.2.3.5
- \( \psi_{ec,N} = \frac{1}{1+2 e_N / s_{cr,N}} \le 1 \) – parameter accounting for eccentricity of the resultant load in a fastener group – Cl. 6.2.3.6
- \( \psi_{M,N} = 2- \frac{2 z}{3 h_{ef}} \ge 1 \) – parameter accounting for the effect of a compression force between the fixture and concrete – Cl. 6.2.3.7; this parameter is equal to 1 if c < 1.5 hef or the ratio of the compressive force (including the compression due to bending) to the sum of tensile forces in anchors is smaller than 0.8
- \item k1 – parameter; for cast-in anchors (Anchor type – washer plates) k1 = kcr,N = 8.9 for cracked concrete and k1 = kucr,N = 12.7 for uncracked concrete; for post-installed anchors (Anchor type – straight) k1 = kcr,N = 7.7 for cracked concrete and k1 = kucr,N = 11.0 for uncracked concrete
- scr,N = 2 ccr,N = 3 hef – spacing of fasteners
- ccr,N = 1.5 hef – characteristic edge distance
- hef – effective embedment depth of the fastener, in case of narrow concrete member, Cl. 6.2.3.8 applies and\( h'_{ef} = \max \left ( \frac{c_{max}}{c_{cr,N}}h_{ef}; \, \frac{s_{max}}{s_{cr,N}}h_{ef} \right ) \)
- z – internal lever arm
- c – smallest edge distance
The concrete breakout cone area for group of anchors loaded by tension that create common concrete cone, Ac,N, is shown by red dashed line.
Pull-out failure
Pull-out failure is checked for cast-in headed fasteners (Anchor type – washer plate) according to SA TS 101:2015 – Cl. 6.2.3:
\[ ϕ_{Mc} N_{Rk,p} = k_1 A_h f'_c \]
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- k1 –parameter relating to the state of the concrete; for cracked concrete k1 = 8.0, for uncracked concrete k1 = 11.2
- Ah – area of the load-bearing head of the fastener; for circular washer plate \( A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right \)$, for rectangular washer plate \( A_h = a_{wp}^2 - \frac{\pi}{4} d^2 \)
- dh ≤ 6 th + d – diameter of head of fastener
- th – thickness of the head of the headed fastener
- d – diameter of the shank of the fastener
- awp – length of the edge of the rectangle washer plate
- f'c – characteristic compressive strength of concrete
The pull-out failure for other than cast-in headed anchors is not calculated and the resistance should be guaranteed by a manufacturer or determined by testing and assessment in accordance with Appendix A.
Neither resistance to splitting failure during installation (Cl. 6.2.6.1) nor due to loading (Cl. 6.2.6.2) is provided and should be guaranteed by a manufacturer or determined by testing and assessment in accordance with Appendix A.
Blow-out failure
Blow-out failure is checked for headed anchors (Anchor type – washer) with edge distance c ≤ 0.5 hef according to Cl. 6.2.7. Anchors are treated as a group if their spacing near the edge is s ≤ 4 c1. Undercut anchors can be checked the same way but the value of Ah is unknown in the software. The blow-out failure of undercut anchors can be determined by selecting washer plate with the corresponding dimension.
\[ ϕ_{Mc} N_{Rk,cb} = ϕ_{Mc} N_{Rk,cb}^0 \frac{A_{c,Nb}}{A_{c,Nb}^0} \psi_{s,Nb} \psi_{g,Nb} \psi_{ec,Nb} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( N_{Rk,cb}^0 = k_5 c_1 \sqrt{A_h} \sqrt{f'_c} \) – characteristic strength of a single fastener remote from the effects of adjacent fasteners and edges of the concrete member – Cl. 6.2.7.2
- Ac,Nb – actual projected area for the fastener that is limited by the edges of the concrete member (c2 ≤ 2 c1, the presence of adjacent fasteners (s ≤ 4 c1) or the member thickness – Cl. 6.2.7.3
- Ac,Nb0 = (4 c1)2 – reference projected area of a single fastener with an edge distance equal to c1 – Cl. 6.2.7.3
- \( \psi_{s,Nb} = 0.7+0.3 \frac{c_2}{2 c_1} \le 1 \) – parameter accounting for the disturbance of stresses in the concrete due to the close proximity of the fastener to a corner of the concrete member – Cl. 6.2.7.4
- \( \psi_{g,Nb} = \sqrt{n} + (1-\sqrt{n}) \frac{s_2}{4c_1} \ge 1 \) – parameter accounting for a group effect – Cl. 6.2.7.5
- \( \psi_{ec,Nb} = \frac{1}{1+2 e_N / s_{cr,Nb}} \le 1 \) – parameter accounting for eccentricity of loading on a fastener group – Cl. 6.2.7.6
- k5 – parameter related to the state of the concrete; for cracked concrete k5 = 8.7, for uncracked concrete k5 = 12.2
- c1 – edge distance of fastener in direction 1 towards the closest edge
- c2 – edge distance of fastener perpendicular to direction 1 that is the smallest edge distance in a narrow member with multiple edge distances
- Ah – area of the load-bearing head of the fastener; for circular washer plate \( A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right \), for rectangular washer plate \( A_h = a_{wp}^2 - \frac{\pi}{4} d^2 \)
- f'c – characteristic compressive strength of concrete
- n – number of fasteners in a row parallel to the edge of the concrete member
- s2 – spacing of fasteners in a group perpendicular to direction 1
- scr,Nb = 4 c1 – spacing that is required for a fastener to develop its characteristic tensile strength against blow-out failure
According to Cl. 6.2.8, the supplementary reinforcement may be used to transfer forces causing concrete blow-out failure. Such reinforcement should be designed in accordance with AS 3600.
Steel failure in shear
Steel failure in shear is determined according to Cl. 7.2.2. It is assumed that the anchor is made of threaded rod with the same material properties as bolts.
Shear force without lever arm
Shear force without lever arm is assumed if stand-off – direct is selected. It is assumed that fasteners are from ductile steel and factor k7 = 1. Each fastener is checked separately. The resistance is determined according to AS 5216 – Cl. 7.2.2.2 and AS 4100 – Cl. 9.2.2.1:
\[ ϕ_{Ms} V_{Rk,s} = ϕ_{Ms} 0.62 f_{uf} A \]
where:
- \( ϕ_{Ms} = f_{yf} / f_{uf} \le 0.8 \) when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- fuf – minimum tensile strength of the bolt as specified in AS 4100 Table 9.2.1
- A – area of a bolt equal either to Ac or Ao which are minor diameter area of the bolt as defined in AS 1275 or nominal plain shank area of the bolt, respectively
For fasteners with hef / d < 5 in concrete having f’c < 20 MPa, VRk,s is multiplied by a factor equal to 0.8.
Shear force with lever arm
Steel shear strength with lever arm is calculated according to Cl. 7.2.2.3:
\[ ϕ_{Ms} V_{Rk,s,M} = ϕ_{Ms} \frac{\alpha_M M_{Rk,s}}{l_a} \]
where:
- \( ϕ_{Ms} = f_{yf} / f_{uf} \le 0.8 \) when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- αM = 2 – parameter accounting for the degree of restraint, fixture is assumed to be prevented from rotating – Cl. 4.2.2.4
- \( M_{Rk,s} = M_{Rk,s}^0 \left ( 1- \frac{N^*}{ϕ_{Ms} N_{Rk,s}} \right ) \) – characteristic flexural strength of the fastener influenced by the axial load
- la = a3 + e1 – length of the lever arm
- a3 = 0.5 d – distance between the assumed point of restraint of the fastener loaded in shear and the surface of the concrete
- e1 = tg + tfix / 2 – eccentricity of the applied shear load relative to the concrete surface, neglecting the thickness of a levelling grout or mortar
- tg – thickness of grout layer
- tfix – thickness of base plate
- d – nominal diameter of the fastener
- N* – design tension load
- ϕMs NRk,s – tensile strength of a fastener to steel failure
- MRk,s0 = 1.2 Wel fuf – characteristic flexural strength of the fastener – ETAG 001 – Annex C
- Wel = π d3 / 32 – elastic section modulus of the fastener, the diameter reduced by threads, \( d_s = \sqrt{\frac{4 A_s}{\pi}} \), is used instead of nominal diameter, d, if Shear plane in thread is selected
Concrete edge failure
Concrete edge failure is checked according to Cl. 7.2.3. If concrete cones of fasteners intersect, they are checked as a group. The edges in the direction of the shear load are checked. All load at a base plate is presumed to be transferred by a fastener near the checked edge.
\[ ϕ_{Mc} V_{Rk,c} = ϕ_{Mc} V_{Rk,c}^0 \frac{A_{c,V}}{A_{c,V}^0} \psi_{s,V} \psi_{h,V} \psi_{ec,V} \psi_{\alpha,V} \psi_{re,V} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( V_{Rk,c}^0 = k_9 d^{\alpha} l_f^{\beta} \sqrt{f'_c} c_1^{1.5} \) – initial value of the characteristic shear strength of the fastener – Cl. 7.2.3.2
- Ac,V – actual area of idealised concrete break-out body – Cl. 7.2.3.3
- Ac,V0 = 4.5 c12 – reference projected area of failure cone – Cl. 7.2.3.3
- \( psi_{s,V} = 0.7 + 0.3 \frac{c_2}{1.5 c_1} \le 1 \) – parameter accounting for the disturbance to the distribution of stresses in the concrete member – Cl. 7.2.3.4
- \( \psi_{h,V} = \left ( \frac{1.5 c_1}{h} \right ) ^{0.5} \ge 1 \) – parameter accounting for the influence of member thickness – Cl. 7.2.3.5
- \( \psi_{ec,V} = \frac{1}{1+2 e_V / (3c_1)} \le 1 \) – parameter accounting for the eccentricity of the resultant load in a fastener group – Cl. 7.2.3.6
- \( \psi_{\alpha,V} = \sqrt{\frac{1}{(\cos \alpha_V)^2 + (0.5 \sin \alpha_V)^2}} \ge 1 \) – parameter accounting for the angle of the applied load – Cl. 7.2.3.7
- ψre,V = 1 – parameter accounting for the shell spalling effect – Cl. 7.2.3.8, no edge reinforcement or stirrups are assumed
- k9 – parameter accounting for the state of the concrete; for cracked concrete k9 = 1.7, for uncracked concrete k9 = 2.4
- d – nominal diameter of the fastener
- \( \alpha = 0.1 \left ( \frac{l_f}{c_1} \right ) ^{0.5} \)
- \( \beta = 0.1 \left ( \frac{d}{c_1} \right ) ^{0.2} \)
- lf = hef ≤ 12 d where d ≤ 24 mm; lf = hef ≤ max (8 d, 300 mm) where d > 24 mm – parameter related to the length of the fastener
- f'c – characteristic compressive cylinder strength of concrete at 28 days
- c1 – edge distance of fastener to the investigated edge; according to Cl. 7.2.3.9, for a narrow member, c2,max < 1.5 c1 that is also deemed to be thin, h < 1.5 c1, c'1 is used in previous equations instead of c1; the reduced c'1 = max (c2,max / 1.5, h/ 1.5, sc,max / 3)
- c2 – the smaller edge distance of fastener in the direction perpendicular to the investigated edge
- h – concrete member thickness
- eV – eccentricity of the resultant shear force acting on a group of fasteners relative to the centre of gravity of the fasteners loaded in shear
- αV – angle between the applied load to the fastener or fastener group and the direction perpendicular to the free edge under consideration, 0° < αV < 90°
- hef – effective embedment depth of the fastener
Concrete pry-out failure
Concrete pry-out failure is checked according to Cl. 7.2.4. All anchors at one base plate are assumed to be loaded in shear and the concrete breakout resistance, NRk,c, used in the calculation, is calculated with the assumptions of all anchors loaded in tension without any eccentricity. No supplementary reinforcement is assumed.
\[ ϕ_{Mc} V_{Rk,cp} = ϕ_{Mc} k_8 N_{Rk,c} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- k8 – parameter published in the Report of Assessment, according to ETAG 001 – Annex C, for hef < 60 mm, k8 = 1 and for hef ≥ 60 mm, k8 = 2
- NRk,c – characteristic concrete cone strength for a single fastener or fastener in a group
Combined tension and shear loading
The resistance of a fastener loaded by combined tension and shear is determined according to Chapter 8.
Steel failure
An assessment of the performance under combined tension and shear loading of the fastener is based on AS 4100:
\[ \left ( \frac{N^*}{ϕ_{Ms} N_{Rk,s}} \right ) ^2 + \left ( \frac{V^*}{ϕ_{Ms} V_{Rk,s}} \right ) ^2 \le 1.0 \]
Concrete failure
Failure modes other than steel are checked according to Cl. 8.2.1:
\[ \left ( \frac{N^*}{ϕ_{Mc} N_{Rk,i}} \right ) ^{1.5} + \left ( \frac{V^*}{ϕ_{Mc} V_{Rk,i}} \right ) ^{1.5} \le 1.0 \]
where:
- N* – design tension force applied to a single fastener or group
- V* – design shear force applied to a single fastener or group
- NRk,i – characteristic tensile strength of fastener or group to failure mode ‘i’
- VRk,i – characteristic shear strength of fastener or group to failure mode ‘i’
- \( ϕ_{Ms} = \frac{5 f_{yf}}{6 f_{uf}} \) – capacity factor for steel failure in tension (Table 3.2.4)
- ϕMs = fyf / fuf ≤ 0.8 when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
Stand-off anchors
Anchors with stand-off are designed as beam member according to AS 4100 with capacity factors of bolts. The assumed length of the member is the sum of the height of gap, half of nominal diameter thickness and half of the base plate thickness. Stand-off anchors are usually checked as a construction stage before grouting.
Bending capacity
Bending capacity is determined according to AS 4100, Cl. 5.1.
M* ≤ ϕ Ms
where:
- M* – bending moment acting on anchor determined by finite element method
- ϕ = 0.8 – capacity factor for bolts
- Ms = fy Ze – section moment capacity for bending
- fy – anchor yield strength
- Ze = min {S, 1.5 · Z} – effective section modulus – Cl. 5.2.3
- \( S = \frac{d^3}{6} \) – plastic section modulus; if Shear plane in thread is selected, nominal diameter d is replaced by diameter reduced by threads, ds
- \( Z = \frac{1}{32} \pi d^3 \) – elastic section modulus; if Shear plane in thread is selected, nominal diameter d is replaced by diameter reduced by threads, ds
Shear capacity
Shear capacity is determined according to AS 4100, Cl. 5.11.
V* ≤ ϕ Vw
where:
- V* – design shear force
- ϕ = 0.8 – capacity factor for bolts
- Vw = 0.6 fy Aw – nominal shear yield capacity – Cl. 5.11.4
- fy – anchor yield strength
- Aw = 0.844 As – shear area
- As – tensile stress area of a bolt as defined in AS 1275
Axial compression capacity
Axial compression capacity is determined according to AS 4100, Cl. 6. Buckling is taken into account according to Cl. 6.3:
N* ≤ ϕ Nc
where:
- N* – design compressive force
- ϕ = 0.8 – capacity factor for bolts
- Nc = αc Ns ≤ Ns – nominal member capacity – Cl. 6.3.3
- Ns = kf As fy – nominal section capacity – Cl. 6.2
- fy – anchor yield strength
- le = ke l – effective length – Cl. 6.3.2
- ke = 2 – member effective length factor, it is assumed conservatively that the anchor is fixed and the bottom and pinned at the top as sway member
- l = lgap + d / 2 + tp / 2 – assumed length of the member
- lgap – gap height
- d – nominal bolt diameter
- tp – base plate thickness
- \( \alpha_c = \xi \left \{ 1 - \sqrt{1- \left ( \frac{90}{\xi \lambda} \right )^2 } \right \} \) – compression member slenderness reduction factor – Cl. 6.3.3
- \( \xi = \frac{\left( \frac{\lambda}{90} \right)^2 + 1 + \eta}{2 \left( \frac{\lambda}{90} \right)^2} \) – compression member factor – Cl. 6.3.3
- \( \lambda = \lambda_n + \alpha_a \alpha_b \) – slenderness ratio – Cl. 6.3.3
- \( \eta = 0.00326 (\lambda-13.5) \) – compression member imperfection factor – Cl. 6.3.3
- \( \lambda_n = \frac{l_e}{r} \sqrt{k_f} \sqrt{\frac{f_y}{250}} \) – modified compression member slenderness – Cl. 6.3.3
- kf = 1 – form factor – Cl. 6.2.2
- \( r = \sqrt{\frac{I_s}{A_s}} \) – radius of gyration
- \( I_s = \frac{1}{64} \pi d_s^4 \) – moment of inertia
- As – tensile stress area of a bolt as defined in AS 1275
- \( d_s = \sqrt{\frac{4 A_s}{\pi}} \) – diameter reduced by threads
- \( \alpha_a = \frac{2100 (\lambda_n - 13.5)}{\lambda_n^2 - 15.3 \lambda_n + 2050} \) – compression member factor – Cl. 6.3.3
- αb = 0.5 – compression member section constant - Table 6.3.3
Axial tension capacity
Axial tension capacity is determined according to AS 4100, Cl. 7:
N* ≤ ϕ Nt
where:
- N* – design tensile force
- ϕ = 0.8 – capacity factor for bolts
- Nt = As fy – nominal section capacity of a bolt in tension – Cl. 7.2
- As – tensile stress area of a bolt as specified in AS 1275
- fy – anchor yield strength
Interaction of loading
If an anchor with stand-off is loaded by shear load and the compressive force, check of interaction of loading is performed:
\[ \frac{N^*}{\phi N_c} + \frac{M^*}{\phi M_s} \le 1 \]
where:
- N* – design compressive force
- ϕ = 0.8 – capacity factor for bolts
- Nc – compressive resistance
- M* – design bending moment due to shear on a lever arm
- Ms – bending resistance
Additionally, the checks of steel shear failure and concrete shear failures (concrete edge failure, concrete pryout failure) are performed.
If an anchor with stand-off is loaded by shear load and tensile force, check of interaction of loading is performed:
\[ \frac{N_{tf}^*}{\phi N_{t}} + \frac{M^*}{\phi M_s} \le 1 \]
where:
- N*tf – design tensile force
- ϕ = 0.8 – capacity factor for bolts
- Nt – tensile resistance
- M* – design bending moment due to shear on a lever arm
- Ms – bending resistance
Additionally, the checks of steel shear failure and concrete failures due to tension and shear are performed.
Detailing of bolts, welds and anchors according to Australian standards
Bolts
Minimum pitch (distance between centres of bolt holes) shall not be less than 2.5 times the nominal bolt diameter. The value is recommended in Clause 9.5.1 and is editable in Code setup.
Minimum edge distance (distance between centre of the bolt hole to the plate edge) shall not be less than 1.25 times the nominal bolt diameter. The value is recommended in Clause 9.5.2 for rolled edges and can be modified in Code setup.
Welds
Minimum size of a fillet weld is checked according to Clause 9.6.3.2 and should be the lesser of the thinner part joined thickness and the value in the following table:
The weld size is assumed as \( \sqrt{2} \) times the weld throat thickness.
Anchors
Minimum spacing between anchors should be s ≥ 4d where d is nominal diameter of the anchor. The factor 4 is editable in Code setup.
Minimum edge distance follows the rules for bolts, i.e. it shall not be less than 1.25 times the nominal bolt diameter. The value is recommended in Clause 9.5.2 for rolled edges and can be modified in Code setup.
Joint classification according to Australian standards
Joints are classified according to joint stiffness to:
- Rigid – joints with insignificant change of original angles between members,
- Semirigid – joints which are assumed to have the capacity to furnish a dependable and known degree of flexural restraint,
- Simple – joints which do not develop bending moments.
Australian standard AS 4100, Cl. 4.2 does not provide exact boundaries so the joints are classified according to the commentary in AISC 360-16, Cl. B3.4.
- Rigid – \( \frac{S_{j,ini} L_b}{E I_b} \ge 20 \)
- Semirigid – \( 2 < \frac{S_{j,ini} L_b}{E I_b} < 20 \)
- Simple – \( \frac{S_{j,ini} L_b}{E I_b} \le 2 \)
where:
- Sj,ini – initial stiffness of the joint; the joint stiffness is assumed linear up to the 2/3 of Mj,Rd
- Lb – theoretical length of the analyzed member
- E – Young's modulus of elasticity
- Ib – moment of inertia of the analyzed member
- Mj,Rd – joint design moment resistance
Capacity design according to Australian standards
Capacity design is a part of seismic check and ensures that the joint has sufficient deformation capacity.
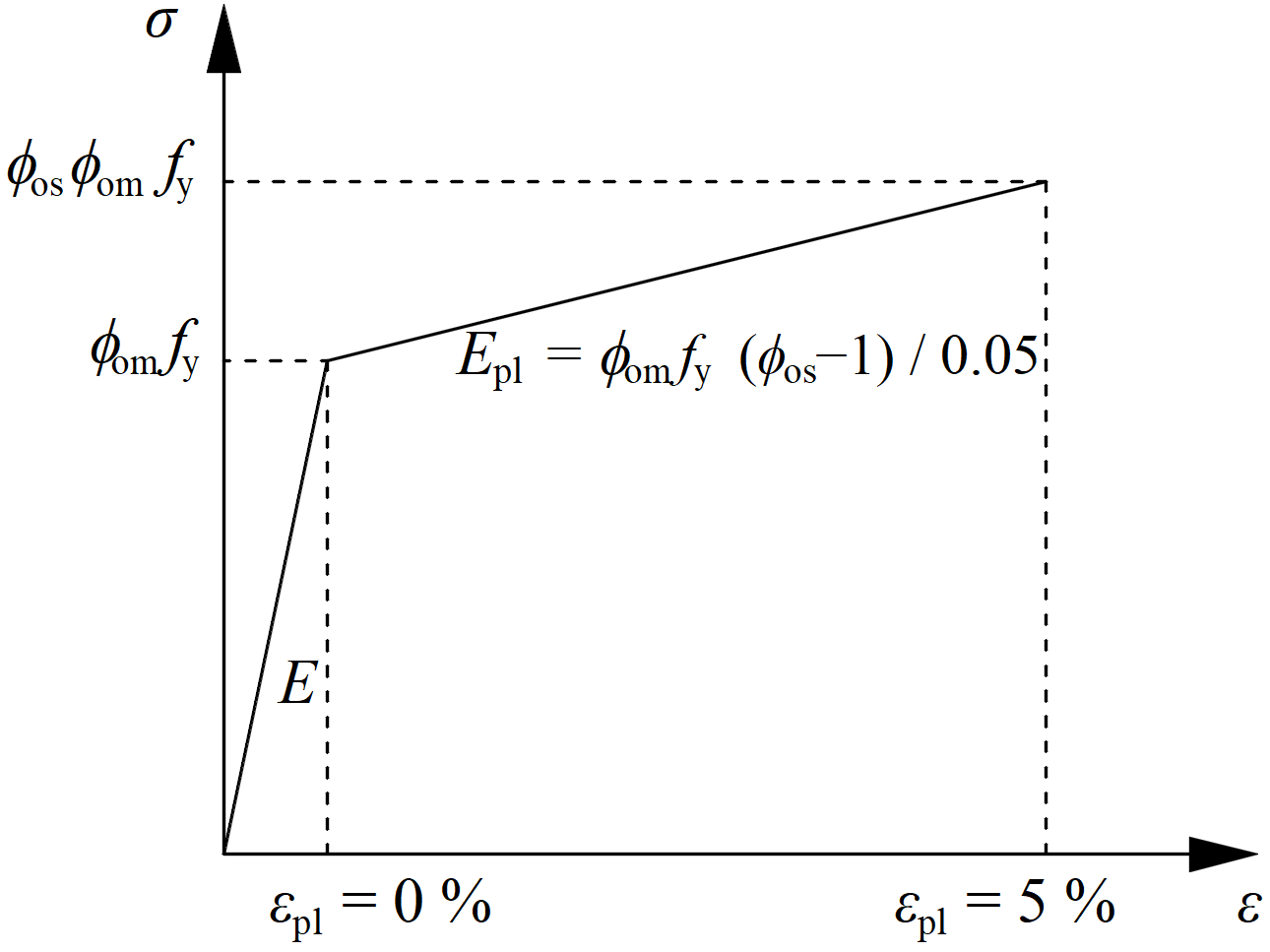
The objective of capacity design is to confirm a building undergoes controlled ductile behavior in order to avoid collapse in a design-level earthquake. Capacity design is missing in Australian standard so New Zealand standard is used instead. Plastic hinge is expected to appear in dissipative item and all non-dissipative items of the joint must be able to safely transfer forces due to the yielding in the dissipative item. The dissipative item is usually a beam in moment resisting frame but it may also be e.g. an end plate. The safety factor is not used for dissipative items. The yield strength of the dissipative item is calculated as Fy,max = 0.9 ϕos ϕomfy, where:
- ϕos – strain-hardening factor; the recommended values are ϕos = 1.15 for beam in moment resisting frame, γsh = 1.0 otherwise; editable in operation
- ϕom – overstrength factor – EN 1998-1, Cl. 6.2; the recommended value is ϕom = 1.3; editable in materials
The material diagram is modified according to the following figure:
The increased strength of the dissipative item allows for the input of loads that cause the plastic hinge to appear in dissipative item. In the case of moment resisting frame and beam as the dissipative item, the beam should be loaded by My = fy,maxWpl,y and corresponding shear forceVz = –2 My / Lh, where:
- fy – characteristic yield strength
- Wpl,y – plastic section modulus
- Lh – distance between plastic hinges on the beam
In case of asymmetric joint, the beam should be loaded by both sagging and hogging bending moments and their corresponding shear forces.
The plates of dissipative items are excluded from check.