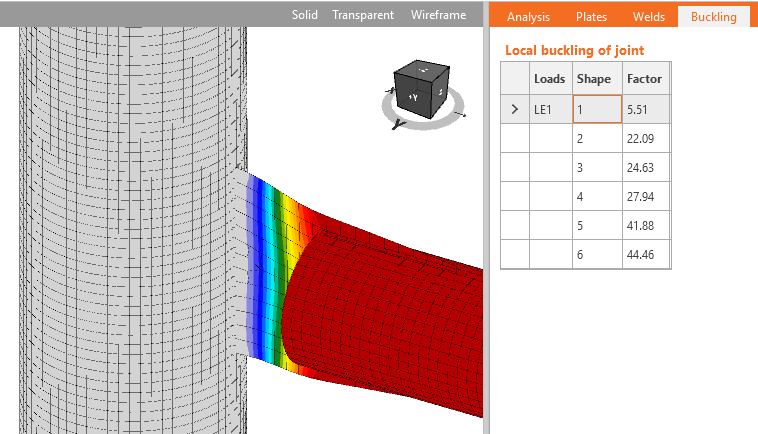
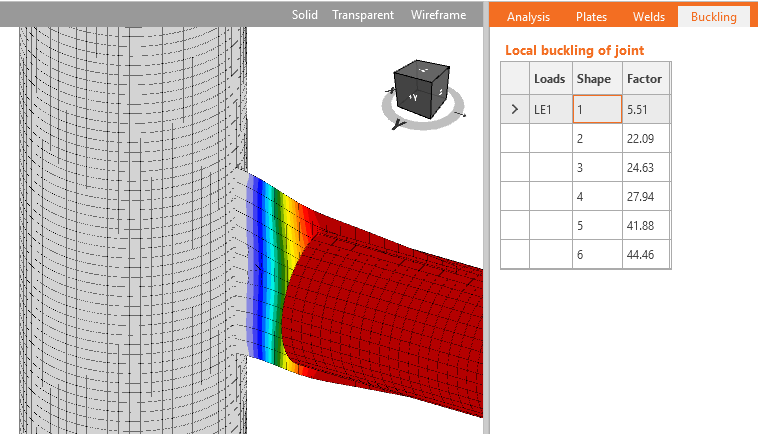
IDEA StatiCa Connection allows users to perform linear buckling analysis to confirm the safety of using plastic analysis. The result of linear buckling analysis is buckling factor αcr corresponding to the buckling mode shape. The buckling factor is the multiplicator of set load when Euler’s critical load of a perfect structure is reached. E.g. elastic critical buckling load Pe is determined by:
- loading a column by compressive force P
- performing linear buckling analysis, selecting most critical buckling mode (usually the first) and buckling factor αcr
- multiplying compressive force by buckling factor, i.e. Pe = P × αcr
AISC codes use mostly critical slenderness to limit the thickness of plates.
The critical slenderness can be expressed by critical buckling factor using following formulas:
where:
- λ – plate slenderness
- KL – effective length
- r – radius of gyration
- – plate relative slenderness
- – minimum load amplifier for the design loads to reach the characteristic value of resistance of the most critical cross-section, neglecting any plate buckling and lateral-torsional buckling; for load equal to plate plastic resistance,
- E – Young’s modulus of elasticity
- Fy – yield strength
A linear buckling analysis can determine the elastic buckling load, expressed as a ratio of the applied load. While providing useful information that can guide design, the linear buckling analysis does not consider potential yielding that can reduce stiffness and the buckling load (i.e., inelastic buckling), nor does it consider the effects of initial geometric imperfections. Because of these limitations, to use IDEA StatiCa, the connection needs to be stocky enough that neither elastic buckling nor inelastic buckling will occur. The elastic buckling load ratio provides a convenient measure of stockiness (or slenderness).
Elements of connections that are slender enough for inelastic buckling to occur still have strength, potentially enough strength for a given application. However, without the capability to accurately quantify inelastic buckling strength in IDEA StatiCa, these cases should be avoided or evaluated using different methods.
General recommendation - (Global buckling)
In AISC 360-16 – J.4, it is stated that plastic resistance may be used if λ = KL/r ≤ 25. Then e.g. for steel A36 the corresponding buckling factor is equal to 12.7. Note that for stronger steel, the corresponding buckling factor decreases. That means if the buckling factor is higher than 12.7, plastic resistance may be safely used. If the buckling factor is smaller, provisions of Chapter E apply.
Steel with Fy=50 ksi
Summary of the global buckling limiting factors
| Steel Fy | AISC Design Method | Critical buckling factor |
| 36 ksi | LRFD | 12.7 |
| 50 ksi | LRFD | 9.16 |
| 36 ksi | ASD | 21 |
| 50 ksi | ASD | 15 |
This limit is very strict and applies generally for all types of plates. It was derived from Dowswell’s research into stability of gusset plates. For gusset plates or connecting plates directly affecting the buckling of connected member, this limit should be used.
Gusset plates are identified in the global buckling category, but the stability of the gusset plate depends on how many edges are restrained.
One side restrained - Global limit factors.
Two/three sides restrained - local limit factors
Stiffening plates in the joint (local buckling)
However, for plates in the joint, e.g. stiffeners, haunches, column web panel, the limiting buckling factor may be much smaller using the provisions of Chapter E or corresponding chapters in design guides. A few examples are presented:
Limiting width to thickness ratio λr from AISC 360-16, Table B4.1a for web of built-up I section, flange of built-up I section and wall of rectangular hollow section:
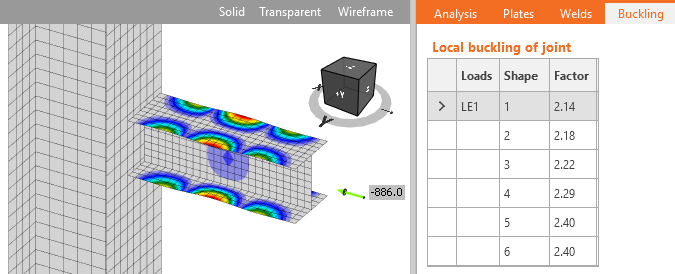
In the software, the length of the standard member was set to 3 and the length of the member with hollow section to 4 to enable the development of local buckling. For these examples, the stiff support for investigated members is necessary and therefore, the strong column fixed on both ends was used. The limiting width-to-thickness ratio is set to the investigated plate. The member is loaded to its compressive resistance. The buckling analysis is performed and the lowest buckling factor corresponding to the buckling mode shape for the investigated plate is noted. Other plates in the model are thick so the first buckling mode is relevant. The plate is considered non-slender and its full width can be used. Higher plate thickness leads to a higher buckling factor.
| E = | 29000 | ksi | Young's modulus of elasticity | |
| Fy = | 36 | ksi | yield strength | |
| ΦFy= | 32.4 | ksi | Factored yield strength | |
| Fcr = | 32.4 | ksi | critical stress | E3 or E4 |
Web of built-up I section
| h = | 7.01 | in | width of the element | |
| tw = | 0.1614 | in | thickness | |
| h/tw = | 43.4 | width-to-thickness ratio for the element | B4.1 | |
| λr = | 44.6 | limiting width-to-thickness ratio | Table B4.1a |
Flange of built-up I section
| b = | 3.74 | in | width of the element | |
| t = | 0.1850 | in | thickness | |
| b/t = | 20.2 | width-to-thickness ratio for the element | B4.1 | |
| λr = | 19.4 | limiting width-to-thickness ratio | Table B4.1a |
Wall of RHS
| b = | 7.08 | in | width of the element | |
| t = | 0.1693 | in | thickness | |
| b/t = | 41.9 | width-to-thickness ratio for the element | B4.1 | |
| λr = | 41.9 | limiting width-to-thickness ratio | Table B4.1a |
Triangular haunch
Thickness limitation according to AISC DG4 - 3.16 and AISC 358-18 – 6.8.1 – Step 9:
The beam was loaded by a bending moment so that the plate was at its limit compressive strength and then performing linear buckling analysis.
End plate stiffener
| hst = | 5.511 | in | stiffener height | |
| ts = | 0.33 | mm | stiffener thickness | AISC DG4 - 3.16 |
The limits in AISC codes correspond for these examples to buckling factor around 3. For experimental research into slender compressed plates in connection, see the research papers.
Bracket plates
A research study was performed to develop practical design guidelines for the buckling strength of bracket plates that can be implemented with Local Buckling Analysis and Material Nonlinear Analysis.
- For the 86 specimens, the design method in the 15th Edition AISC Manual was conservative
- The results showed that accurate results can be achieved with the finite element method by combining MNA with LBA.
- To avoid buckling, the critical load, Pel, based on LBA, must be equal to or greater than 4Pr for LRFD design and 6Pr for ASD design.
Summary of the local buckling limiting factors
| AISC Design method | Critical buckling factor |
| LRFD | αcr>3 – Member platesαcr>4 – Connection plates (i.e. bracket plates) |
| ASD | αcr>4.5 – Member platesαcr>6 – Connection plates (i.e. bracket plates) |
Conclusion
Linear buckling analysis should be performed if buckling of plates is a possibility in the connection. According to AISC 360-16 – J.4, stability of plates in connections is ensured if slenderness λ ≤ 25, which corresponds to buckling factor αcr = 13 for 36 ksi yield strenght plates and αcr = 9.16 for 50 ksi for LRFD. If buckling factor is over 13 no further buckling checks are necessary and plastic analysis may be used without reservations.
For plates connecting individual members, e.g. gusset plates with only one side restrained, the global buckling limit factors from AISC 360-16 – J.4, αcr ≥ 13, should be used. For stiffening plates in the joint, e.g. stiffeners, ribs, short haunches, and gusset plate with two or more sides restrained, the local limit buckling factor may be considered αcr ≥ 3.
It is still possible to design a joint with a smaller buckling factor, but buckling checks must be performed by hand or by geometrically nonlinear analysis with imperfections.
In the Catalog of AISC limit states - Compressive yielding and buckling entry, Prof. Denavit summarizes the use of IDEA StatiCa linear buckling calculation to assess the buckling limit state in steel connections.
References
AISC. (2016). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
Dowswell, B. (2006), Effective Length Factors for Gusset Plate Buckling, Engineering Journal, AISC, Vol. 43, No. 2, pp. 91–101.
