Shear in RCS - circular cross-sections
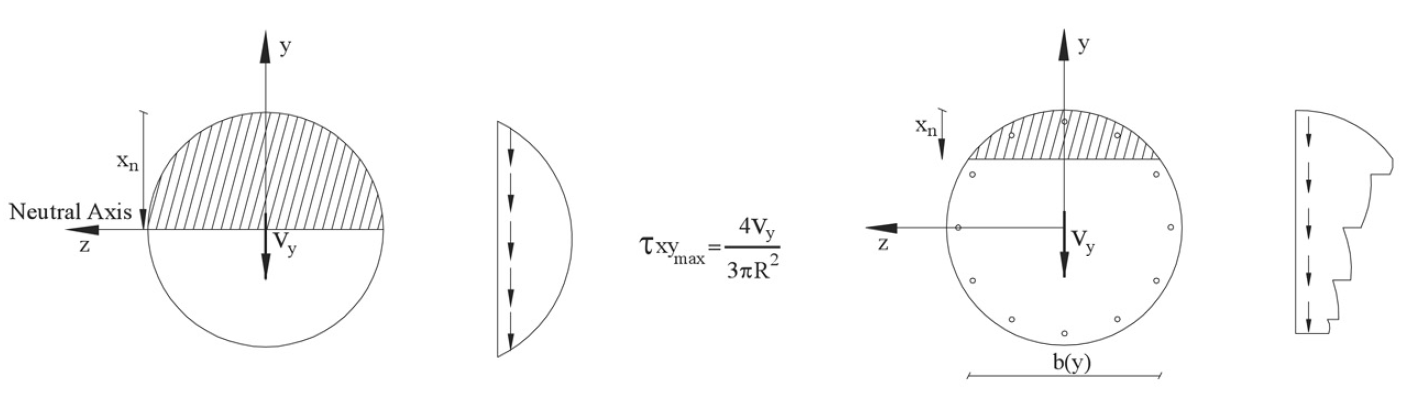
To begin with, let us recall the directions of shear stress in a circular cross-section.
Shear stresses for an uncracked solid circular cross-section have a vertical direction and are assumed to be constant through the width b. If flexural cracking occurs in the section the vertical shear stress distribution will be modified. A sketch of such shear stress distributions can be found in the following figure.
For determining shear stresses on closed thin-walled members, it is assumed that the shear stresses are uniformly distributed over the entire thickness t of the wall and act parallel to the section boundaries.
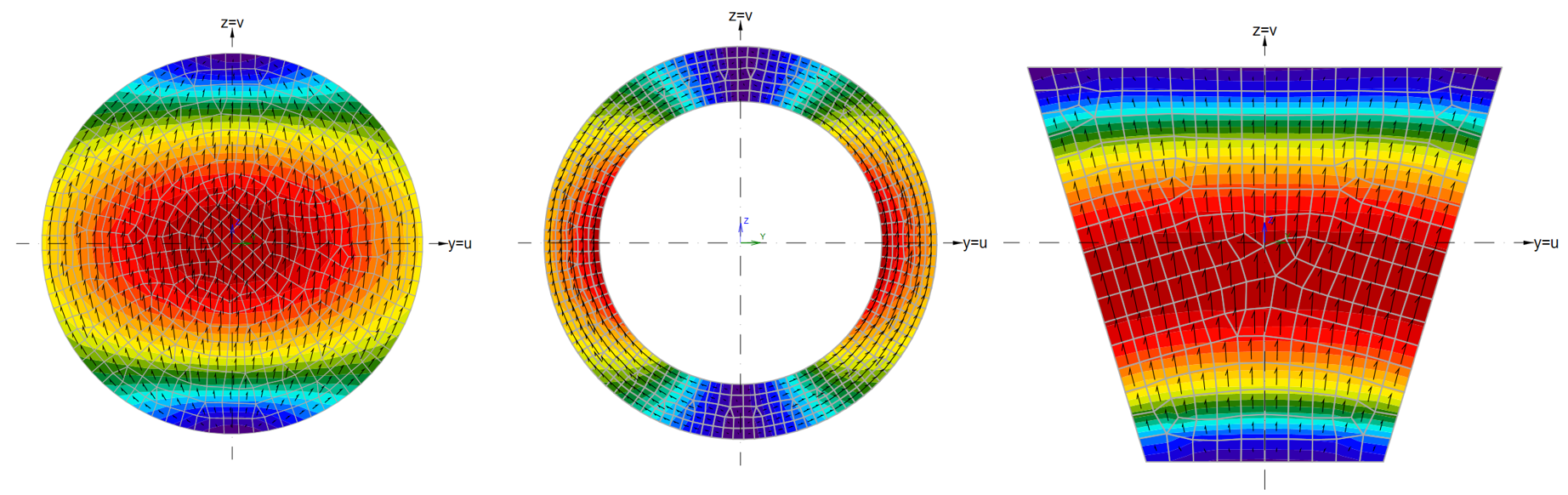
These assumptions can be verified by FEA analysis of the cross-sections. In the following figure, we can see the results of the FEA analysis for three types of cross-section - solid circular section, hollowed circular section, and trapezoidal section. The calculations were done in the General cross-section editor tool. Shear stresses caused by unit shear force Vv are displayed including arrows of the flow of stress.
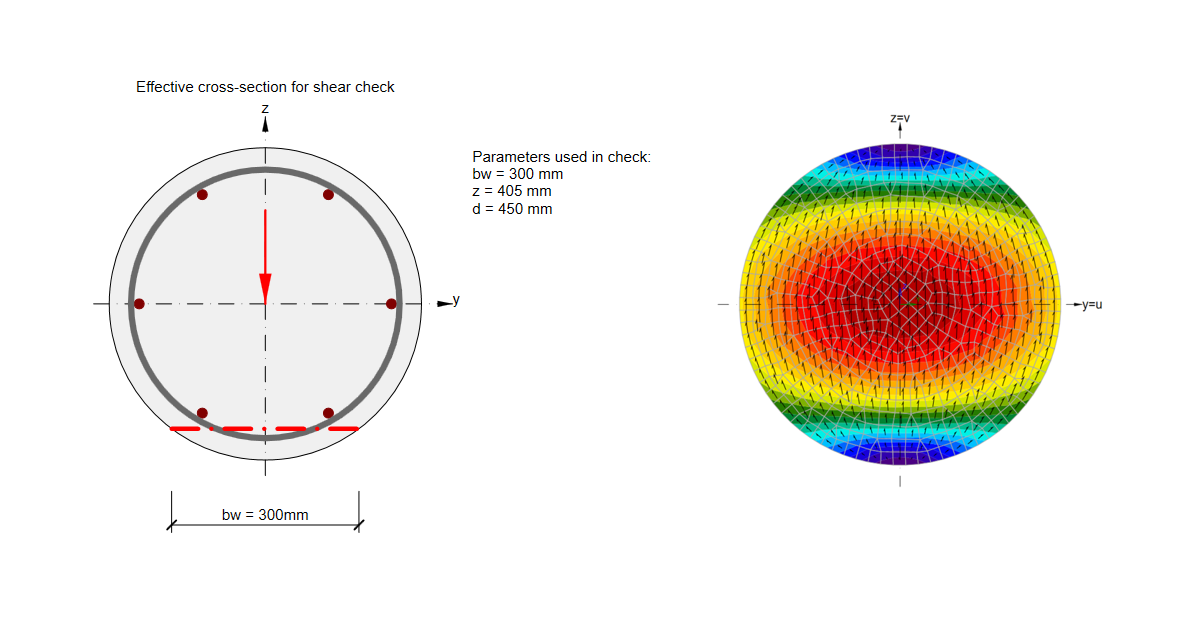
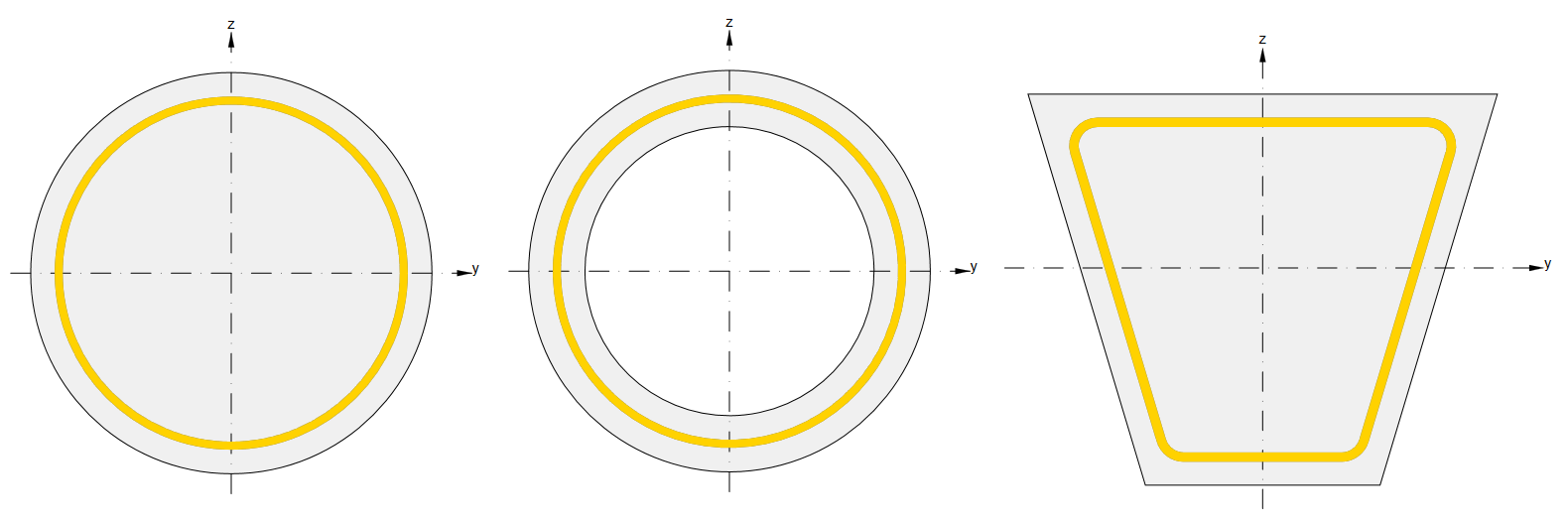
Let's consider stirrups equidistant to the cross-sectional edges, as shown in the figure below.
We can notice that the shear stress flow in the solid circular section does not follow the stirrup geometry causing reduced effectivity of shear reinforcement. This effect is taken into account by the reduction factor χ, which influences the shear resistance VRd,s.
In IDEA StatiCa RCS, the reduction factor is calculated according to the following formula.
\[{χ}={{b}_{w}} / {{d}_{h}}\le 0.85\]
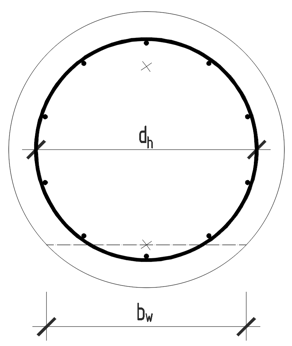
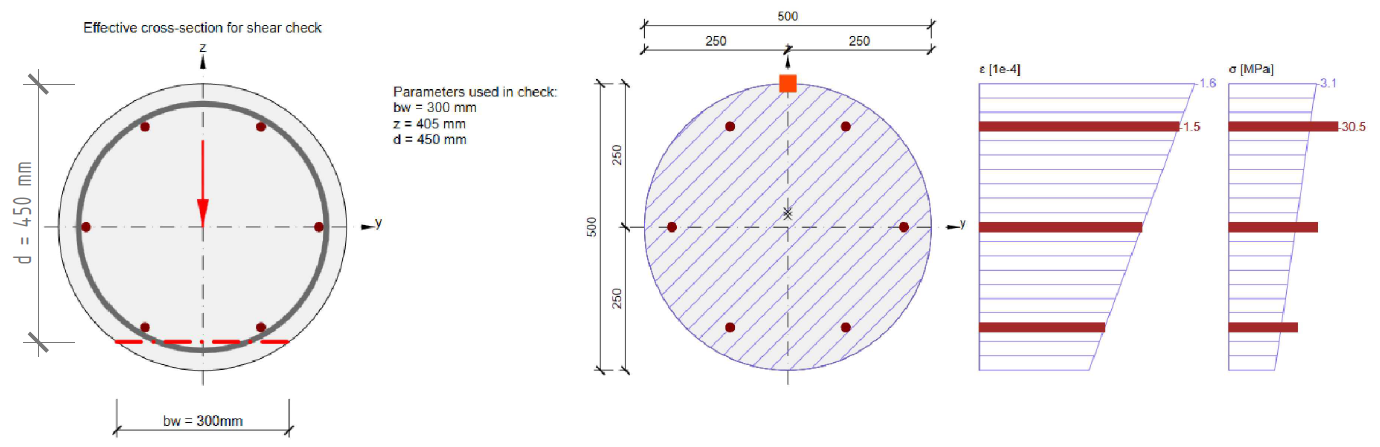
Where the bw is the shear width and dh is the diameter of the circular stirrup.
The shear width bw is calculated in several ways.
1. Method
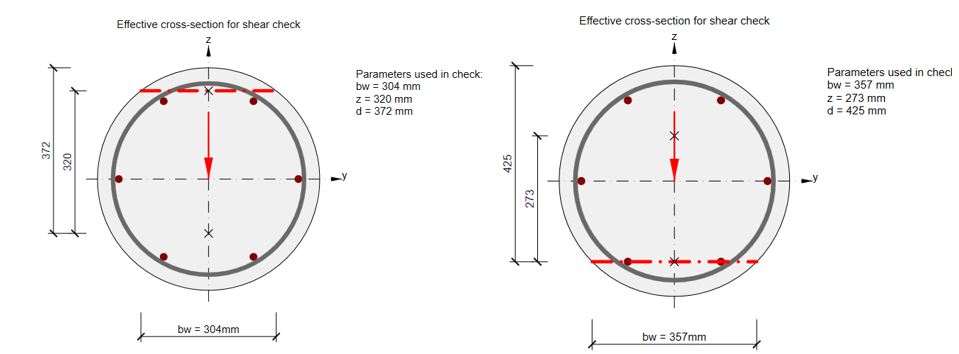
The shear width bw is calculated as the minimum width between tension and compression chords in case of the occurrence of flexural cracks in ULS. It can be seen in two examples of a circular section in the following figure.
2. Method
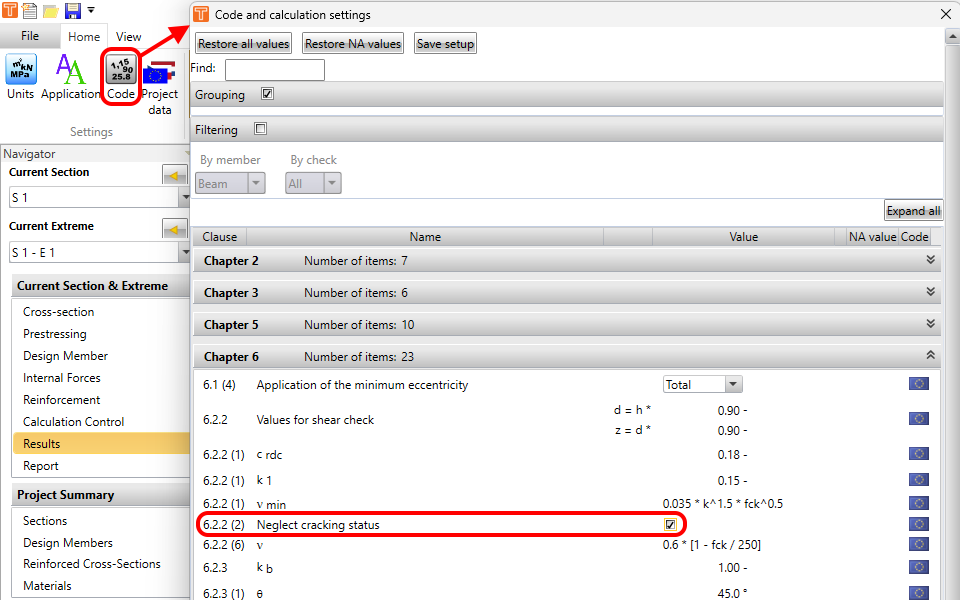
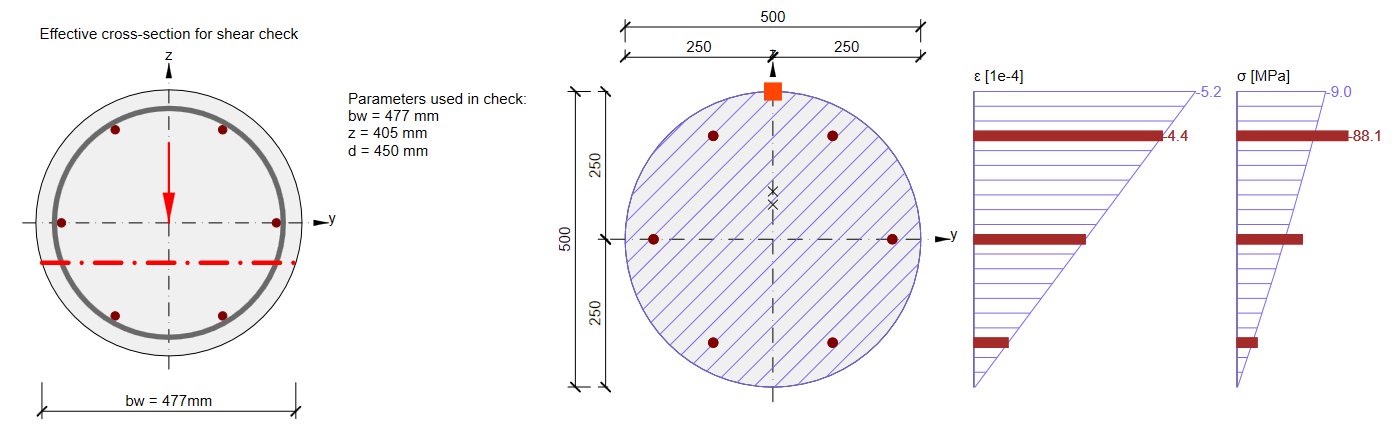
If the status without flexural cracks is neglected - see the figure:
And if there is no tension or compression chord in the cross-section (the whole section is under the compression or tension), bw is the width of the cross-section at distance d from the edge of the cross-section. Where d is the effective depth and is calculated as d=0.9*h for sections without tension or compression chord (fully compressed or fully tensioned).
3. Method
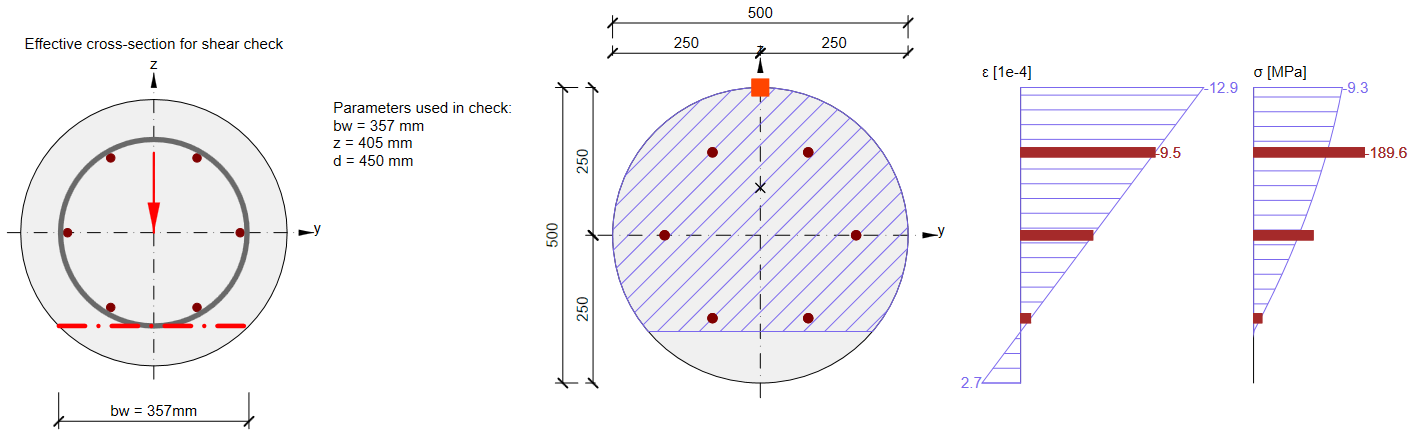
If the status without flexural cracks is considered (according to EN 1992-1-1 6.2.2(2)) and the cross-section is not affected by flexural cracks in ULS. The value of bw is calculated at the level of the maximal principal tension stress.
4. Method
A cross-section that is affected by flexural cracks but only the compression chord or only the tension chord exists - the area for which the program looking for the smallest value of bw is bounded on one side by the existing centre of gravity of the concrete in compression (or the centre of gravity of the reinforcement in tension), the other side of the area is defined by the shear reinforcement.
5. Method
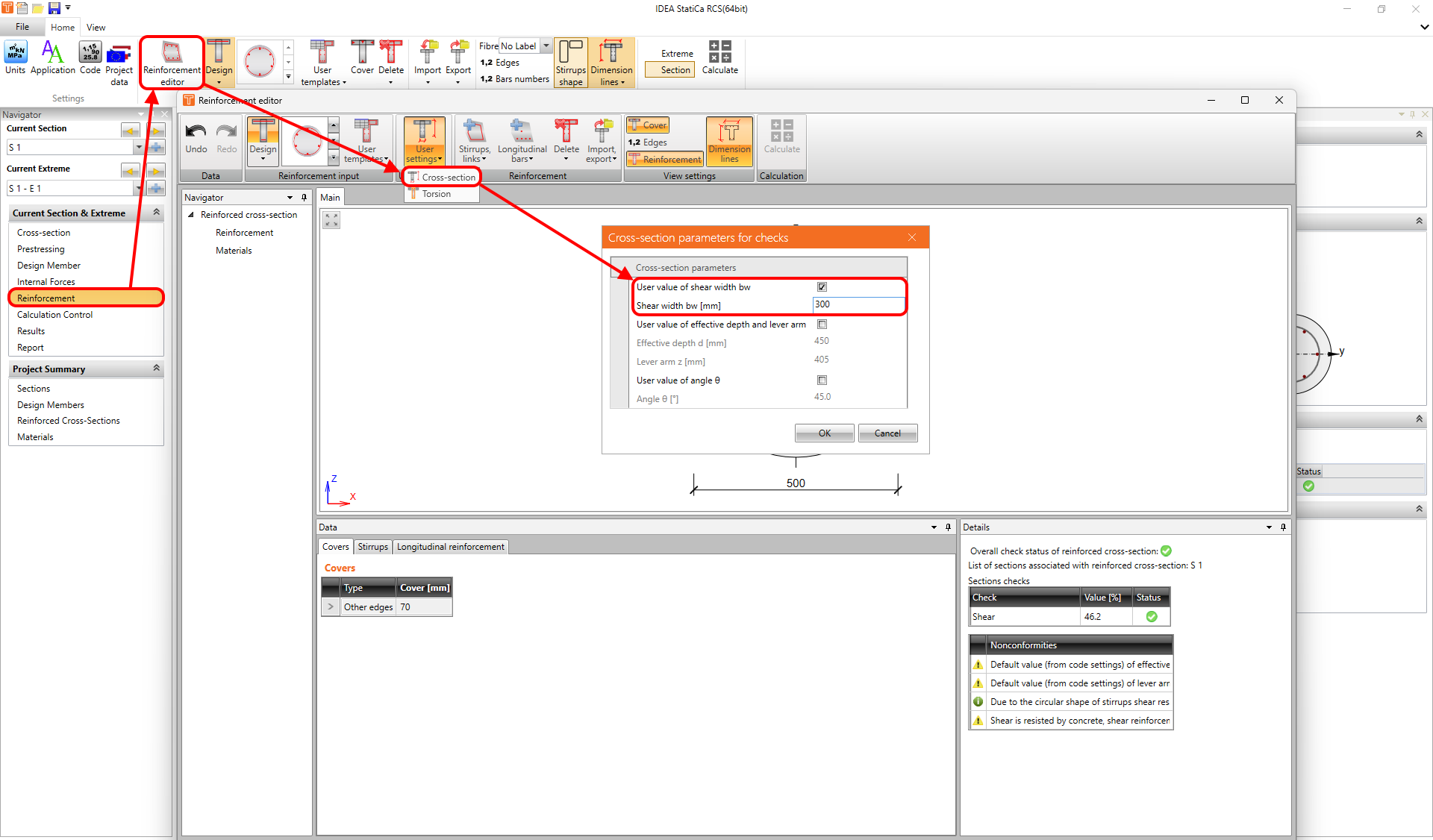
In some cases, it is worth considering setting the value of bw manually. It can be done in the Reinforcement editor.