Prestressing in Detail - Post-tensioned tendons

Introduction and assumptions

First, let's start with a brief description of our concrete design software. This article is mainly about prestressed concrete design in the Detail application which is generally developed for discontinuity regions design or for the design of members containing discontinuity regions such as openings, dapped ends etc.

For comparison of results, we will use the Beam application whose purpose, as you can guess from the name, is concrete beam design. 

Secondly, we need to define a  few assumptions and restrictions to understand the design of prestressed concrete beams in Detail better. 

• The Time Depended Analysis (TDA) is not implemented in the Detail application. On the other hand, TDA is implemented in the Beam app. for the design of prestressed concrete beams.
• TDA can be simulated in Detail using the creep coefficient and the increments. 
• Shrinkage and temperature loads are not implemented in the Detail
• The concrete in tension in the Detail is excluded. So for our comparison, we need to have the beam without cracks. Of course, the same approach can be used generally for beams affected by cracks, but the results will not be then the same in the Beam because only linear calculation is provided in the Beam.

Increments

Before we go through the example, we need to understand how the increments work for prestressed concrete design in the Detail. 

There are 3 load types that are applied to the model in three increments in the Detail app.

• Prestressing - for increment P
• Permanent - for increment G
• Variable - for increment V

If you create a combination containing load cases of all load types, the whole portion of Prestressing load type will be applied in the first increment P, the whole portion of Permanent load type will be applied in the second increment G, and the whole portion of Variable load type will be applied in the third increment V.

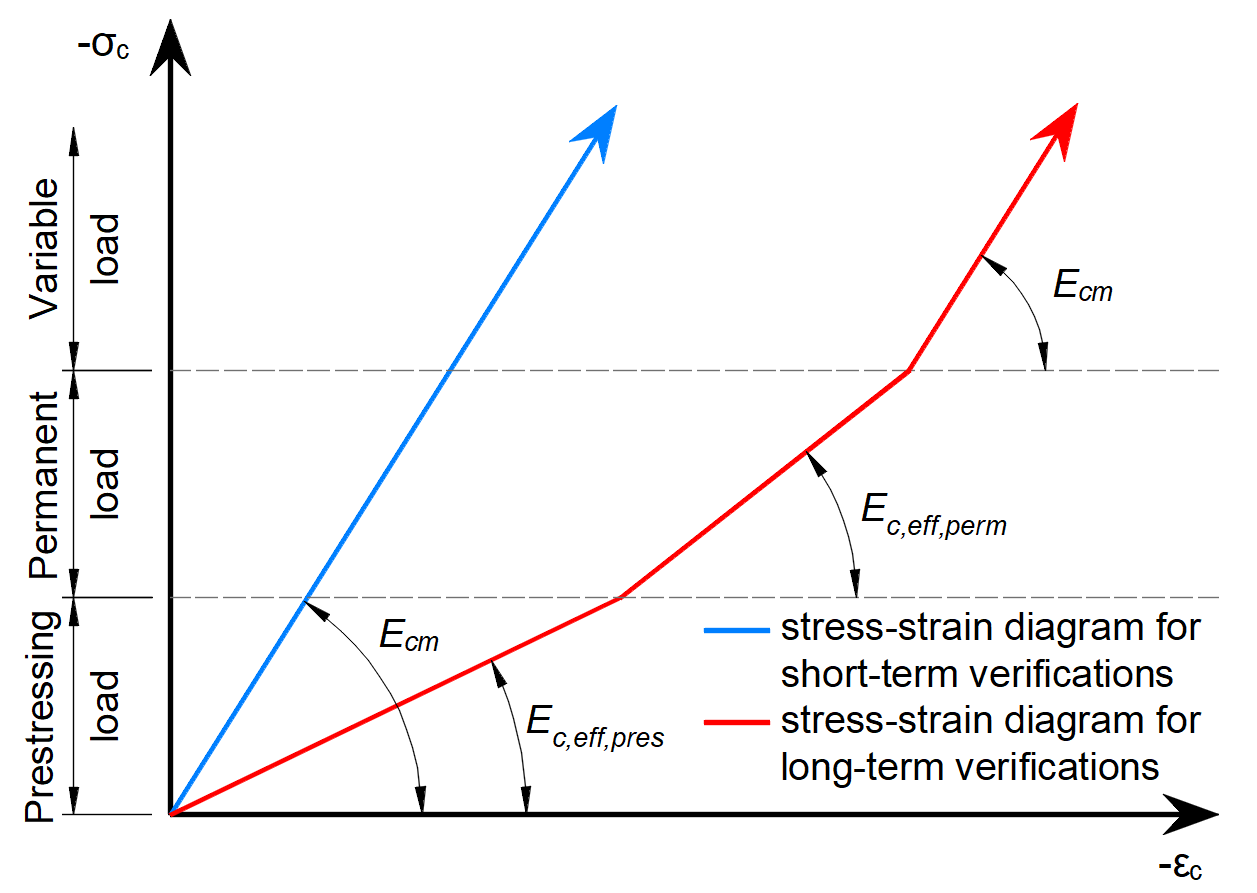
The reason why there are increments is that the different material models (different modules of elasticity) are used for SLS calculations (for ULS there is only one material model defined in Material model (EN)).

As you can see there are three modules of elasticity:

• E_c,eff,press = E_cm / (1+φ_press) - Effective modulus of elasticity of concrete for P increment
• E_c,eff,perm = E_cm / (1+φ_perm) - Effective modulus of elasticity of concrete for G increment
• E_cm - Secant modulus of elasticity of concrete

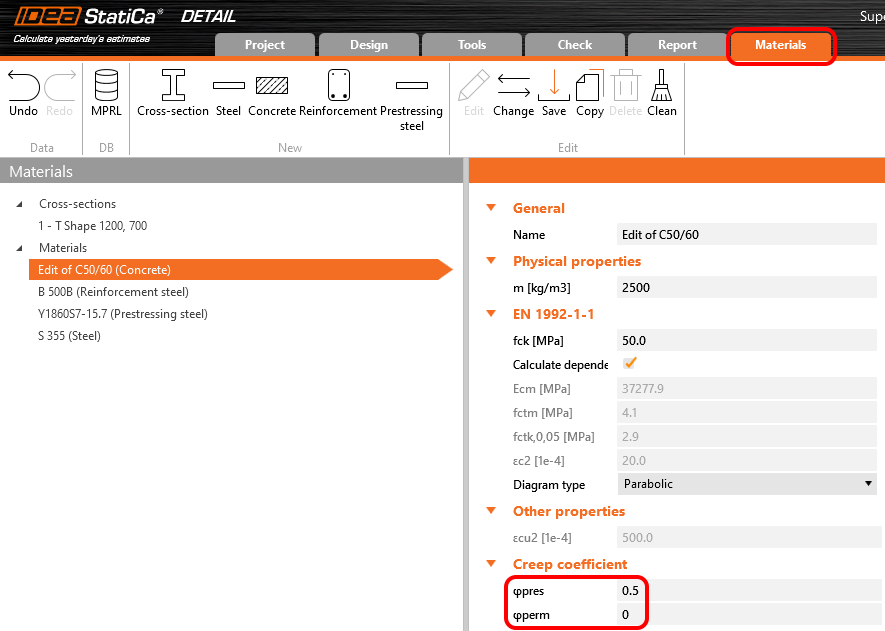
Where the φ_press and φ_perm are the creep coefficients for the P and G increments. The coefficients can be set in Materials & models.

Please note that for short-term effects only E_cm is used. It is valid for all three increments. And the long-term loss is taken into account only for long-term effects.

The beam parameters

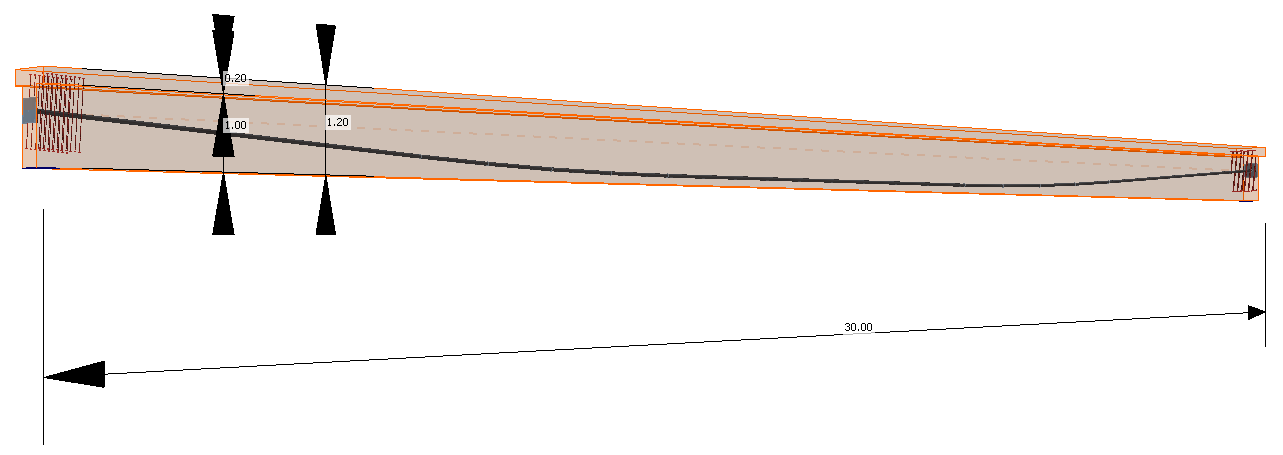
Two identical models are created in the Beam and Detail applications. They are attached at the end of this article. Download them and go through them while reading the article. 

The example of a concrete beam will be introduced in the Beam application and then the comparison with the Detail application will be done for three construction stages.

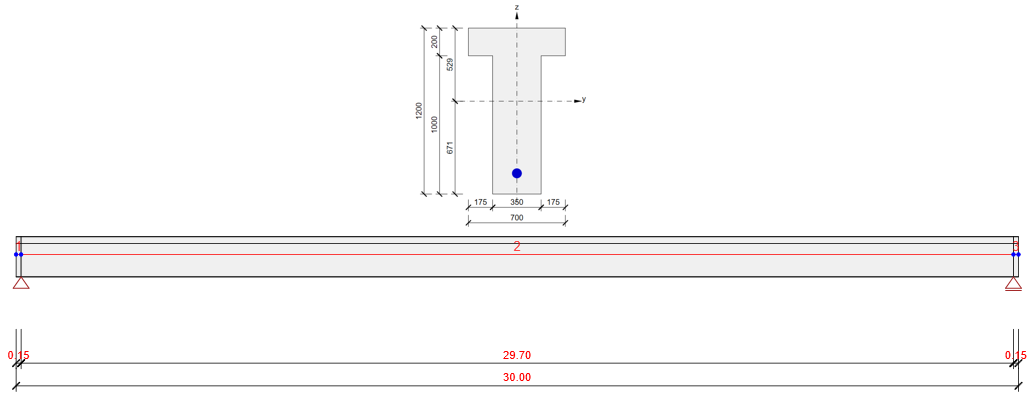
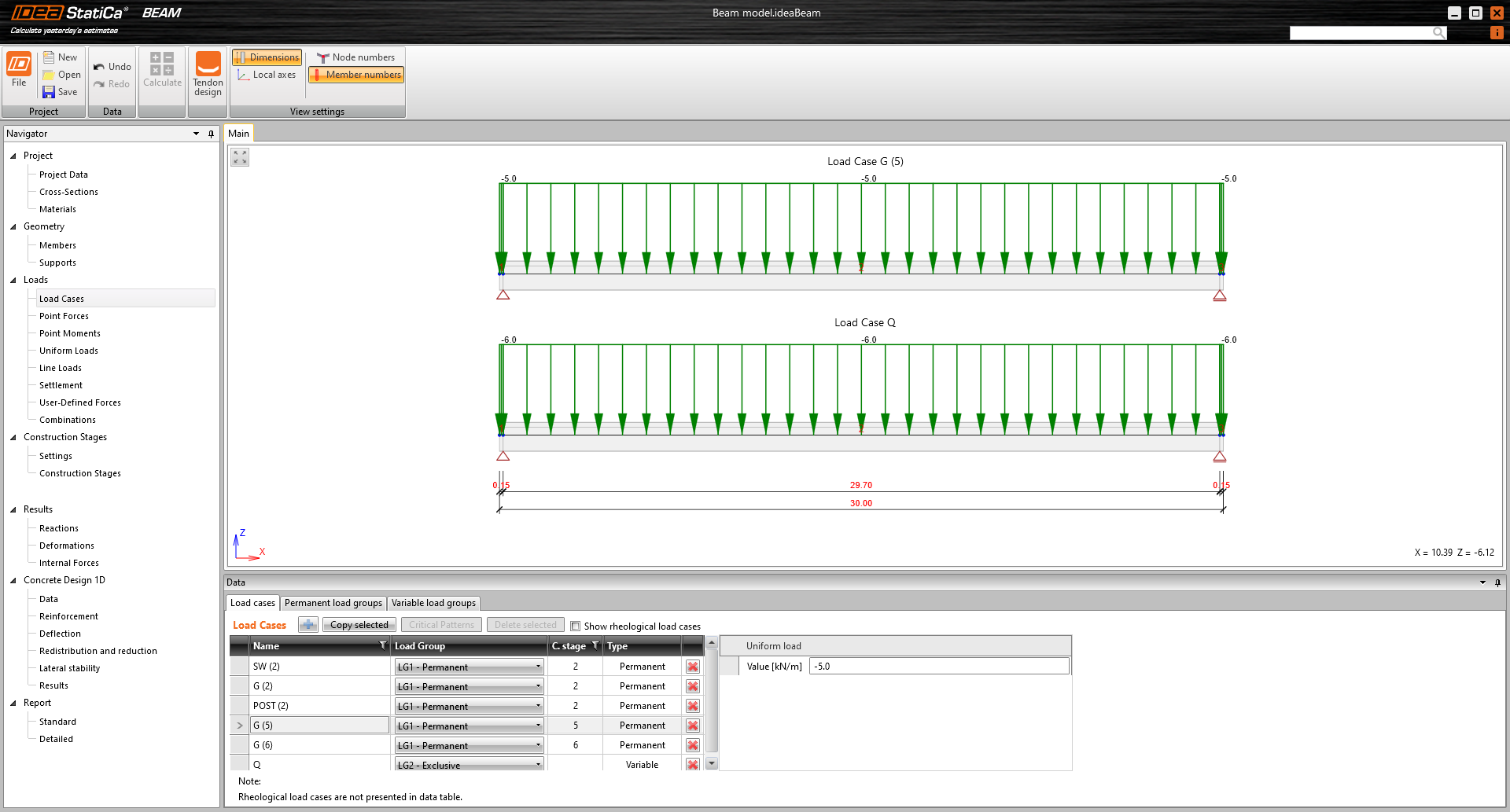
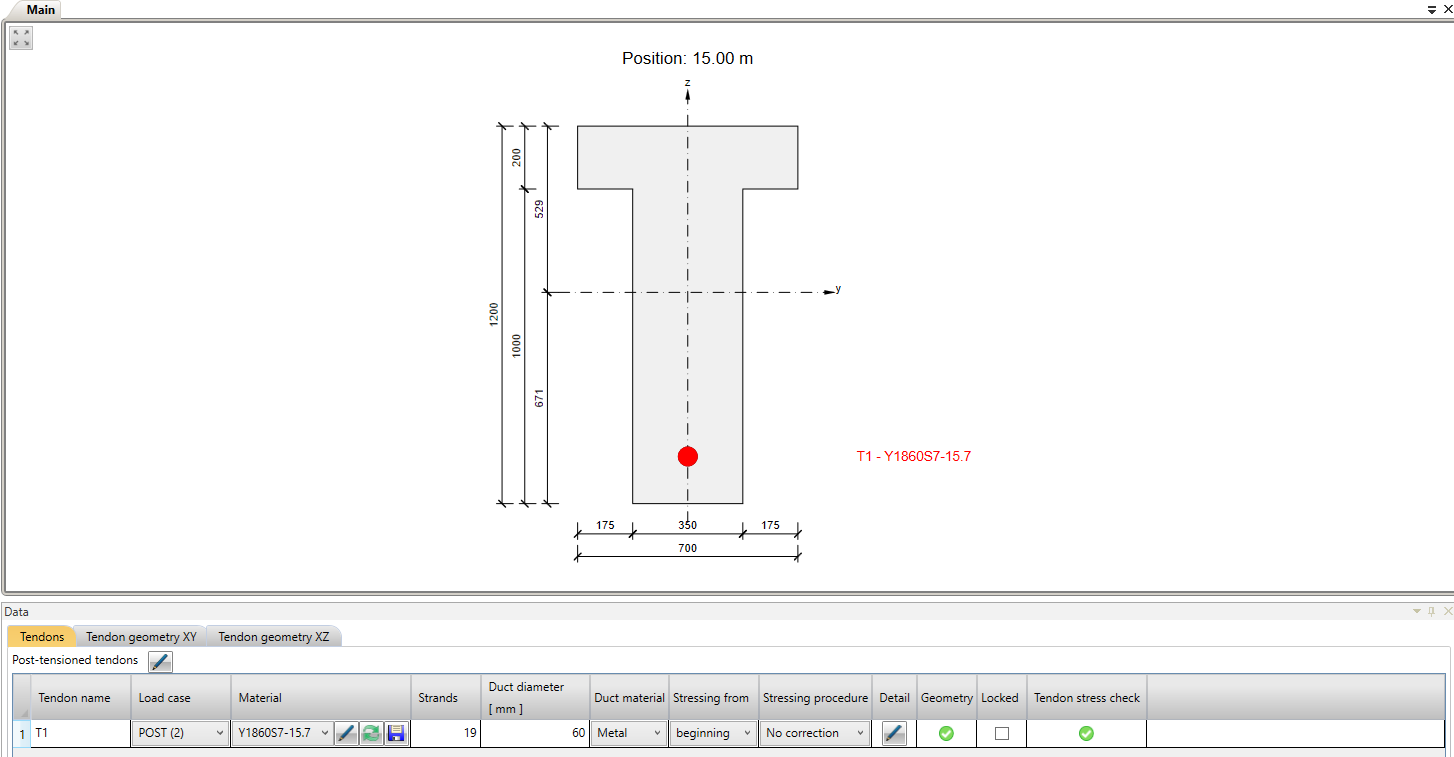
The example is a single span simple beam of T cross-section made of C50/60 concrete prestressed by a post-tensioned 19-strand tendon.

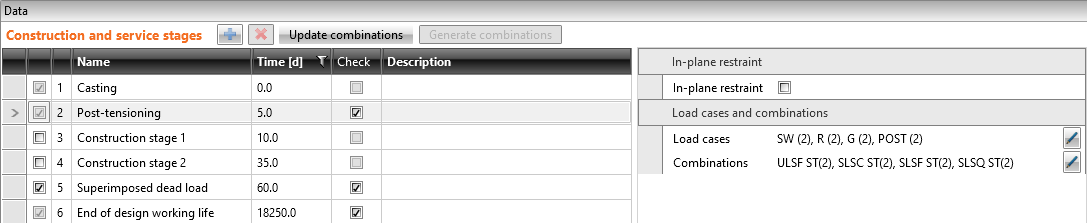
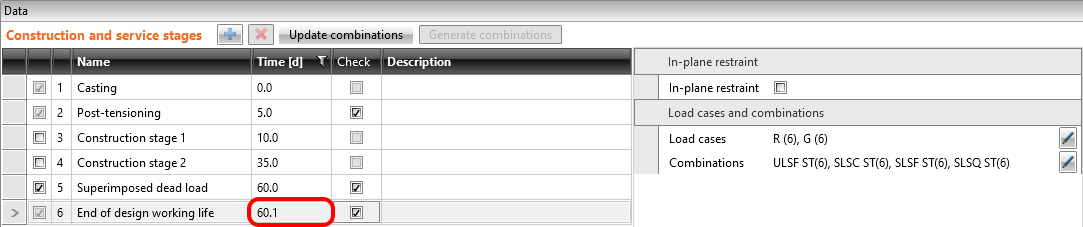
We will check the beam in three construction stages.

1. Transfer of prestressing - 5 d (just after application of prestressing)
2. Superimposed dead load - 60 d (start of working life)
3. End of design working life - 18250 d (50 years)

The other stages can be carried out similarly.

There are only four load cases input. The numbers in the brackets are the numbers of the construction stages where the individual loads are applied.

1. Self-weight - SW (2)
2. Prestressing - POST (2)
3. Permanent load - G (5)
4. Variable load - Q

Other load cases are empty.

Now let's take a look at the prestressing. There is one 19-strand tendon. Note the diameter of the duct. The Beam application takes into account the weakened cross-section by the duct. On the other hand, the Detail application takes into account the full section. So to get the best possible match of results the duct diameter was set with the smallest possible diameter in the Beam application.

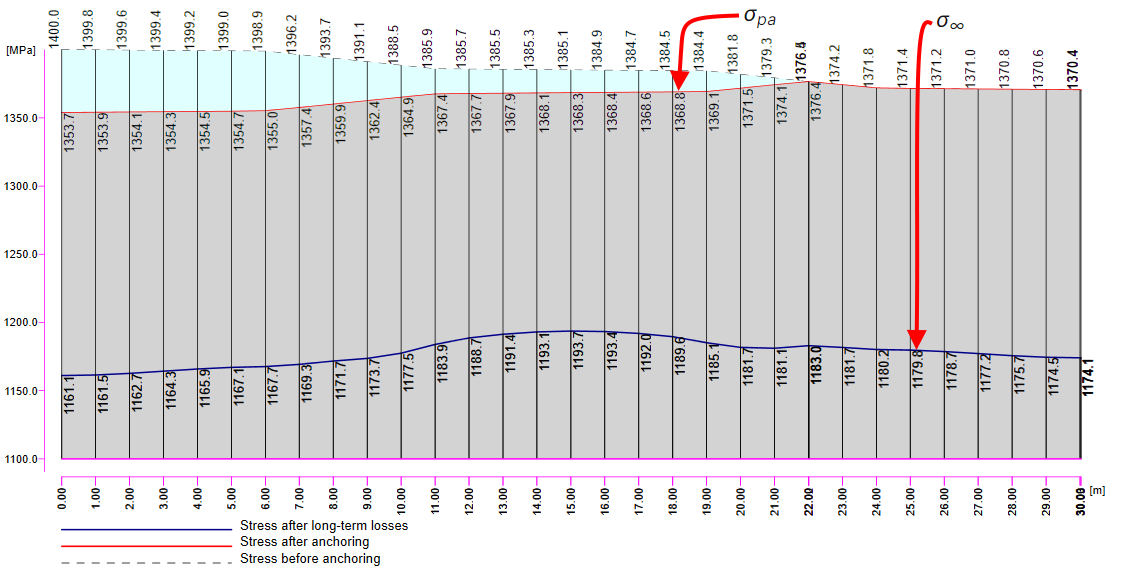
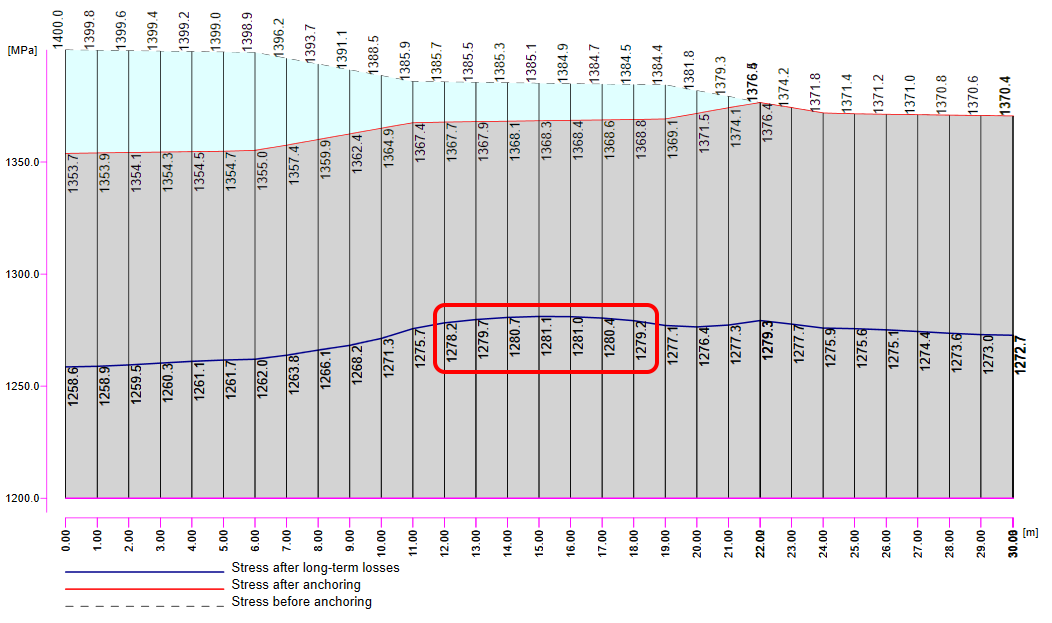
In the next figure, you can see the Tendon Stress/Losses chart. 

There are several values of stress in the tendon that should be controlled during the prestressing application. At this point, we will stop and briefly explain the prestressing process and individual stresses and losses.

Prestressing process for post-tensioned beam

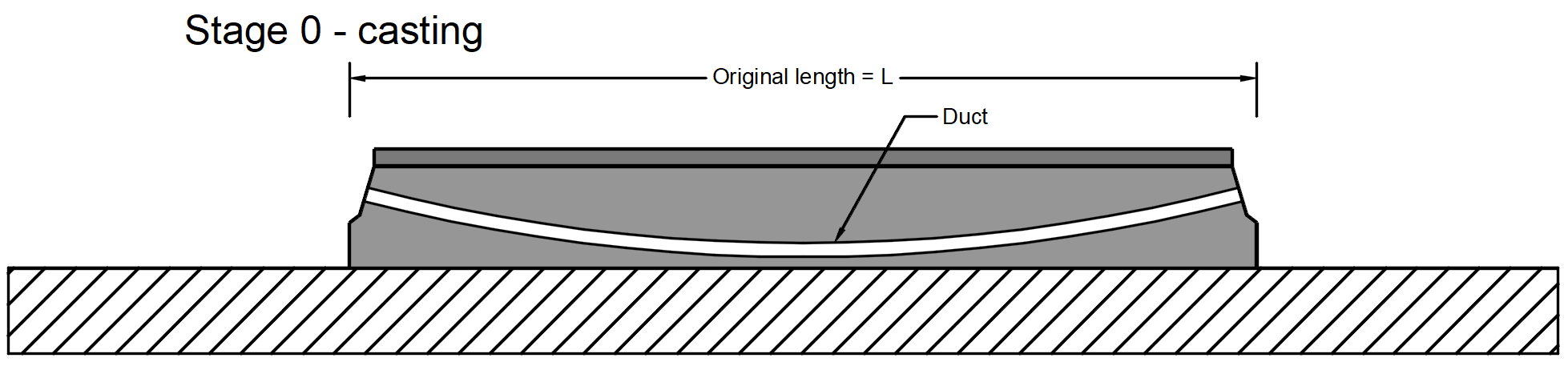
Stage 0 - casting -> The concrete member is cast containing reinforcement and an empty duct.

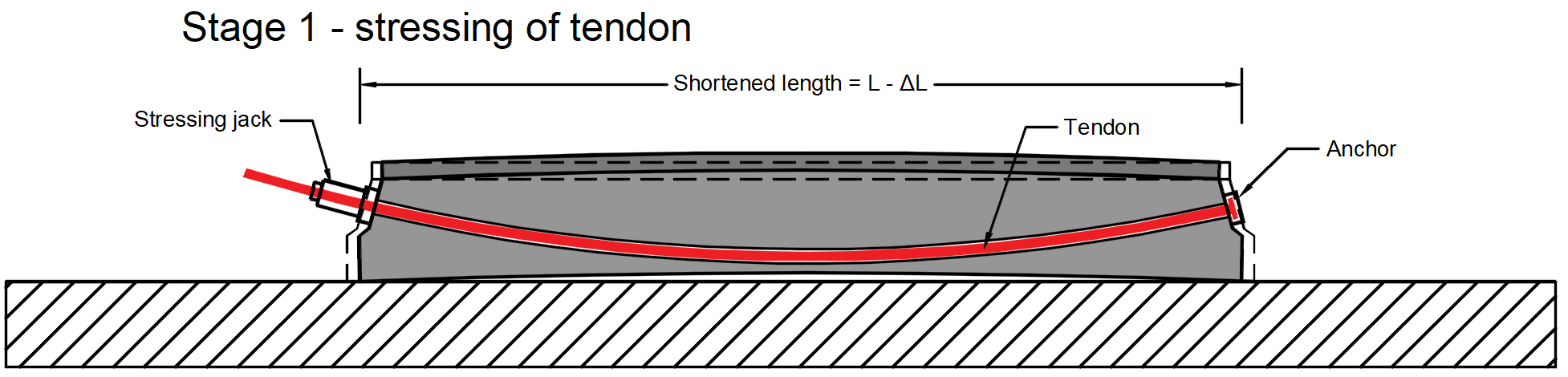
Stage 1 - stressing of tendon -> The tendon is inserted into the duct, anchored on one side and prestressed by stressing jack on the other side (or it can be stressed in two steps from both sides, but it is not our case). During the stressing process, the beam deforms. So there is initial stress σ_p,ini at the stressing jack, stress before anchoring in the tendon which is an initial stress affected by the frictional loss Δσ_pμ. In our example σ_p,ini = 1400 MPa.

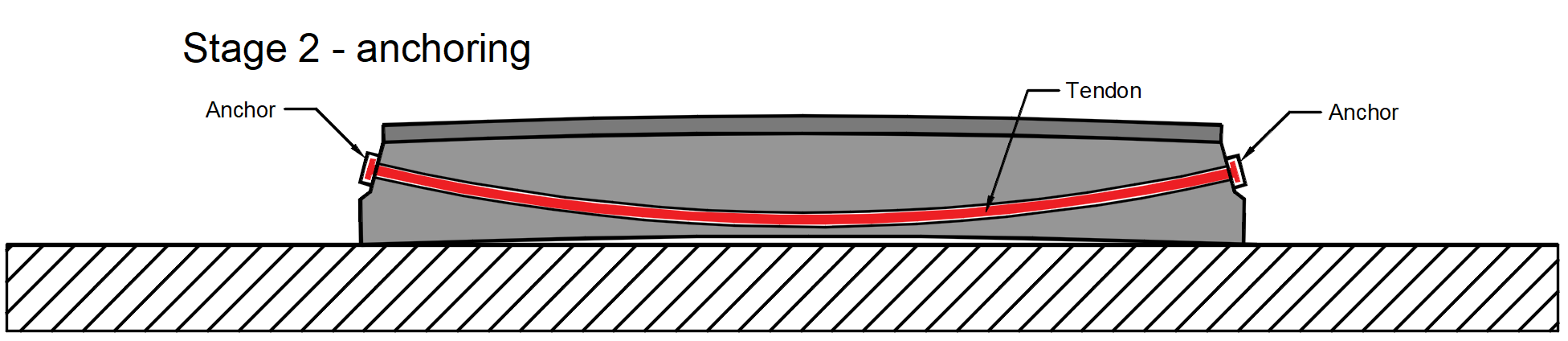
Stage 2 - anchoring -> The stressed end is anchored and the anchorage set loss (slip) Δσ_pw happens. There is no other loss due to the immediate elastic concrete strain because the immediate elastic concrete strain was realized before anchoring. The stress after anchoring (after short-term losses) σ_pa will be in the tendon at the end of this stage.

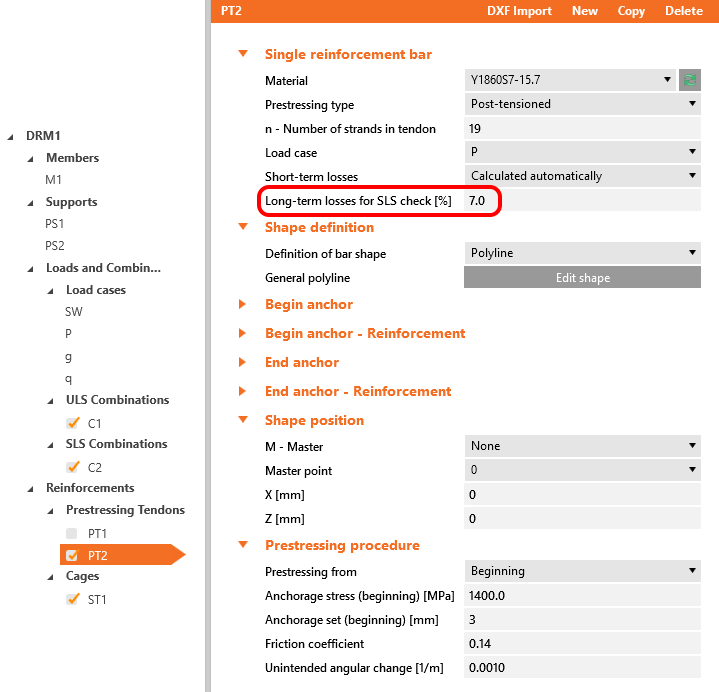
In the case of post-tensioned tendons, you can input the prestressing effect in Detail in two ways. 

• Short-term losses are calculated automatically - The input is the Anchorage stress (initial stress) σ_p,ini. The losses Δσ_pμ and Δσ_pw are calculated automatically based on the Anchorage set, the Friction coefficient, and the Unintended angular change which are also inputs in this case.
• Short-term losses are defined by the user - The input is the stress after anchoring (after short-term losses) σ_pa. You input the value of the stress in each vertex of the tendon.

Note that in Detail the automatic calculation of short-term losses doesn't include the correction of relaxation. It was also turned off on the Beam in our example.

• Read more: Prestressing in Detail - Model description

Transfer of prestressing stage

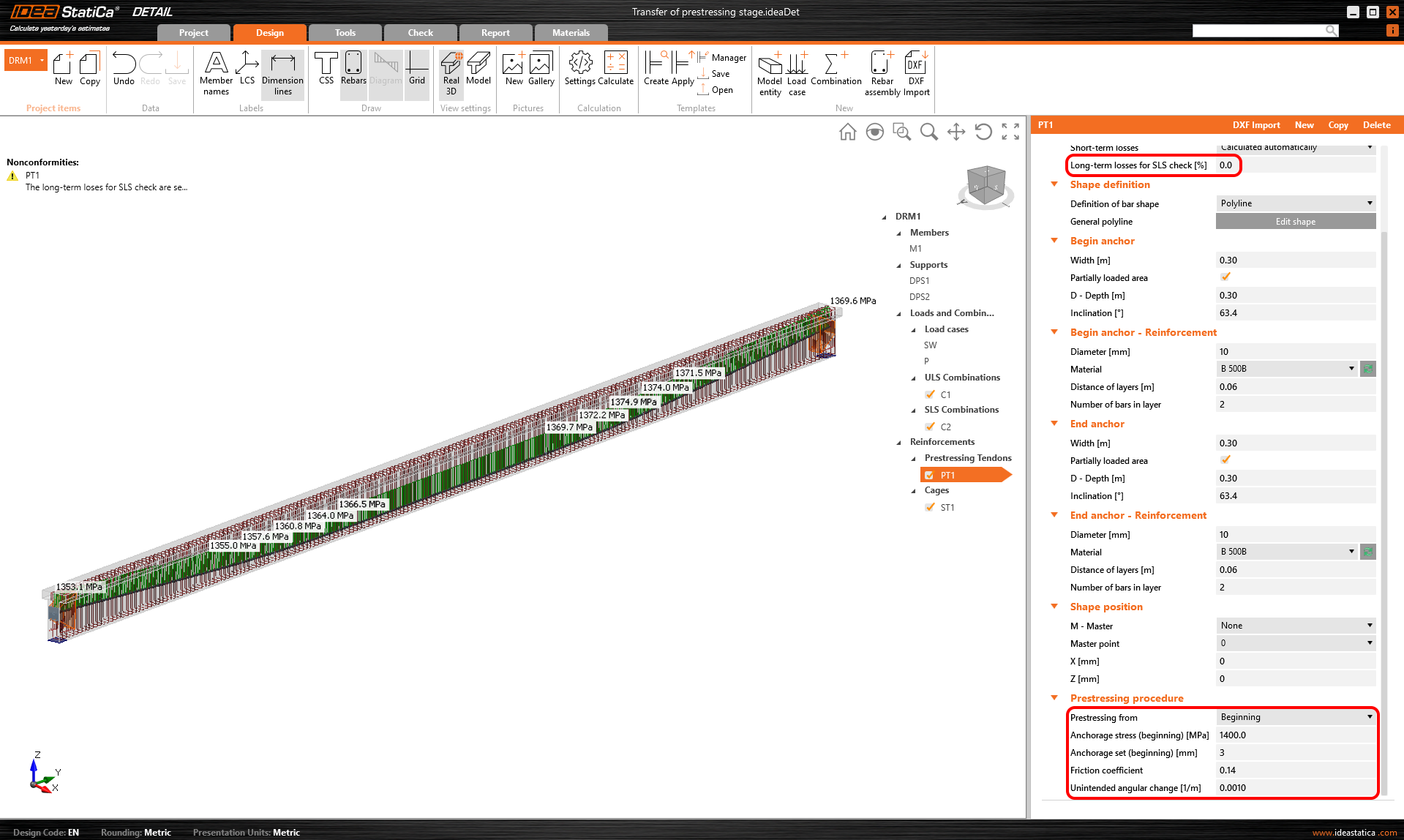
The model is defined so let's switch to the Detail application and have a look at how to set the first stage. The model is the same we only added stirrups for shear transfer, but it will not influence the results.

For this stage, there are only two load cases:

1. SW - Prestressing type (Self-weight)
2. P - Prestressing type (Prestessing)

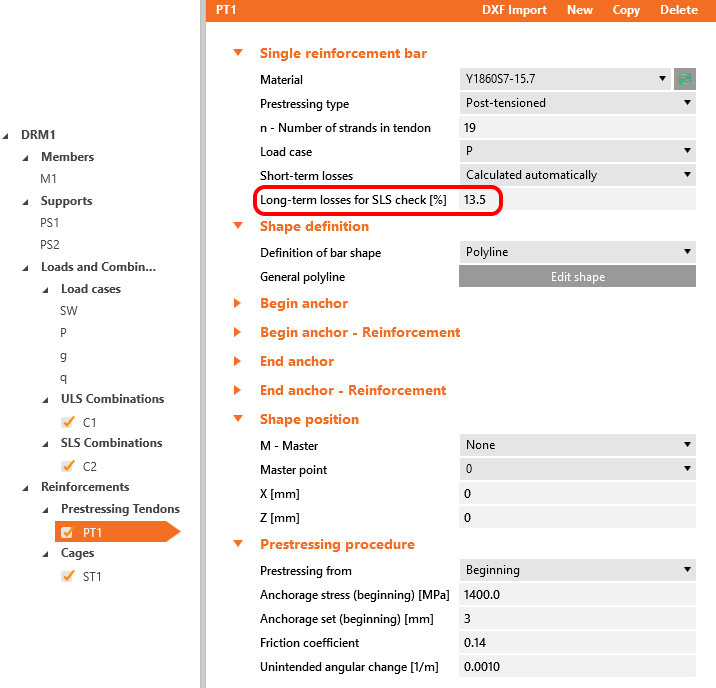
Both of them will be applied in the first load increment. Long-term losses for SLS checks are set to 0% and the values for the prestressing procedure are input the same as for the model in the Beam application. You can also compare automatically calculated stress after short-term losses σ_pa with the Tendon Stress/Losses chart from Beam.

• Read more: General description of Load impulses in Detail application

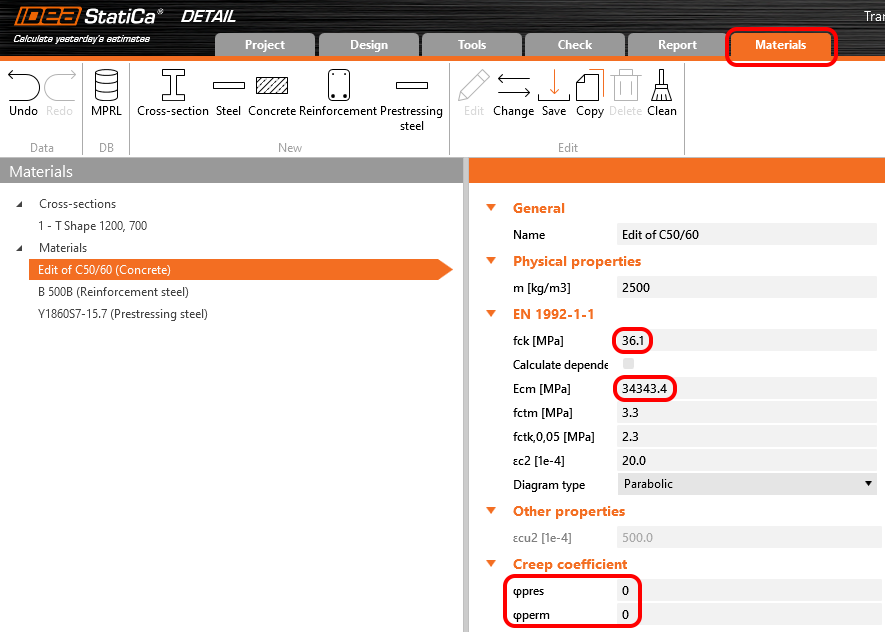
Creep coefficients are also set to zero value because we want to assess the stage just after the transfer of prestressing. And you can also notice that the value of E_cm and f_ck was rewritten to 5 days values we input into the Beam.

So let's compare the results. In that case, the long-term and short-term effects are the same. Because we didn't input any long-term loss.

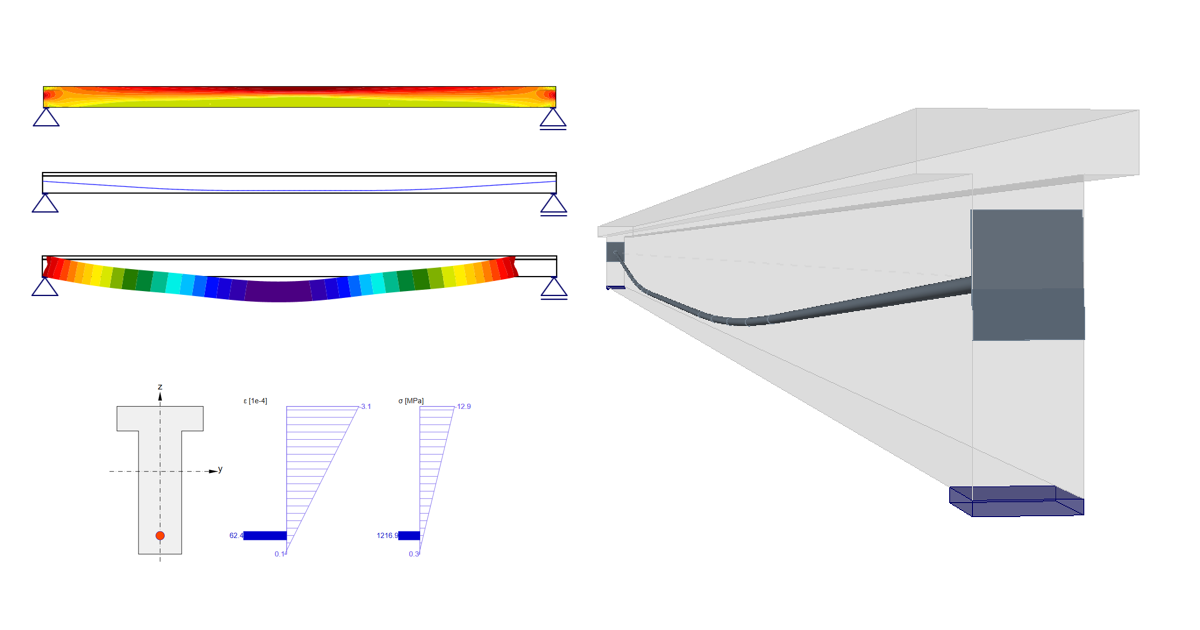
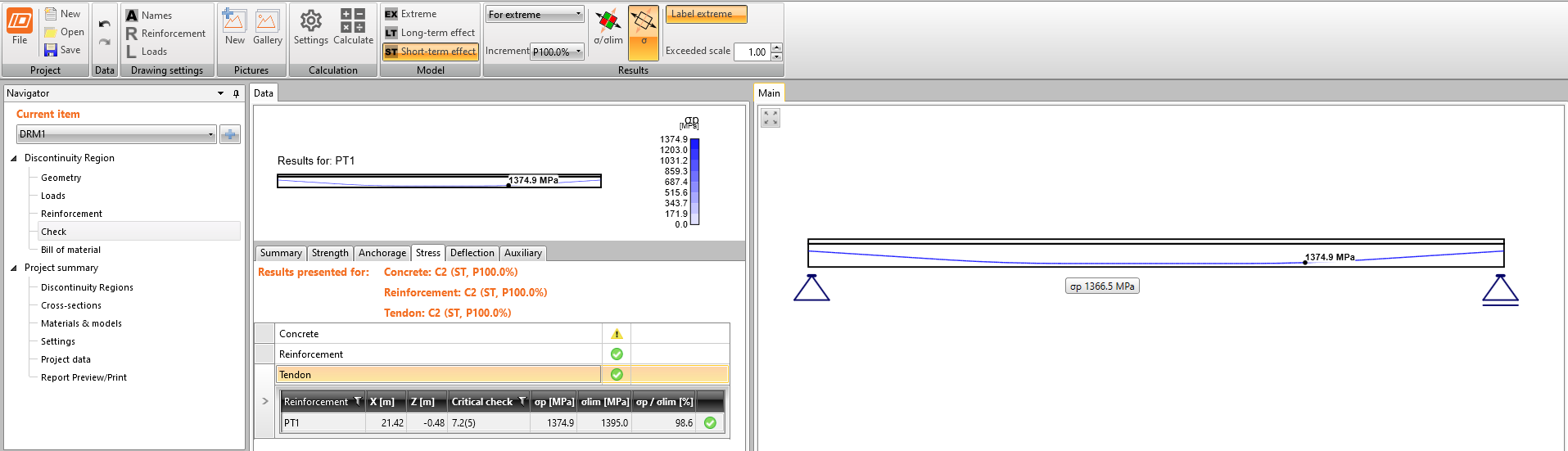
Stress in tendons in SLS - stress after short-term losses σ_pa:

Stress in concrete in SLS:

• Read more: General description of SLS results in Detail application

The SLS section check from Beam:

As you can see there is a good match. So it seems we have done the input for this stage correctly. Note that the coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) was set as 1.0 in Beam.

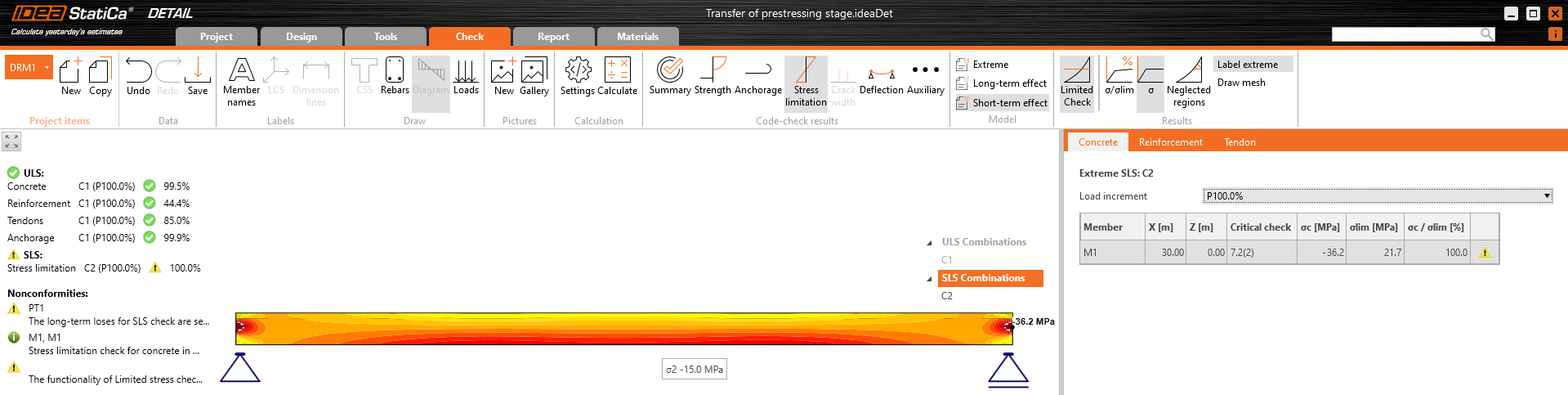
For ULS there will be greater difference. This is because of a different approach used in the Beam application to determine the response in ULS. In this case, the additional increment you can see in Beam results are unbalanced stresses. This is a completely different complex topic. The important thing is that the bearing capacity would be almost the same in the Detail and Beam applications.

• Read more: General description of ULS results in Detail application

Now you know how to use the Detail app for the design of prestressed concrete structures using post-tensioned tendons for the Transfer of prestressing stage. Just change the geometry and add some discontinuities like openings, etc.

Superimposed dead load stage

The time (age of the concrete) for this stage is 60 days. The purpose of this stage is to check the concrete beam at the start of its working life including permanent and variable loads. So the other two load cases are added. Load impulses are of course the same as in the Beam application model.

We need to determine two values as input for Detail. 

1. Creep coefficient for the time from 2 days to 60 days
2. Estimation of long-term losses for the time from 2 days to 60 days

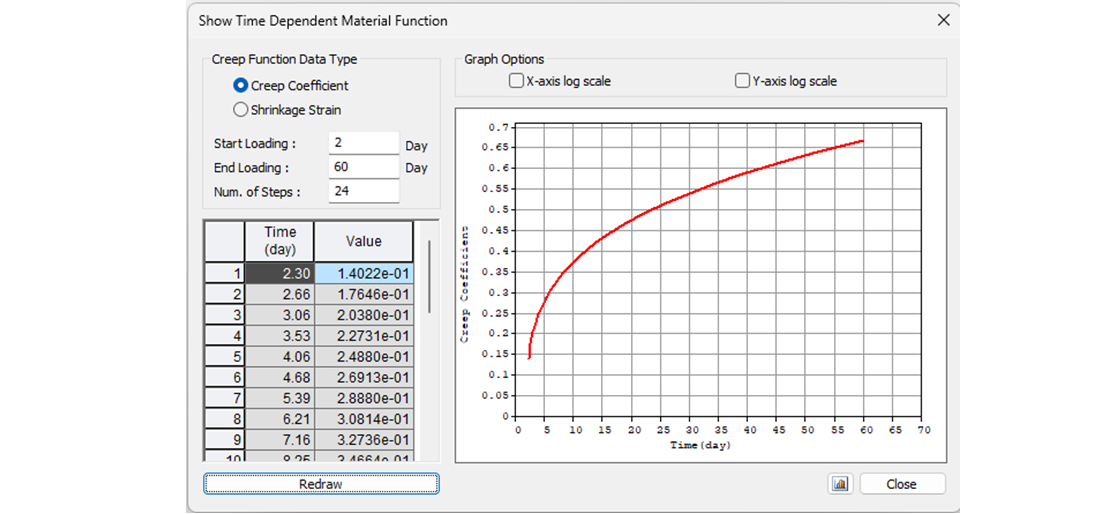
Let's start with the creep coefficient. In the following figure, you can see the creep function from 2 to 60 days for concrete grade C50/60 and cement class R according to the Eurocode. The value of the creep coefficient is then φ_pres ≈ φ₍₆₀₎ - φ₍₂₎ = 0.65 - 0.15 =  0.50

In Detail application, the creep coefficient can be set in Materials & models. It is obvious that the modulus of elasticity has to be set as the default E_cm value (recall the Increment chapter and the chart in it). You can also notice that the value of φ_perm = 0.0, which is because we want to apply permanent loads as short-time loads as well as variable loads.

Now it is time for the long-term losses. Of course, you can estimate them (my estimation would be 8%). It is the easiest way, but in our example, we want to do it precisely. So we calculated σ₆₀ - Stress after long-term losses in 60 days (blue line) in the Beam application by setting the final time to 60 days.

The value of σ₆₀ = 1280 MPa as can be seen in the following figure (blue line).

Then we need to look at the value of σ_pa again. We have already confirmed that the values are the same in Beam and Detail.

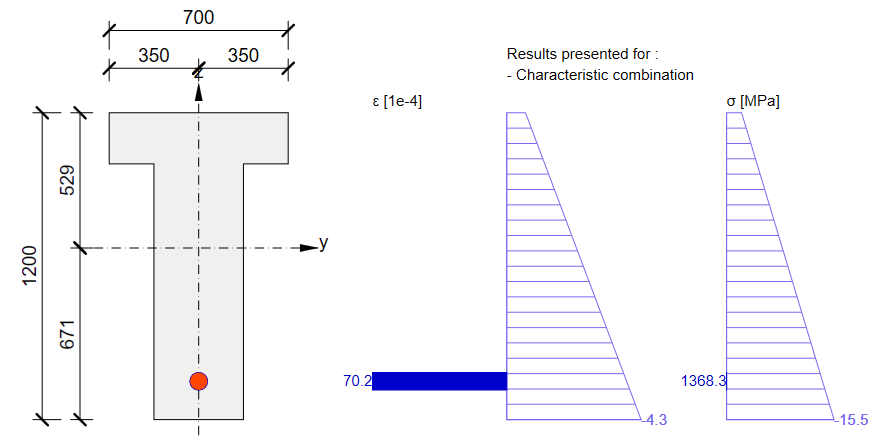
In the figure, we can see that σ_pa = 1368.6 MPa in the middle of the span.

The long-term losses can then be calculated as σ₆₀ / σ_pa = 1280 / 1368.6= 0.93 -> long-term loss is 7%. Let's input the value and compare the results.

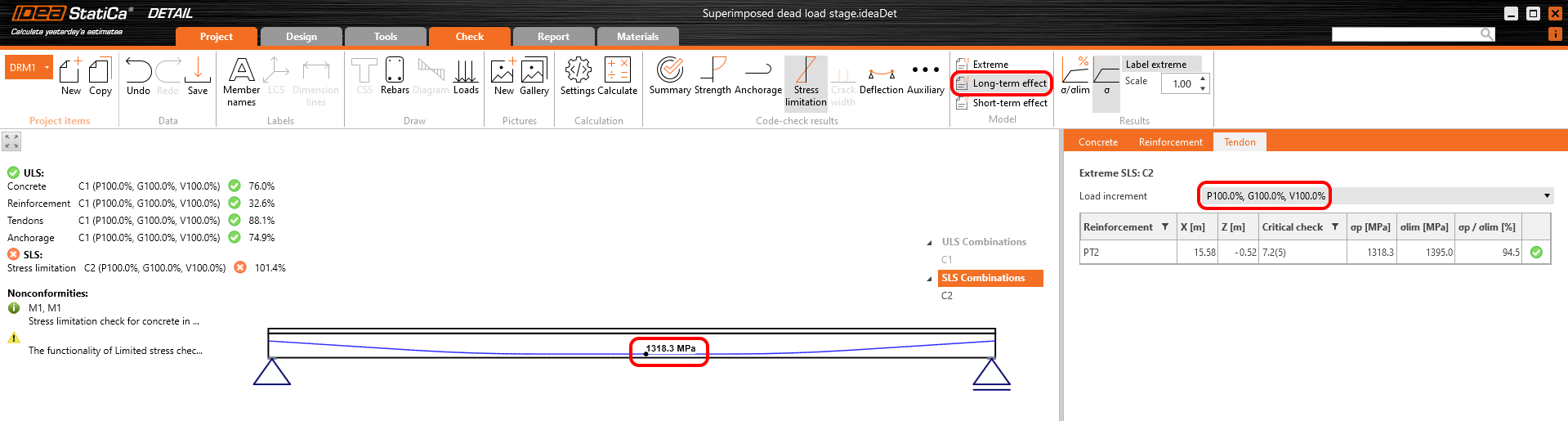
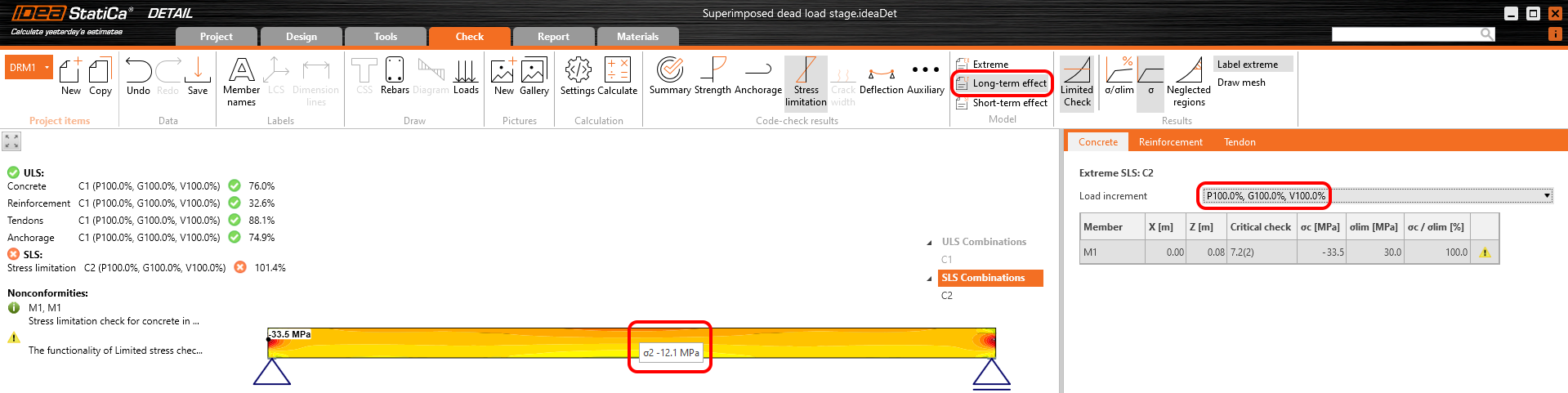
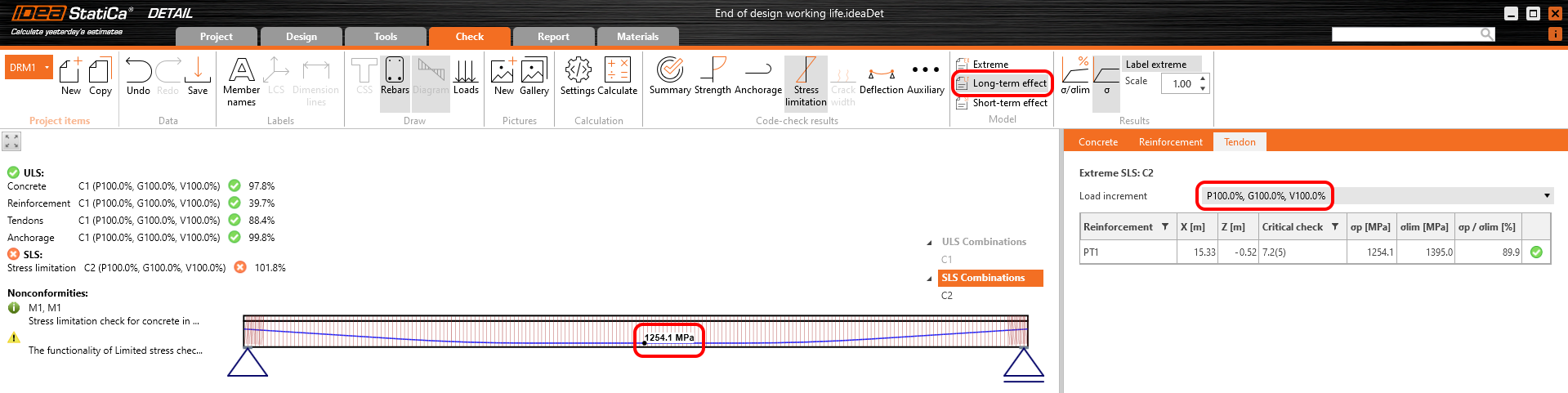
The results are read for long-term losses (we want to have creep and losses included) and for all increments (we want to have all loads included). 

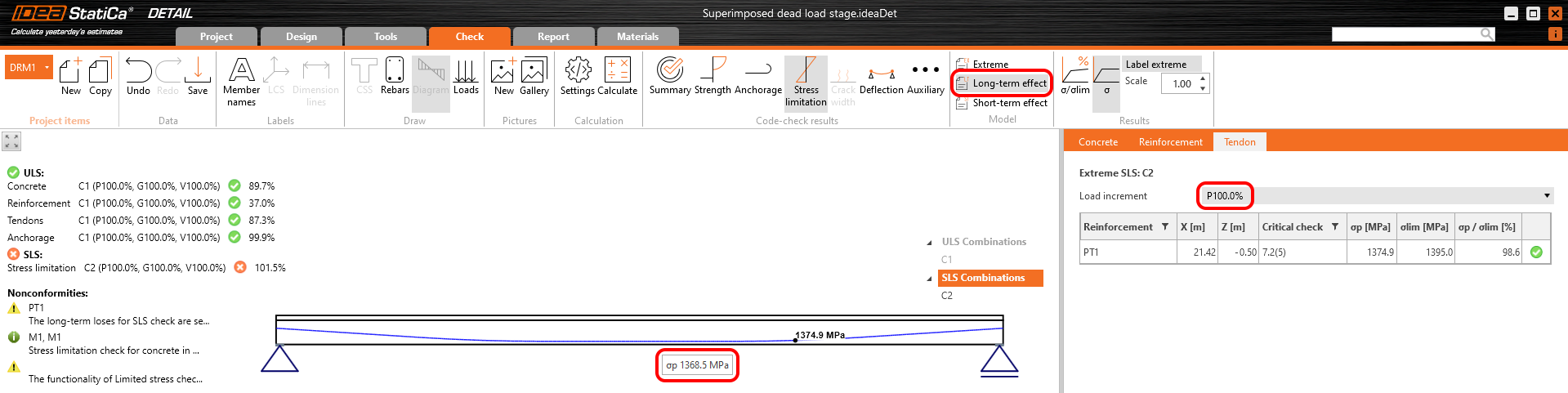
Stress in tendons in SLS:

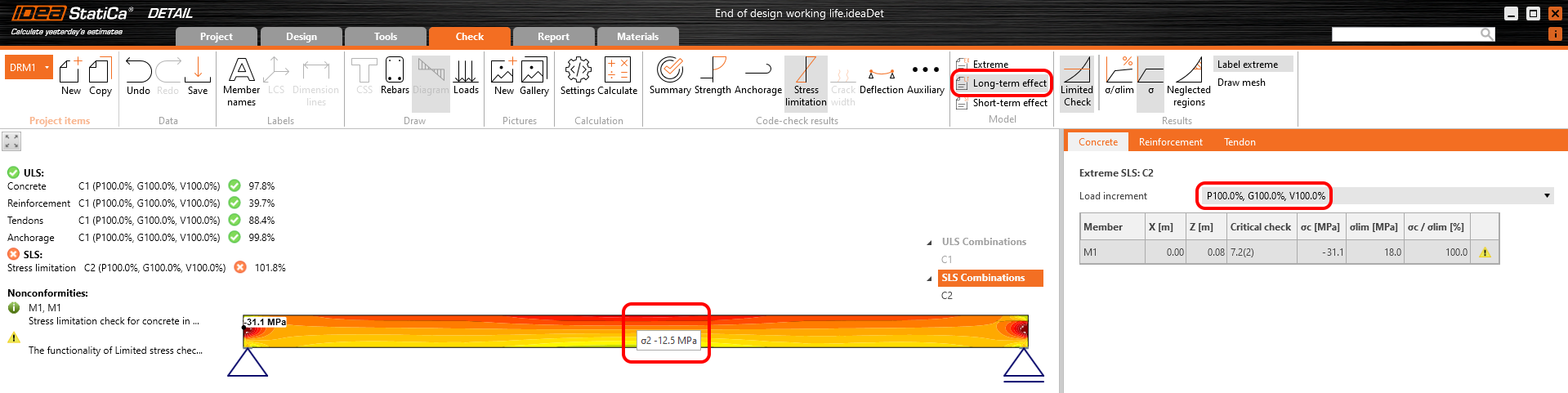
Stress in concrete in SLS:

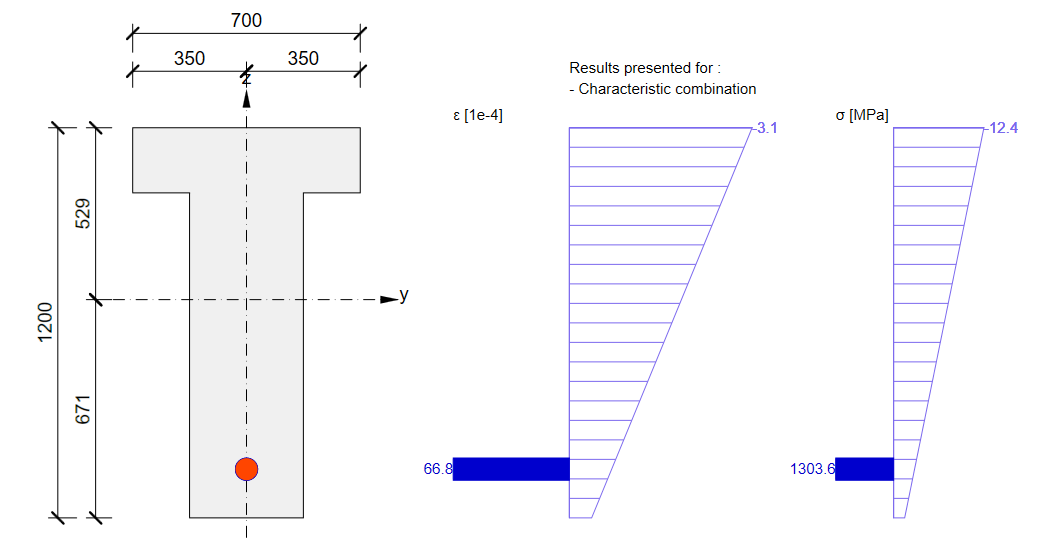
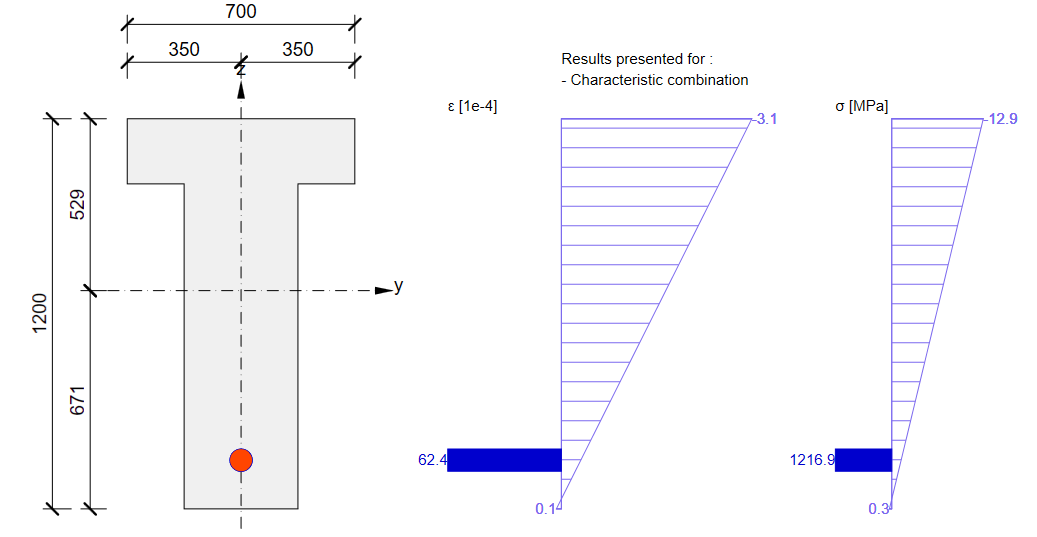
The SLS section check from Beam:

Again, there is a good match. So, it seems we have done the input for this stage correctly. For ULS there will be the same issue described in the previous stage. Note that the coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) was set as 1.0 in the Beam application.

Now recall the beginning of this article where the increments were described. In the Detail application model for this stage, you can go through the individual increments to see the influence of individual load cases. You can also check the short-term effects which will differ from the previous Detail application model for the Transfer of prestressing stage. The reason is the different modulus of elasticity E_cm used in these models. 

What you can actually see in the model for the Superimposed dead load stage in short-term effects is a Transfer of prestressing stage where t=28 days. So, if you don't need to prestress the beam before 28 days you don't need to create a special model for the design of prestressed concrete beams in the Transfer of prestressing stage.

End of design working life

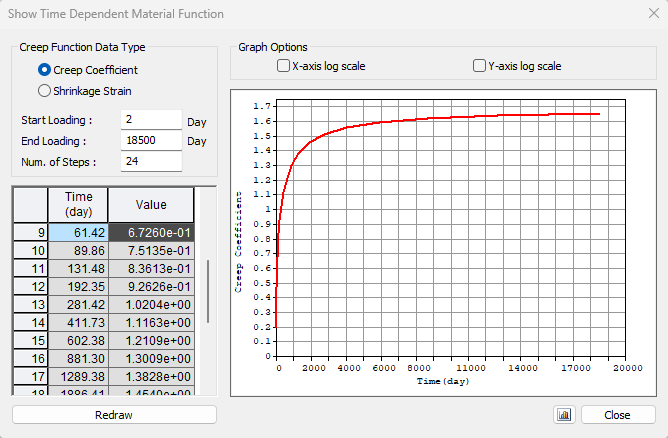
The approach will be the same as for the previous stage. First, we need to determine creep coefficients. In the following figure, you can see the creep coefficient function. 

The value φ_pres ≈ 1.65 for the time from 2 to 18250 days for cement class R according to the Eurocode. The value φ_perm = φ_(18250) - φ₍₆₀₎ ≈ 1.65 - 0.65 = 1.00 for the time from 60 to 18250 days. Note the highlighted value φ₍₆₀₎ in the table above. 

Then we need to look at the value of σ_pa again. We have already confirmed that the values are the same in Beam and Detail.

The long-term losses can be calculated as σ_∞ / σ_pa = 1185 / 1368.6 = 0.865 -> long-term loss is 13.5%. The value of σ_∞ is determined in The beam parameters chapter in the Tendon Stress/Losses chart. Let's input the value and compare the results.

Stress in tendons in SLS:

Stress in concrete in SLS:

The SLS section check from Beam:

Conclusion

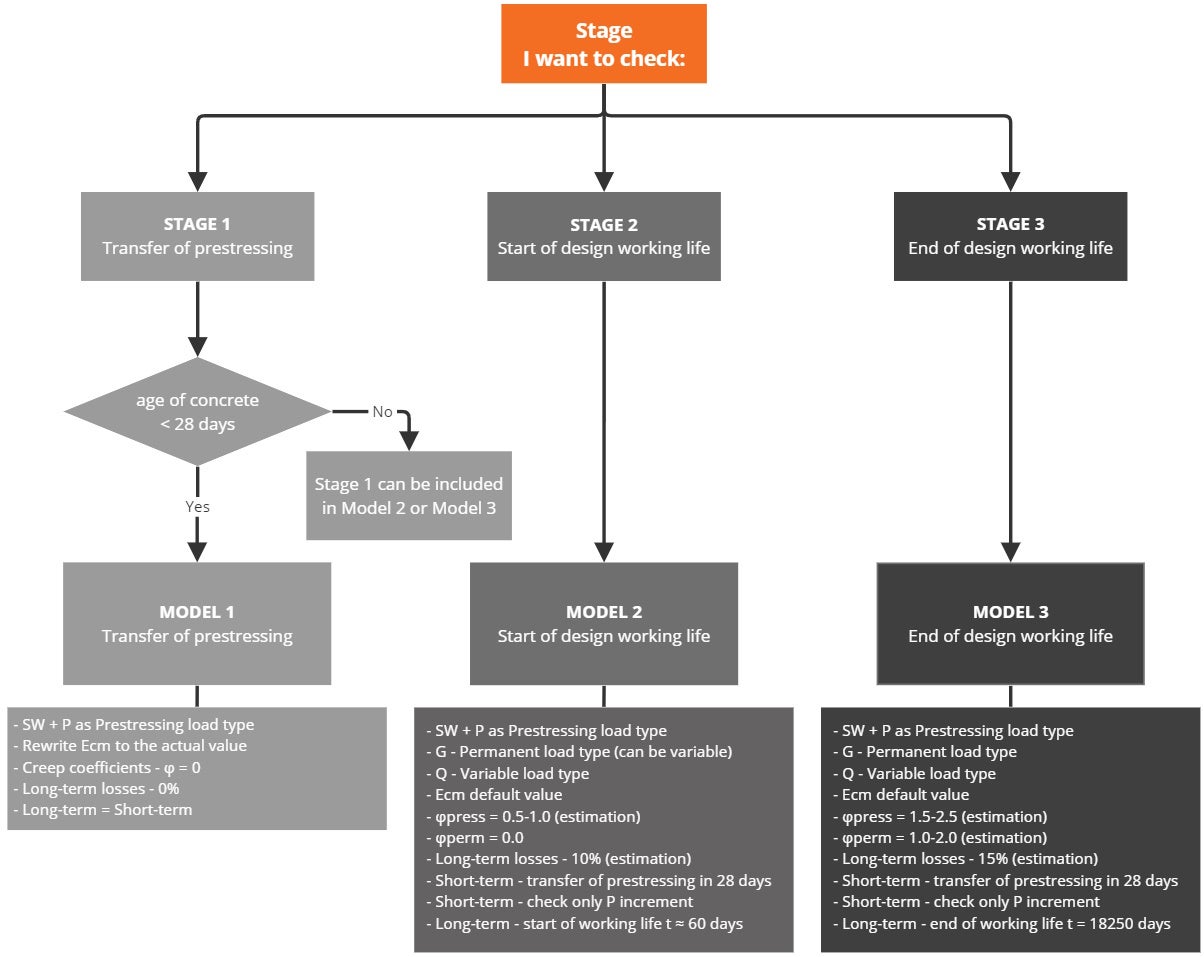
Finally, here is a simple workflow, where you can find the above-described procedure of designing the prestressed concrete structures in IDEA StatiCa Detail using post-tensioned tendons.

It's worth repeating that for post-tensioned tendons the anchorage stress or stress after short-term losses (user-defined type) has to be input. An estimation of the long-term losses due to creep, shrinkage, and relaxation should be input.

Note that in the attached Detail application models for Stage 2 and Stage 3 checks for short-term V increments are unsatisfactory. It follows from the preceding that for Model 2 and Model 3 for short-term effects, only the first increment P needs to be considered (since no other permanent loads, nor variable loads will be applied during applying prestressing). It is valid only if the age of concrete when applying prestressing is greater than 28 days, otherwise, you have to do a special model for Stage 1 (for short-term effects). 

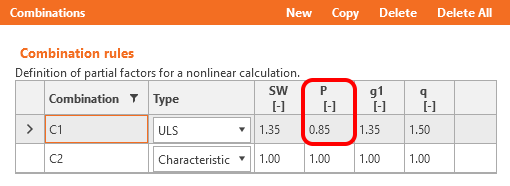
Long-term losses for ULS have to be set as a combination factor. The estimation of long-term losses which can be set in reinforcement is taken into account only for SLS checks. The input for the estimation of 15% should look like this:

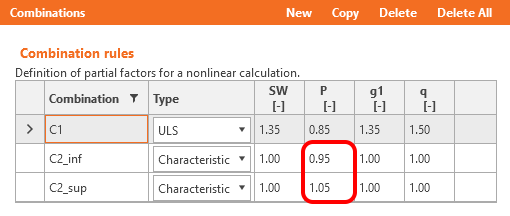
Coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) for prestressing effects for SLS should be also taken into account in combinations. It means you should create at least two combinations. See the figure.

Read about the implementation of these coefficients in the Beam application in How the r_inf and r_sup coefficients are taken into account for SLS checks

You have read how to use IDEA StatiCa Detail a concrete design software where you can, among other things, do a design of prestressed concrete beams with discontinuities. But let's not forget about the IDEA StatiCa Beam, which is used for concrete beam design including TDA, and which we used for comparing the results.

Attached Downloads

• Superimposed dead load stage.ideaDet (IDEADET, 15 kB)
• End of design working life.ideaDet (IDEADET, 15 kB)
• Beam model.ideaBeam (IDEABEAM, 848 kB)
• Transfer of prestressing stage.ideaDet (IDEADET, 15 kB)