Comparison of GMNIA results in IDEA Member to an analytical solution
1. The objective
The objective of this article is the verification of the GMNIA (geometrically and materially nonlinear analysis with imperfections) module of the IDEA Member application. The resulting resistances from IDEA Member are compared to EN 1993-1-1 [1] analytical solution for columns in compression.
2. Model description
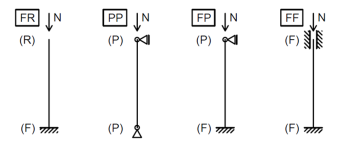
A total of 24 individual cases were analyzed to verify the GMNIA module. All of them share the same cross-section HEB 200 and the same steel grade S 355. Four different boundary conditions were investigated (FF; PP; FP; FF), each with varying values of column relative slenderness (0.5; 1.0; 1.5). Buckling resistance in direction of both principal axes is verified.
Fig. 1: Various boundary conditions used for verification
All cases are designated in the following manner: “FR_0.5_Y”, where “FR” indicates boundary conditions, “0.5” the relative slenderness, and “Y” the buckling axis.
3. Initial imperfections
Three approaches were used to calculate the initial imperfection of a column in compression. These are designated A, B and C.
Approach A – according to EN 1993-1-1:2005, Table 5.1
Tab. 1: Design value of initial bow imperfection e0/L for members
Approach B – according to prEN 1993-1-1:2020, second draft [2], Clause 5.3.3.1
\[ \frac{e_0}{L}=\frac{α}{ε} \beta \]
where:
- e0 – initial imperfection
- α – imperfection factor depending on the relevant buckling curve according to 1993-1-1, Table 6.1 [1]
\[\varepsilon = \sqrt{\frac{235}{f_y}}\]
- fy – column yield strength [MPa]
- β – reference relative bow imperfection according to Table 2
- L – member length
Tab. 2: Reference relative bow imperfection
Approach C – EUGLI (Equivalent Unique Global and Local Initial Imperfection) method according to EN 1993-1-1:2005 [1], Clause 5.3.2 (11).
\[ e_0=\alpha (\bar \lambda - 0.2) \frac{M_{Rk}}{N_{Rk}} \]
where
- e0 – initial imperfection
- α – imperfection factor depending on the relevant buckling curve according to 1993-1-1, Table 6.1 [1]
- \( \bar \lambda \)– member relative slenderness
- NRk – characteristic moment resistance of a cross-section
- MRk – characteristic resistance to normal force of a cross-section
This initial imperfection is then adjusted based on the bending moment response of the member to the initial imperfection in the shape of the elastic buckling mode.
Tab. 3: Resulting initial imperfection values – axis y-y
Tab. 4: Resulting initial imperfection values – axis z-z
4. Analytical solution
The following approach according to EN 1993-1-1 [1], Clause 6.3 is used to calculate the column’s buckling resistance:
\[ N_{cr} = \frac{\pi ^2 E I}{L_{cr}^2} \]
\[ \bar \lambda = \sqrt{\frac{A f_y}{N_{cr}}} \]
\[ \phi = 0.5 \left [1 + \alpha \left (\bar \lambda - 0.2 \right ) + \bar \lambda ^2 \right] \]
\[ \chi = \frac{1}{\phi + \sqrt{\phi^2 - \bar \lambda ^2}} \]
\[ N_{b,Rd} = \frac{\chi A f_y}{\gamma_{M1}} \]
5. Results
The ultimate resistances (for initial imperfections A, B, C) from IDEA Member are compared to an analytical value for a rolled cross-section (EN) and for its representation without the web-flange radii (Ew) as well.
5.1 Strong axis buckling
The results for strong axis buckling are summarized in the table below.
Tab. 5: Resulting resistance values – axis y-y
Chart 1: Resulting resistance values – axis y-y
Chart 2: Resulting resistance comparison – axis y-y
The results of GMNIA are conservative compared to the Eurocode solution. This is in part caused by the cross-section modeling in IDEA Member, this influence is under 2 % as can be seen from the blue column values in the chart above.
The initial imperfection choice plays a major role in the resulting resistance. Method C is only slightly conservative (< 4 %), while methods A and B give resistances 10–16 % lower, when compared to the Eurocode analytical solution.
Fig. 2: Column PP_1.0_Y at its resistance limit and flange plastic strain
5.2. Weak axis buckling
The results for weak axis buckling are summarized in the table below.
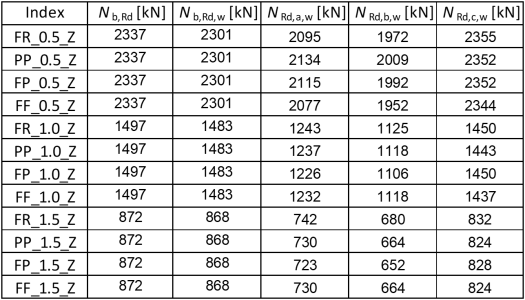
Tab. 6: Resulting resistance values – axis z-z
Chart 3: Resulting resistance values – axis z-z
Chart 4: Resulting resistance comparison – axis z-z
Again, the results are conservative compared to the Eurocode solution. The cross-section modeling influence is under 2 % as can be seen from the blue column values in the chart above.
The initial imperfection chosen according to method C gives only slightly conservative results (< 6 %), while methods A and B give resistances 10–26 % lower when compared to the Eurocode analytical solution.
6. Literature and References
[1] EN 1993-1-1: Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings, CEN, 2005.
[2] prEN 1993-1-1: Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings, second draft, CEN, 2017.