General introduction for the structural design of steel connections
Introduction
Bar members are preferred by engineers when designing steel structures. However, there are many locations on the structure where the theory of members is not valid, e.g., welded joints, bolted connections, footing, holes in walls, the tapering height of cross-section and point loads. The structural analysis in such locations is difficult and it requires special attention. The behavior is non-linear and the nonlinearities must be respected, e.g., yielding of the material of plates, contact between end plates or base plate and concrete block, one-sided actions of bolts and anchors, welds. Design codes, e.g. EN1993-1-8, and also technical literature offer engineering solution methods. Their general feature is derivation for typical structural shapes and simple loadings. The method of components is used very often.
Component method
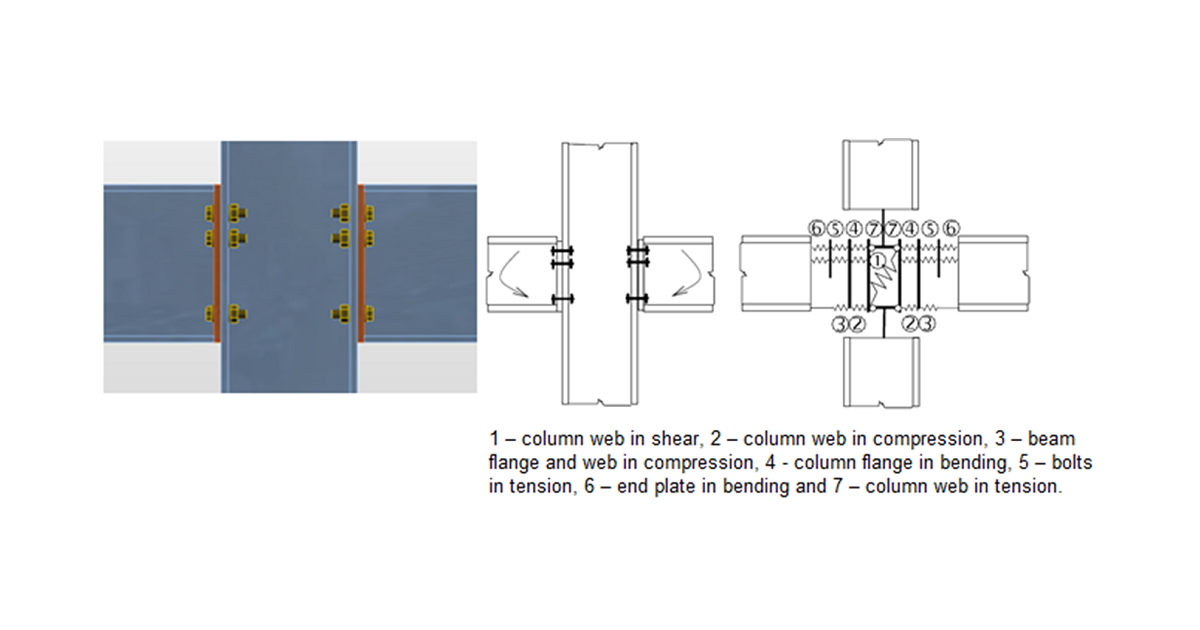
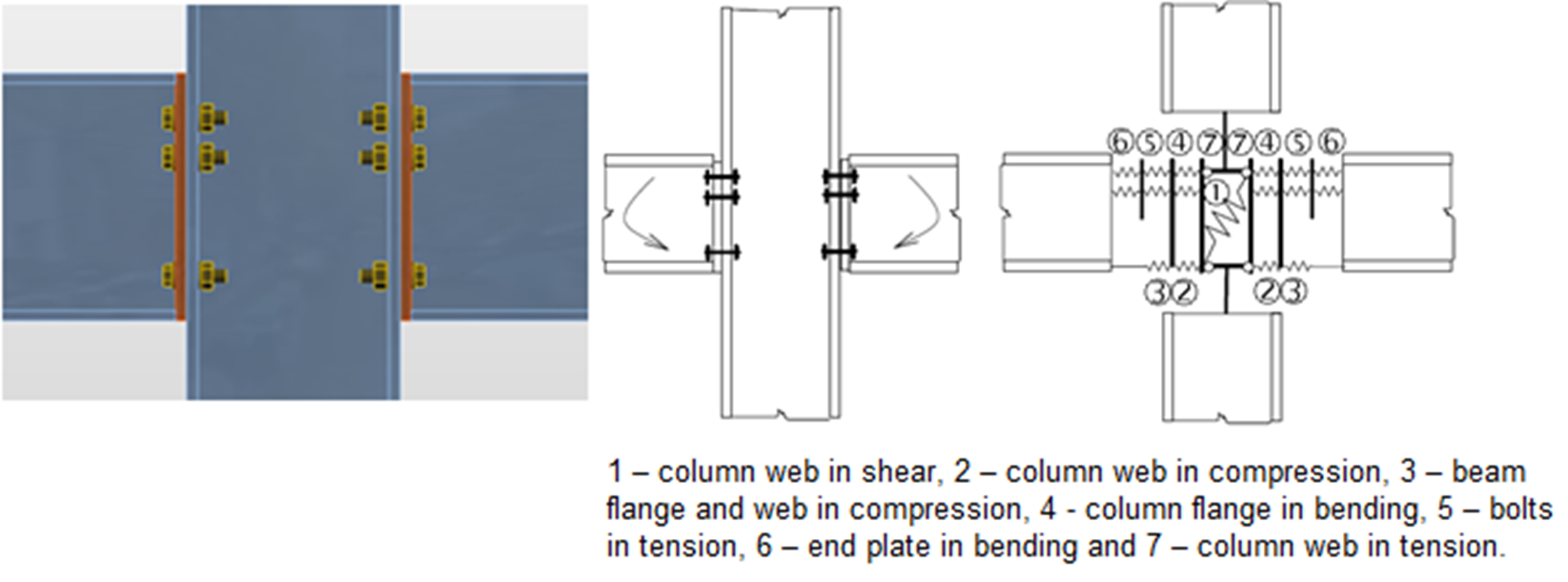
The component method (CM) solves the joint as a system of interconnected items – components. The corresponding model is built per each joint type to be able to determine forces and stresses in each component – see the following picture.
The components of a joint with bolted end plates modeled by springs
Each component is checked separately using corresponding formulas. As the proper model must be created for each joint type, the method usage has limits when solving joints of general shapes and general loads.
IDEA StatiCa together with a project team of Department of Steel and Timber Structures of Faculty of Civil Engineering in Prague and Institute of Metal and Timber Structures of Faculty of Civil Engineering of the Brno University of Technology, developed a method for advanced design of steel structural joints.
Component Based Finite Element Model (CBFEM) method is:
- General enough to be usable for most of the joints, footings, and details in engineering practice.
- Simple and fast enough in daily practice to provide results in a time comparable to current methods and tools.
- Comprehensive enough to provide structural engineer clear information about joint behavior, stress, strain, and reserves of individual components and about overall safety and reliability.
The CBFEM method is based on the idea that most of the verified and very useful parts of CM should be kept. The weak point of CM – its generality when analyzing stresses of individual components – was replaced by modeling and analysis using the Finite Element Method (FEM).
FEM is a general method commonly used for structural analysis. The usage of FEM for modeling of joints of any shapes seems to be ideal (Virdi, 1999). The elastic-plastic analysis is required, as the steel ordinarily yields in the structure. In fact, the results of the linear analysis are useless for joint design.
FEM models are used for research purposes of joint behavior, which usually apply spatial elements and measured values of material properties.
FEM model of a joint for research. It uses spatial 3D elements for both plates and bolts
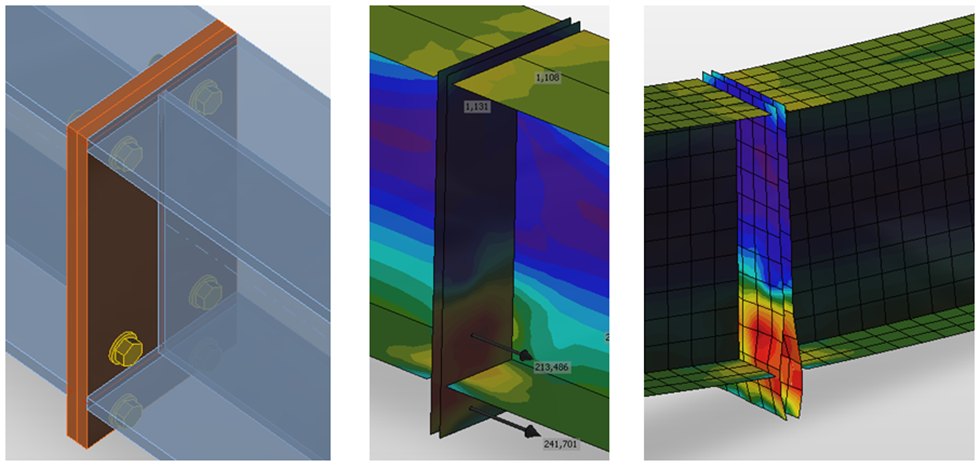
Both webs and flanges of connected members are modeled using shell elements in the CBFEM model for which the known and verified solution is available.
The fasteners – bolts and welds – are the most difficult in the point of view of the analysis model. Modeling of such elements in general FEM programs is difficult because the programs do not offer the required properties. Thus, special FEM components had to be developed to model the welds and bolts behavior in a joint.
CBFEM model of bolted connection by end plates
Joints of members are modeled as massless points when analyzing steel frame or girder structure. Equilibrium equations are assembled in joints and internal forces on the ends of beams are determined after solving the whole structure. In fact, the joint is loaded by those forces. The resultant of forces from all members in the joint is zero – the whole joint is in equilibrium.
The real shape of a joint is not known in the structural model. The engineer only defines whether the joint is assumed to be rigid or hinged.
It is necessary to create a trustworthy model of joint, which respect the real state, to design the joint properly. The ends of members with the length of a 2-3 multiple of maximal cross-section height are used in the CBFEM method. These segments are modeled using shell elements.
A theoretical (massless) joint and real shape of the joint without modified member ends
For better precision of the CBFEM model, the end forces on 1D members are applied as loads on the segment ends. Sextuplets of forces from the theoretical joint are transferred to the end of the segment – the values of forces are kept, but the moments are modified by the actions of forces on corresponding arms.
The segment ends at the joint are not connected. The connection must be modeled. So-called manufacturing operations are used in the CBFEM method to model the connection. Manufacturing operations are especially: cuts, offsets, holes, stiffeners, ribs, end plates and splices, cleats, gusset plates, and others. Fastening elements (welds and bolts) are also added.
IDEA StatiCa Connection can perform two types of analysis:
- Geometrically linear analysis with material and contact nonlinearities for stress and strain analysis,
- Eigenvalue analysis to determine the possibility of buckling.
In the case of connections, the geometrically nonlinear analysis is not necessary unless plates are very slender. Plate slenderness can be determined by eigenvalue (buckling) analysis. For the limit slenderness where geometrically linear analysis is still sufficient, see Chapter 3.9. The geometrically nonlinear analysis is not implemented in the software.