Internal forces in the steel connections
The end forces of a member of the frame analysis model are transferred to the ends of member segments. Eccentricities of the members caused by the joint design are respected during transfer.
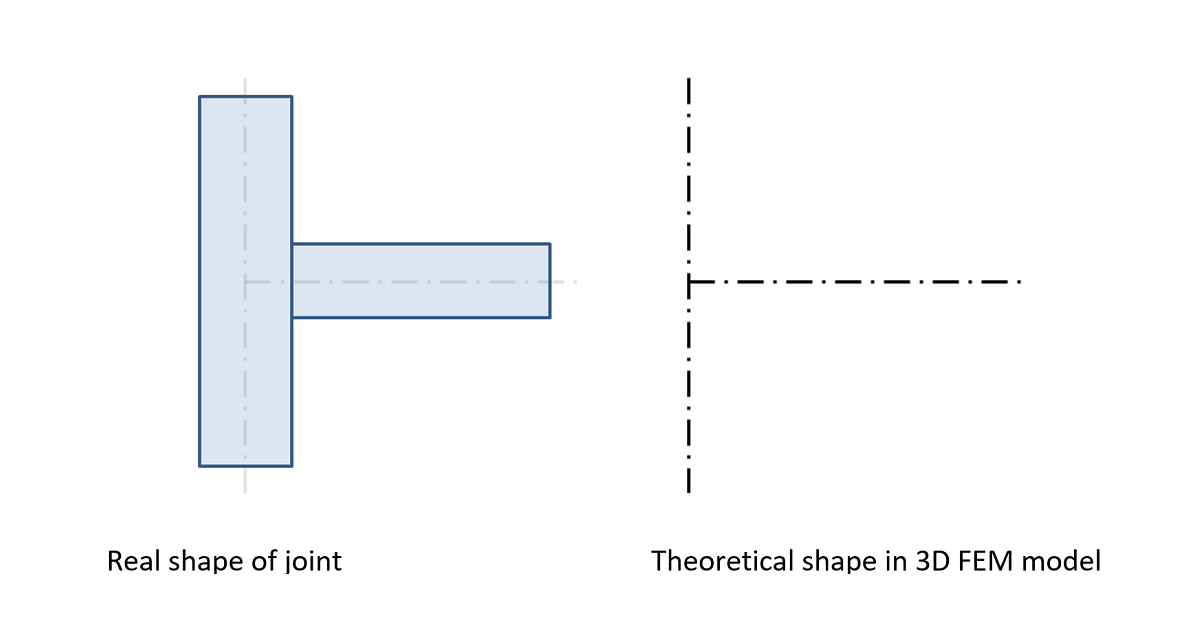
The analysis model created by the CBFEM method corresponds to the real joint very precisely, whereas the analysis of internal forces is performed on a much idealized 3D FEM bar model, where individual beams are modeled using center lines, and the joints are modeled using immaterial nodes.
Joint of a vertical column and a horizontal beam
The internal forces are analyzed using 1D members in the 3D model. There is an example of the internal forces in the following figure.
Internal forces in horizontal beam; M and V are the end forces at joint
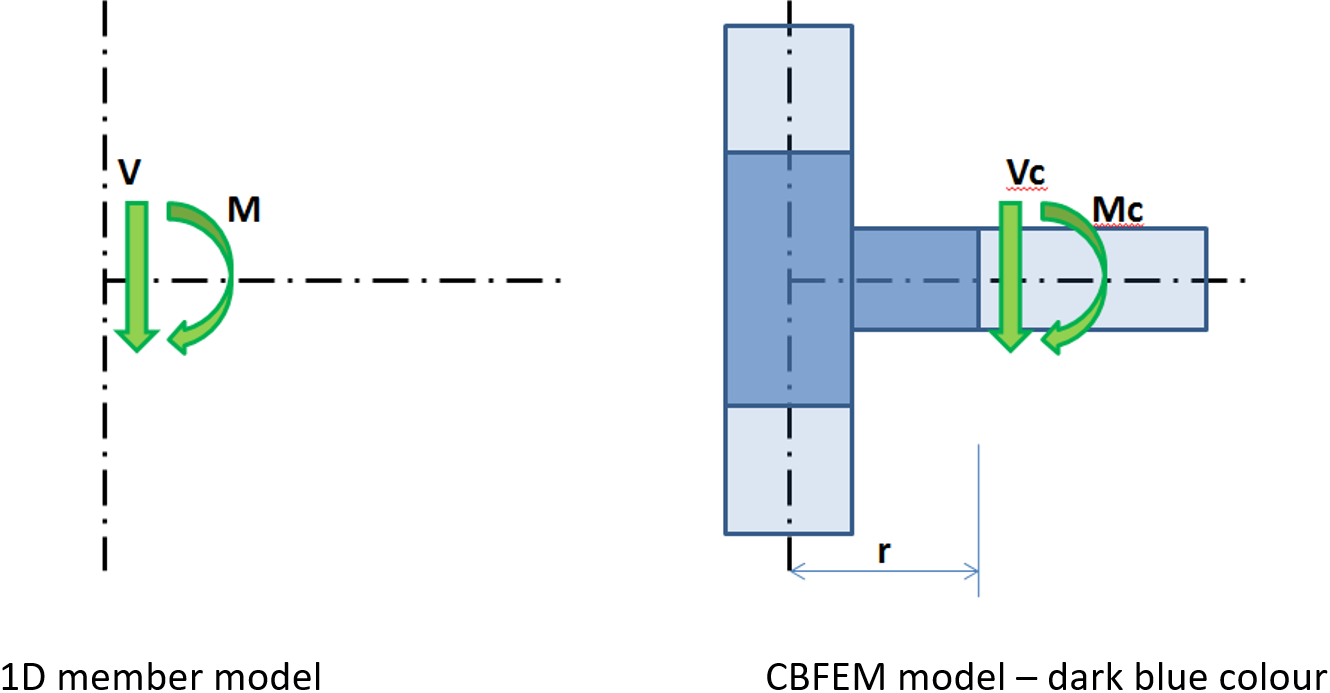
The effects caused by a member on the joint are important to designing the joint (connection). The effects are illustrated in the following figure:
Effects of the member on the joint; CBFEM model is drawn in dark blue color
Moment M and shear force V act in the theoretical joint. The point of the theoretical joint does not exist in the CBFEM model, thus the load cannot be applied here. The model must be loaded by actions M and V, which have to be transferred to the end of the segment in the distance r
Mc = M – V ∙ r
Vc = V
In the CBFEM model, the end section of the segment is loaded by moment Mc and force Vc.
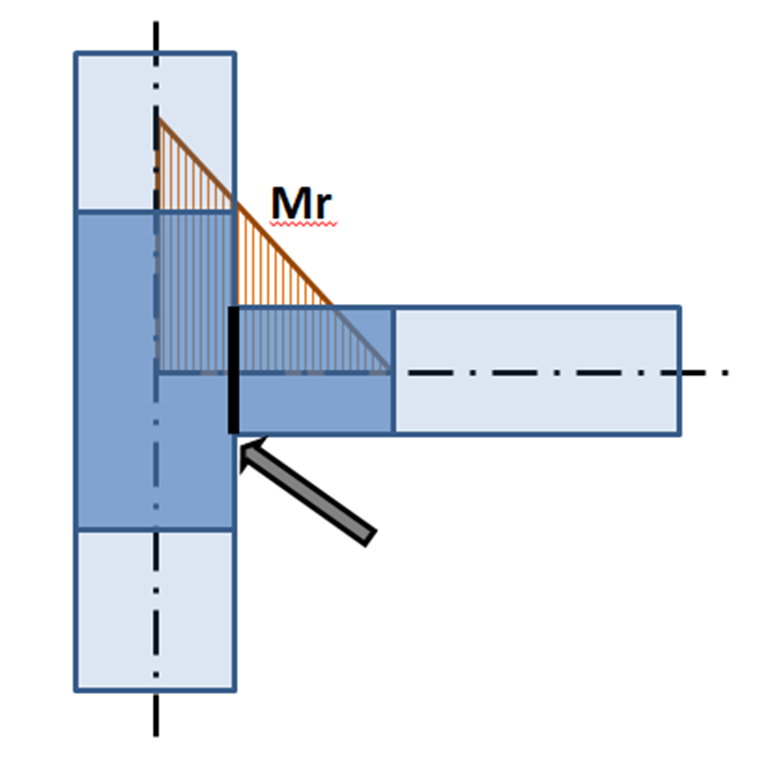
When designing the joint, its real position relative to the theoretical point of the joint must be determined and respected. The internal forces in the position of the real joint are mostly different from the internal forces in the theoretical point of joint. Thanks to the precise CBFEM model, the design is performed on reduced forces – see moment Mr in the following figure:
Bending moment on CBFEM model: The arrow points to the real position of the connection
When loading the joint, it must be respected that the solution of the real joint must correspond to the theoretical model used for the calculation of internal forces. This is fulfilled for rigid joints, but the situation may be completely different for hinges.
Position of hinge in theoretical 3D FEM model and in the real structure
It is illustrated in the previous figure that the position of the hinge in the theoretical 1D members model differs from the real position in the structure. The theoretical model does not correspond to reality. When applying the calculated internal forces, a significant bending moment is applied to the shifted joint, and the designed joint is overlarge or cannot be designed either. The solution is simple – both models must correspond. Either the hinge in 1D member model must be defined in the proper position, or the shear force must be shifted to get a zero moment in the position of the hinge.
Shifted distribution of bending moment on beam: zero moment is at the position of the hinge
The shift of the shear force can be defined in the table for the definition of the internal force.
The location of the load effect has a big influence on the correct design of the connection. To avoid all misunderstandings, we allow the user to select from three options – Node / Bolts / Position.
Note that when selecting the Node option, the forces are applied at the end of a selected member, which is usually at the theoretical node unless the offset of the selected member is set in geometry.
Import loads from FEA programs
IDEA StatiCa enables to import of internal forces from third-party FEA programs. FEA programs use an envelope of internal forces from combinations. IDEA StatiCa Connection is a program that resolves steel joint nonlinearly (elastic/plastic material model). Therefore, the envelope combinations cannot be used. IDEA StatiCa searches for extremes of internal forces (N, Vy, Vz, Mx, My, Mz) in all combinations at the ends of all members connected to the joint. For each such extreme value, also all other internal forces from that combination in all remaining members are used. Idea StatiCa determines the worst combination for each component (plate, weld, bolt etc.) in the connection.
The user can modify this list of load cases. He can work with combinations in the wizard (or BIM), or he can delete some cases directly in IDEA StatiCa Connection.
Warning!
It is necessary to take into account unbalanced internal forces during the import. This can happen in the following cases:
- Nodal force was applied to the position of the investigated node. The software cannot detect which member should transfer this nodal force and, therefore, it is not taken into account in the analysis model. Solution: Do not use nodal forces in global analysis. If necessary, the force must be manually added to a selected member as a normal or shear force.
- Loaded, non-steel (usually timber or concrete) member is connected to the investigated node. Such member is not considered in the analysis, and their internal forces are ignored in the analysis. Solution: Replace the concrete member with a concrete block and anchorage.
- The node is a part of a slab or a wall (usually from concrete). The slab or the wall is not part of the model, and its internal forces are ignored. Solution: Replace the concrete slab or wall with a concrete block and anchorage.
- Some members are connected to the investigated node via rigid links. Such members are not included in the model, and their internal forces are ignored. Solution: Add these members into the list of connected members manually.
- Seismic load cases are analyzed in the software. Most FEA software offer the modal analysis to solve seismicity. The results of internal forces of seismic load cases provide usually only internal force envelopes in sections. Due to the evaluation method (square root of the sum of squares – SRSS), the internal forces are all positive and it is not possible to find the forces matching to the selected extreme. It is not possible to achieve a balance of internal forces. Solution: Change the positive sign of some internal forces manually.