How to include creep in a concrete slender column in Member
When designing slender reinforced concrete elements, the effects of imperfections, second order, and creep on transverse deformation have to be considered.
For a better understanding of the example on which the problem will be explained go through the tutorial Concrete slender column (EN).
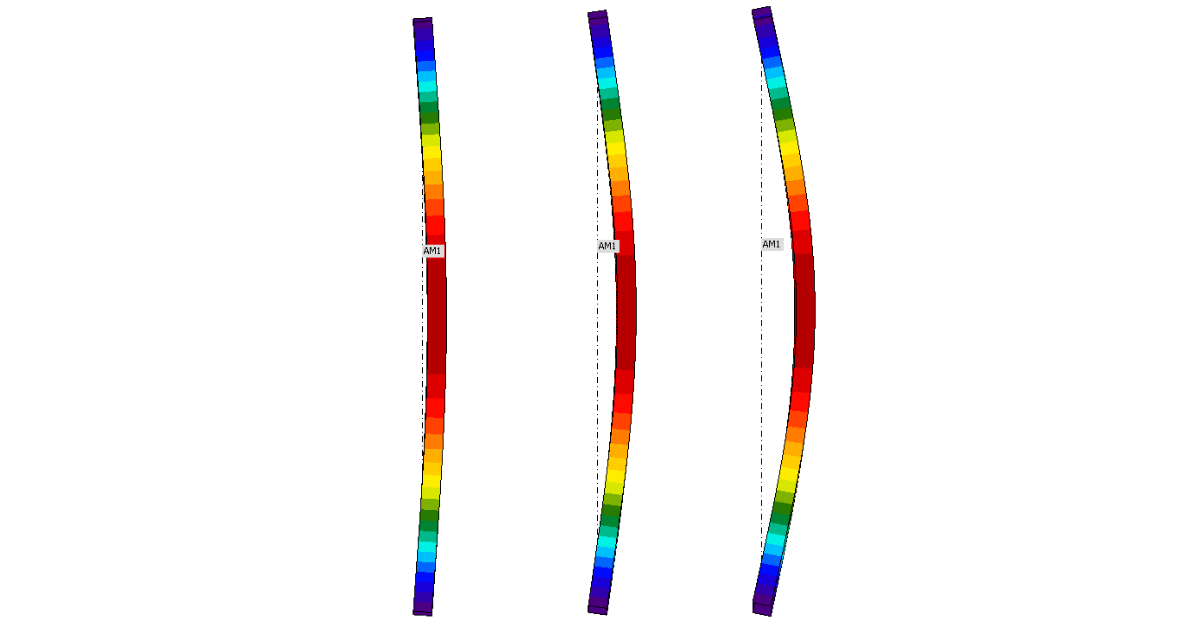
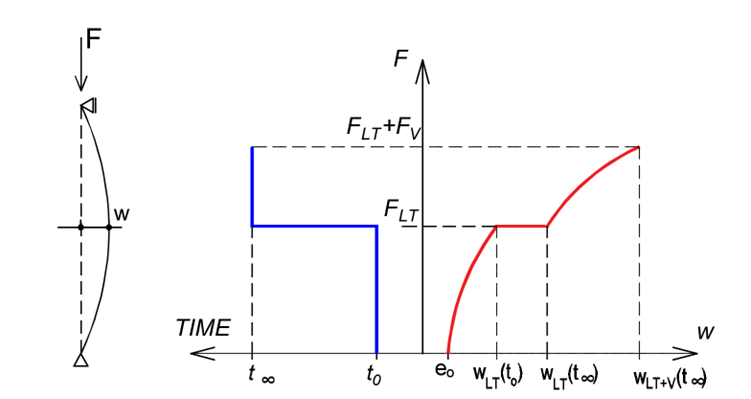
The development of the transverse deformation of the compressed element is shown schematically in the figure above. The total load is composed of a long-term load FLT and a short-term load FV (variable load). Before loading begins, only the geometric imperfection e0 forms the transverse deflection of the element. Once the element is loaded with the FLT force, the transverse deformation increases to wLT(t0). Due to the creep, the transverse deflection will increase to wLT(t∞) in the <t0;t∞> time interval. The total transverse deflection at the end of the life of the structure (time t∞) after the application of the short-term load FV is then wLT+V(t∞). The second-order effect caused by this deflection governs the design of a slender compression member.
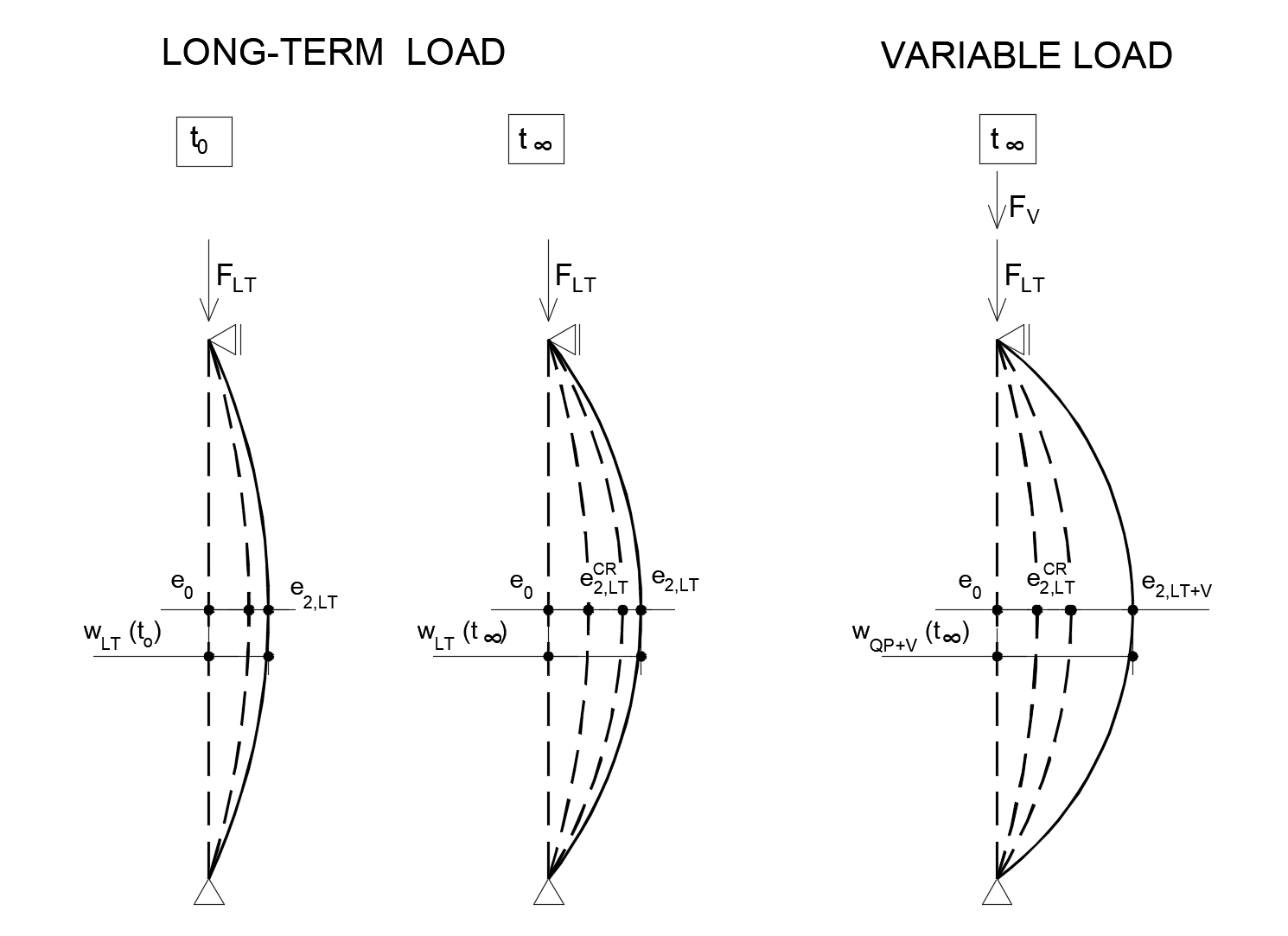
The individual components of the lateral deflection are shown schematically in the following figure.
Where:
e0 initial geometric imperfection defined by the design standard
e2,LT(t0) second order effect from a permanent FLT load, in time t0. This deflection also includes the effect
of transverse loads or end moments. The value is the result of a GMNIA calculation in the member
(Ux or Uy displacement), where the initial imperfection is set to e0
e2,LTCR(t∞) the increment to e2,LT(t) that is caused by concrete creep in the time interval <t0;t∞>.
e2,LT+V second order effect at time t∞ from constant (LT) and variable (V) loads. This value is automatically
taken into account by the program using the GMNIA calculation, where the imperfection is given by
e0 + e2,LTCR(t∞).
For the design of the compressed element, a value of e2,LTCR(t∞) is required. As deflection e2,LTCR(t∞) increases over time, deflection e2,LT(t) will increase simultaneously. To accurately calculate the final value of e2,LTCR(t∞), it would be necessary to use a time-dependent analysis (TDA). In the current version, the program does not calculate this automatically and it must be determined manually by an iterative procedure, which is discussed below.
The calculation steps in the member program are as follows:
- GMNIA calculation of the response of the member to long-term loads FLT with specified initial imperfection e0.
- Determination of total imperfection e0 + e2,LTCR(t∞)
- GMNIA calculation of the response of the member to total load FLT + FV , with total imperfection e0 + e2,LTCR(t∞) specified in the program
Determination of the deflection e2,LTCR(t∞):
For the total deflection from permanent FLT loads at the end of life at time t∞:
wLT(t∞) = e0 + e2,LTCR(t∞) + e2,LT(t∞)
Conservatively:
e2,LTCR(t∞) = φ(t0,t∞) * e2,LT(t∞) where φ(t0,t∞) is a creep coefficient
The value of e2,LT(t∞) is determined by a GMNIA calculation with the total specified imperfection e0 + e2,LTCR(t∞) = e0 + φ(t0,t∞) * e2,LT(t∞). Clearly, for this simplified and conservative approach, the value of e2,LT(t∞) "depends on itself" and has to be determined by iteration.
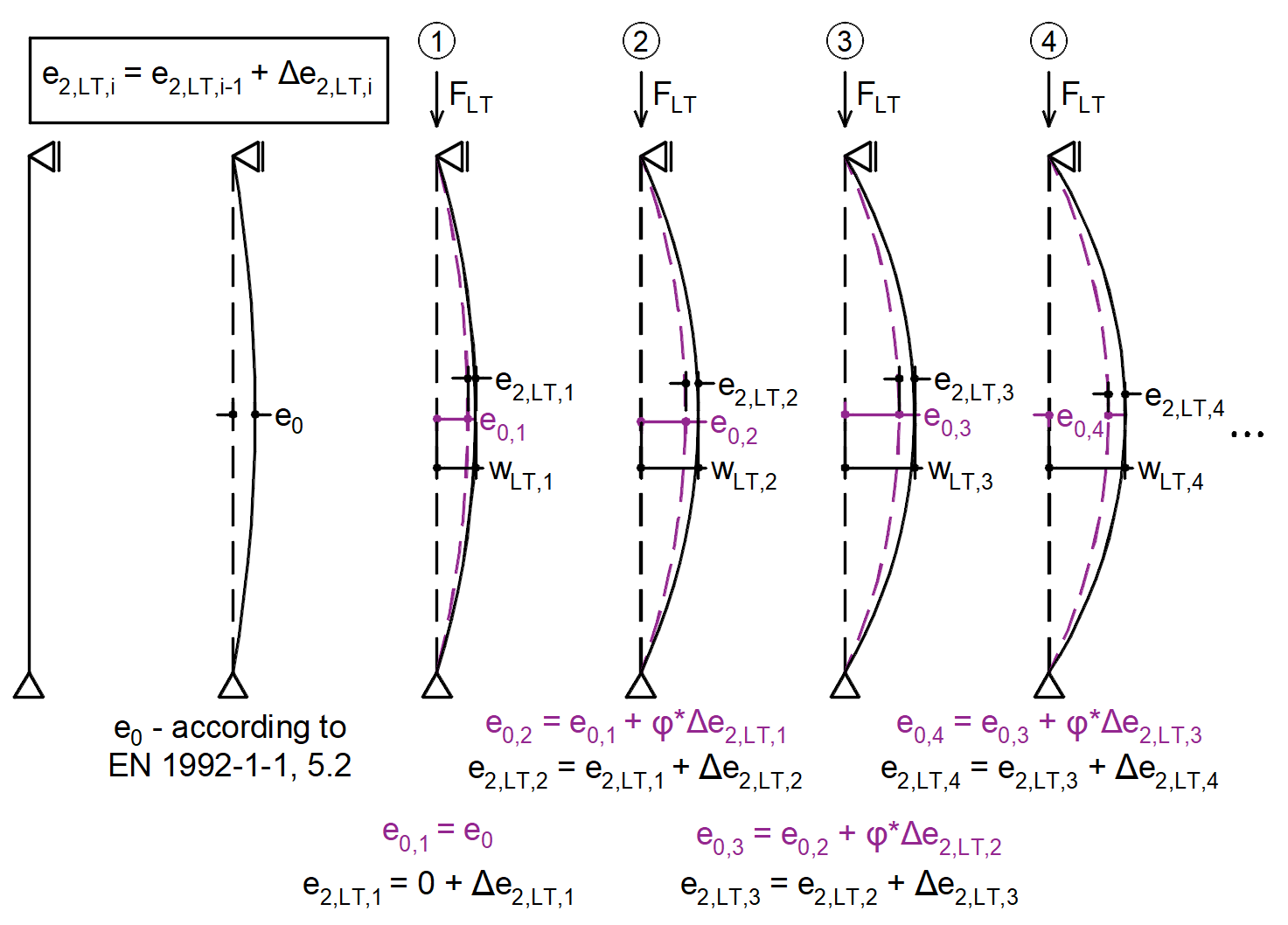
You can iterate sequentially as shown below. The four steps of the iteration are shown. The variable labels are slightly different to keep the picture simple.
φ(t0,t∞) = φ
e2,LT(t∞) = e2,LT,i
wLT(t∞) = wLT,i
The video tutorial of gradual iteration described above is shown below. The excel file used in this tutorial is also attached.
Note: The load case LE4 contains only long-term loads (quasi-permanent combination) and is applied as a ULS load type. This means that the ULS material model is used to calculate the initial imperfection.
Try IDEA StatiCa for free
Attached Downloads
- Member creep (ZIP, 9 kB)