Knowledge base

How to define correct load position (Forces in)

Steel

Connection

Bolts

Load effects

This article is also available in:

When modeling hinged connections, it is necessary to ensure that zero bending moment is applied at the location of the intended hinge. This can be achieved by changing the position of the applied load (shear force) to the position of the expected hinge.

Real hinge vs theoretical hinge

To ensure that the computational model is consistent with the actual shape and static behavior of the connection, we need to consider the bending moment shape and the location of the shear force in the connection. We will use a simple example of a horizontal beam connected to a column to show the differences in modeling of the moment and hinged connections.

Moment connection

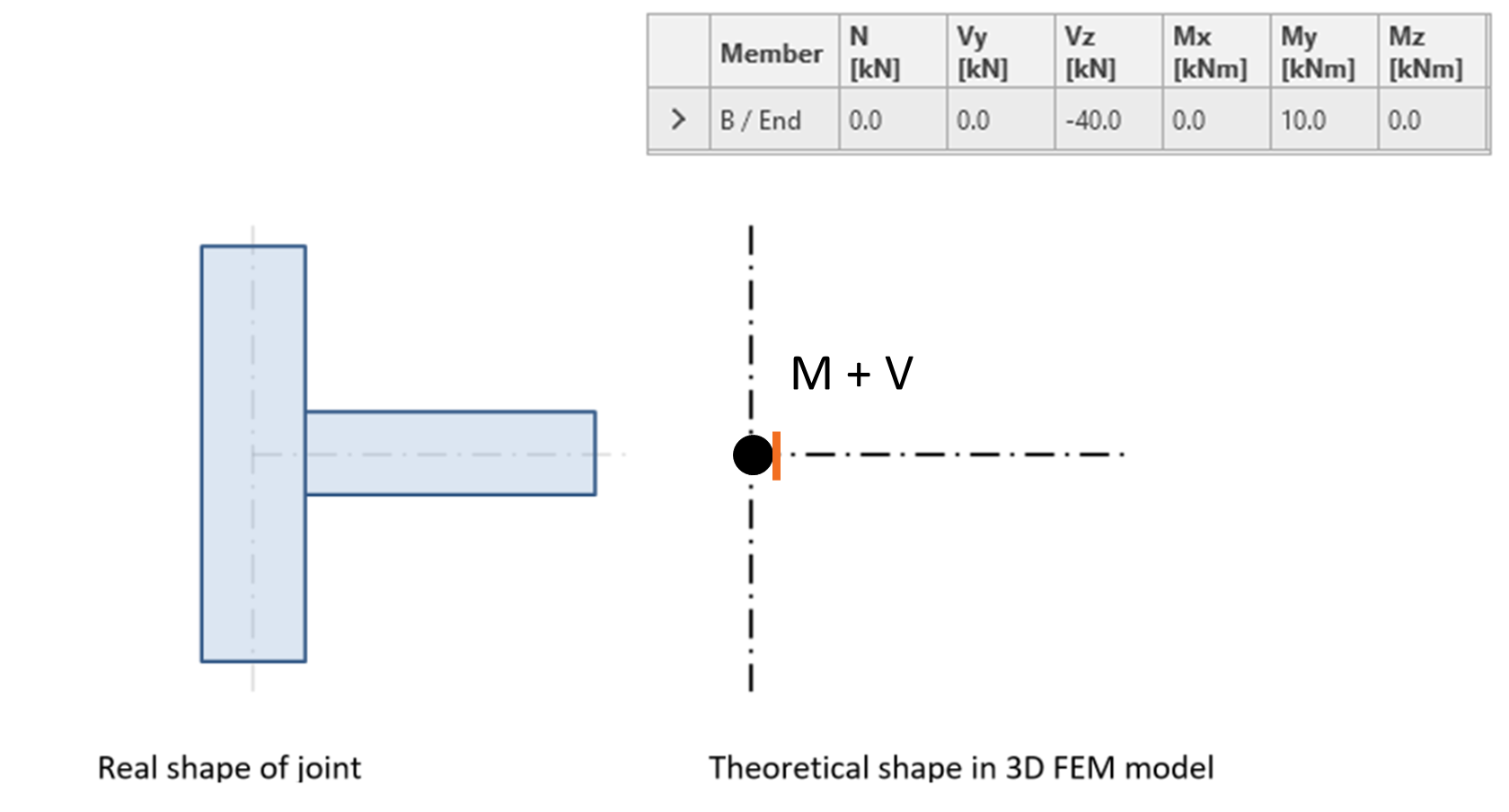
This is a schematic "real" shape of the moment connection (left) and its structural model used for the analysis (right).

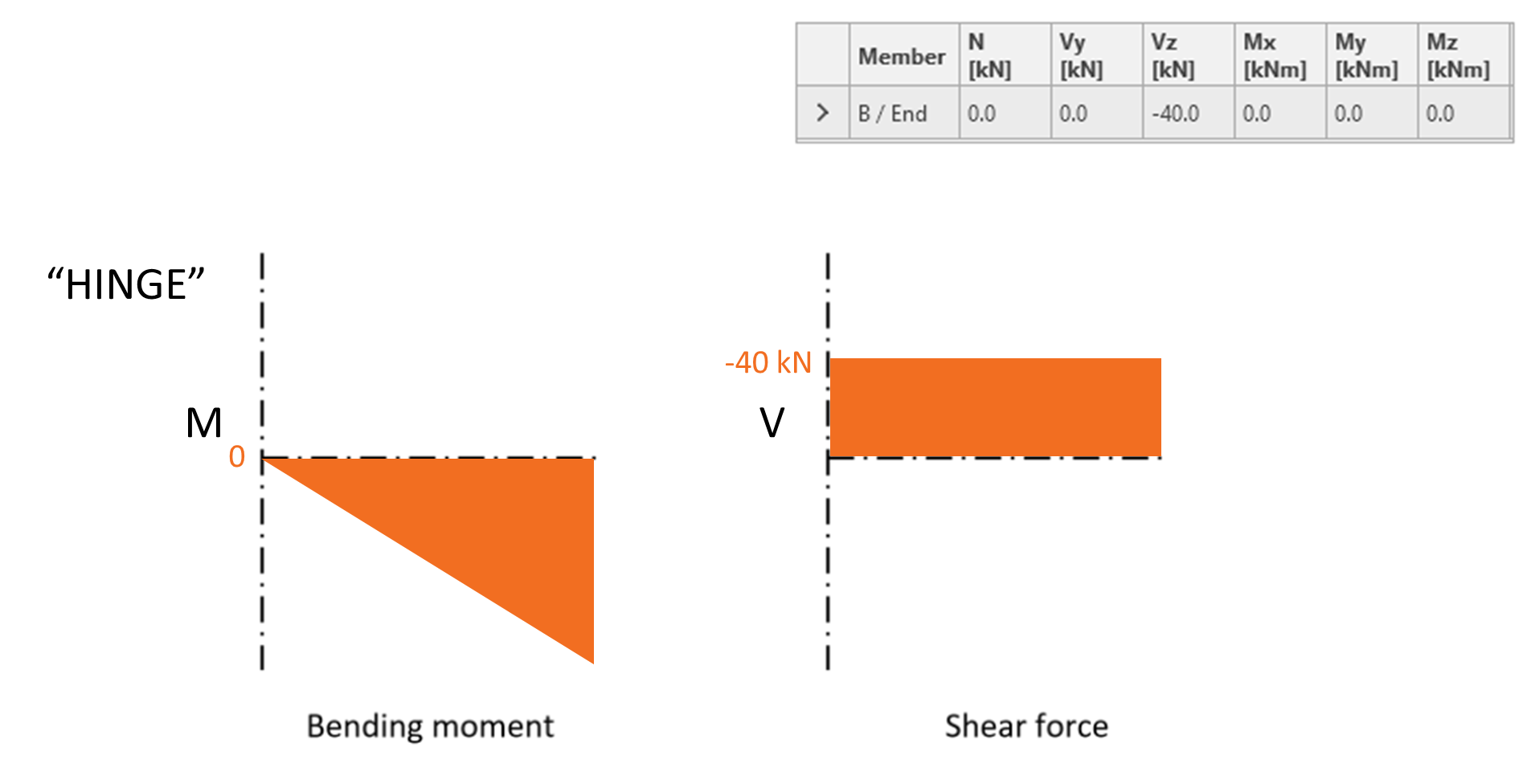
In Load Effects tab in the IDEA StatiCa Connection, we define forces that each member of the connection acts on the node (usually the center of the connection, the intersection of the member axes). The table in the figure above also shows the forces that the horizontal member B acts on the column. The diagrams of the internal forces on the horizontal member are as follows.

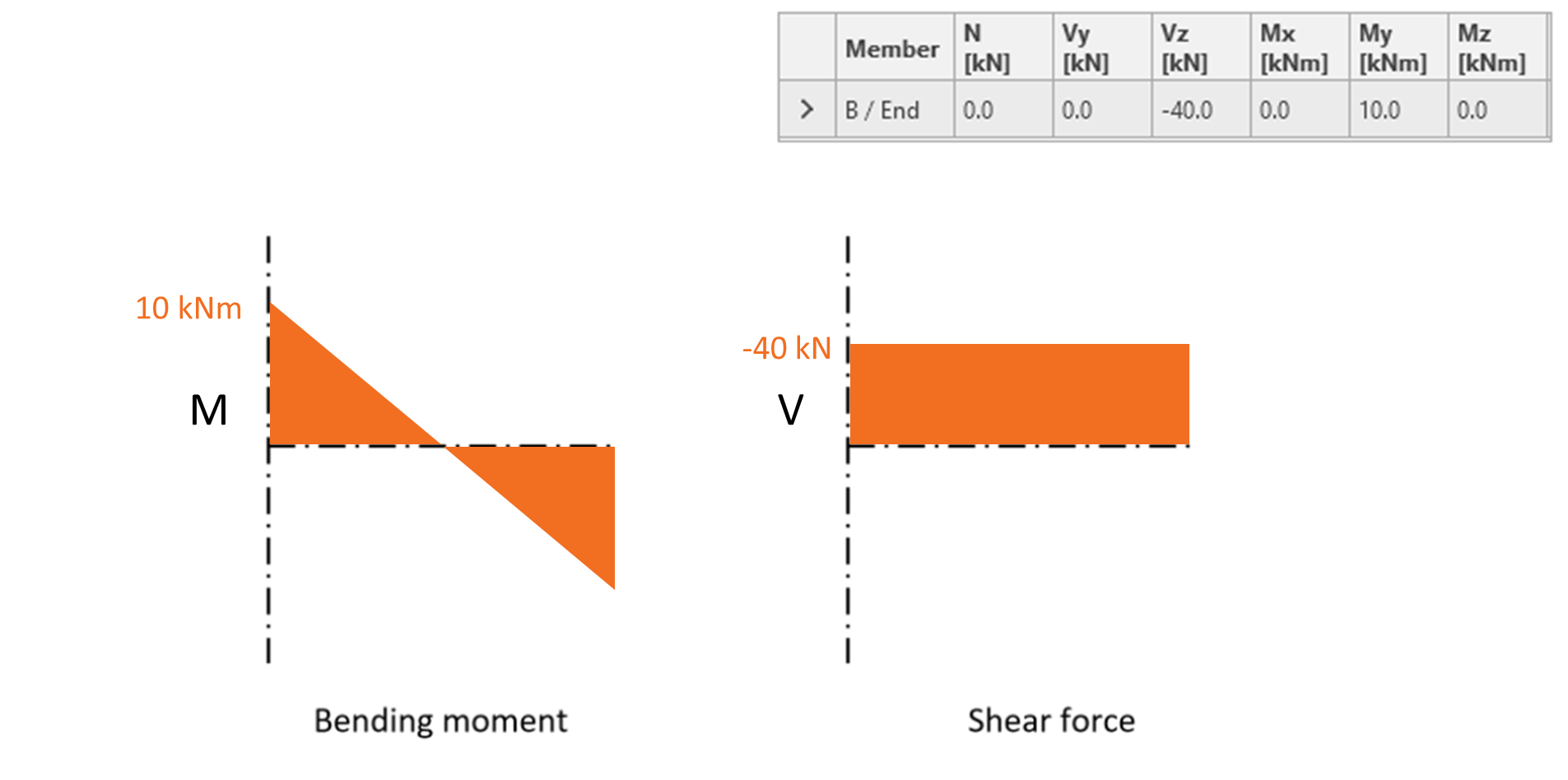
The bending moments along the members are simplified as linear in IDEA StatiCa Connection. At the beginning of the connected member, the specified bending moment is applied and the moment progresses away from the node as a linear function whose slope is defined by the specified shear force.

Watch the video discussing the bending moment distribution and other important information.

Hinged connection

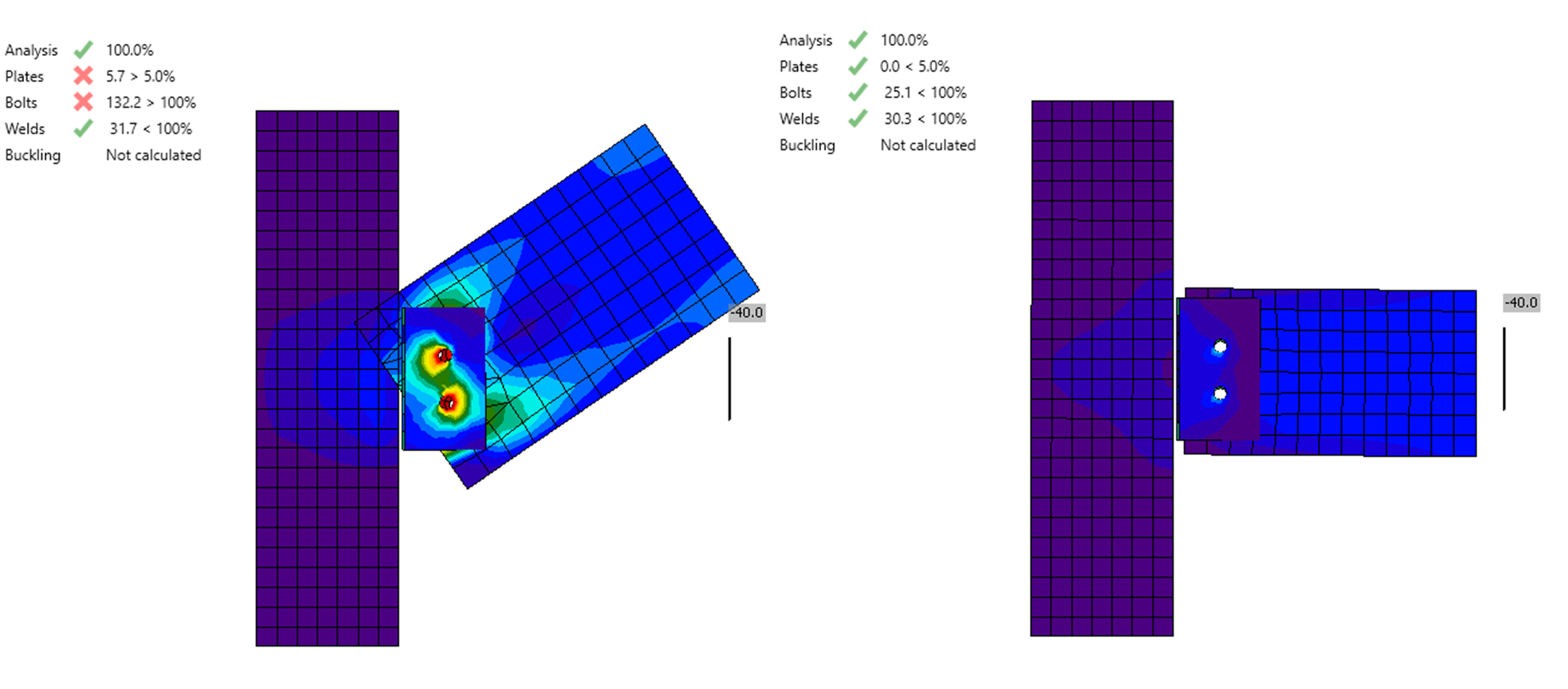
In case of a hinged connection, the bending moment in the connection is zero. Diagrams of the bending moment and shear force in the hinge-connected horizontal member are presented in the following figure. Shear force V_z= -40 kN and zero bending moment M_y must be specified to induce corresponding internal forces in Connection application. In this case, we say that the shear force position (and thus the location of the zero bending moment) is in node (center of the connection).

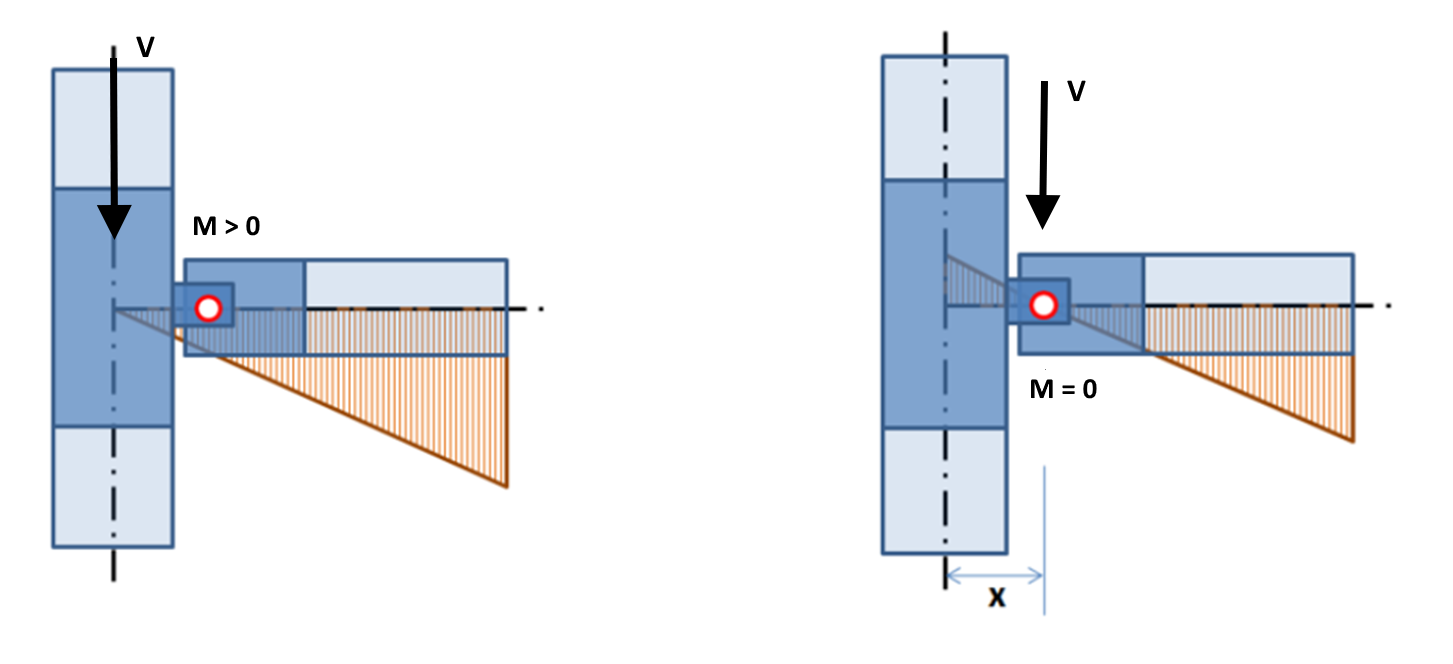
The above figure corresponds to the theoretical situation, where the location of the joint is directly in the node (center of the connection). This is how the hinge connection is normally modeled in a global analysis model. However, in a real structure, the point of rotation (hinge) is shifted from the centre of the joint (node). Consider, for example, a bolted beam-to-column shear connection with a vertical fin plate, where the joint can be assumed to be in the centroid of the bolt group.

As can be seen from the following figure, if the actual position of the joint is not taken into account in the model, a non-zero bending moment is in the location of the real hinge (left in the figure). This is an obvious error. The way to avoid this is to adjust the shear force position (and therefore the zero bending moment location) in the attached element (on the right).

Setting the position of forces

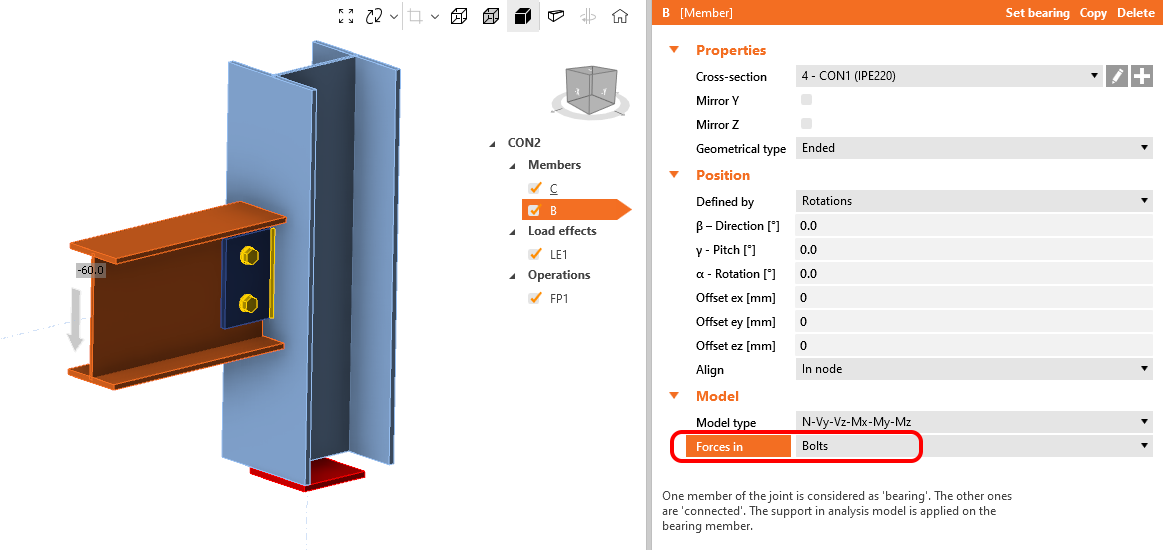
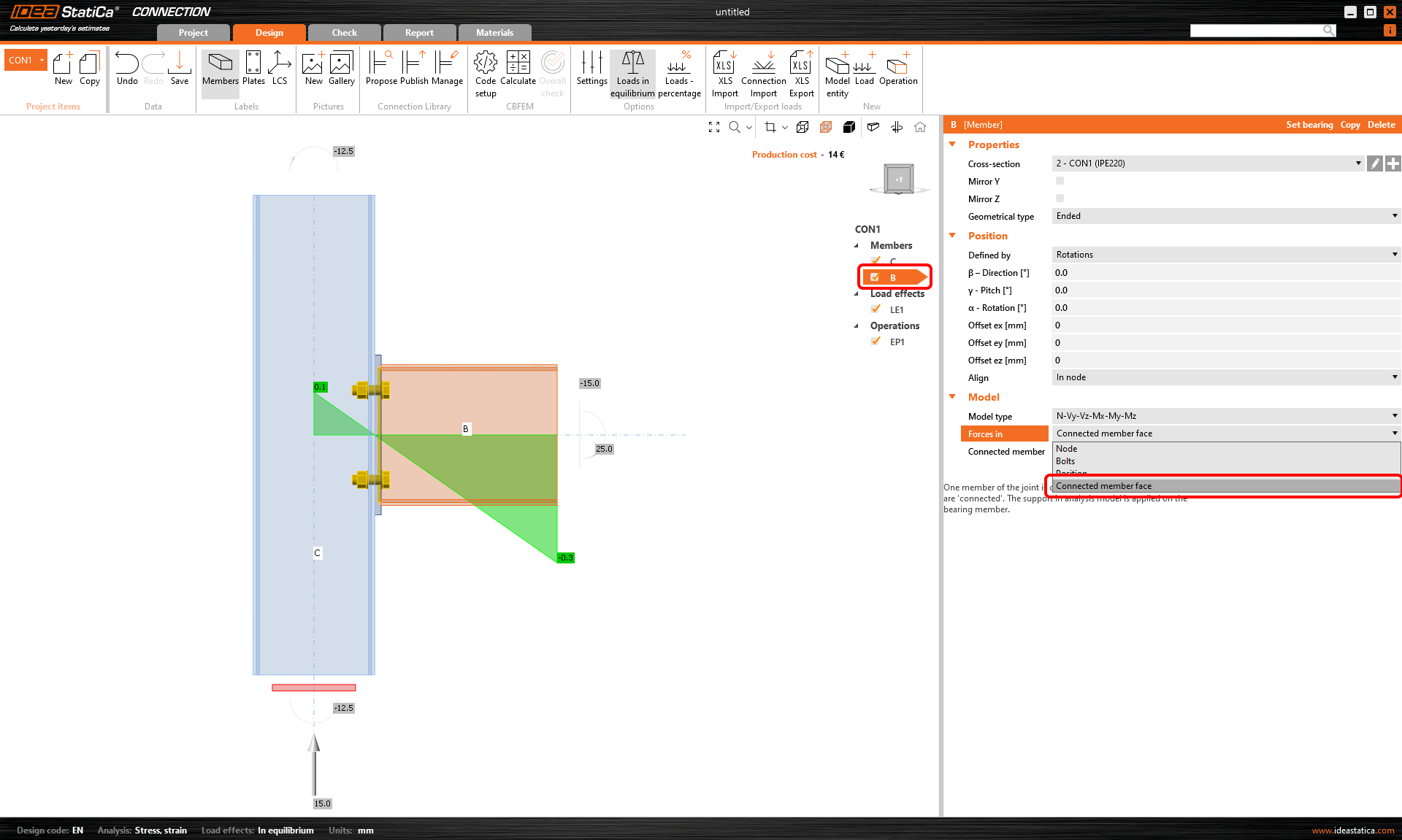
In the application, the position of shear force can be defined in the Model section of the given Member. The difference between these two cases is shown here:

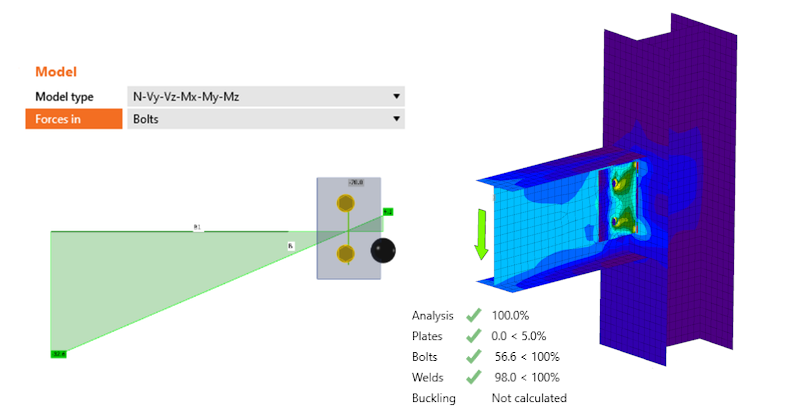
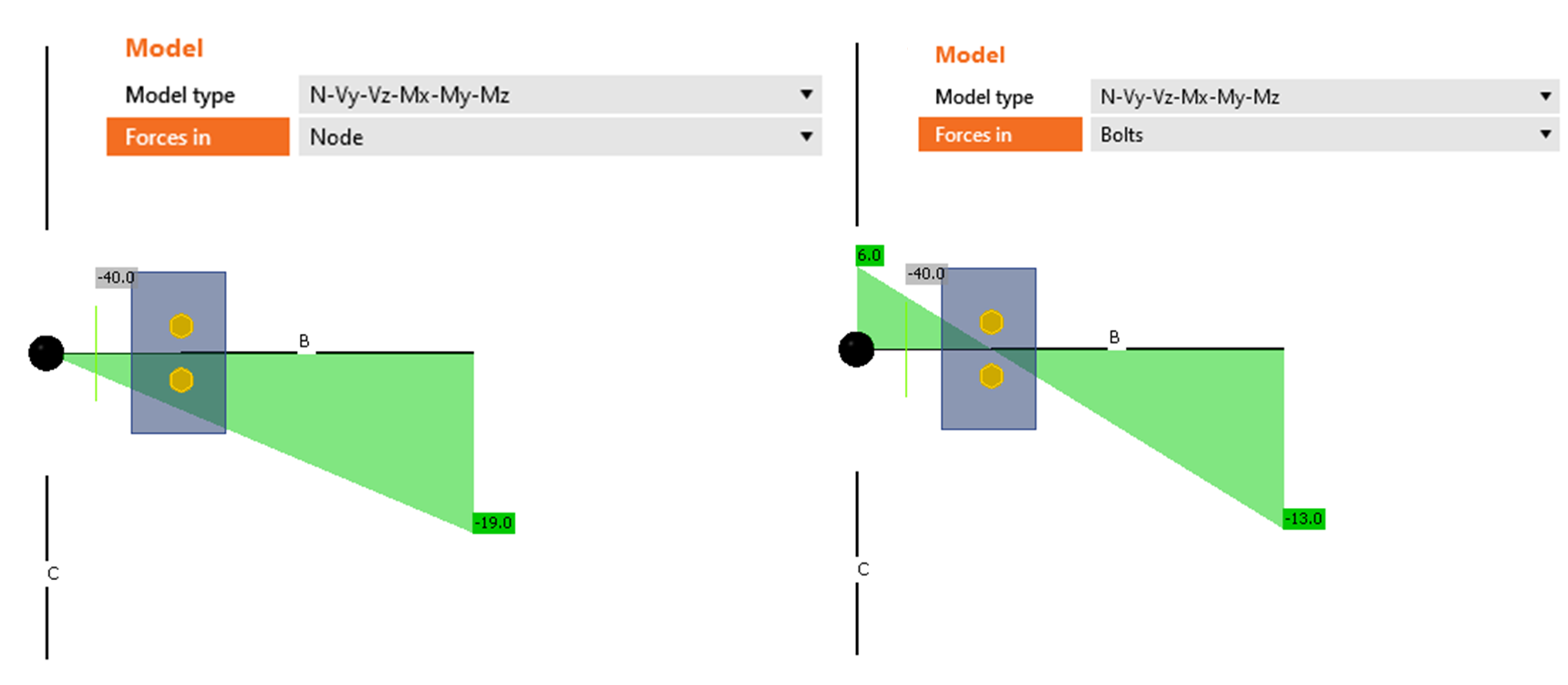
Left: Forces in Node Right: Forces in Bolts

In the situation on the left, there is a bending moment at the point of the hinge which causes the member to rotate upwards. This moment (originated from the shear force which linearly grows from the node point) induces the incorrect behavior of the horizontal member.

We can easily fix the setup by moving the shear force to act at the position of the hinge. In such a case (the right picture), the horizontal beam deflects as expected.

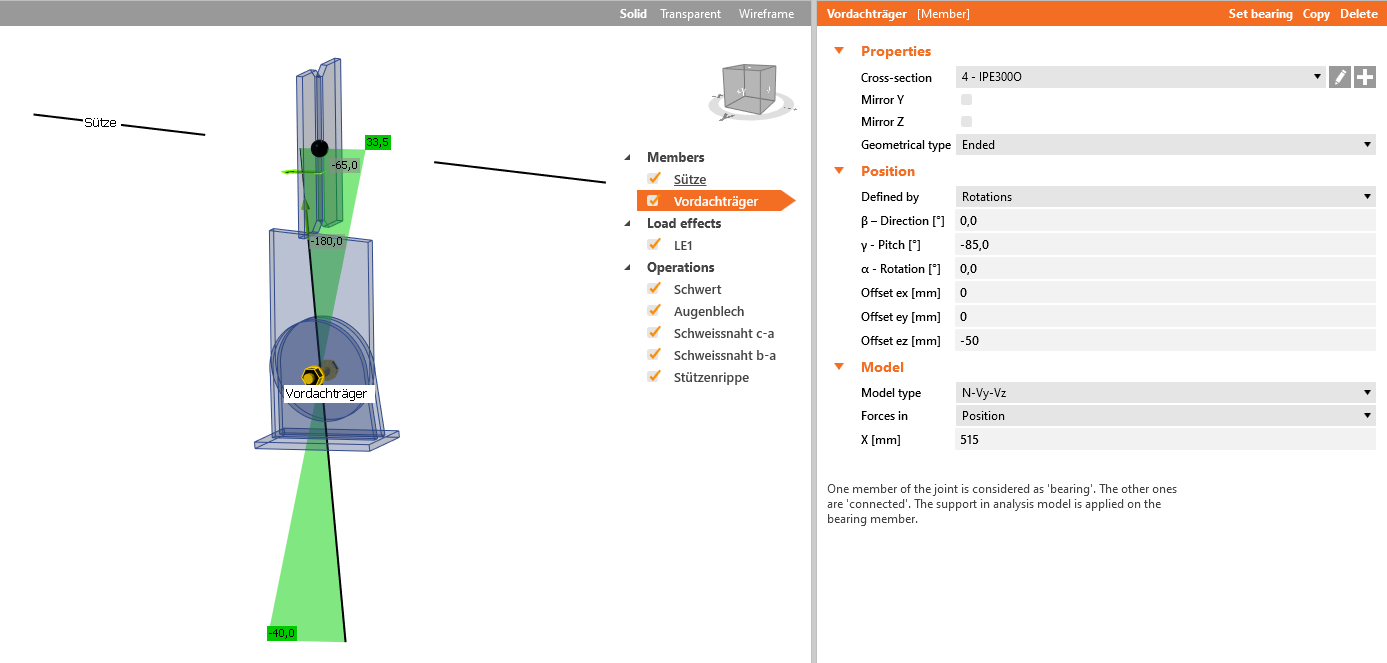
The third option is Forces in Position. For some operations, especially when creating a connection as an assembly of more basic operations (e.g. stiffening plate, cut, bolt grid), the function Forces in Bolts doesn't have any effect and there is no shift of the zero bending moment into the assumed hinge.

Therefore, the method Forces in Position must be chosen and the appropriate X distance must be input.

Since the 23.1 version, we have added an option to define the shear for a position at the member face. Read the corresponding article to learn about Shear force position input and visualization.

Hinged connections are often called shear connections. It must be emphasised that the position of the shear force can vary from one type of shear connection to another and it cannot be universally assumed that the zero bending moment is at the centre of gravity of the bolt group. Article When the shear connection transmits the bending moment discusses the differences between individual types of shear connections in more detail.

Webinar recording

See the recordings of our past webinars where the position of shear force is discussed.

The position of the nodal internal forces that we get from a structural model can be by eccentricities shifted from the origin. This effect underestimates the internal forces acting at the connection. Let's see how to change the position of internal forces directly in operation and avoid incorrect results.