Design of prestressed composite cross-section in RCS
Creating a new project
Initially, setting up a new project as a 1D staged/prestressed/composite member is necessary.
Design member
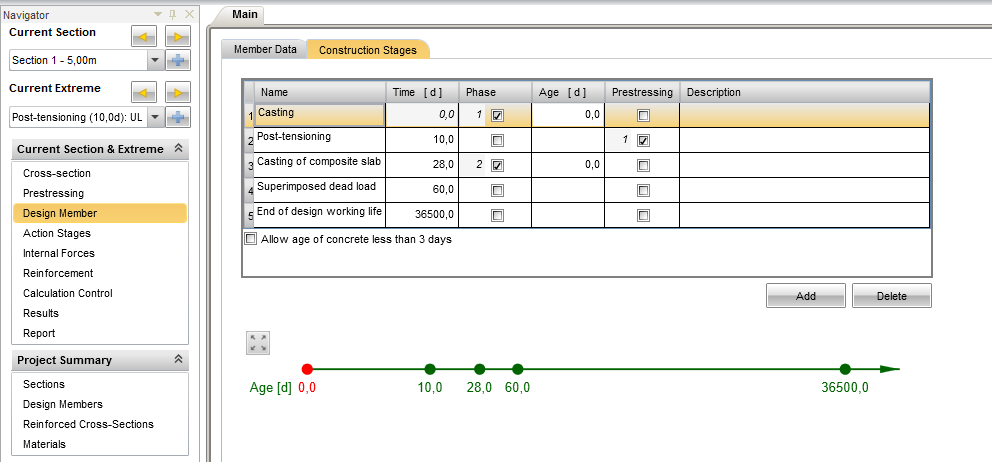
After defining the cross-section geometry and reinforcement layout, the timeline in the Construction Stages tab is defined. All important time points during the construction are defined (such as casting the first part of the cross-section of the precast beam, prestressing, casting the second part of the cross-section of the composite slab, superimposed dead load, and the time of the design working life). The defined construction stages are automatically propagated in the Action Stages tab.
Action stages
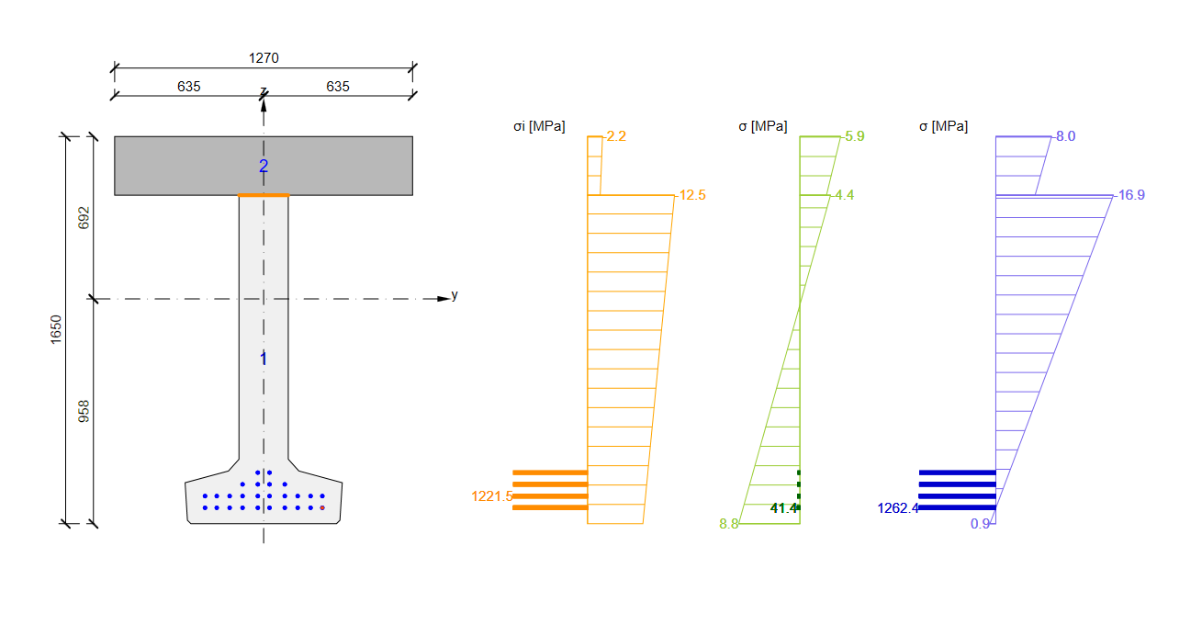
From the point of view of code-checking the composite cross-sections, the Action Stages tab is the most important. Defining the initial stress state of the cross-section calculated by Time-Dependent Analysis (TDA) is crucial since the discontinuity of stress (the plane of strain shift) at the interface between two different concretes can decide the failure mechanism at the limit state.
The initial state of the cross-section
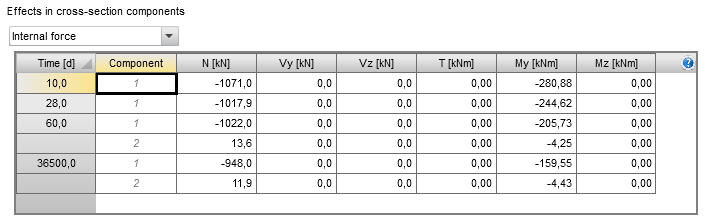
The initial state of the composite section is set in the table ”Effects in cross-section components”. Two options for defining the initial state can be chosen – internal forces and planes of strain. It is much easier to define internal forces obtained from TDA calculated by third-party software (Midas, SCIA, etc.)
The table ”Effects in cross-section components” contains the internal forces as a summation of:
- All permanent loads acting in the considered construction stage
- The total effect of prestressing (the primary and secondary effects of bonded and unbonded internal tendons, the primary and secondary effects of external tendons)
- Rheology (creep, shrinkage)
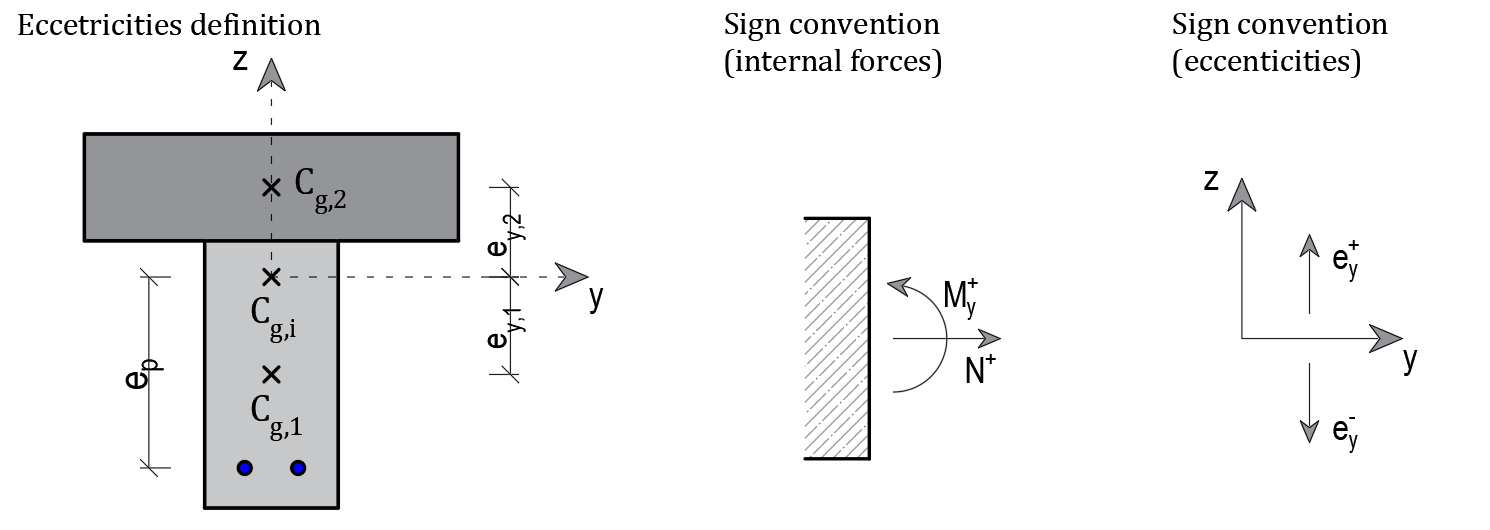
Most third-party software (Midas, SCIA, etc.) present the internal forces of each part of the composite cross-section related to the center of gravity of the considered cross-sectional part (for example, the bending moment in the precast beam is related to the center of gravity of the precast beam Cg,1). The RCS application relates the internal forces to the center of gravity of the actual cross-section (the button “Actual” in the ribbon) or the center of gravity of the final composite section Cg,i (the button “Entire” in the ribbon). Transformation of the internal forces obtained from third-party software to RCS can be performed according to the following formulas:
\[N_{i}^{T} = N_{i}\]
\[M_{i}^{T} = M_{i}-N_{i}\times e_{i}\]
NiT . . . . the normal force in the considered part of the composite section transformed to the center of gravity of the idealized final composite cross-section
MiT . . . . the bending moment in the considered part of the composite section transformed to the center of gravity of the idealized final composite cross-section
Ni . . . . the normal force in the considered part of the composite section related to the center of gravity of the considered cross-section part
Mi . . . . the bending moment in the considered part of the composite section related to the center of gravity of the considered cross-section part
Note: Keeping the sign convention presented in the figure below is important to recalculate the internal forces.
Cg,i . . . . the center of gravity of the idealized composite section (Ecm(28) is considered)
Cg,1 . . . . the center of gravity of part one – precast beam (light gray part)
Cg,2 . . . . the center of gravity of part two – composite slab (dark gray part)
ey,1 . . . . the distance from Cg,1 to Cg,i
ey,2 . . . . the distance from Cg,2 to Cg,i
ep . . . . the distance from the center of gravity of the prestressing reinforcement to Cg,i
The internal forces N1, My,1, N2 a My,2 are obtained for the composite structure modeled in third-party software and subjected in the vertical direction. For the correct input of the internal forces to the RCS app, a recalculation has to be performed as follows:
Part 1 (precast beam)
\[N_{1}^{T} = N_{1}\]
\[M_{y}^{T},_{1} = M_{y}^{T},_{1}-N_{1}\times e_{y},_{1}\]
N1T . . . . the normal force in the precast beam transformed to the center of gravity of the idealized final composite cross-section Cg,I (a negative value for compressive force)
My,1T . . . the bending moment in the precast beam transformed to the center of gravity of the idealized final composite cross-section Cg,i
N1 . . . . the normal force in the precast beam related to the center of gravity of the precast beam Cg,1
My,1 . . . the bending moment in the precast beam related to the center of gravity of the precast beam Cg,1
ey,1 . . . . the distance of the center of gravity of precast beam Cg,1 from the center of gravity of the idealized final composite cross-section Cg,i (in this case, the negative value of eccentricity is considered)
Part 2 (composite slab)
\[N_{2}^{T} = N_{2}\]
\[M_{y}^{T},_{2} = M_{y}^{T},_{2}-N_{2}\times e_{y},_{2}\]
N2T . . . . the normal force in the composite slab transformed to the center of gravity of the idealized final composite cross-section Cg,i
My,2T . . . the bending moment in the composite slab transformed to the center of gravity of the idealized final composite cross-section Cg,i
N2 . . . . the normal force in the composite slab related to the center of gravity of the composite slab Cg,2
My,2 . . . the bending moment in the composite slab related to the center of gravity of the composite slab Cg,2
ey,2 . . . . the distance of the center of gravity of composite slab Cg,2 from the center of gravity of the idealized final composite cross-section Cg,i (in this case, the positive value of eccentricity is considered)
Thanks to this transformation, the total internal forces in the composite cross-section can be determined.
\[N=N_{1}^{T}+N_{2}^{T}\]
\[M_{y}=M_{y}^{T},_{1}+M_{y}^{T},_{2}\]
Note: The transformation process of internal forces acting in a horizontal direction is the same as stated above.
Stress in reinforcement
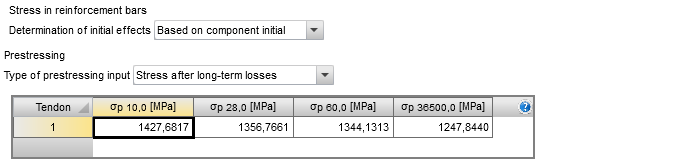
The next important step is determining the initial stress in rebars and prestressing tendons. The RCS application can calculate stress in rebars automatically, so it’s recommended to keep setting ”Based on a component initial”.
If the prestressing reinforcement is designed, the stress in each tendon for all existing construction stages must be defined (see Chapter 2). The RCS application allows the definition of the value of stress in tendons after long-term losses calculated by TDA (“Stress after long-term losses”) or the definition of estimated short- and long-term losses (“Estimation of prestressing losses”).
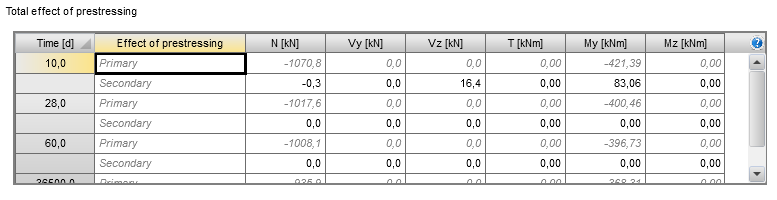
Total effects of prestressing
The RCS application recognizes two types of prestressing effects – the primary and secondary effects of prestressing. Both types are assumed to be acting on the final composite section. Prestressing effects are defined for each construction stage to capture long-term prestressing losses. The primary effects of prestressing are calculated automatically according to tendon properties (the position in a cross-section, the area of a tendon, and stress in a tendon in the considered construction stage). Internal forces due to primary prestressing at the time of 10 days are calculated as:
\[N_{p}^{P},_{10}=A_{p}\times \sigma_{p},_{10}\]
\[M_{p}^{P},_{10}=A_{p}\times \sigma_{p},_{10}\times e_{p}\]
Np,10P . . . the normal force in a cross-section due to the primary effects of bonded prestressing reinforcement in the considered time (10 days)
Mp,10P . . . the bending moment in a cross-section due to primary effects of bonded prestressing reinforcement in the considered time (10 days)
Ap . . . . the area of bonded prestressing reinforcement
σp,10 . . . the stress in prestressing reinforcement in the considered time (10 days)
ep . . . . the distance from the center of gravity of prestressing reinforcement to the center of gravity of the idealized final composite cross-section Cg,i
The user always defines the secondary effects of prestressing. Internal forces defined in the table consist of:
- The total effects of unbonded or external prestressing reinforcement (if the user defined this reinforcement type in the global calculation model).
- The total effects of unbonded or external prestressing reinforcement (if the user-defined this reinforcement type in the global calculation model)
The summation of primary and secondary effects defined in the table shown above are automatically copied to the table in the section “Internal forces”. It is necessary to define prestressing carefully and correctly to prevent incorrect results.
Internal forces
A few last steps hmust be performed for the correct code-checking of the composite cross-section. In “Section”, defining “Extremes” for each time the code-checking should be done is necessary. The defined times of extremes have to correspond to the times defined in “Construction stages” (chap. 2). Then correct values of internal forces for the calculation of the initial state of the cross-section will be taken from the tab ”Action stages”.
Other types of acting internal forces have to be defined in the “Internal forces” tab. Internal forces are defined for each extreme separately.
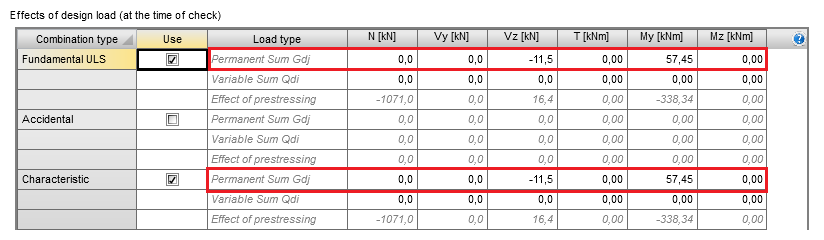
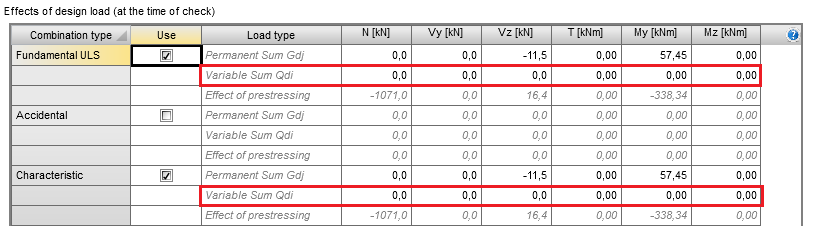
Permanent load
The rows called “Permanent Sum Gdj” serve as the input for the combination value of the permanent loads (including load factors) acting in the considered construction stage.
Permanent internal forces can be defined manually or imported from “Action stages” thanks to the commands in the ribbon. When importing ULS internal forces from “Action stages”, the load factor for the permanent load can be set by the user.
Import permanent internal forces from the “Action stages”, the following rules are applied:
- The combination value of internal forces for ULS checks is calculated as
Permanent Sum = (Initial effects of section – Total effects of prestressing) ·γGj,sup
- The combination values of internal forces for SLS checks are calculated as
Permanent Sum = Initial effects of section – Total effects of prestressing
Variable load
The resulting value of internal forces due to a variable load (including combination load factors) is defined manually by the user. These values are usually obtained from global structural analysis.
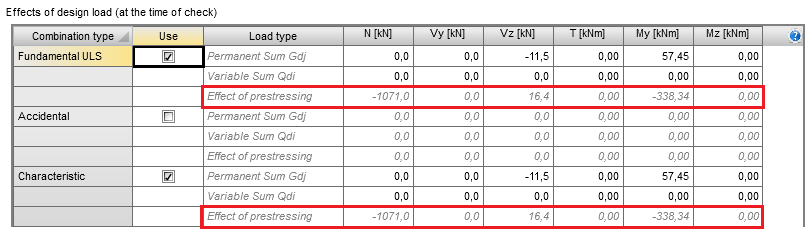
Effects of prestressing
The total effects of prestressing are automatically imported from the ”Action stages” tab as a summation of the primary and secondary effects of prestressing defined in the tab ”Total effects of prestressing” (chap. 3.3). These values cannot be edited by the user.