Code-check of anchors according to Australian standards
The forces in anchors including prying forces are determined by finite element analysis, but the resistances are checked using code provisions of AS 5216.
The check of anchors is provided according to AS 5216:2018. Although the code does not specifically provide some formulas for cast-in anchors, the formulas are the same as in SA TS 101:2015 where cast-in anchors are specifically mentioned. Cracked or uncracked concrete can be selected in Code setup. Cracked concrete is conservatively assumed as default. Concrete cone breakout check in tension and shear may be disregarded in Code setup, which means the force is assumed to be transferred via reinforcement. User is provided with the magnitude of this force. Due to the use of concrete cone breakout resistance in the formula in concrete pry-out failure check, this check is also disregarded.
Following checks of anchors loaded in tension are not provided and should be checked using information in relevant Technical Product Specification (testing according to AS 5216:2018: Appendix A):
- Pull-out failure of fastener (for post-installed mechanical anchors) – AS 5216:2018: 6.2.4,
- Combined pull-out and concrete cone failure (for post-installed bonded anchors) – AS 5216:2018: 6.2.5,
- Concrete splitting failure – AS 5216:2018: 6.2.6.
Concrete blow-out failure is provided only for anchors with washer plates.
Steel failure in tension
Steel failure in tension is checked according to Cl. 6.2.2:
\[ ϕ_{Ms} N_{tf} = ϕ_{Ms} A_s f_{uf} \]
where:
- \( ϕ_{Ms} = \frac{5 f_{yf}}{6 f_{uf}} \le 1/1.4 \) – capacity factor for steel failure in tension (Table 3.2.4)
- As – tensile stress area of a bolt as specified in AS 1275
- fuf – minimum tensile strength of the bolt as specified in AS 4100 – Table 9.3.1
Concrete cone failure
Concrete cone failure is checked according to Cl. 6.2.3 and is provided for the group of anchors (where applicable). The characteristic strength of the tensioned fasteners in a group or a single fastener is:
\[ ϕ_{Mc} N_{Rk,c} = ϕ_{Mc} N_{Rk,c}^0 \left ( \frac{A_{c,N}}{A^0_{c,N}} \right ) \psi_{s,N} \psi_{re,N} \psi_{ec,N} \psi_{M,N} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( N_{Rk,c}^0 = k_1 \sqrt{f'_c} h_{ef}^{1.5} \) – characteristic strength of a fastener, remote from the effects of adjacent fasteners or edges of the concrete member – Cl. 6.2.3.2
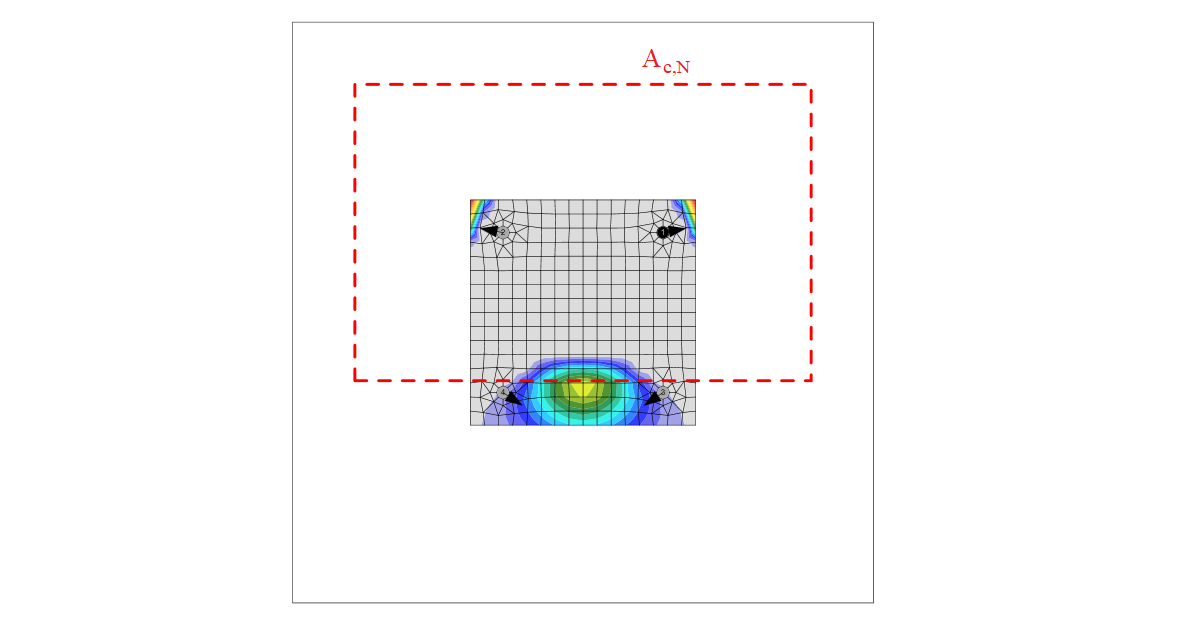
- Ac,N – actual projected area of the failure cone of the fastener that is limited by adjacent fasteners and edges of the concrete member – Cl. 6.2.3.3
- Ac,N0 = scr,N2 – reference projected area of a single fastener with an edge distance at least equal to 1.5 hef – Cl. 6.2.3.3
- \( \psi_{s,N} = 0.7 + 0.3 \frac{c}{c_{cr,N}} \le 1 \) – parameter related to the distribution of stresses in the concrete due to the proximity of the fastener to an edge of the concrete member – Cl. 6.2.3.4
- \( \psi_{re,N} = 0.5 + \frac{h_{ef}}{200} \le 1 \)– parameter accounting for the shell spalling effect – Cl. 6.2.3.5
- \( \psi_{ec,N} = \frac{1}{1+2 e_N / s_{cr,N}} \le 1 \) – parameter accounting for eccentricity of the resultant load in a fastener group – Cl. 6.2.3.6
- \( \psi_{M,N} = 2- \frac{2 z}{3 h_{ef}} \ge 1 \) – parameter accounting for the effect of a compression force between the fixture and concrete – Cl. 6.2.3.7; this parameter is equal to 1 if c < 1.5 hef or the ratio of the compressive force (including the compression due to bending) to the sum of tensile forces in anchors is smaller than 0.8
- \item k1 – parameter; for cast-in anchors (Anchor type – washer plates) k1 = kcr,N = 8.9 for cracked concrete and k1 = kucr,N = 12.7 for uncracked concrete; for post-installed anchors (Anchor type – straight) k1 = kcr,N = 7.7 for cracked concrete and k1 = kucr,N = 11.0 for uncracked concrete
- scr,N = 2 ccr,N = 3 hef – spacing of fasteners
- ccr,N = 1.5 hef – characteristic edge distance
- hef – effective embedment depth of the fastener, in case of narrow concrete member, Cl. 6.2.3.8 applies and\( h'_{ef} = \max \left ( \frac{c_{max}}{c_{cr,N}}h_{ef}; \, \frac{s_{max}}{s_{cr,N}}h_{ef} \right ) \)
- z – internal lever arm
- c – smallest edge distance
The concrete breakout cone area for group of anchors loaded by tension that create common concrete cone, Ac,N, is shown by red dashed line.
Pull-out failure
Pull-out failure is checked for cast-in headed fasteners (Anchor type – washer plate) according to SA TS 101:2015 – Cl. 6.2.3:
\[ ϕ_{Mc} N_{Rk,p} = k_1 A_h f'_c \]
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- k1 –parameter relating to the state of the concrete; for cracked concrete k1 = 8.0, for uncracked concrete k1 = 11.2
- Ah – area of the load-bearing head of the fastener; for circular washer plate \( A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right \)$, for rectangular washer plate \( A_h = a_{wp}^2 - \frac{\pi}{4} d^2 \)
- dh ≤ 6 th + d – diameter of head of fastener
- th – thickness of the head of the headed fastener
- d – diameter of the shank of the fastener
- awp – length of the edge of the rectangle washer plate
- f'c – characteristic compressive strength of concrete
The pull-out failure for other than cast-in headed anchors is not calculated and the resistance should be guaranteed by a manufacturer or determined by testing and assessment in accordance with Appendix A.
Neither resistance to splitting failure during installation (Cl. 6.2.6.1) nor due to loading (Cl. 6.2.6.2) is provided and should be guaranteed by a manufacturer or determined by testing and assessment in accordance with Appendix A.
Blow-out failure
Blow-out failure is checked for headed anchors (Anchor type – washer) with edge distance c ≤ 0.5 hef according to Cl. 6.2.7. Anchors are treated as a group if their spacing near the edge is s ≤ 4 c1. Undercut anchors can be checked the same way but the value of Ah is unknown in the software. The blow-out failure of undercut anchors can be determined by selecting washer plate with the corresponding dimension.
\[ ϕ_{Mc} N_{Rk,cb} = ϕ_{Mc} N_{Rk,cb}^0 \frac{A_{c,Nb}}{A_{c,Nb}^0} \psi_{s,Nb} \psi_{g,Nb} \psi_{ec,Nb} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( N_{Rk,cb}^0 = k_5 c_1 \sqrt{A_h} \sqrt{f'_c} \) – characteristic strength of a single fastener remote from the effects of adjacent fasteners and edges of the concrete member – Cl. 6.2.7.2
- Ac,Nb – actual projected area for the fastener that is limited by the edges of the concrete member (c2 ≤ 2 c1, the presence of adjacent fasteners (s ≤ 4 c1) or the member thickness – Cl. 6.2.7.3
- Ac,Nb0 = (4 c1)2 – reference projected area of a single fastener with an edge distance equal to c1 – Cl. 6.2.7.3
- \( \psi_{s,Nb} = 0.7+0.3 \frac{c_2}{2 c_1} \le 1 \) – parameter accounting for the disturbance of stresses in the concrete due to the close proximity of the fastener to a corner of the concrete member – Cl. 6.2.7.4
- \( \psi_{g,Nb} = \sqrt{n} + (1-\sqrt{n}) \frac{s_2}{4c_1} \ge 1 \) – parameter accounting for a group effect – Cl. 6.2.7.5
- \( \psi_{ec,Nb} = \frac{1}{1+2 e_N / s_{cr,Nb}} \le 1 \) – parameter accounting for eccentricity of loading on a fastener group – Cl. 6.2.7.6
- k5 – parameter related to the state of the concrete; for cracked concrete k5 = 8.7, for uncracked concrete k5 = 12.2
- c1 – edge distance of fastener in direction 1 towards the closest edge
- c2 – edge distance of fastener perpendicular to direction 1 that is the smallest edge distance in a narrow member with multiple edge distances
- Ah – area of the load-bearing head of the fastener; for circular washer plate \( A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right \), for rectangular washer plate \( A_h = a_{wp}^2 - \frac{\pi}{4} d^2 \)
- f'c – characteristic compressive strength of concrete
- n – number of fasteners in a row parallel to the edge of the concrete member
- s2 – spacing of fasteners in a group perpendicular to direction 1
- scr,Nb = 4 c1 – spacing that is required for a fastener to develop its characteristic tensile strength against blow-out failure
According to Cl. 6.2.8, the supplementary reinforcement may be used to transfer forces causing concrete blow-out failure. Such reinforcement should be designed in accordance with AS 3600.
Steel failure in shear
Steel failure in shear is determined according to Cl. 7.2.2. It is assumed that the anchor is made of threaded rod with the same material properties as bolts.
Shear force without lever arm
Shear force without lever arm is assumed if stand-off – direct is selected. It is assumed that fasteners are from ductile steel and factor k7 = 1. Each fastener is checked separately. The resistance is determined according to AS 5216 – Cl. 7.2.2.2 and AS 4100 – Cl. 9.2.2.1:
\[ ϕ_{Ms} V_{Rk,s} = ϕ_{Ms} 0.62 f_{uf} A \]
where:
- \( ϕ_{Ms} = f_{yf} / f_{uf} \le 0.8 \) when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- fuf – minimum tensile strength of the bolt as specified in AS 4100 Table 9.2.1
- A – area of a bolt equal either to Ac or Ao which are minor diameter area of the bolt as defined in AS 1275 or nominal plain shank area of the bolt, respectively
For fasteners with hef / d < 5 in concrete having f’c < 20 MPa, VRk,s is multiplied by a factor equal to 0.8.
Shear force with lever arm
Steel shear strength with lever arm is calculated according to Cl. 7.2.2.3:
\[ ϕ_{Ms} V_{Rk,s,M} = ϕ_{Ms} \frac{\alpha_M M_{Rk,s}}{l_a} \]
where:
- \( ϕ_{Ms} = f_{yf} / f_{uf} \le 0.8 \) when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- αM = 2 – parameter accounting for the degree of restraint, fixture is assumed to be prevented from rotating – Cl. 4.2.2.4
- \( M_{Rk,s} = M_{Rk,s}^0 \left ( 1- \frac{N^*}{ϕ_{Ms} N_{Rk,s}} \right ) \) – characteristic flexural strength of the fastener influenced by the axial load
- la = a3 + e1 – length of the lever arm
- a3 = 0.5 d – distance between the assumed point of restraint of the fastener loaded in shear and the surface of the concrete
- e1 = tg + tfix / 2 – eccentricity of the applied shear load relative to the concrete surface, neglecting the thickness of a levelling grout or mortar
- tg – thickness of grout layer
- tfix – thickness of base plate
- d – nominal diameter of the fastener
- N* – design tension load
- ϕMs NRk,s – tensile strength of a fastener to steel failure
- MRk,s0 = 1.2 Wel fuf – characteristic flexural strength of the fastener – ETAG 001 – Annex C
- Wel = π d3 / 32 – elastic section modulus of the fastener, the diameter reduced by threads, \( d_s = \sqrt{\frac{4 A_s}{\pi}} \), is used instead of nominal diameter, d, if Shear plane in thread is selected
Concrete edge failure
Concrete edge failure is checked according to Cl. 7.2.3. If concrete cones of fasteners intersect, they are checked as a group. The edges in the direction of the shear load are checked. All load at a base plate is presumed to be transferred by a fastener near the checked edge.
\[ ϕ_{Mc} V_{Rk,c} = ϕ_{Mc} V_{Rk,c}^0 \frac{A_{c,V}}{A_{c,V}^0} \psi_{s,V} \psi_{h,V} \psi_{ec,V} \psi_{\alpha,V} \psi_{re,V} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- \( V_{Rk,c}^0 = k_9 d^{\alpha} l_f^{\beta} \sqrt{f'_c} c_1^{1.5} \) – initial value of the characteristic shear strength of the fastener – Cl. 7.2.3.2
- Ac,V – actual area of idealised concrete break-out body – Cl. 7.2.3.3
- Ac,V0 = 4.5 c12 – reference projected area of failure cone – Cl. 7.2.3.3
- \( psi_{s,V} = 0.7 + 0.3 \frac{c_2}{1.5 c_1} \le 1 \) – parameter accounting for the disturbance to the distribution of stresses in the concrete member – Cl. 7.2.3.4
- \( \psi_{h,V} = \left ( \frac{1.5 c_1}{h} \right ) ^{0.5} \ge 1 \) – parameter accounting for the influence of member thickness – Cl. 7.2.3.5
- \( \psi_{ec,V} = \frac{1}{1+2 e_V / (3c_1)} \le 1 \) – parameter accounting for the eccentricity of the resultant load in a fastener group – Cl. 7.2.3.6
- \( \psi_{\alpha,V} = \sqrt{\frac{1}{(\cos \alpha_V)^2 + (0.5 \sin \alpha_V)^2}} \ge 1 \) – parameter accounting for the angle of the applied load – Cl. 7.2.3.7
- ψre,V = 1 – parameter accounting for the shell spalling effect – Cl. 7.2.3.8, no edge reinforcement or stirrups are assumed
- k9 – parameter accounting for the state of the concrete; for cracked concrete k9 = 1.7, for uncracked concrete k9 = 2.4
- d – nominal diameter of the fastener
- \( \alpha = 0.1 \left ( \frac{l_f}{c_1} \right ) ^{0.5} \)
- \( \beta = 0.1 \left ( \frac{d}{c_1} \right ) ^{0.2} \)
- lf = hef ≤ 12 d where d ≤ 24 mm; lf = hef ≤ max (8 d, 300 mm) where d > 24 mm – parameter related to the length of the fastener
- f'c – characteristic compressive cylinder strength of concrete at 28 days
- c1 – edge distance of fastener to the investigated edge; according to Cl. 7.2.3.9, for a narrow member, c2,max < 1.5 c1 that is also deemed to be thin, h < 1.5 c1, c'1 is used in previous equations instead of c1; the reduced c'1 = max (c2,max / 1.5, h/ 1.5, sc,max / 3)
- c2 – the smaller edge distance of fastener in the direction perpendicular to the investigated edge
- h – concrete member thickness
- eV – eccentricity of the resultant shear force acting on a group of fasteners relative to the centre of gravity of the fasteners loaded in shear
- αV – angle between the applied load to the fastener or fastener group and the direction perpendicular to the free edge under consideration, 0° < αV < 90°
- hef – effective embedment depth of the fastener
Concrete pry-out failure
Concrete pry-out failure is checked according to Cl. 7.2.4. All anchors at one base plate are assumed to be loaded in shear and the concrete breakout resistance, NRk,c, used in the calculation, is calculated with the assumptions of all anchors loaded in tension without any eccentricity. No supplementary reinforcement is assumed.
\[ ϕ_{Mc} V_{Rk,cp} = ϕ_{Mc} k_8 N_{Rk,c} \]
where:
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
- k8 – parameter published in the Report of Assessment, according to ETAG 001 – Annex C, for hef < 60 mm, k8 = 1 and for hef ≥ 60 mm, k8 = 2
- NRk,c – characteristic concrete cone strength for a single fastener or fastener in a group
Combined tension and shear loading
The resistance of a fastener loaded by combined tension and shear is determined according to Chapter 8.
Steel failure
An assessment of the performance under combined tension and shear loading of the fastener is based on AS 4100:
\[ \left ( \frac{N^*}{ϕ_{Ms} N_{Rk,s}} \right ) ^2 + \left ( \frac{V^*}{ϕ_{Ms} V_{Rk,s}} \right ) ^2 \le 1.0 \]
Concrete failure
Failure modes other than steel are checked according to Cl. 8.2.1:
\[ \left ( \frac{N^*}{ϕ_{Mc} N_{Rk,i}} \right ) ^{1.5} + \left ( \frac{V^*}{ϕ_{Mc} V_{Rk,i}} \right ) ^{1.5} \le 1.0 \]
where:
- N* – design tension force applied to a single fastener or group
- V* – design shear force applied to a single fastener or group
- NRk,i – characteristic tensile strength of fastener or group to failure mode ‘i’
- VRk,i – characteristic shear strength of fastener or group to failure mode ‘i’
- \( ϕ_{Ms} = \frac{5 f_{yf}}{6 f_{uf}} \) – capacity factor for steel failure in tension (Table 3.2.4)
- ϕMs = fyf / fuf ≤ 0.8 when fuf ≤ 800 MPa and fyf / fuf ≤ 0.8; ϕMs = 2/3 otherwise – capacity factor for steel failure in shear (Table 3.2.4)
- ϕMc – capacity factor for anchor failure modes connected to concrete editable in code setup; recommended value is 1/1.5 (Table 3.2.4)
Stand-off anchors
Anchors with stand-off are designed as beam member according to AS 4100 with capacity factors of bolts. The assumed length of the member is the sum of the height of gap, half of nominal diameter thickness and half of the base plate thickness. Stand-off anchors are usually checked as a construction stage before grouting.
Bending capacity
Bending capacity is determined according to AS 4100, Cl. 5.1.
M* ≤ ϕ Ms
where:
- M* – bending moment acting on anchor determined by finite element method
- ϕ = 0.8 – capacity factor for bolts
- Ms = fy Ze – section moment capacity for bending
- fy – anchor yield strength
- Ze = min {S, 1.5 · Z} – effective section modulus – Cl. 5.2.3
- \( S = \frac{d^3}{6} \) – plastic section modulus; if Shear plane in thread is selected, nominal diameter d is replaced by diameter reduced by threads, ds
- \( Z = \frac{1}{32} \pi d^3 \) – elastic section modulus; if Shear plane in thread is selected, nominal diameter d is replaced by diameter reduced by threads, ds
Shear capacity
Shear capacity is determined according to AS 4100, Cl. 5.11.
V* ≤ ϕ Vw
where:
- V* – design shear force
- ϕ = 0.8 – capacity factor for bolts
- Vw = 0.6 fy Aw – nominal shear yield capacity – Cl. 5.11.4
- fy – anchor yield strength
- Aw = 0.844 As – shear area
- As – tensile stress area of a bolt as defined in AS 1275
Axial compression capacity
Axial compression capacity is determined according to AS 4100, Cl. 6. Buckling is taken into account according to Cl. 6.3:
N* ≤ ϕ Nc
where:
- N* – design compressive force
- ϕ = 0.8 – capacity factor for bolts
- Nc = αc Ns ≤ Ns – nominal member capacity – Cl. 6.3.3
- Ns = kf As fy – nominal section capacity – Cl. 6.2
- fy – anchor yield strength
- le = ke l – effective length – Cl. 6.3.2
- ke = 2 – member effective length factor, it is assumed conservatively that the anchor is fixed and the bottom and pinned at the top as sway member
- l = lgap + d / 2 + tp / 2 – assumed length of the member
- lgap – gap height
- d – nominal bolt diameter
- tp – base plate thickness
- \( \alpha_c = \xi \left \{ 1 - \sqrt{1- \left ( \frac{90}{\xi \lambda} \right )^2 } \right \} \) – compression member slenderness reduction factor – Cl. 6.3.3
- \( \xi = \frac{\left( \frac{\lambda}{90} \right)^2 + 1 + \eta}{2 \left( \frac{\lambda}{90} \right)^2} \) – compression member factor – Cl. 6.3.3
- \( \lambda = \lambda_n + \alpha_a \alpha_b \) – slenderness ratio – Cl. 6.3.3
- \( \eta = 0.00326 (\lambda-13.5) \) – compression member imperfection factor – Cl. 6.3.3
- \( \lambda_n = \frac{l_e}{r} \sqrt{k_f} \sqrt{\frac{f_y}{250}} \) – modified compression member slenderness – Cl. 6.3.3
- kf = 1 – form factor – Cl. 6.2.2
- \( r = \sqrt{\frac{I_s}{A_s}} \) – radius of gyration
- \( I_s = \frac{1}{64} \pi d_s^4 \) – moment of inertia
- As – tensile stress area of a bolt as defined in AS 1275
- \( d_s = \sqrt{\frac{4 A_s}{\pi}} \) – diameter reduced by threads
- \( \alpha_a = \frac{2100 (\lambda_n - 13.5)}{\lambda_n^2 - 15.3 \lambda_n + 2050} \) – compression member factor – Cl. 6.3.3
- αb = 0.5 – compression member section constant - Table 6.3.3
Axial tension capacity
Axial tension capacity is determined according to AS 4100, Cl. 7:
N* ≤ ϕ Nt
where:
- N* – design tensile force
- ϕ = 0.8 – capacity factor for bolts
- Nt = As fy – nominal section capacity of a bolt in tension – Cl. 7.2
- As – tensile stress area of a bolt as specified in AS 1275
- fy – anchor yield strength
Interaction of loading
If an anchor with stand-off is loaded by shear load and the compressive force, check of interaction of loading is performed:
\[ \frac{N^*}{\phi N_c} + \frac{M^*}{\phi M_s} \le 1 \]
where:
- N* – design compressive force
- ϕ = 0.8 – capacity factor for bolts
- Nc – compressive resistance
- M* – design bending moment due to shear on a lever arm
- Ms – bending resistance
Additionally, the checks of steel shear failure and concrete shear failures (concrete edge failure, concrete pryout failure) are performed.
If an anchor with stand-off is loaded by shear load and tensile force, check of interaction of loading is performed:
\[ \frac{N_{tf}^*}{\phi N_{t}} + \frac{M^*}{\phi M_s} \le 1 \]
where:
- N*tf – design tensile force
- ϕ = 0.8 – capacity factor for bolts
- Nt – tensile resistance
- M* – design bending moment due to shear on a lever arm
- Ms – bending resistance
Additionally, the checks of steel shear failure and concrete failures due to tension and shear are performed.