Accurate calculation of the shear resistance of slabs
The calculation of the resulting shear force was calculated in the past only according to the following formula:
\[{{v}_{d,max~}}=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}\]
Then, the maximal force was applied to all analyzed angles. In addition, the contribution of normal forces was taken into account only in the main axes directions and it could happen that the shear check was too conservative.
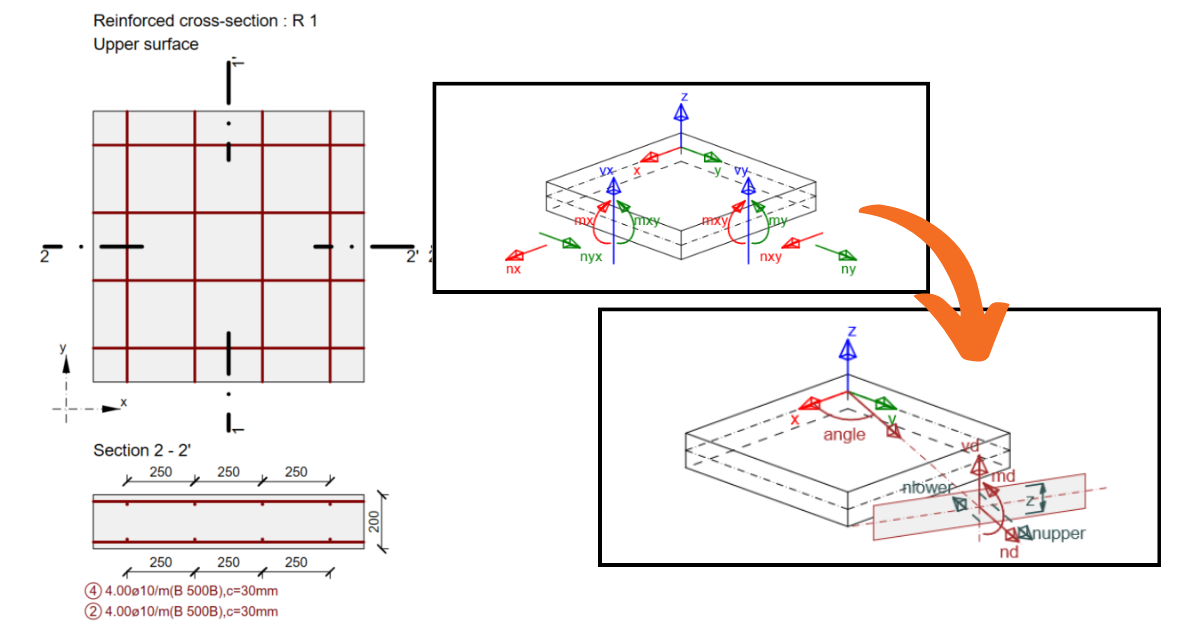
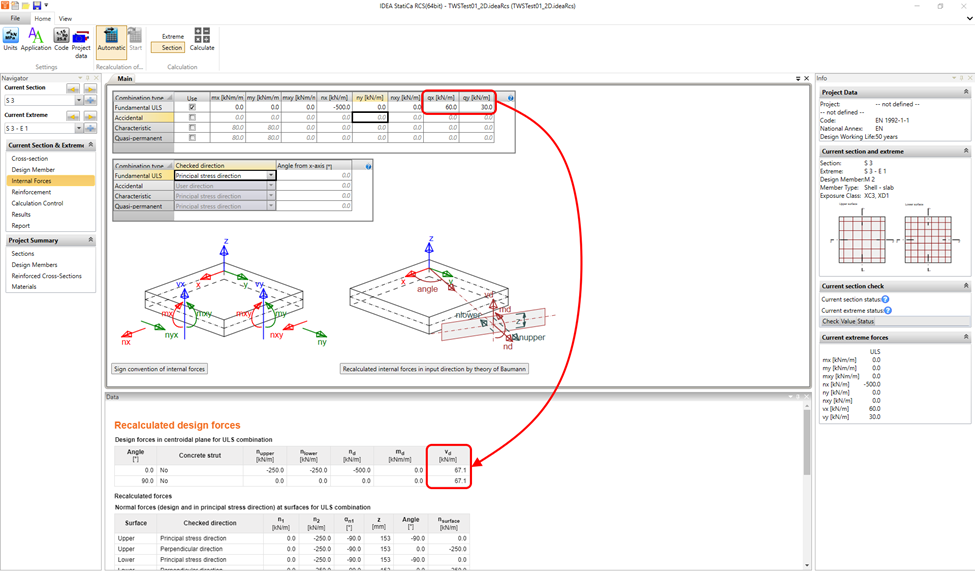
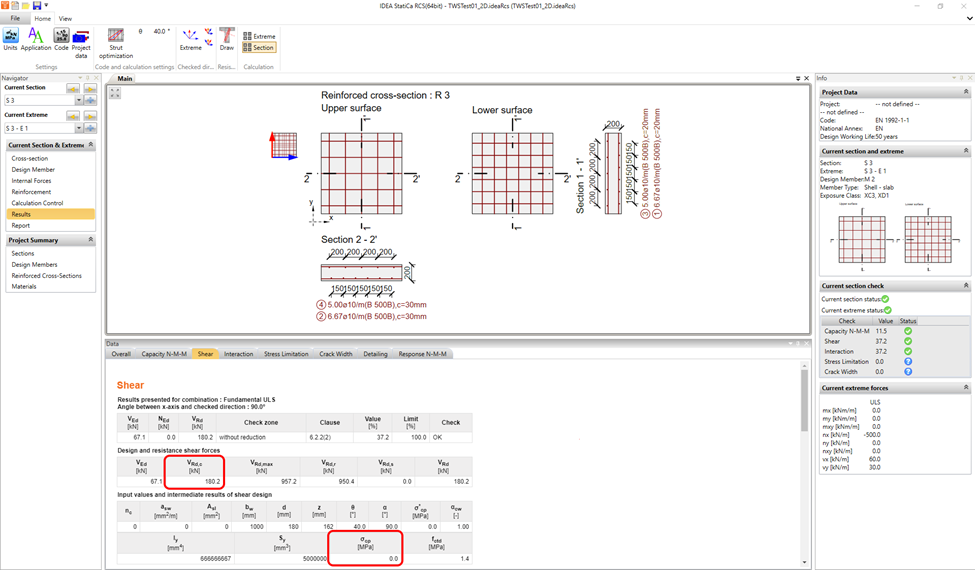
An illustrative example is shown in the figure above. A vertical uniform load qx and qy and a normal force in the x-axis direction only are specified. When recalculating the design forces, the maximum design shear force of 67.1 kN/m was considered for both principal directions, but the corresponding normal force for the 90° angle was zero. Since according to EN 1992-1-1, 6.2.2 (1) the normal compressive force affects the design shear capacity VRd,c through the value of σcp, the size of the shear capacity for an angle of 90° was based conservatively in this case.
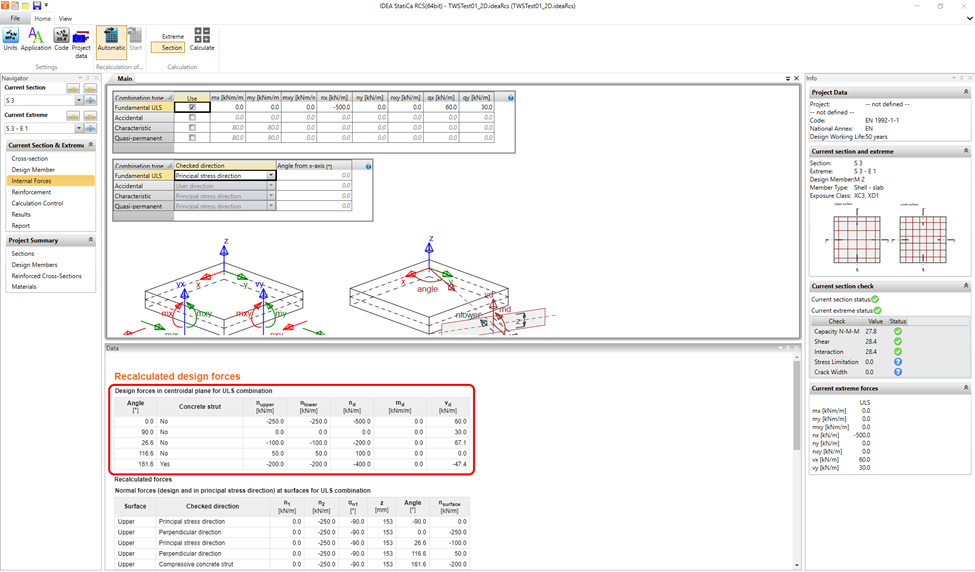
Newly in IDEA StatiCa RCS, there are the angle corresponding to the direction of the resultant shear force (26.6°), the angle perpendicular to the direction of the resultant shear force(116.6)°, and the angle of the in-plane concrete strut. A corresponding shear force and other internal forces are assigned to these angles.
A critical shear check's angle is now different (26.6°). The results are more accurate with proper VRd,c, respectively σcp values.
This method accurately determines the direction of shear force and conducts code checks accordingly, aligning with the corresponding internal forces. You can find more information on how the internal forces are recalculated in the Theoretical Background for RCS - 2D sections.
If you are interested in designing concrete slabs and would like to know more about Baumman theory implemented in IDEA StatiCa RCS, try our webinar: Baumann's method for design of concrete shells in practice.
Released in IDEA StatiCa patch 23.1.2.