Verification of IDEA StatiCa calculations for steel connection design (AISC)
Authors:
- Baris Kasapoglu, Ph.D. student (Department of Civil, Environmental and Geodetic Engineering)
- Rafael Arthur Giorjao, Ph.D. (Department of Materials Science and Engineering)
- Ali Nassiri, Ph.D. (Department of Integrated Systems Engineering)
- Halil Sezen, Ph.D. (Department of Civil, Environmental and Geodetic Engineering)
June 2021
Introduction
In the field of structural and civil engineering, understanding the structural behavior and integrity of the building is critical to ensure the safety of its occupants. However, it is a challenge to analyze and determine the behavior of a complex structure when it is subjected to a variety of loading conditions using conventional analytical methods. Therefore, Finite Element Analysis (FEA) is a valuable tool for numerically modeling physical structures that are too complex for analytical solutions. The overarching objective of this report is to evaluate the FEA results obtained from the IDEA StatiCa software package for three groups of common steel connections used in the United States (i.e., simple, semi-rigid, and rigid connections), and compare them with available experimental data and the results calculated from another FEA software, ABAQUS. The beam-column joint response obtained from the IDEA StatiCa software is then compared with the design calculations performed following the requirements of the AISC 360, Specification for Structural Steel Building (2016), and AISC Steel Construction Manual (2017) codes.
This report includes four chapters. In Chapters 1–3, an experimentally validated connection design was chosen from the literature for each connection type as a base model. The code design checks and calculations were performed according to the U.S. building codes for each base model and its ten variations. Then, the results were compared with the IDEA StatiCa predictions. Additionally, the FEA results from the IDEA StatiCa were compared with those from ABAQUS. All of the required steps and details of all geometric and design checks according to the AISC design codes are included in appendices. The last chapter contains the overall evaluation of the IDEA StatiCa software in terms of its accuracy and compatibility with the requirements of the U.S. building codes for the steel connections.
1 SIMPLE CONNECTIONS
In this study, the design strength capacities of ten pin connection specimens were calculated following the requirements of the AISC 360 (2016) and AISC Construction Manual (2017). Four test specimens were selected from the experimental study performed by McMullin and Astaneh (1988) in the Department of Civil Engineering at the University of California, Berkeley. Six additional models were developed for verification purposes by modifying the parameters based on the available test specimens. Then, the baseline model was analyzed using ABAQUS (2020) and IDEA StatiCa (Version 20.1.3471.1) and the results were compared.
Experimental Study
Seven full-scale steel beam-column connection specimens were tested, and results were presented in McMullin and Astaneh (1988). Each connection specimen was bolted to the beam and welded to the column with double angle sections. The main goal of these tests is to apply only shear force in the connection with very small bending or moment. To achieve this objective, the actuator near the connection applies the shear force. The actuator near the tip of the cantilever aims to keep the beam horizontal and limit the rotation (bending) of the connection.
Diagram of the instrumentation used during the experiment (McMullin and Astaneh, 1988)
Code Design Calculations and Comparisons
The design strength capacities (\(\phi\)Rn) of the connections were calculated following the requirements of AISC Specification for Structural Steel Buildings (AISC 360, 2016) and AISC Steel Construction Manual (AISC Manual, 2017). The nominal strength, Rn, and the corresponding resistance factor, \(\phi\), for each connection design limit state for load and resistance factored design (LRFD) are provided in Chapter J of AISC 360. The following 13 design checks were performed according to the LRFD design equations included in AISC 360 or AISC Manual.
- Bolt Shear Check (Eq. J3-1, AISC 360-16)
- Bolt Tensile Check (Eq. J3-1, AISC 360-16)
- Bolt Bearing on Beam (AISC 360-16, Eq. J3-6a)
- Bolt Tearout on Beam (AISC 360-16, Eq. J3-6c)
- Bolt Bearing on Angles (AISC 360-16, Eq. J3-6a)
- Bolt Tearout on Angles (AISC 360-16, Eq. J3-6c)
- Shear Rupture on Angles (Beam Side) (AISC 360-16, Eq. J4-4)
- Block Shear on Angles (Beam Side) (AISC 360-16, Eq. J4-5)
- Shear Yielding on Angles (AISC 360-16, Eq. J4-3)
- Shear Yielding on Beam (AISC 360-16, Eq. J4-3)
- Welds Rupture on Angles (Support Side) (Page 9-5, AISC Manual)
- Weld Capacity (Page 10–11, AISC Manual)
- Weld Capacity (no eccentricity) (AISC 360-16, Eq. J4-2)
IDEA StatiCa Analysis
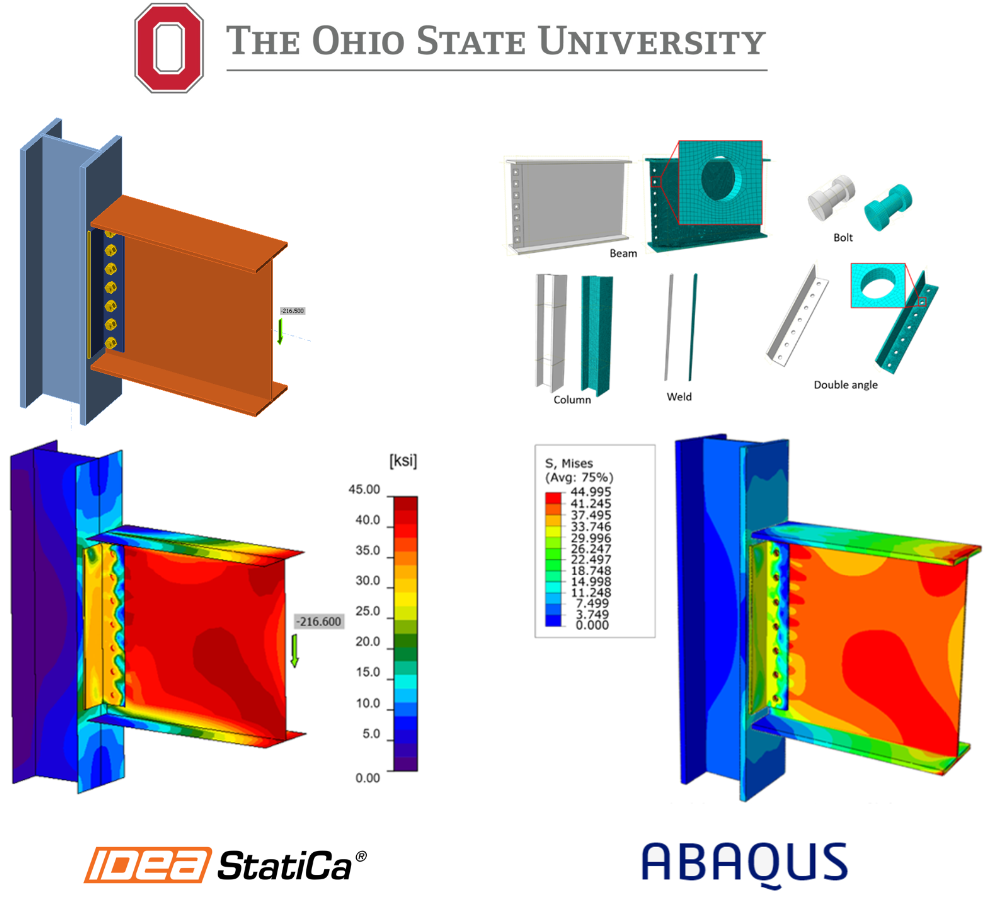
IDEA StatiCa checks four different failure scenarios of this steel connection type: (1) plate failure, (2) bolt failure, (3) weld failure, and (4) buckling. The selected four test specimens (Table 1.4) and six additional models (Table 1.6) were modeled in IDEA StatiCa and analyzed under a shear force, as shown in Figure 1.9. In the software, the location of the shear force can be arbitrarily selected. Two shear force locations were investigated: (1) in bolts, and (2) at the column face.
Comparison of shear capacities: Four tested specimens
| Strength Capacities | Test No. 4 | Test No. 5 | Test No. 6 | Test No. 9 |
| Strength by IDEA StatiCa - force applied on bolts (kips) | 130.2 | 73.4 | 31.3 | 61.3 |
| Strength by AISC Manual - force applied on bolts (kips) | 186.8 | 114.6 | 48.1 | 126.6 |
| Strength by IDEA StatiCa - force applied on welding (kips) | 216.6 | 145.4 | 74.8 | 168.0 |
| Strength by AISC 360-16 Eq. J2.4 - force applied on welding (kips) | 228.3 | 161.5 | 94.7 | 201.9 |
| Ultimate Shear Measured During Experiments (kips) | 230 | 205 | 117 | 192 |
Comparison of shear capacities: six additional models
| Strength Capacities | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
| Strength by IDEA StatiCa - force applied on bolts (kips) | 127.3 | 200.1 | 129.1 | 130.2 | 132.3 | 127.9 |
| Strength by AISC Manual - force applied on bolts (kips) | 233.5 | 186.8 | 139.9 | 186.8 | 186.8 | 214.4 |
| Strength by IDEA StatiCa - force applied on welding (kips) | 229.0 | 226.7 | 136.0 | 216.5 | 213.3 | 234.1 |
| Strength by AISC 360-16 Eq. J2.4 - force applied on welding (kips) | 285.4 | 228.1 | 139.9 | 228.1 | 228.1 | 285.4 |
Summary and Comparison of Results
Two different weld capacities were calculated for each test specimen following the AISC LRFD design requirements. For the same four test specimens, two different weld capacities were calculated from the IDEA StatiCa models by applying the shear force at different locations. In all loading scenarios, it was found that the weakest component of the connections was welding. The controlling or smallest calculated strengths corresponding to the weld capacities are presented and compared with the ultimate welding shear capacity measured during the experiment.
Weld capacities of the test specimens were computed in two different ways by following the AISC LRFD code requirements (AISC 360-16 and AISC Manual, 2017). For Test No. 4, if Equation J2.4 in AISC 360-16 is followed, the weld design capacity of the specimen is calculated as 228.3 kips. In this solution, no eccentricity is taken into account. To compare this approach with the IDEA StatiCa analysis, the vertical shear force was applied on the welding (parallel to the weld line) and the welding capacity of this specimen was calculated as 216.6 kips, which is very close to the one calculated from Equation J2.4 in AISC 360-16 (228.3 kips).
When the shear force is applied on the bolts (external vertical force parallel to the bolt line) in the IDEA StatiCa model, the connection capacity was computed as 130.2 kips. If the welding capacity is calculated by following the LRFD weld strength equation (Page 10-11 of AISC Construction Manual, 2017), which considers the eccentricity of the loading on the support side, the welding capacity of the specimen is calculated as 186.8 kips. However, conservatively this AISC LRFD equation does not account for the eccentricity resulting from the gap between the bolts and welding. It is believed that this assumption is the reason for the difference between the results calculated from IDEA StatiCa and LRFD strength equation in the AISC Manual (2017).
Comparison of IDEA StatiCa and ABAQUS Results
In general, there was good agreement between the results of two software packages. In case 1, in which load was applied on the centroid of the bolt group, more deformation was observed on the double angles in the ABAQUS model. Also, the maximum predicted stress on the beam, column, and weld lines was slightly higher in the ABAQUS model. In addition, slightly different stress distribution was observed on the beam in the ABAQUS model. While applying the load on the bolt group is not common in traditional finite element software, such discrepancy could be associated with different contact formulations or element types (i.e., solid element in ABAQUS versus shell element in IDEA StatiCa). Also, due to the nature of the tie constraint, larger stresses were obtained on the column in the ABAQUS model. In case 2, in which load was applied on the weld lines, much better agreement was observed between the two models. In both models, it was found the weakest component of the connections was weld lines. This is also consistent with the LRFD code design checks.
Predicted von Mises stress between IDEA StatiCa and ABAQUS models; case 1 (top row): shear load was applied on the centroid of the bolt group, and case 2 (bottom row): shear load was applied on the weld lines
2 SEMI-RIGID CONNECTIONS
In this chapter, the design strength capacities of ten semi-rigid connection specimens were calculated following the requirements of the AISC 360 (2016) and AISC Construction Manual (2017). These specimens were selected from the experimental study performed by Azizinamini et al. (1985) in the Department of Civil Engineering at University of South Carolina. All specimens were analyzed using IDEA StatiCa while one of them was analyzed using ABAQUS (2020). Then, the results were compared.
Experimental Study on Semi-Rigid Connections
Several semi-rigid connections comprised of double angles and top and seat beam flanges were subjected to static and cyclic loadings to investigate their moment-rotation behavior. A pair of specimens was tested at the same time as shown in Figure 2.1. One side of the beam sections were bolted to the column and the other side was supported by roller-type seats. The vertical movement of the stub column was allowed by roller guides attached to the top and bottom of the column. The hydraulic actuator was used to apply the load on the column and the connection transferred the load to the beams.
Test set-up used by Azizinamini et al. (1985)
Code Design Calculations and Comparisons
The design strength capacities (\(\phi\)Rn) of the connections were calculated following the requirements of AISC 360 (2016) and AISC Manual (2017). The nominal strength, Rn, and the corresponding resistance factor, \(\phi\) for each connection design LRFD limit state are provided in Chapter J of AISC 360. It is assumed that the top and seat angles provide moment resistance, and the double web angle is used for shear resistance for the connection conservatively.
Design strength capacity of double web-angles
The following 14 design checks were performed according to the LRFD design equations included in AISC 360 or AISC Manual for the design strength capacity of double web-angle.
- Angle (Beam side)
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Shear yielding Eq. J4-3, AISC 360-16
- Shear rupture Eq. J4-4, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Angle (Column side)
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Shear yielding Eq. J4-3, AISC 360-16
- Shear rupture Eq. J4-4, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Resulting tension capacity due prying action Part 9, AISC Manual
- Beam
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Shear yielding Eq. J4-3, AISC 360-16
- Column
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
The design capacity of two double web-angles (in specimens 14S1 and 14S2) were controlled by block shear of the bolts on the angle attached to the beam while bearing and tearout of the bolts on the beam controlled the shear design capacities of the other eight specimens.
Design strength capacity of the top and bottom seat-angles
The following 16 design checks were performed according to the LRFD equations included in AISC 360 or AISC Manual for the design strength capacity of the top- and seat-angle.
- Top- and Seat-Angle (Beam Side)
- Tension yielding Eq. J4-1, AISC 360-16
- Tension rupture Eq. J4-2, AISC 360-16
- Compression Sec. J4.4, AISC 360-16
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Top- and Seat-Angle (Column Side)
- Shear yielding Eq. J4-3, AISC 360-16
- Shear rupture Eq. J4-4, AISC 360-16
- Tension capacity due prying action Page 9-10, AISC Manual
- Beam
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Flexural Strength Sec. F13.1, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Column
- Panel web shear Eq. J10-9, AISC 360-16
- Flange local bending Eq. J10-1, AISC 360-16
- Web local yielding Eq. J10-2, AISC 360-16
- Web local crippling Eq. J10-4, AISC 360-16
The design capacities of all top and seat angles were controlled by tension capacity due prying action on the angle side bolted to the column. The design capacity all top and seat angles were controlled by tension capacity due prying action.
IDEA StatiCa Analysis
The ten test specimens were modeled in IDEA StatiCa and analyzed under a shear force applied a certain distance away from the column. The distance was selected to be equal to the one between the column centerline and the beam support. The beam support is assumed to be at 120 in. away from the column centerline for the first four specimens while it was 72 in. for the other six specimens. All specimens fail because the top angles attached to the column exceed the plastic strain limit which is defined as 5% by the software.
Moment-rotation diagrams together with resistances determined by AISC traditional calculation (blue) and IDEA StatiCa (orange) are shown in the following pictures.
Moment-rotation relationship of Test No: 14S1 (left) and 14S2 (right)
Moment-rotation relationship of Test No: 14S3 (left) and 14S4 (right)
Moment-rotation relationship of Test No: 8S1 (left) and 8S2 (right)
Moment-rotation relationship of Test No: 8S3 (left) and 8S4 (right)
Moment-rotation relationship of Test No: 8S5 (left) and 8S6 (right)
ABAQUS Analysis
In this section, the output results from IDEA StatiCa were compared to those from ABAQUS (2020) software package. In this study, Test No. 14S1 specimen was chosen as a base model. Numerical simulations with almost identical conditions (i.e., in terms of material properties, boundary conditions, and loading) were carried out using both IDEA StatiCa and ABAQUS. The model was initially designed in IDEA StatiCa and then the assembly (including beam, column, web angles, and top and seat angles) was imported to ABAQUS using the IDEA StatiCa’s viewer platform. Afterward, a simplified model for the bolt was designed and added to the ABAQUS model.
Semi-rigid connection model setup in ABAQUS
In ABAQUS, the element type was C3D8R (3D stress, 8-node linear brick, reduced integration), and a total of 562,377 elements were generated in the model.
ABAQUS model mesh densities
The numerical simulations were carried out on four processors (Intel Xenon (R) CPU E5-2698 v4 @ 2.20GHz) and each simulation took approximately 535 minutes to finish.
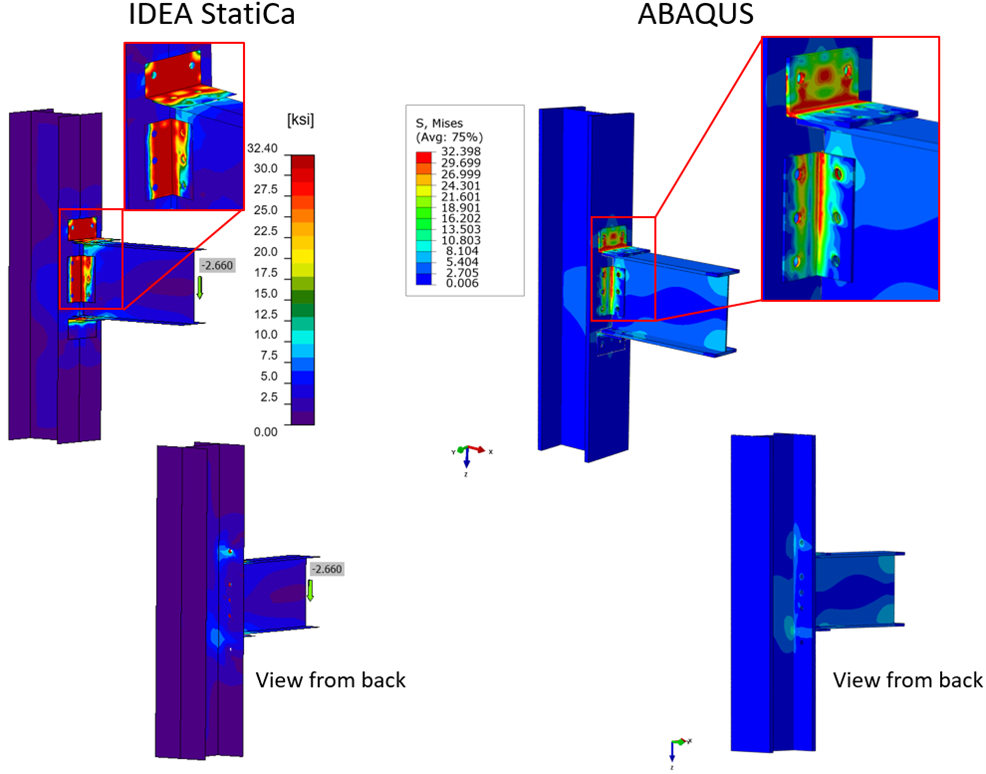
Comparison of the predicted von-Mises stress between IDEA StatiCa and ABAQUS
Side view comparison between IDEA StatiCa and ABAQUS with deformation scale factor of ten
In general, there was good agreement between the results of the two software packages. However, more deformation was captured on the web angles, top, and bottom flanges in the IDEA StatiCa model. Also, the stress distributions on the web angles were slightly different between the two models. This is most likely due to the fact that in the ABAQUS model solid elements with reduced integration were utilized. In both models, it was found that the weakest component of the assembly was the top flange in tension under the applied shear force pointing downward, which introduces tension in the top flange.
3 RIGID CONNECTIONS
In this chapter, the design strength capacities of ten rigid connection specimens were calculated following the requirements of the AISC 360 (2016) and AISC Construction Manual (2017). The baseline specimen was selected from the experimental study performed by Sato et al. (2007) in the Department of Structural Engineering at University of California, San Diego. The baseline specimen and nine additional variation models were analyzed using IDEA StatiCa while the baseline specimen was also analyzed using ABAQUS (2020).
Experimental Study on Rigid Connections
Three full-scale bolted flange plate (BFP) moment connections were subjected to cycling testing at the University of California, San Diego. All specimens met the requirement of AISC Seismic Provisions for Structural Steel Buildings for the beam-column connections of special moment frames. The lateral bracing distance for the specimens was determined in accordance with this provision. The vertical displacements were applied by a hydraulic actuator at the tip of the beam.
Code Design Calculations and Comparisons
The design strength capacities (\(\phi\)Rn) of ten rigid connections were calculated following the requirements of AISC Specification for Structural Steel Buildings (AISC 360, 2016) and AISC Steel Construction Manual (AISC Manual, 2017). The nominal strength, Rn, and the corresponding resistance factor, \(\phi\), for each connection design limit state for load and resistance factor design (LRFD) are provided in Chapter J of AISC 360.
Design strength capacity of single web plates
The following eight design checks were performed according to the LRFD design equations included in AISC 360 or AISC Manual for the design strength capacities of single web plate.
- Web Plate
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Shear yielding Eq. J4-3, AISC 360-16
- Shear rupture Eq. J4-4, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Weld shear Eq. 8-2, AISC Manual
- Beam
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
Out of the calculated design capacities for the ten test specimens, the design capacity of model 2 was controlled by shear rupture while bolt shear led to failure for the other eight specimens.
Design strength capacity of flange plates
The following 13 design checks were performed according to the LRFD design equations included in AISC 360 or AISC Manual for the design strength capacities of flange plates.
- Flange Plate
- Bolts shear Eq. J3-1, AISC 360-16
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Tensile yielding Eq. J4-3, AISC 360-16
- Tensile rupture Eq. J4-4, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Compression Sec. J4-4, AISC 360-16
- Beam
- Bolt bearing and tearout Eq. J3-6, AISC 360-16
- Flexural Sec. F13.1, AISC 360-16
- Block shear Eq. J4-5, AISC 360-16
- Column
- Panel web shear Eq. J10-9, AISC 360-16
- Flange local bending Eq. J10-1, AISC 360-16
- Web local yielding Eq. J10-2, AISC 360-16
- Web local crippling Eq. J10-4, AISC 360-16
Out of the calculated design capacities for the ten test specimens, the design capacity of seven specimens was controlled by web panel zone shear, two specimens were controlled by bolt shear and one specimen was controlled by block shear. The moment capacities of the specimens were calculated by multiplying by the controlling design capacity by the moment arm as provided in Table 3.5. The moment arm is equal to the depth of the beam for bolt shear while it is equal to the summation of the depth of the beam and the thickness of the plate for web panel zone shear and block shear strengths (BFP, models 1, 2, 3, 4, 5, 6 and 8).
IDEA StatiCa Analysis
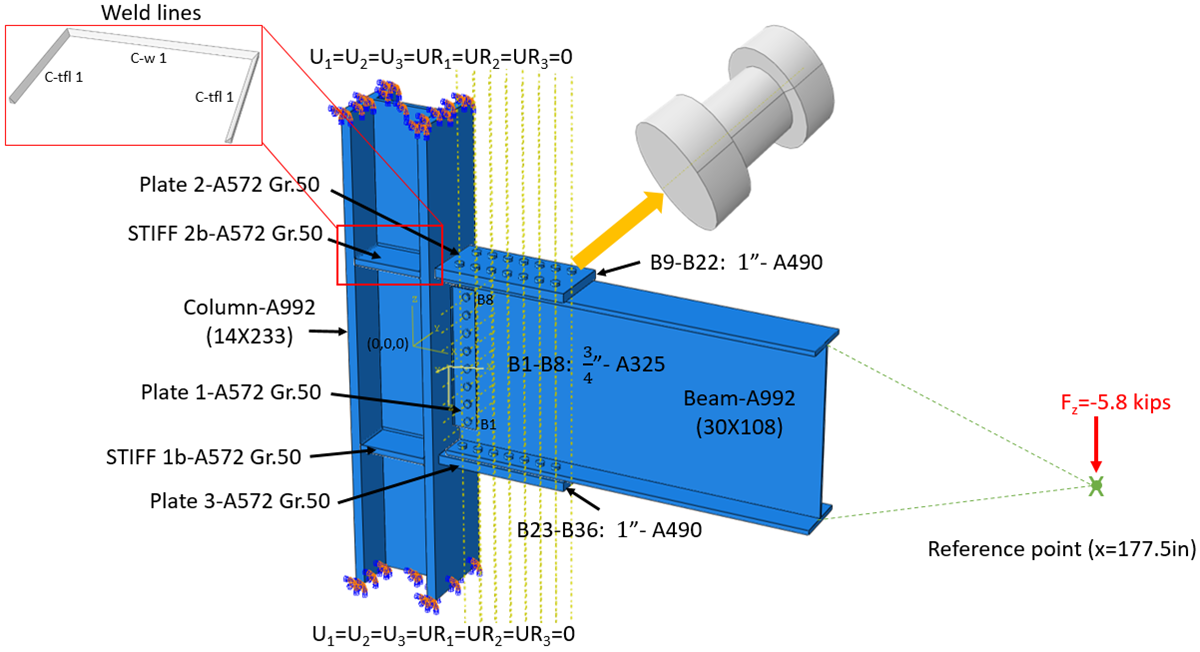
The ten rigid steel connection specimens were modeled in IDEA StatiCa and analyzed under a shear force applied at 177.5 in. away from the column centerline as in the test report. The shear force was increased incrementally until the connections reached their capacities in IDEA StatiCa.
ABAQUS Analysis
In this section the output results from IDEA StatiCa were compared to ABAQUS software package (version 2020). Test BFP was chosen as a base model. Numerical simulations with almost identical conditions (i.e., in terms of material properties, boundary condition, and loading) were carried out using both IDEA StatiCa and ABAQUS. The model was initially designed in IDEA StatiCa and then the assembly (including beam, column, and plates) was imported to ABAQUS using the IDEA StatiCa’s viewer platform. Afterward, a simplified model for the bolt was designed and added to the ABAQUS model.
Model setup in ABAQUS
In ABAQUS, the element type was C3D8R (3D stress, 8-node linear brick, reduced integration), and a total of 681,016 elements were generated in the model. The numerical simulations were carried out on eight processors (Intel Xenon (R) CPU E5-2698 v4 @ 2.20GHz) and the simulation took approximately 685 minutes.
There was a good agreement between the results of the two software packages. The stress distributions on the beam and column were very close. However, slightly higher stresses were predicted on the column, plate 1, and stiffeners in the ABAQUS model which is most likely due to the nature of the tie constraint. The predicted load on the bolts and weld groups were also very close between the two software.
4 SUMMARY AND CONCLUSIONS
IDEA StatiCa is a component-based finite element analysis (FEA) software package for steel connection design. It can be used for structural evaluation or design of a variety of welded and bolted structural steel connections and base plates. The main objective of this report was to verify the FEA results obtained from the IDEA StatiCa software package for three types of steel connections commonly used in the United States (i.e., simple, semi-rigid, and rigid) according to the U.S. building codes. Measured experimental response was available for the connection specimens selected for verification purposes in this study. For each connection type and ten variations of that, first, the code checks and calculations were performed following the requirements of the AISC 360, Specification for Structural Steel Building (2016), and AISC Steel Construction Manual (2017) codes. Then, the results were compared with the IDEA StatiCa predictions. Additionally, the results from the IDEA StatiCa were compared with ABAQUS, which is another robust FEA code in the market. Measured responses of the test specimens were also used to compare and better understand the overall behavior and failure mode of connection models.
In general, there was good agreement between the IDEA StatiCa results, code-checks according to the U.S. codes, and the ABAQUS results. The calculated results are different than those obtained with IDEA StatiCa possibly because AISC is a design code and may be conservative while the software is intended to capture the real behavior which is expected to be more accurate.
While there are many FEA software packages in the market capable of predicting the overall structural response to a variety of loading conditions, there is a lack of specialized FEA tools with a focus on connection design. Compared to other FEA software packages in the market, IDEA StatiCa software has many advantages. In addition to the ease of use, the most important characteristic of IDEA StatiCa was found to be the computational time in which the results can be obtained in a fraction of time compared to the conventional FEA codes such as ABAQUS. This will help the engineers to evaluate and modify their preliminary connection design faster and in a more efficient way if any changes are required. In addition, in common FEA software packages, the loads and capacities of the connection members (i.e., bolts, welds, plates) should be extracted from the model during the post-processing stage which is a cumbersome and time-consuming task. However, in IDEA StatiCa, the results are directly calculated and reported. Also, in IDEA StatiCa, load can be directly applied at any locations/members of the connection, while in typical FEA codes this should be done through defining the reference point and then coupling it with the connection which is an extra step.
A minor discrepancy, however, was found where the contacts defined between the plates and column/beam faces, although the same type of analysis was performed, i.e., small deformation. This could be due to the differences between solid elements and shell elements or contact algorithm(s) that are used in two software. Also, the way that IDEA StatiCa code calculates and utilizes the optimum element size was not clear. Additionally, due to the recommended plastic strain limit of 5% by Eurocode (EN1993-1-5 app. C par. C8 note 1) which is defined as a default value in the IDEA StaiCa software, different failure modes were observed.
Because of IDEA StatiCa’s fast and easy connection modeling and analysis capabilities, complicated nonlinear modeling and time-consuming dynamic analysis of large steel structures can be performed relatively quickly. Properties of the connections in beam-column frame structures can be defined based on the analysis and design checks completed in IDEA StatiCa. Then, the connection model can be revised and re-analyzed if necessary after the frame analysis is completed using a structural analysis software, e.g., SAP2000. The connections can be made weaker or stronger in IDEA StatiCa depending on the desired optimum performance of the structural frame model. An easy and more robust approach to develop connection moment-rotation response in IDEA StatiCa will be very helpful because in programs like SAP2000 moment-rotation response of connections need to be defined as part of modeling of frame structures.
IDEA StatiCa software is only as good as its Graphical User Interface. If the GUI is not well executed, users will have trouble with using the application or the software. IDEA StatiCa design it well. Along with a good GUI — the quality of the software is also observed. Following a set of conventions or standards ensures consistency and makes it easy for users to navigate in the software. A standard and consistent language ensures users will understand terms when they see them. Models are easily modified, allowing fast variable exploration and checking.
The software consistently updates including faster load times, and even bug fixes to improve the overall user experience.
References
[1] AISC (2016). “Specification for Structural Steel Buildings,” American Institute of Steel Construction ANSI/AISC 360-16, Chicago, Illinois.
[2] AISC (2017). “Steel Construction Manual,” 15th edition, American Institute of Steel Construction, Chicago, Illinois.
[3] McMullin, K. M., & Astaneh-Asl, A. (1988). Analytical and experimental studies of double-angle framing connections. Structural Engineering, Mechanics, and Materials, Department of Civil Engineering, University of California, Berkeley.
[4] ABAQUS 2020, Dassault Systemes Simulia Corporation, Providence, RI, USA.
[5] IDEA StatiCa s.r.o., Sumavska 519/35, Brno, 602 00 Czech Republic; https://www.ideastatica.com/support-center/general-theoretical-background
[6] Azizinamini, A., Bradburn, J. H., and Radziminski, J. B. (1985). Static and cyclic behavior of semi-rigid steel beam-column connections. University of South Carolina.
[7] Sato, A., Newell, J., and Uang, C. M. (2007). Cyclic testing of bolted flange plate steel moment connections for special moment frames. Final Repor to American Institute of Steel Construction.
The full version of the report may be downloaded in the link below:
Attached Downloads
- Final Report_OSU.pdf (PDF, 7.2 MB)