Singularities vs. stress concentration area
The sharp corner created at the junction of the coupling beam and shear wall creates a local stress peak that skews the model results. This peak is caused by the singularities at the point of the sharp re-entrant corner. The question is how to deal with these peaks in the models themselves.
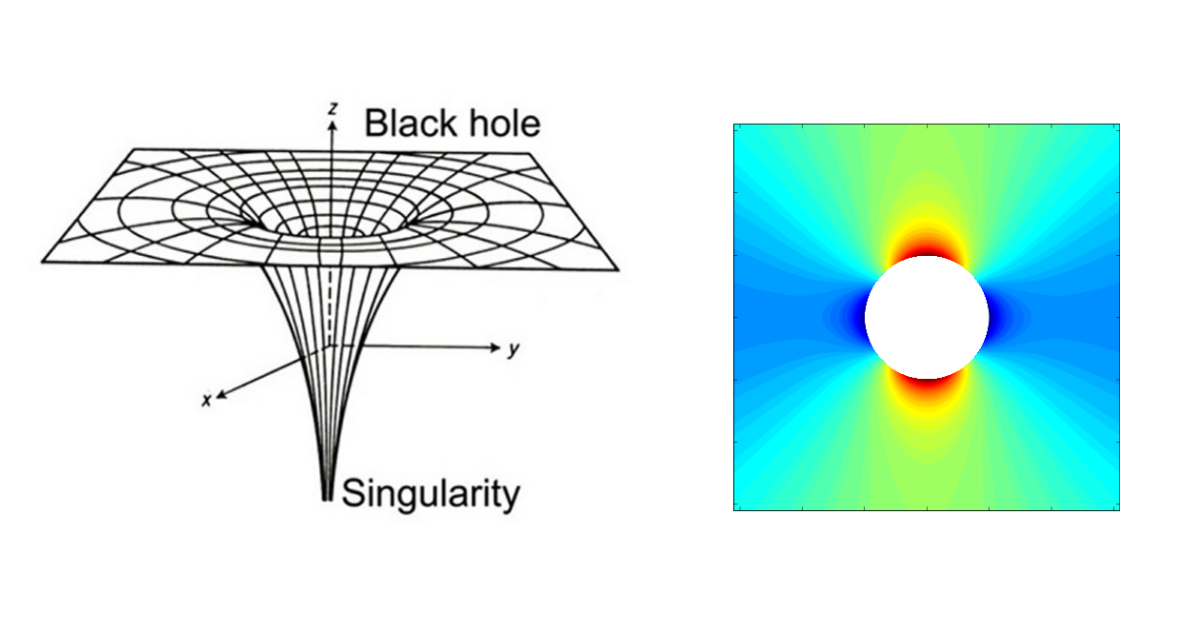
Singularities
A stress singularity is a point of the mesh where the stress does not converge towards a specific value. As we keep refining the mesh, the stress at this point keeps increasing. Theoretically, the stress at the singularity is infinite. Typical situations where stress singularities occur are the appliance of a point load, sharp re-entrant corners, corners of bodies in contact, and point restraints.
In reality, no corner is perfectly sharp. Even if detailed this way, a manufactured sharp corner will always present a small fillet radius. This means that the stress will not be infinite anymore and the corner singularity will disappear. Instead, stress concentration takes over.
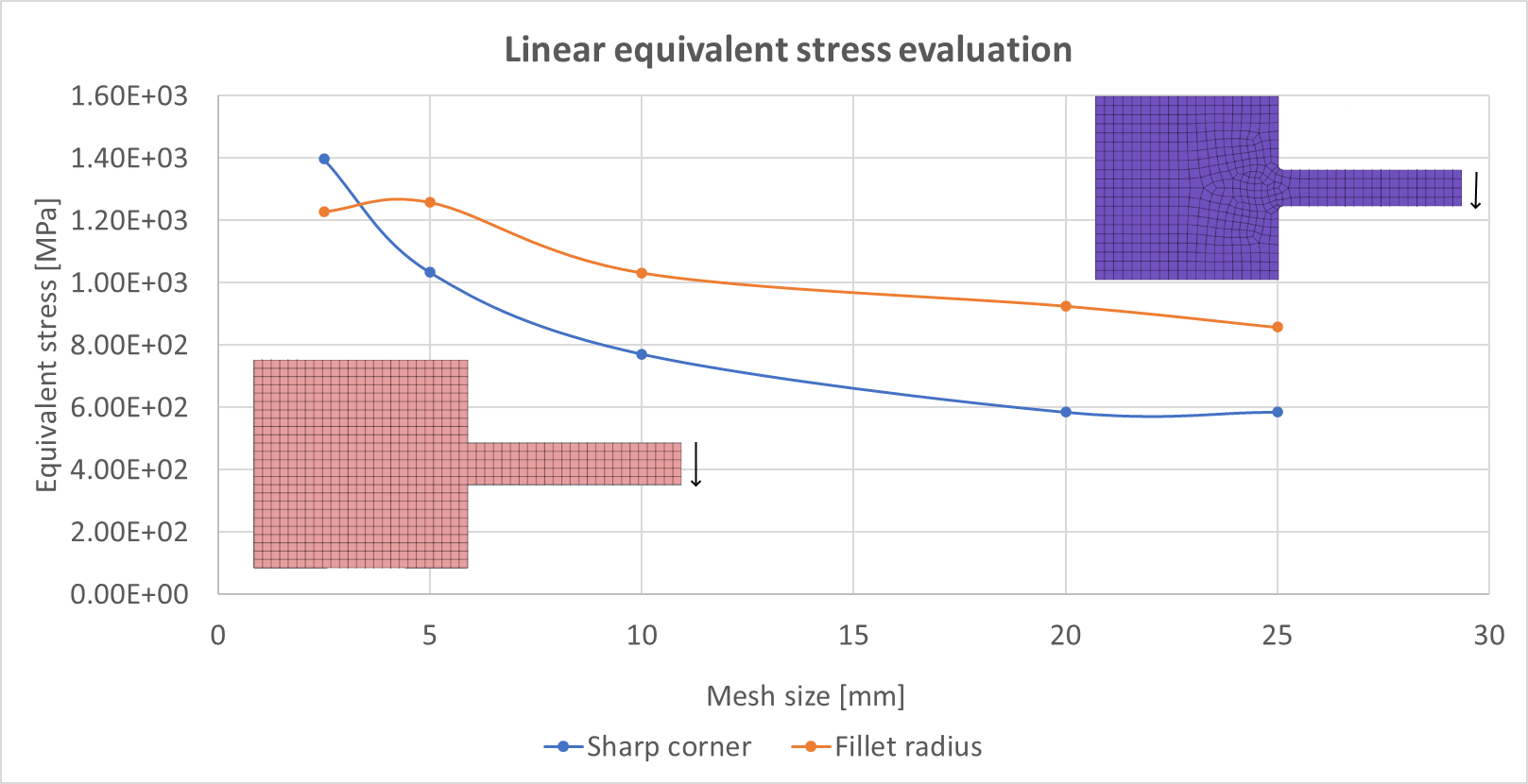
Figure 6. A sensitivity study was performed on the material linear model to find the relationship between mesh stress concentration behavior.
Stress concentration
Stress concentration behaves similarly to stress singularities, but the stress will converge towards a finite value, not infinite, given that the mesh is sufficiently refined. Features such as holes, filleted corners, changes of cross-section, etc., will lead to stress concentrations.
- A coarse mesh will not capture local effects such as stress concentrations.
- The more we refine the mesh, the more accurate the results are. However, the model is not computationally efficient. The Saint Venant's principle says that the effect should be local. Therefore, the mesh could be refined locally rather than globally, subdividing all the elements in the mesh.
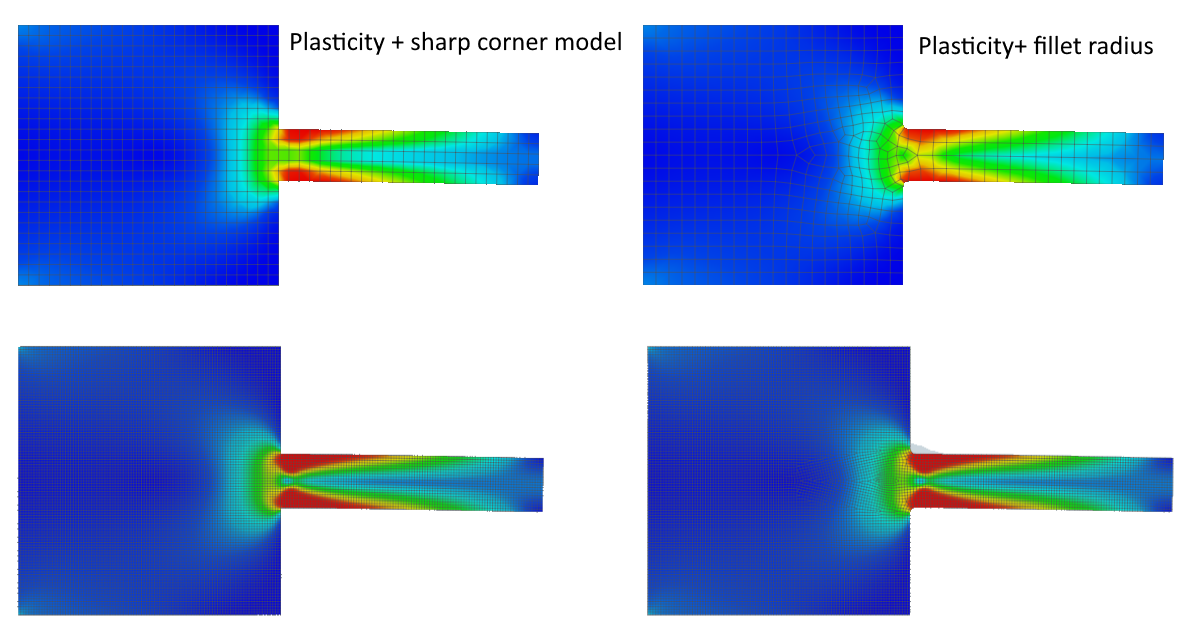
- Plasticity helps to ensure correct behavior and suppress the singularity effect.
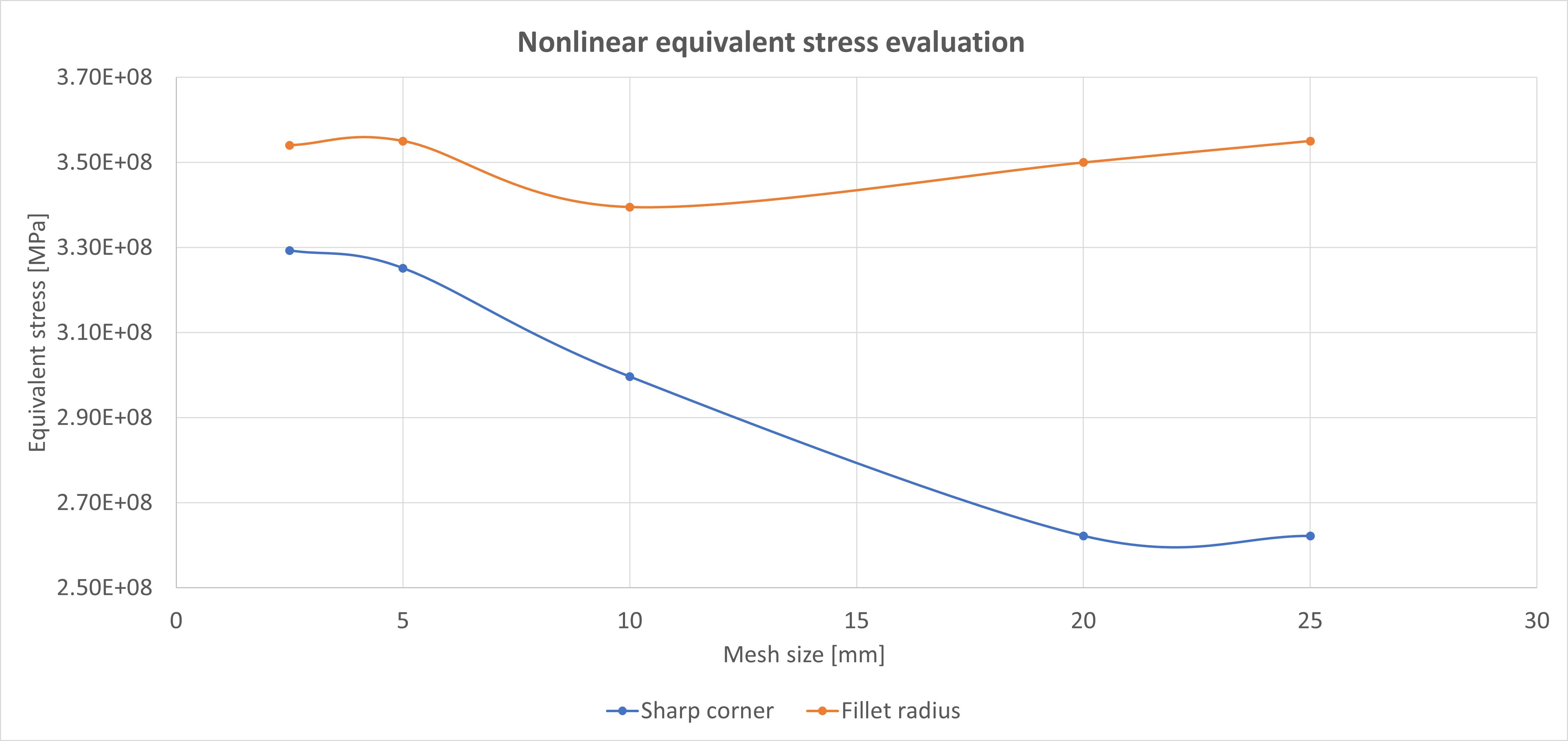
Figure 7. A sensitivity study was performed on the material nonlinear model to find the relationship between mesh size and sharp and fillet corner equivalent stress.
How to deal with singularities and stress concentrations
- Ignore the singularities. If we are interested in the stresses far away from any singularities, the Saint Venant's principle applies – the stresses will be correct.
- The mesh must be locally refined to capture the stress concentration effect.
- Typical geometric-induced singularities, such as sharp re-entrant corners, can be avoided by modeling fillets instead. Effectively, the stress singularity becomes a stress concentration.
- Plasticity allows the model to behave according to reality, and the singularity effect vanishes.
- The mesh should be refined to verify that stresses do converge. This requires a mesh sensitivity study.