1. The objective
The objective of this article is the verification of the LBA (linear bifurcation analysis) module of the IDEA Member application. Beams in bending are analyzed and the influence of different loading conditions is investigated. The resulting elastic critical moments from IDEA Member are compared to the elastic critical moments based on Annex I of EN 1999-1-1 [1]. Numerical solutions from ANSYS [2] and LTBeam [3] software are also presented.
2. Model description
A total of 18 individual cases was analyzed to verify the LBA module. All of them share the same cross-section IPE 240 and the same steel grade S 235. Three different loading conditions were investigated (A – end moments, B – force in the middle, C – continuous load). Six relative slenderness values were verified ranging from 0.6 to 1.6.
Fig. 1: Various boundary conditions and load cases used for verification
3. Analytical solution
The three-factor formula found in Annex I of EN 1999-1-1 is used to calculate the elastic critical moment for lateral-torsional buckling of the beams:
\[ M_{cr} = \mu_{cr} \frac{\pi \sqrt{E I_z G I_t}}{L} \]
\[ \mu_{cr} = \frac{c_1}{k_z} \left [ \sqrt{1+\kappa_{wt}^2 + (C_2 \zeta_g - C_3 \zeta_j)^2} - (C_2 \zeta_g - C_3 \zeta_j) \right ] \]
Fig. 2: Buckling mode of a simply supported beam (C_5)
4. Results
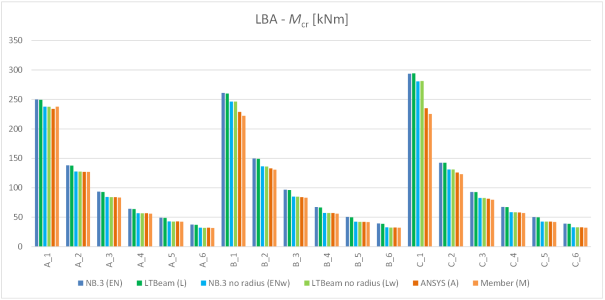
The elastic critical moment from IDEA Member (M) is compared to an analytical value for a rolled cross-section (EN) and for its representation without the web-flange radii (ENw). Furthermore, the same two sets of values are presented as an output from the LTBeam software [3] (L – with radii, Lw – without radii). Finally, results from the ANSYS software [2] without radii (A) are presented.
Tab. 1: Resulting elastic critical moments
The results of LBA are conservative (5-23 %) compared to the Eurocode and are in good agreement with other software solutions.
Chart 1: Elastic critical moment values
Chart 2: Elastic critical moment comparison
The conservative results of IDEA Member are caused by the missing web-flange radii of the shell representation of a cross section in IDEA Member and resulting lower beam torsional stiffness. This is confirmed by the LTBeam software (Lw), as well as the analytical solution (ENw) and a solution in ANSYS (A).
5. Literature and References
[1] EN 1999-1-1: Eurocode 9: Design of aluminium structures - Part 1-1 : General structural rules, CEN, 2006.
[2] Aa, R.P. van der: Numerical assessment of the design imperfections for steel beam lateral torsional buckling, Master thesis, report 2015.96, Eindhoven University of Technology, Eindhoven, Dept. of the Built Environment, Structural Design, The Netherlands, 2015.
[3] LTBeam software v. 1.0.11, CTICM, available at https://www.cesdb.com/ltbeam.html