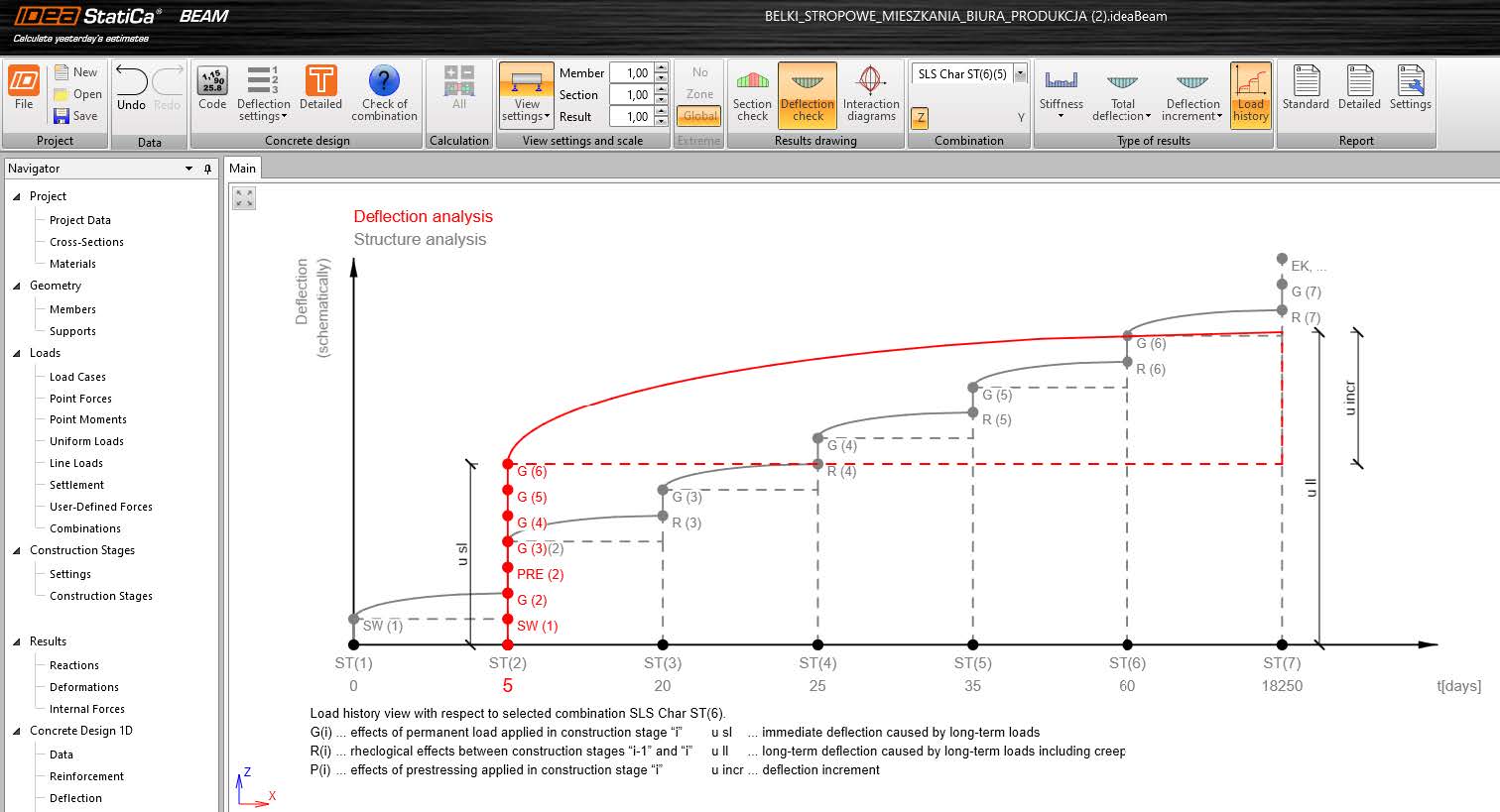
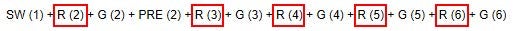Deflection check in IDEA StatiCa Beam
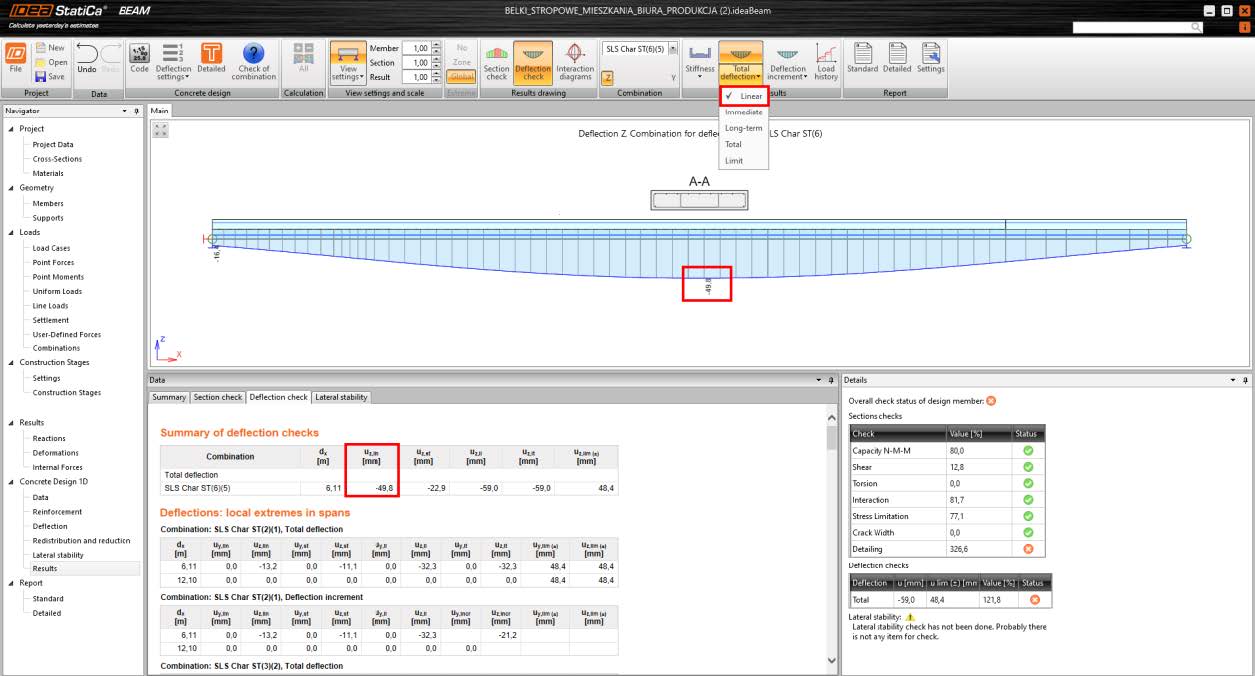
The Beam application provides four types of deflection results:
- Linear
- Immediate (Short-term)
- Long-term
- Total
Linear deflection
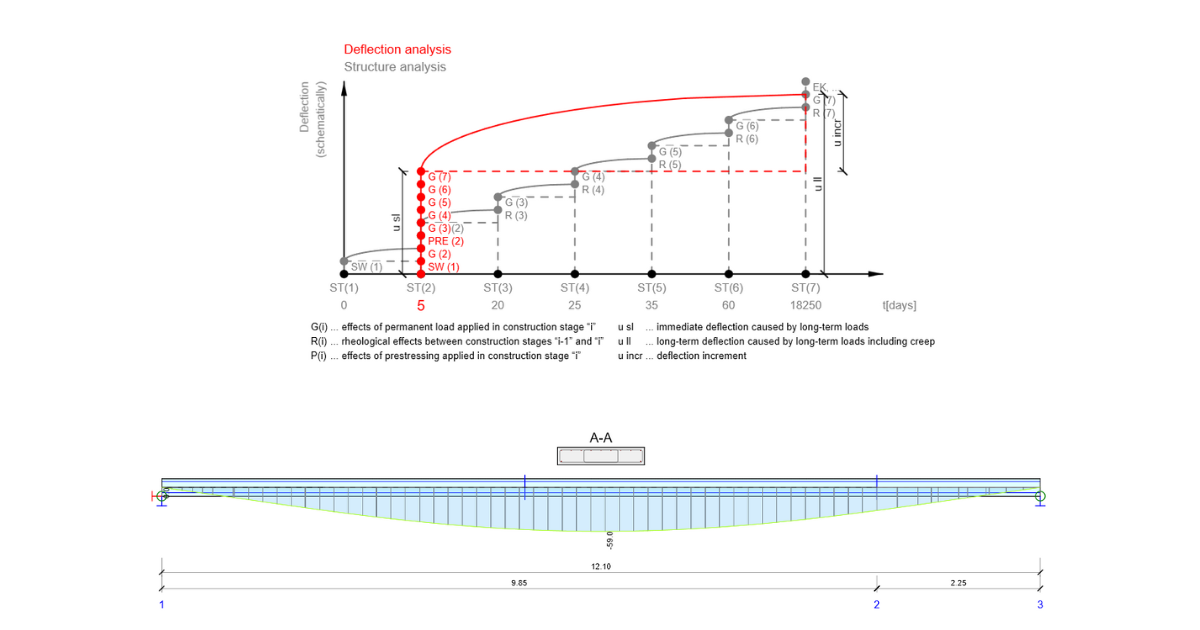
Linear deflection is calculated as a summation of all deflections of particular load cases (permanent, prestressing, and rheological) assigned for the selected combination. Deflection and internal forces are calculated for each load case separately, considering the actual static system with the support position defined in each construction stage.
There are several differences compared to other deflection calculation types (immediate, long-term, total):
- The stiffness of the cross-section is considered linear (without cracks), and reinforcement is neglected.
- Results for particular load cases are calculated by TDA analysis, and Young's modulus of concrete is considered as Ec(t) (tangent modulus).
- Rheological phenomenons (such as creep, shrinkage, and relaxation) are calculated by the TDA analysis, and results are presented in rheological load cases signed “R”
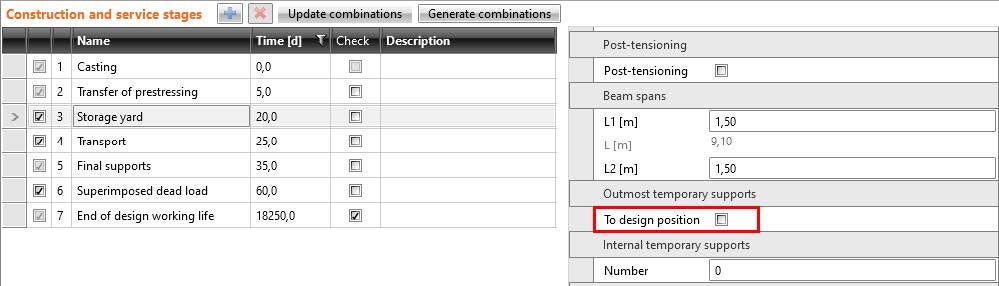
The change of support position during construction can also influence results, mainly if the option “To design position” is deactivated. This setting can be defined for each construction stage up to the “Final supports” stage.
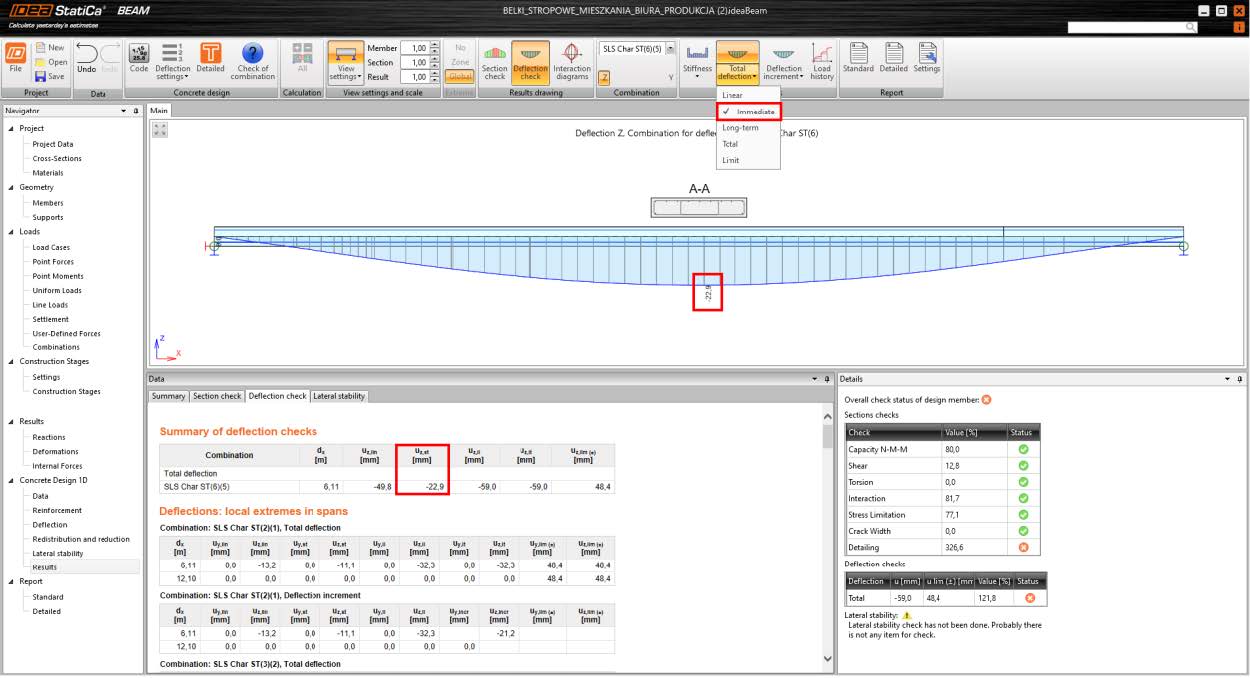
Immediate deflection
Immediate deflection is a short-term nonlinear deflection due to characteristic load combination, taking into account crack development.
Basic assumptions for the calculation:
- The reinforcement layout is considered.
- Rheological phenomenons (creep, shrinkage, and relaxation) are neglected.
- All permanent and prestressing loads are applied to the resulting structural system (defined in the “Final supports” stage. Therefore, the change of support during construction does not affect the result of deflection.
Long-term deflection
Long-term deflection is a long-term nonlinear deflection due to a quasi-permanent load combination, taking into account crack development.
Basic assumptions for the calculation:
- The reinforcement layout is considered.
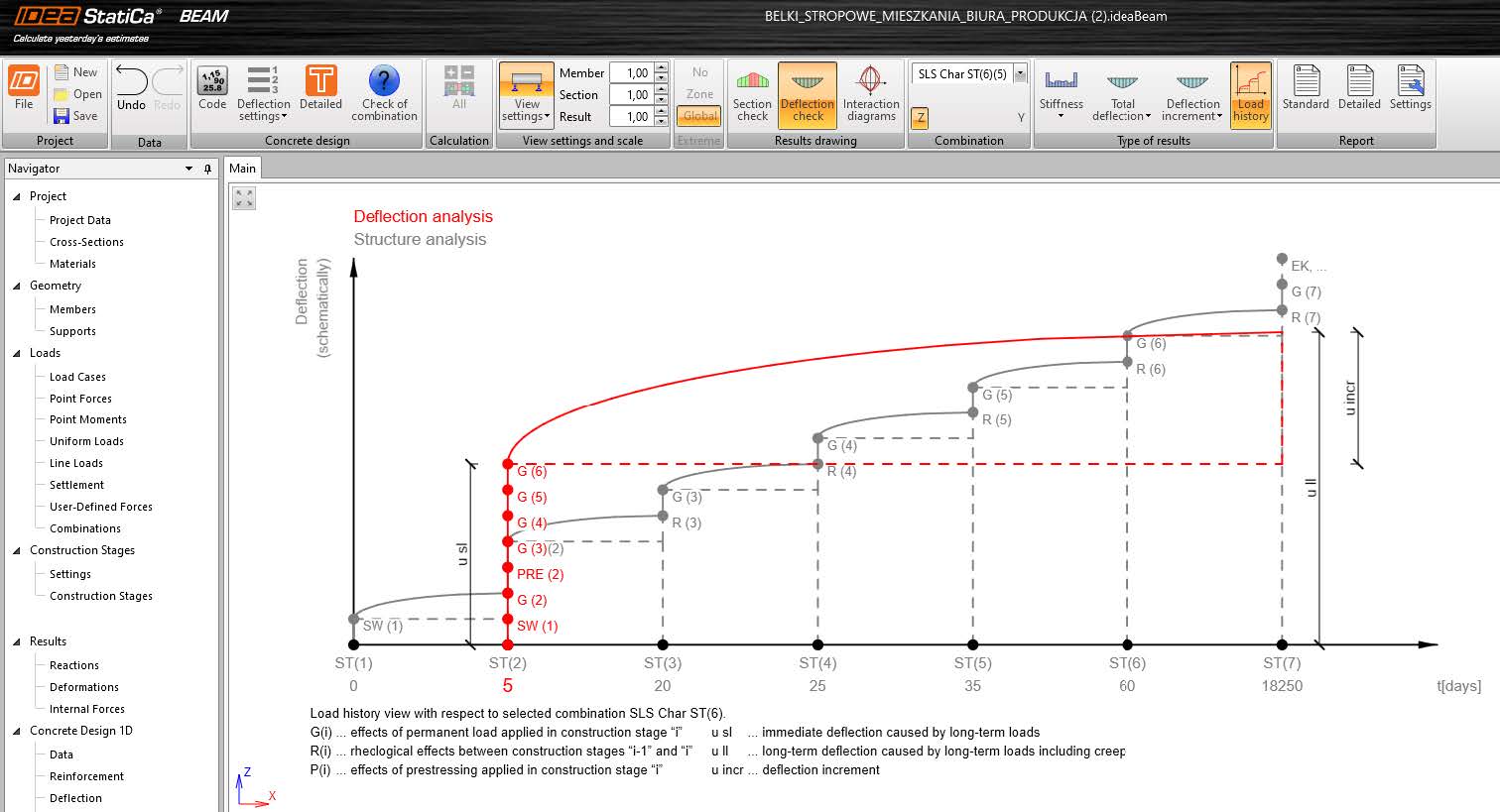
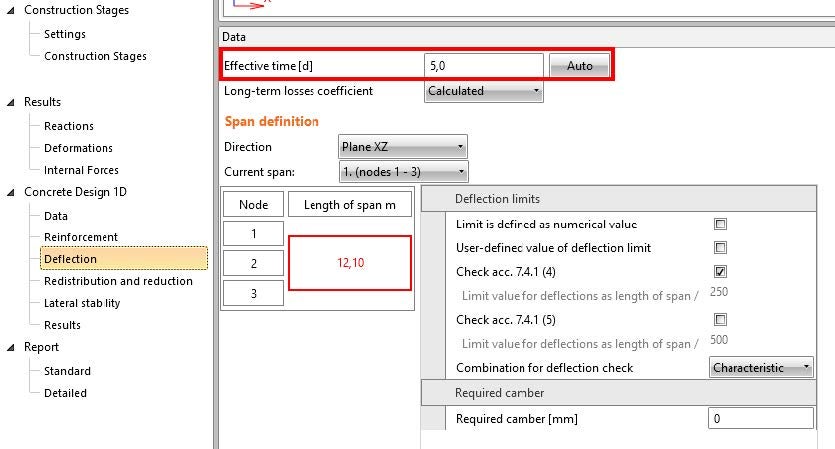
- Creep effects are calculated by applying all considered permanent and prestressing loads to the structure, whose stiffness is influenced by the effective Young´s modulus of concrete Ec,ef. All loads are applied at the same time, as defined in the section “Deflection”.
The time when all permanent and prestressing loads are applied to the structure is presented in the “Load history”.
Shrinkage effects are calculated as a curvature of the beam caused by the shrinkage and take into account the designed reinforcement layout. Deflection due to shrinkage is calculated on the final structural system.
\[{\left( {\frac{1}{r}} \right)_{cs}} = {\varepsilon _{cs}} \cdot {\alpha _{e,cs,ef}} \cdot \frac{{{S_{cs,ef}}}}{{{I_{cs,ef}}}}\]
All permanent and prestressing loads are applied to the resulting structural system (defined in the “Final supports” stage. Therefore, the support change during construction does not affect the result of non-linear deflection.
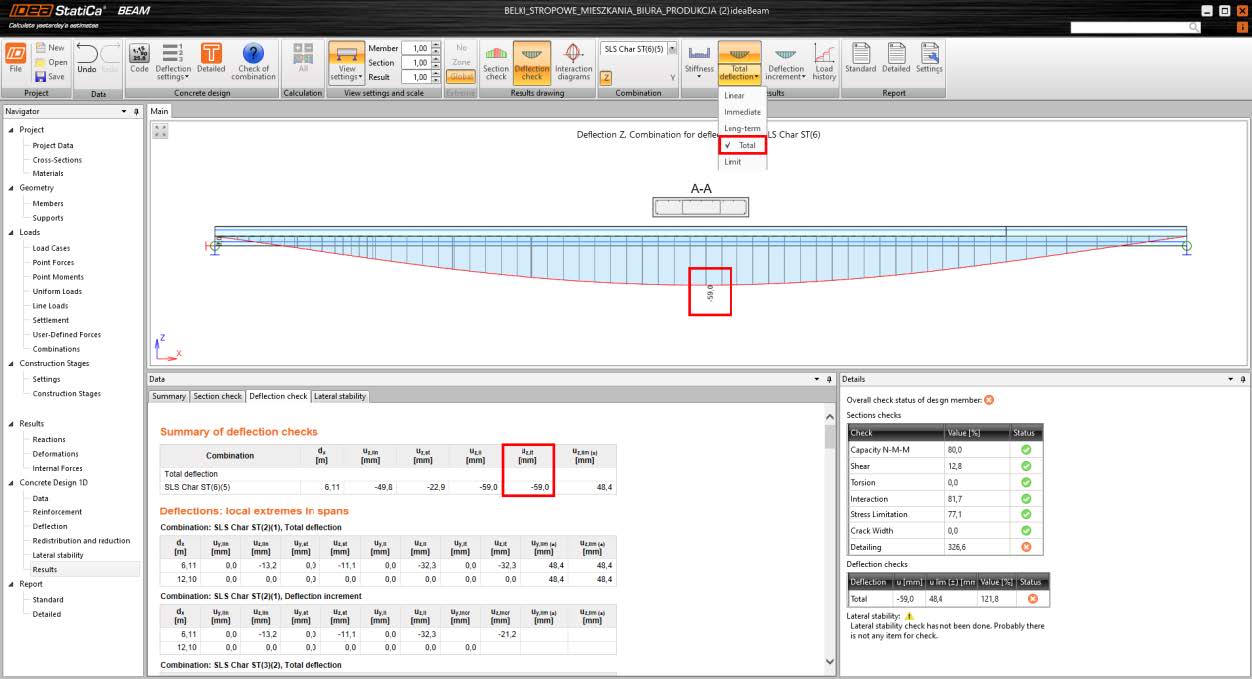
Total deflection
Total deflection is a long-term nonlinear deflection due to a characteristic load combination, considering crack development.
Basic assumptions for the calculation:
- The reinforcement layout is considered.
- Creep effects are calculated by applying all considered permanent and prestressing loads to the structure, whose stiffness is influenced by the effective Young's modulus of concrete Ec,ef. All loads are applied at the same time, as defined in the section “Deflection”.
The time when all permanent and prestressing loads are applied to the structure is presented in the “Load history”.
- If the selected characteristic combination also contains variable loads, the part of these loads is considered long-term, and it's applied to the structure with long-term stiffness as described for the permanent load. The remaining variable load is considered short-term and applied to structures with relevant short-term stiffness (Ecm for concrete is assumed).
- Shrinkage effects are calculated as a curvature of the beam caused by the shrinkage and taking into account the designed reinforcement layout. Deflection due to shrinkage is calculated on the final structural system.
\[{\left( {\frac{1}{r}} \right)_{cs}} = {\varepsilon _{cs}} \cdot {\alpha _{e,cs,ef}} \cdot \frac{{{S_{cs,ef}}}}{{{I_{cs,ef}}}}\]
All loads are applied to the resulting structural system (defined in the “Final supports” stage. Therefore, the change of support during construction does not affect the result of non-linear deflection.