Code-check of welds according to Russian standards
It is possible to set butt welds or fillet welds and along the full edge length, partial welds or intermittent welds. Butt welds are assumed to have the same strength as the welded member and are not checked. In case of fillet welds, the weld element is inserted between interpolation links connecting plates to each other. The weld element has a specified elasto-plastic material diagram to redistribute the stress along the weld length so that the long welds, multi-orientation welds or welding to unstiffened flange have similar resistance as according to hand calculation. The most stressed weld element is decisive in the weld check.
The most stressed fillet weld element of the weld is checked according to SP 16, Cl. 14.1. The length of the weld should be decreased by 10 mm according to SP 16, Cl. 14.1.16.
Weld metal check:
\[ \frac{N}{\beta_f k_f l_{we} R_{wf} \gamma_c} ≤ 1.0 \]
Base metal check:
\[ \frac{N}{\beta_z k_f l_{we} R_{wz} \gamma_c} ≤ 1.0 \]
where:
- N – force acting on a weld element
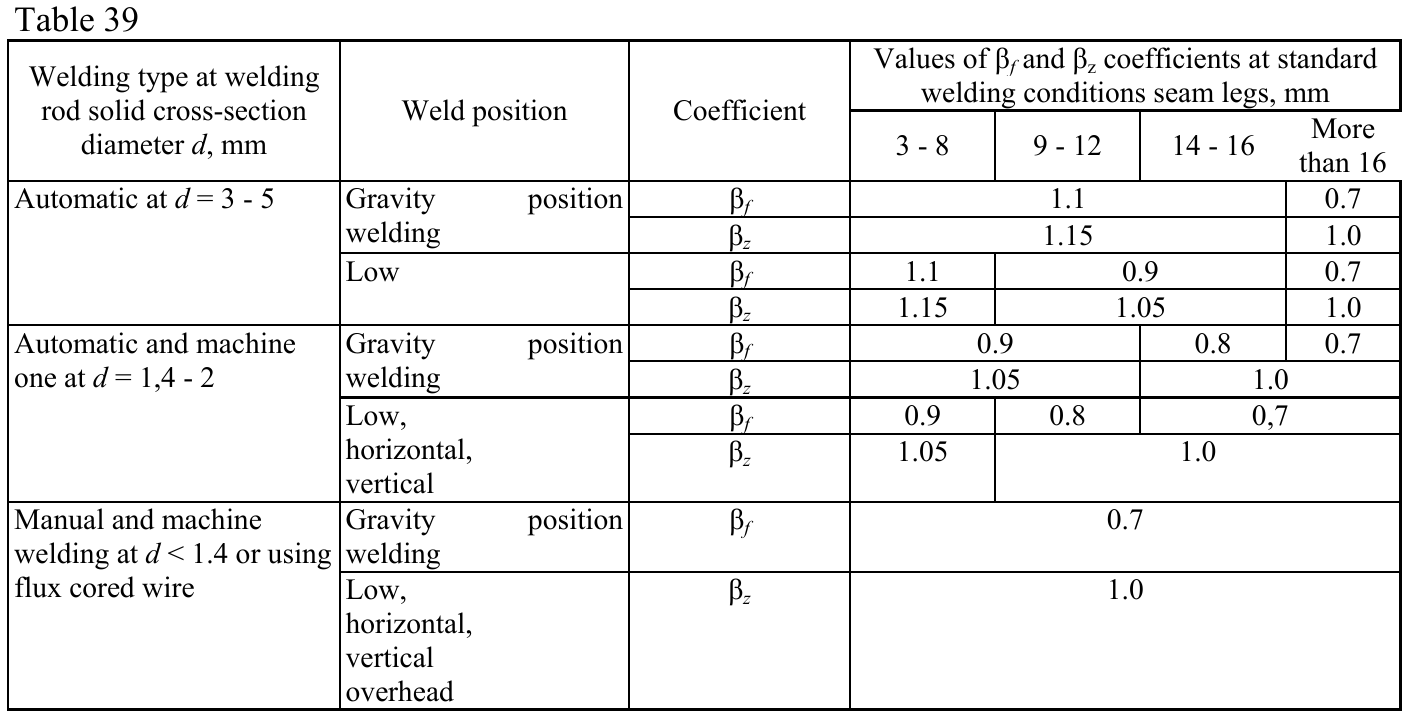
- βf – coefficient for weld metal from SP 16, Table 39; coefficient is determined by Code setup – type of welding and welding position (settings of weld material)
- βz – coefficient for base metal from SP 16, Table 39; coefficient is determined by Code setup – type of welding and welding position (settings of weld material)
- kf – weld leg size, fillet weld leg ratio is assumed 1:1
- \( l_{we} = \frac{l_w}{l} \cdot l_e \) – design weld element length
- lw = l – 10 mm – design weld length
- l – actual weld length
- le – actual weld element length
- \( R_{wf} = 0.55 \frac{R_{wun}}{\gamma_{wm}} \) – weld metal ultimate strength – SP 16, Table 4
- Rwz = 0.45 Run – base metal ultimate strength – SP 16, Table 4
- γc – service factor – SP 16, Table 1, editable in Code setup
- Rwun – standard strength of fillet weld metal from SP 16, Table D2
- γwm – partial safety factor for weld metal, γwm = 1.25 for Rwun ≤ 490 MPa and γwm = 1.35 otherwise – SP 16, Table 4
- Run – characteristic strength of connected steel
| Welding material | Rwun [MPa] | Rwf [MPa] |
| E42 | 410 | 180 |
| E46 | 450 | 200 |
| E50 | 490 | 215 |
| E60 | 590 | 240 |
| E70 | 685 | 280 |
| E85 | 835 | 340 |
The gravity type of weld position may be set at the selection of welding electrode and the welding type in the Code setup.
The weld diagrams show stress according to the following formula:
\[ \sigma = \sqrt{ \sigma_{\perp}^2 + \tau_{\perp}^2 + \tau_{\parallel}^2 } \]