Interaction code-check advancements in RCS
In the following article, we will explain the approach to the calculation of the longitudinal force caused by shear Ftd,s. This method consists mainly of changing the way the force is applied to the cross-section. We start with the definition of the cross-section subjected by N-My-Mz and then we gradually add the longitudinal force caused by shear and torsion.
Response N-My-Mz
The cross-section is, in the first phase, loaded by a combination of normal force and bending moments N-My-Mz. The results comparison between the software versions provides us with the same results.
If the shear reinforcement is designed in the cross-section, shear can be resisted by a fictitious strut-and-model composed of stirrups, concrete struts, and longitudinal rebars.
Calculated longitudinal force due to shear is applied to the cross-section with all components (concrete and rebars). The initial stress state taken from the N+My+Mz response is already defined for each component.
The equation for the calculation of the longitudinal force due to shear:
\[\Delta F_{td,s} = V_{ed}(cot \theta -cot \alpha ) \]
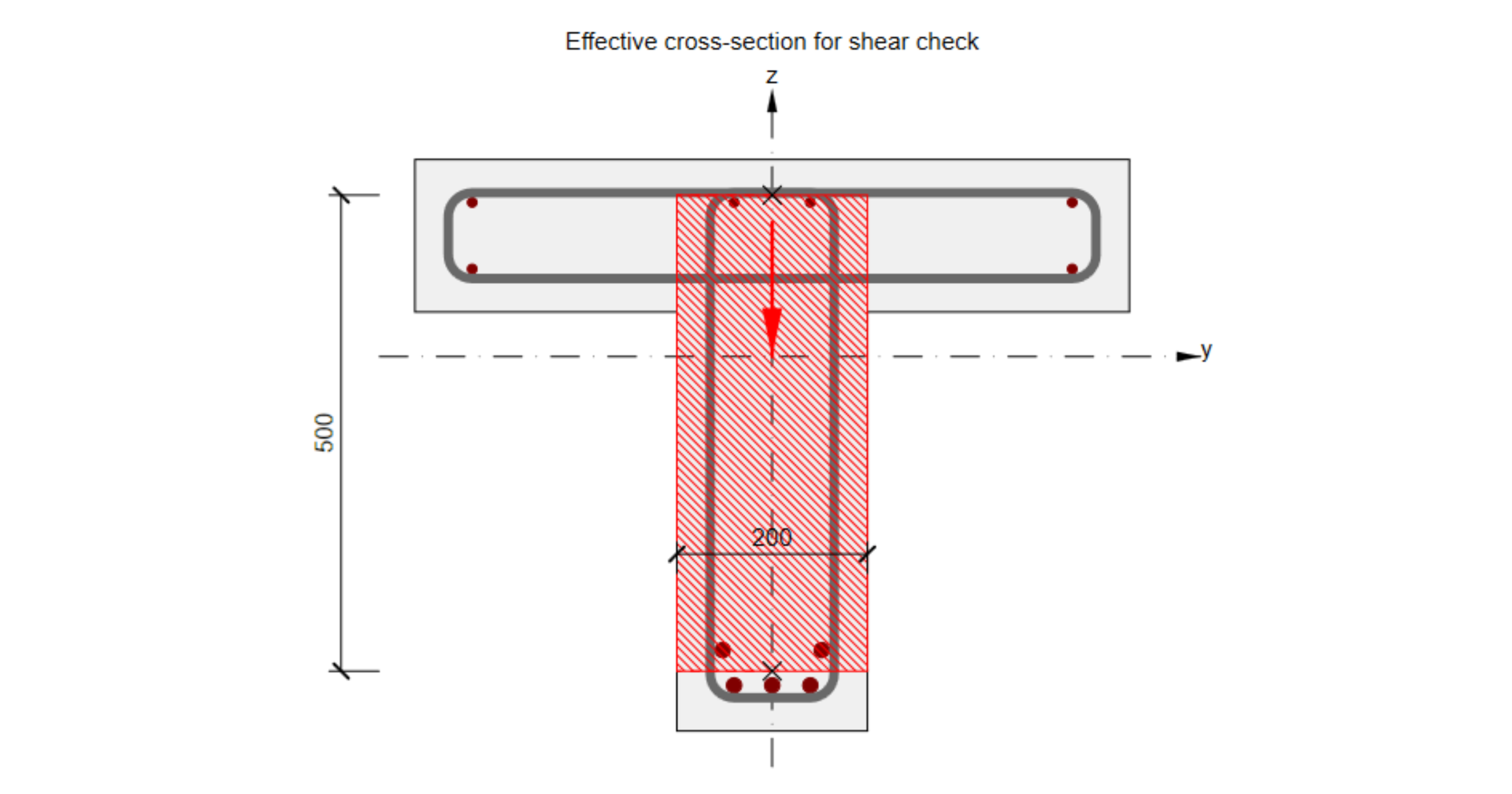
Longitudinal force Ftd,s is, by default, applied to:
- The centroid of the section resisting shear – for the cross-sections where the application is able to define such a section (the red area in the following figure).
- The centroid of the cross-section – for the cross-sections where the application is not able to define such a section.
Interaction N-My-Mz-Vz
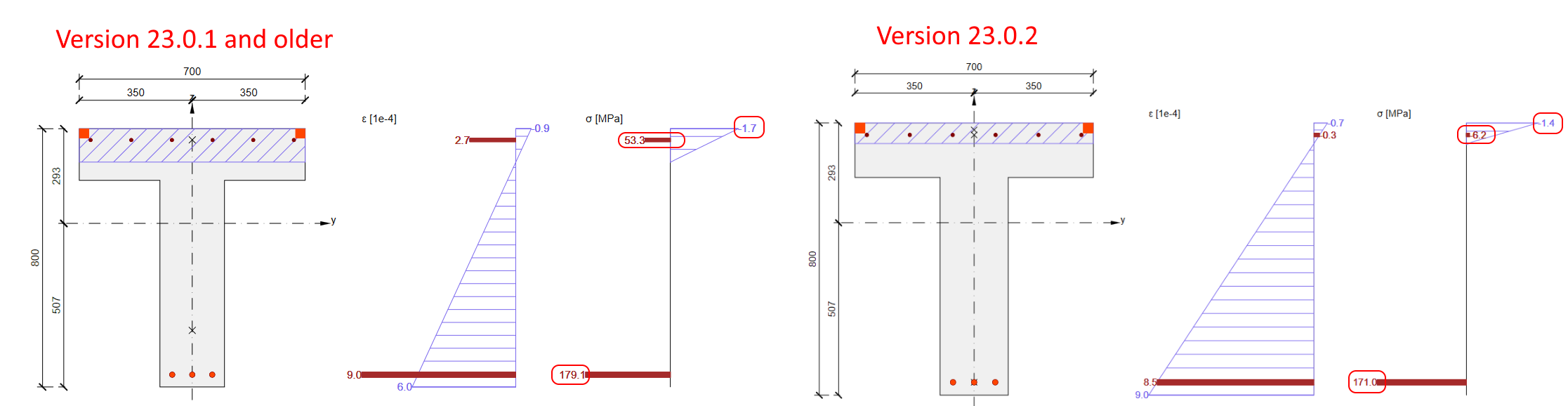
The sectional response due to the combination of N+My+Mz+ΔFtd,s is calculated. We can notice that the stress in concrete and rebars in compression decreased while the stress in tensile reinforcement increased (in comparison with response N+My+Mz). The section is still in equilibrium.
Interaction N-My-Mz-Vz-T
For sections also subjected to torsion, we apply an additional longitudinal tensile force ΔFtd,t to longitudinal rebars lying inside the stirrup selected for torsion check. The calculation model is slightly different because we assume that the section is composed of longitudinal rebars while neglecting the concrete. The N+My+Mz+ΔFtd,s response defines each rebar's initial stress state. Consequently, ΔFtd,t is applied, following the condition of the same strain increment for all rebars resisting torsion.
The assumptions for the calculation mean that in some cases, like sections located above the intermediate support of a continuous beam, different results can be observed. When the stress in tensile reinforcement due to N+My+Mz reached yield stress, other less utilized rebars carried the longitudinal force due to shear (e.g., located in a compression zone).
Available in IDEA StatiCa Concrete and IDEA StatiCa Complete editions.