Šrouby a šroubové spoje

Model šroubu dle CBFEM

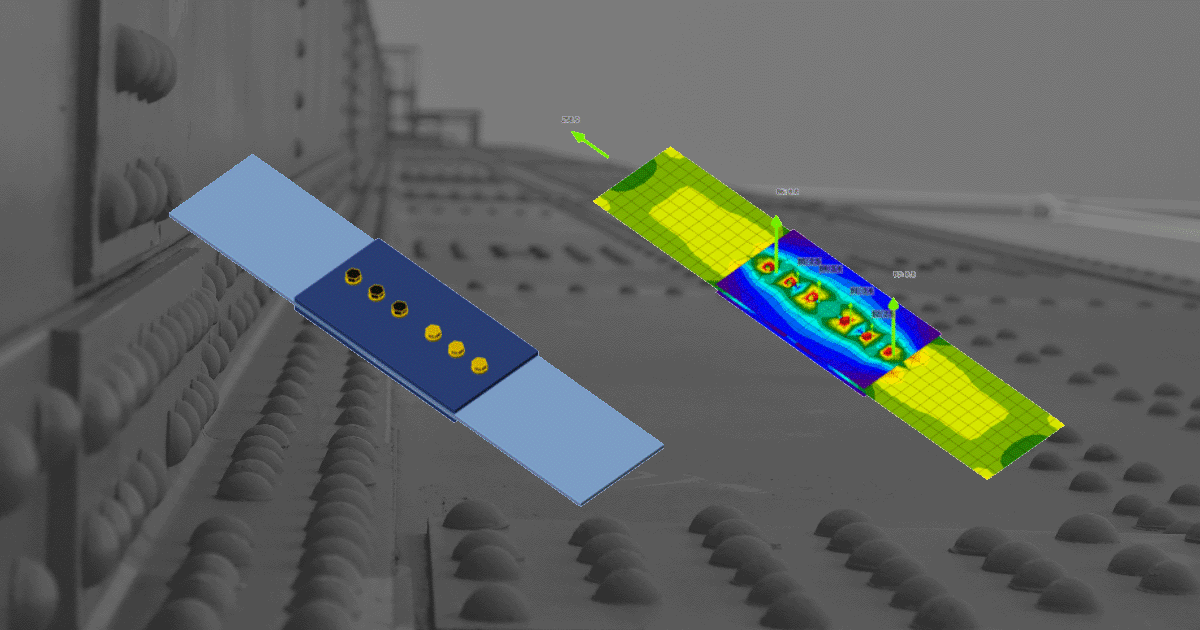
IDEA StatiCa má ve svém řešiči jedinečnou metodu, komponentní metodu konečných prvků (CBFEM). Model šroubu použitý v CBFEM je popsán a ověřen dle několika národních norem pro ocel. Celková únosost a deformace  jsou rovněž porovnávány s hlavními experimentálními výzkumnými programy.

V komponentní metodě konečných prvků (CBFEM) je šroub s jeho chováním v tahu, tlaku a smyku komponentou, popsanou závislými nelineárními pružinami. Šroub v tahu je popsán pružinou s její axiální počáteční tuhostí, návrhovou pevností, mezí kluzu a  velikostí deformace. Pro stanovení meze kluzu a velikosti deformace se předpokládá, že k plastické deformaci dochází pouze v závitové části dříku šroubu.

V našich teoretických základech najdete další informace o tom, jak metoda CBFEM popisuje a ověřuje šrouby. Pokud se chcete o CBFEM dozvědět něco více, je rozhodně nejlepší pročíst si General theoretical background.

Šrouby dle národních norem

Pojďme se podívat na to, jak CBFEM přistupuje k šroubům z hlediska jednotlivých návrhových norem. IDEA StatiCa zatím podporuje osm národních norem, které řeší návrh a/nebo konstrukční zásady šroubů a předpjatých šroubů.

Posouzení šroubů a předpjatých šroubů dle Eurokódu

Počáteční tuhost a únosnost šroubů ve smyku jsou v CBFEM modelovány podle Cl. 3.6 a 6.3.2 v EN 1993-1-8. Pružina představující tah a tlak ve šroubu má bi-lineární silově-deformační chování s počáteční tuhostí a návrhovou únosností dle Cl. 3.6 a 6.3.2 v EN 1993-1-8.

Konstrukční zásady 

Kontrola umístění šroubů se provádí, pokud je v záložce Norma vybrána tato možnost. Zkontrolují se rozměry od středu šroubu k okrajům desky a mezi šrouby. Vzdálenost od okraje e = 1.2 a vzdálenost mezi šrouby p = 2.2 jsou doporučeny v tabulce 3.3 v EN 1993-1-8. Uživatelé mohou obě hodnoty upravit v záložce Norma.

Posouzení šroubů a předpjatých šroubů dle AISC

Síly ve šroubech jsou stanoveny analýzou konečných prvků. Mezi tahové síly patří i páčicí síly. Únosnost šroubů se kontroluje dle AISC 360 - kapitola J3.

Konstrukční zásady  

Je zkontrolována minimální vzdálenost mezi šrouby a vzdálenost od středu šroubu k okraji připojené části. Minimální rozestup 2,66krát (možná úprava v záložce Norma) jmenovitý průměr šroubu mezi středy šroubů  je zkontrolován dle AISC 360-16 - J.3.3. Minimální vzdálenost od středu šroubu k okraji připojeného dílu se kontroluje dle AISC 360-16 - J.3.4; hodnoty jsou v tabulce J3.4 a J3.4M.

Posouzení šroubů a předpjatých šroubů dle jiných norem

• Posouzení šroubů a předpjatých šroubů dle CISC (Kanada)
• Posouzení šroubů  a předpjatých šroubů dle čínské normy (GB)
• Posouzení šroubů a předpjatých šroubů dle Hong Kong normy (HKG)
• Posouzení šroubů a předpjatých šroubů dle IS 800 (Indie)
• Posouzení šroubů a předpjatých šroubů dle SP (Rusko)
• Posouzení šroubů a předpjatých šroubů dle AS (Austrálie)

Konstrukční zásady 

Jak nastavit vzdálenosti

Vzdálenosti od okrajů použité pro únosnost šroubů musí být relevantní pro obecné geometrie desek, plechů s otvory, výřezy atd.

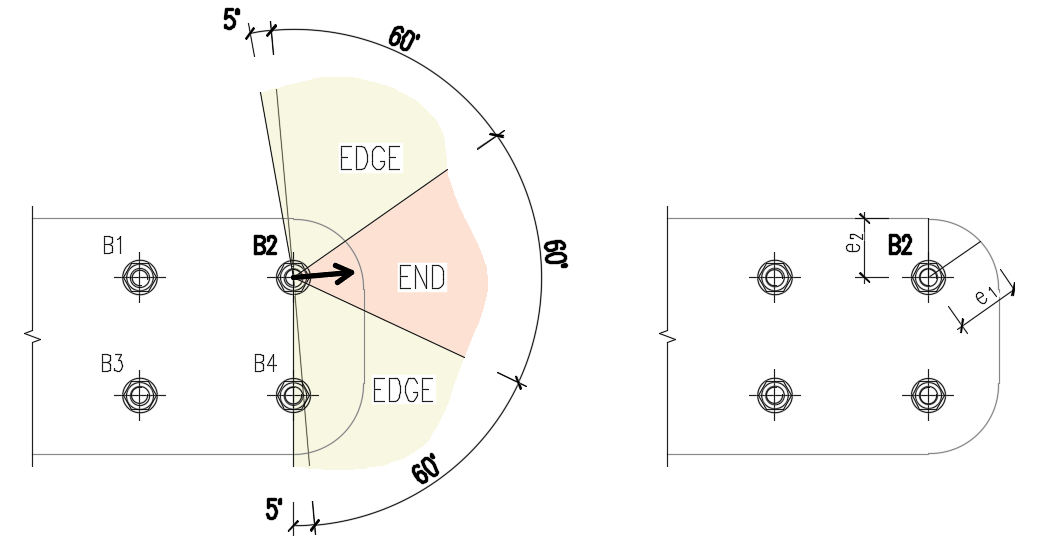
V rámci posudku algoritmus zjistí skutečný směr výslednice smykových sil pro daný šroub a následně vypočítá vzdálenosti nutné pro posouzení šroubu.

Vzdálenosti šroubu k okrajům (e1, e2) jsou určeny rozdělením okraje plechu do tří segmentů. Koncový segment uprostřed je vyseknut úhlem 60° ve směru vektoru síly. Krajní segmenty jsou pak definovány každý úhlem 65° kolmo na vektor síly. Následně je nalezena nejkratší vzdálenost mezi šroubem a příslušným segmentem, a ta vstupuje do výpočtu jako vzdálenost k jednomu, resp. druhému okraji.

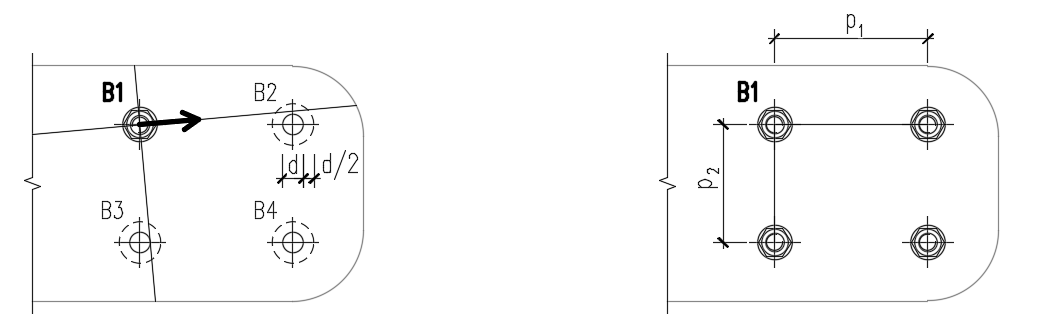
Rozteče mezi jednotlivými šrouby (p1; p2) se automaticky vypočtou pomocí následujícího postupu: díry okolních šroubů se myšleně zvětší o polovinu průměru šroubů. Zároveň se šroubem vedou dvě pomocné přímky: jedna ve směru vektoru smykové síly a druhá kolmo na něj. Hodnoty p1 a p2 jsou pak velikosti úseček mezi šroubem a místem, kde přímky protnou zvětšené otvory sousedních šroubů.

Verifikační příklady

Připravili jsme několik verifikačních příkladů ověření pro kontrolu výsledků ve srovnání s jinými výpočetními metodami.

EN

• Bolted connection - Splices in shear
• Bolted connection - Interaction of shear and tension
• Haunched joint – capacity design

AISC

• Bolted splice connection
• Bolted flange plate moment connection – LRFD
• Extended moment end-plate connection – ASD

Patentovaná technologie pro stavební inženýry

Víte, že naše modelové řešení šroubu je součástí amerického patentu? Přečtěte si zde náš příběh o úspěchu

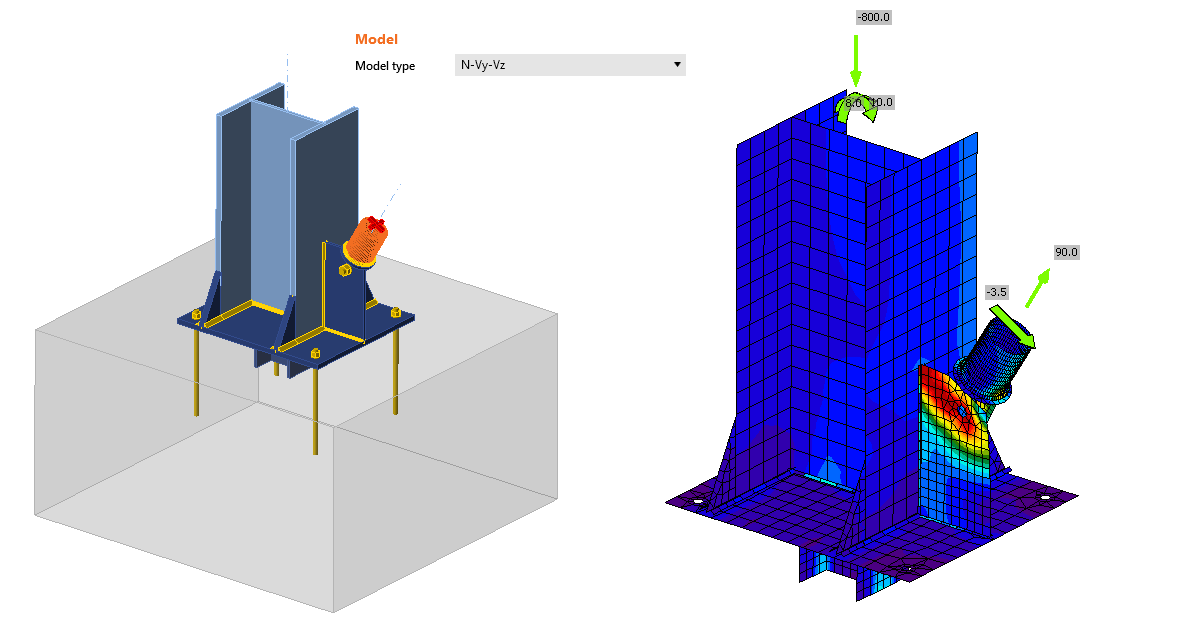
 Přípoj jedním šroubem - naše řešení 

Někdy musí inženýr udělat přípoj pouze s jedním šroubem, zvláště pokud potřebuje namodelovat závěs, výztuhu nebo diagonálu. Chcete-li modelovat a spočítat tento druh operace, musíte definovat správný typ modelu. Více o tom si můžete přečíst zde.

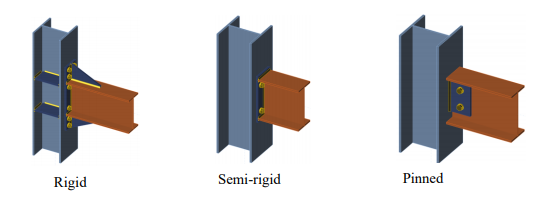
Šrouby, svary a tuhost přípoje

Šrouby i svary mají své výhody a nevýhody. Jedním z důležitých aspektů při výběru spoje je jeho plánovaná tuhost. Obecně platí, že šroubový spoj nikdy tak tuhý jako svařovaný spoj. Pokud zvolíte šroubový spoj, doporučujeme spočítat tuhost takového přípoje a zohlednit výslednou tuhost v celkové konstrukci. Zde si můžete přečíst, jak takový výpočet vypadá a co to obnáší, nebo se podívat na toto video.