Code-check of bolts and preloaded bolts according to Chinese standard
Bolts
Bolts are checked according to GB 50017, Cl. 11.4. The tensile and shear force in each bolt is determined by finite element analysis. Prying forces are determined by finite element analysis and taken into account. Each shear plane is checked individually. The plate in the bearing is checked against the sum of shear forces at nearby planes.
Design tensile and shear strengths of a bolt; fub[MPa] – ultimate strength of a bolt; derived from Table 4.4.6
| \(f_{ub}\) [MPa] | \(f_t^b \) | \(f_v^b\) |
| \(f_{ub} \le 400 \) | \(0.425 \cdot f_{ub}\) | \(0.35 \cdot f_{ub}\) |
| \(400<f_{ub}<830\) | \(0.42 \cdot f_{ub}\) | \(0.38 \cdot f_{ub}\) |
| \(830 \le f_{ub}\) | \(40/83 \cdot f_{ub}\) | \(32/83 \cdot f_{ub}\) |
Bolt in tension
A bolt subject to a tensile force is designed according to Cl. 11.4.1.2 and shall satisfy:
\[ N_t \le N_t^b = A_s \cdot f_t^b \]
where:
- Nt – tensile force in a bolt
- Ntb – design tension capacity
- \( A_s = \frac{\pi d_e^2}{4} \) – tensile stress area of a bolt
- de – effective diameter of a bolt at threaded section
- ftb – design tensile strength of a bolt
Bolts in shear
A bolt subject to a shear force is designed according to Cl. 11.4.1.1 and shall satisfy:
\[ N_v \le N_v^b = A_g \cdot f_v^b \]
where:
- Nv – shear force in a bolt in investigated plane
- \( A_g = \frac{\pi d^2}{4} \) – gross cross-section area of a bolt
- d – nominal diameter of a bolt
- fvb – design shear strength of a bolt
Each shear plane is checked individually, i.e. number of shear planes nv = 1.
Bolts in combined tension and shear
A bolt loaded in shear and tensile forces at the same time is designed according to Cl. 11.4.1.3 and shall satisfy:
\[ \sqrt{\left ( \frac{N_v}{N_v^b} \right ) ^2 + \left ( \frac{N_t}{N_t^b} \right ) ^2} \le 1.0 \]
where:
- Nv – shear force in a bolt in investigated plane
- Nt – tensile force in a bolt
- Nvb – design shear resistance of a bolt
- Ntb – design tensile resistance of a bolt
Bolts in bearing
A plate subject to a bearing force due to a bolt in shear is designed according to Cl. 11.4.1.1 and shall satisfy:
\[ N_v \le N_c^b = d\cdot t \cdot f_c^b \]
where:
- Nv – shear force in acting on a plate; vector sum of shear forces in nearby planes
- d – nominal bolt diameter
- t – plate thickness
- fcb – design bearing strength of a plate
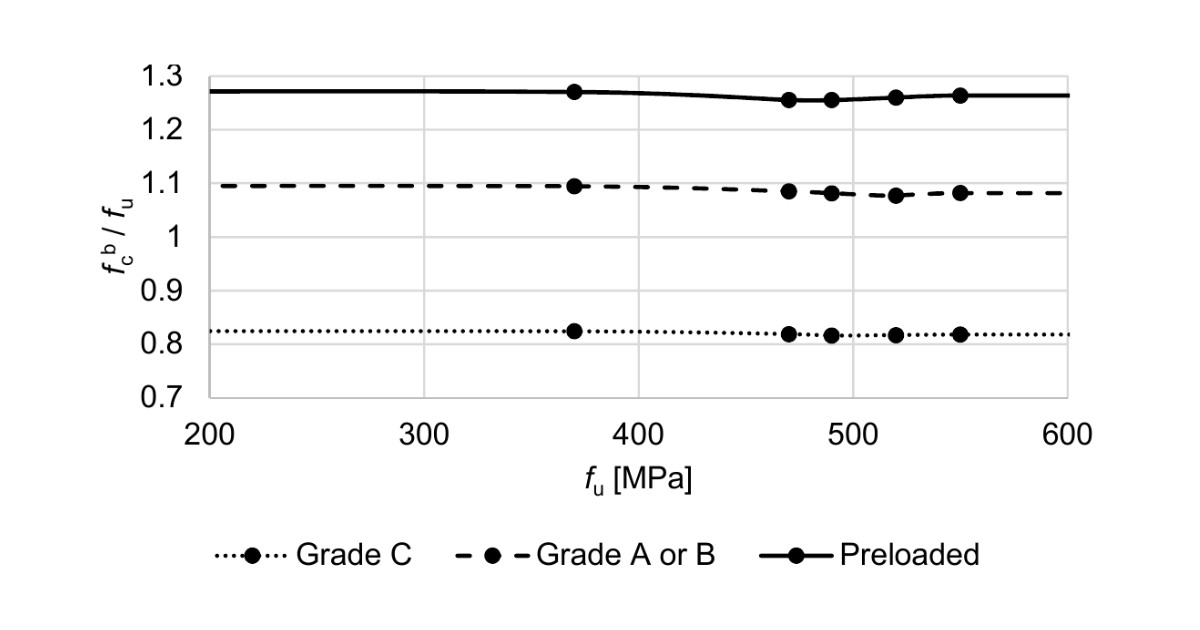
Design bearing strength of a plate; fu – ultimate strength of a plate; derived from Table 4.4.6
Preloaded bolts
High strength bolt in friction type joint is designed according to Cl. 11.4.2.
Preloaded bolts in tension
The tensile resistance of a preloaded bolt is determined as:
\[ N_t \le N_t^b = 0.8 \cdot P \]
where:
- Nt – tensile force in a bolt
- Ntb – design tension capacity
- P – pretension of a high strength bolt – Table 11.4.2-2
Table 11.4.2-2 – pretension of a high strength bolt P [kN]
| Bolt grade | M16 | M20 | M22 | M24 | M27 | M30 |
| 8.8 | 80 | 125 | 150 | 175 | 230 | 280 |
| 10.9 | 100 | 155 | 190 | 225 | 290 | 355 |
A preloaded bolt which is not in Table 11.4.2-2 subject to a tensile force is designed according to Cl. 11.4.1.2 and shall satisfy:
\[ N_t \le N_t^b = A_s \cdot f_t^b \]
where:
- Nt – tensile force in a bolt
- Ntb – design tension capacity
- \( A_s = \frac{\pi d_e^2}{4} \) – tensile stress area of a bolt
- de – effective diameter of a bolt at threaded section
- ftb – design tensile strength of a bolt
Preloaded bolts in shear
The design resistance of a preloaded bolt in shear is determined according to Cl. 11.4.2.1:
\[ N_v \le N_v^b = 0.9 k \mu P \]
where:
- Nv – shear force in investigated plane
- Nvb – design shear resistance of a bolt
- k – factor for bolt holes; k = 1 for normal holes, k = 0.85 for oversized holes, k = 0.6 for slotted holes
- μ – slip coefficient at friction interface taken from Table 11.4.2-1; editable in Code setup
- P = Ntb / 0.8 – pretension of a high strength bolt for bolts which are not in Table 11.4.2-2
Each shear plane is checked individually, i.e. number of shear planes nf = 1.
Preloaded bolts in combined tension and shear
A bolt loaded in shear and tensile forces at the same time is designed according to Cl. 11.4.2.3 and shall satisfy:
\[ \frac{N_v}{N_v^b} + \frac{N_t}{N_t^b} \le 1.0 \]
where:
- Nv – shear force in investigated plane
- Nt – tensile force in a bolt
- Nvb – design shear resistance of a bolt
- Ntb – design tensile resistance of a bolt