GMNA Geometricky nelineární analýza
Geometricky nelineární analýza není při navrhování ocelových styčníků obvykle nutná. Existují dvě výjimky:
- Styčníky dutých průřezů
- Případy, kdy je stabilita rozhodující pro návrhvzpěrem
Jinak je geometricky lineární analýza při malých deformacích (plastická deformace je nižší než 5 %) dostačující, protože výsledky s geometrickou nelinearitou a bez ní jsou téměř totožné.
Geometrická nelinearita je obecně blíže realitě, ale může být vzdálenější od předpokladů návrhu. Široce se používá při navrhování konstrukcí, např. rámy s nízkým součinitelem vzpěru by měly být modelovány pomocí geometricky nelineární analýzy a imperfekcí ve tvaru horizontálního posunu styčníků.
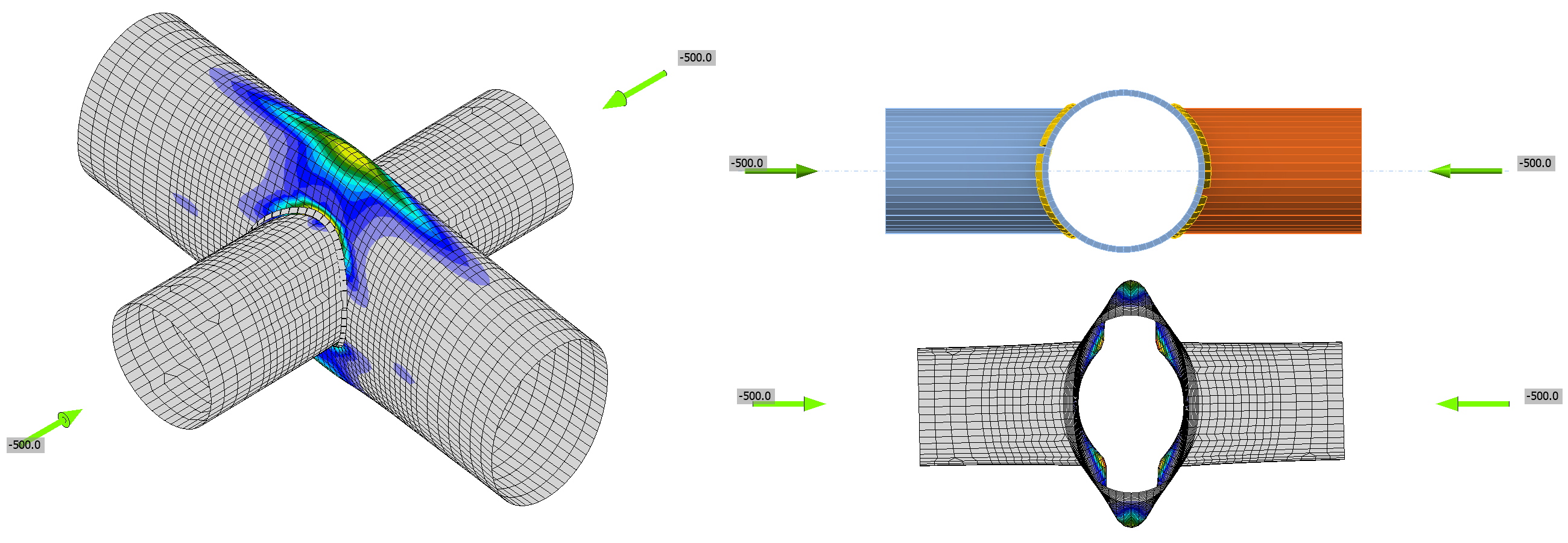
Styčníky dutých průřezů
Styčníky dutých průřezů jsou náchylné k boulení. Skořepina dutého profilu je v přípoji příčně tlačená a díky účinku II. řádu (geometrické nelinearitě) se zvětšuje deformace skořepiny a s touto deformací roste rovněž ohybové namáhání. To je důležité zejména u nejčastějších způsobů porušení, kterými jsou porušení povrchu pásu a porušení boční stěny pásu. Pro styčníky dutých průřezů se důrazně doporučuje používat GMNA.
Případy, kdy je rozhodující stabilita
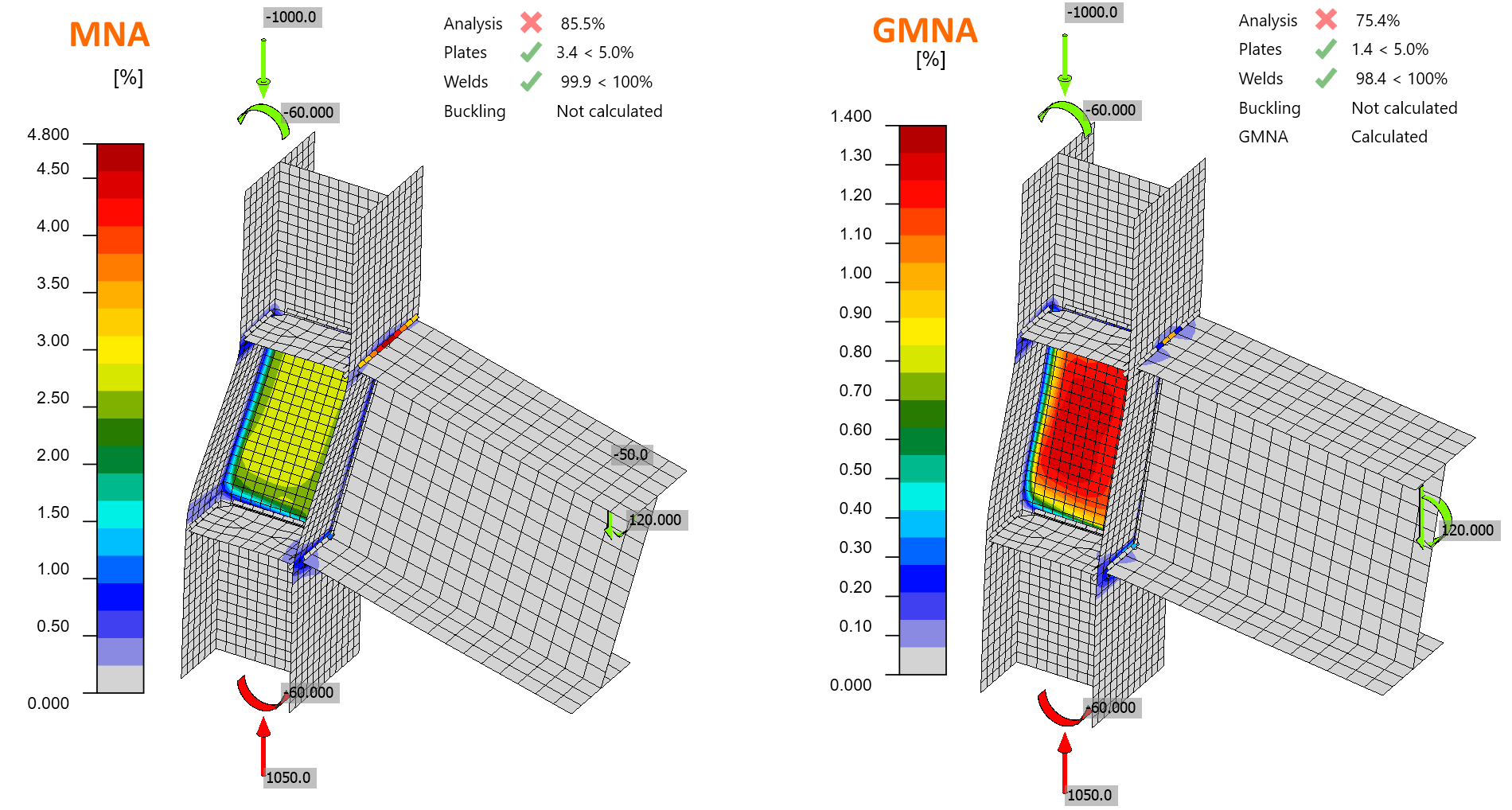
Existují případy, kdy stabilita může být rozhodující při stanovení únonosti přípoje. V takových případech poskytuje GMNA nižší únosnost než MNA. Nejběžnějším případem je spojitý sloup s velkou tlakovou silou zatížený také ohybovým momentem prostřednictvím rakově připojeného horizontálního nosníku. Ohybový moment způsobuje ve sloupu nestabilitu, která roste s rostoucím zatížením. Únosnosti může být dosaženo před dosažením 5% plastické deformace v deskách, přestože kritický násobek zatíčení z analýzy boulení je vysoký. Na obrázku níže je IPE 360 přivařena k HEA 200 a \(\alfa_{cr}=5,16\).
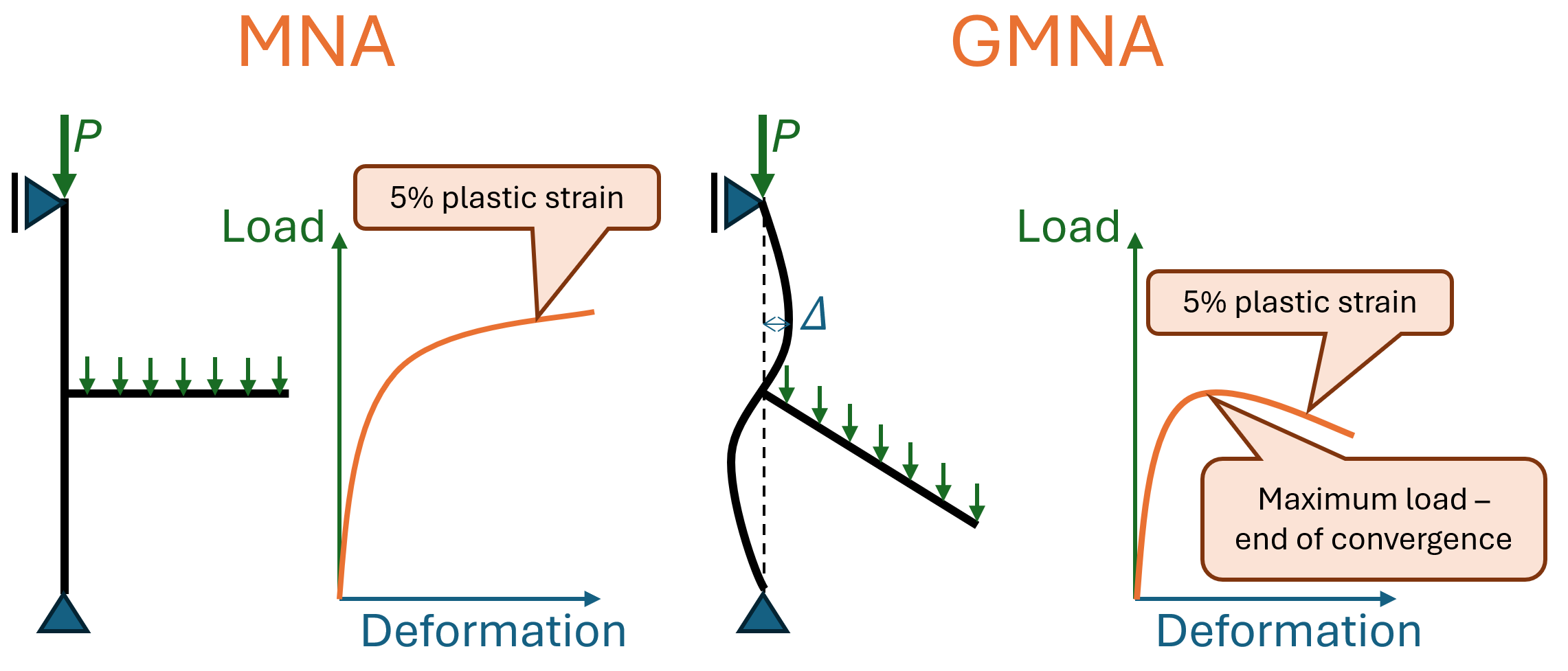
Únosnost stanovená pomocí GMNA je menší v důsledku takzvaných účinků druhého řádu. Tvar křivky zatížení-deformace stanovené pomocí MNA vždy je vždy rostoucí díky tvaru bilineárních pracovních diagramů oceli a komponent přípoje (šrouby, svary). Takže mezní únosnost je určena plastickou deformací nebo odolností komponet. Na druhou stranu křivka zatížení-deformace stavovená pomocí GMNA může také klesat v důsledku účinků druhého řádu. Pokud k tomu dojde před kritériem porušení plechů a komponent, je únosnost přípoje definována maximálním dosaženým zatížením. Viz. následující obrázek.
V těchto případech, které jsou poměrně časté, je skutečně nutné použít GMNA, abyste získali bezpečné výsledky. IDEA StatiCa a ISISE vedly společný projekt pro ověřování svařovaných momentových přípojů. Pro zkoumaný soubor 563 modelů s osovou silou ve sloupu rovnou 70 % plastické osové odolnosti sloupu \((0,7\cdot N_{pl,Rd})\) bylo průměrné snížení únosnosti při použití GMNA místo MNA 13,1 %. Maximální snížení bylo 19,8 %. Velikost této redukce únosnosti při použití GMNA se postupně snižuje s klesající tlakovou silou ve sloupu. Výsledky lze vidět v následující tabulce. Při nulové osové síle poskytují GMNA a MNA stejnou odolnost. V následující tabulce je snížení vypočteno jako \(M_{Rd,MNA} - M_{Rd,GMNA} -1\).
| Bez axiální síly | 30% \(N_{pl,Rd}\) | 50% \(N_{pl,Rd}\) | 70% \(N_{pl,Rd}\) | |
| Počet případů | 1380 | 619 | 606 | 563 |
| Průměrné snížení | 0.4% | 6% | 9% | 13.1% |
| Maximální snížení | 2.9% | 11% | 16.2% | 19.8% |
Doporučuje se použít GMNA pro případy s osovou tlakovou silou větší než 30 % \(N_{pl,Rd}\) spojitého sloupu (nebo pasu příhradové konstrukce).
Příklad zvýšené odolnosti
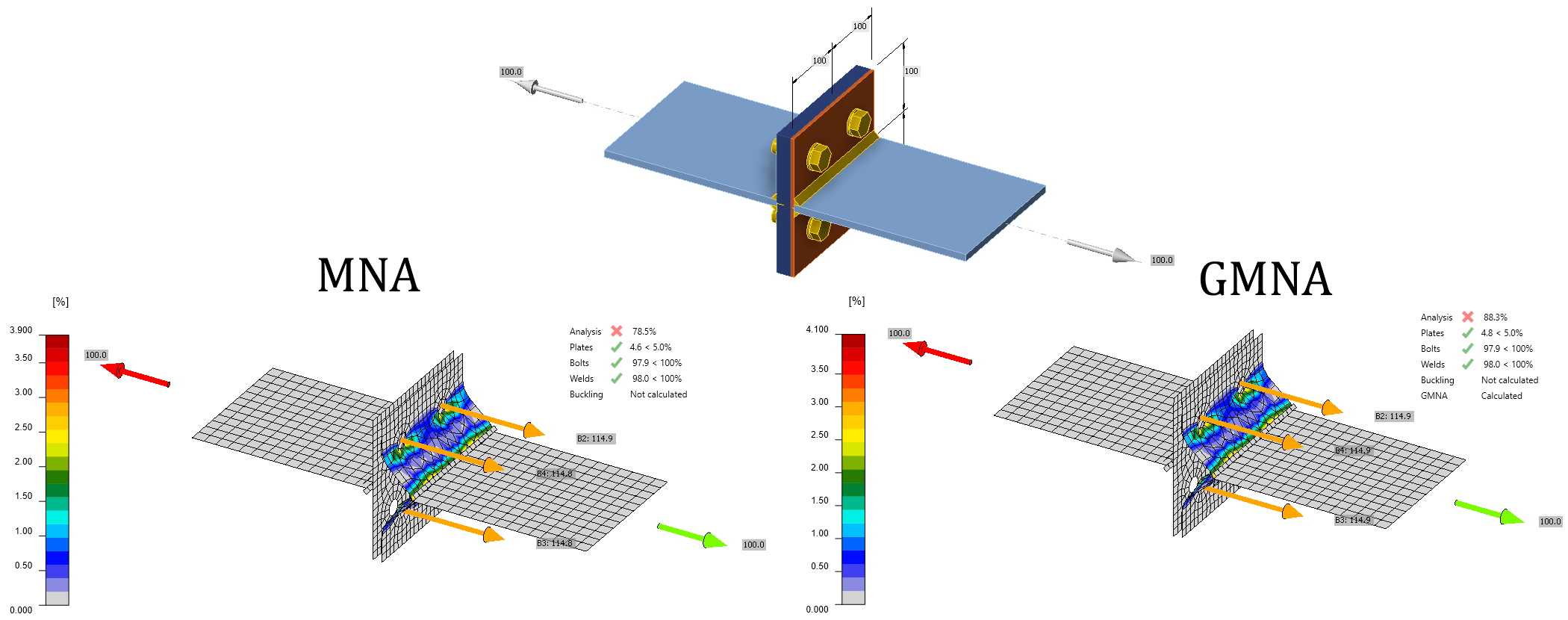
Příkladem, kdy GMNA může naopak poskytnout vyšší únosnost, je T-profil s tenkými deskami, kde se v analytickém řešení (komponentní metoda v Eurokódu nebo AISC) nezohledňují membránové síly. V následujícím příkladu jsou dva T-profily spojené zády k sobě. Jedna deska je výrazně tenčí - 5 mm oproti 20 mm. Tlustší z nich vytváří téměř tuhou podporu. GMNA poskytuje odolnost proti zatížení o 12,5 % vyšší než MNA. Všimněte si, že se jedná o extrémní případ a obvykle budou výsledky téměř totožné. Všimněte si také, že se jedná o skutečné chování prokázané experimenty, které však není zohledněno v tradičních metodách navrhování.
ČASTO KLADENÉ OTÁZKY
Mějte na paměti, že geometricky nelineární analýza je pokročilejší a náročnější na solver programu. Může odhalit některé nepřesnosti ve vašem modelu a může vyžadovat více omezení, např. pečlivější výběr typu modelu prutu - nastavení okrajových podmínek.
Uživatelům doporučujeme, aby vyzkoušeli obě možnosti a sami se přesvědčili o vlivu geometrické nelinearity na výsledky.
Měli byste se obávat svých předchozích návrhů, které proběhly bez geometrické nelinearity? Pouze v případě, že tlaková síla byla opravdu extrémní. Využití sloupů je podle tohoto výzkumu na celkovém průměru 0,49 s rozmezím 0,12-0,72, přičemž do využití průřezů sloupů je zde uvažováno normálová síla i ohybový moment. Uvedený mezní příklad 70 % \(N_{pl,Rd}\) je tedy stěží v praxi proveditelný.
Všimněte si také, že vzorce Eurokódu nebo AISC nezohledňují pro komponentu sloupu Stěna ve smyku společné působení osové síly a smyku. A pro stěnu průřezu sloupu v tlaku a tahu se interakce uvažuje jen nedostatečně, jak je uvedeno v tomto článku. IDEA StatiCa tedy nebyla jediná, která tento problém nedostatečně řešila, a nyní jej IDEA StatiCa jako první řeší pomocí GMNA.