Prestressing in Detail - Pre-tensioned strands

Introduzione e presupposti

Innanzitutto, iniziamo con una breve descrizione del nostro software di progettazione del calcestruzzo. Questo articolo riguarda principalmente la progettazione del calcestruzzo precompresso nell'applicazione Detail, che è generalmente sviluppata per la progettazione di regioni di discontinuità o per la progettazione di elementi contenenti regioni di discontinuità, come aperture, estremità tagliate, ecc.

Per confrontare i risultati, utilizzeremo l'applicazione Beam il cui scopo, come si può intuire dal nome, è la progettazione di travi in calcestruzzo.

In secondo luogo, è necessario definire alcune ipotesi e restrizioni per comprendere meglio la progettazione di travi in cemento armato precompresso in dettaglio.

• L'analisi in funzione del tempo (TDA) non è implementata nell'applicazione Detail. Per contro, la TDA è implementata nell'applicazione Beam per la progettazione di travi in cemento armato precompresso.
• La TDA può essere simulata in Detail utilizzando il coefficiente di scorrimento e gli incrementi.
• I carichi di ritiro e di temperatura non sono implementati nel Dettaglio.
• Il calcestruzzo in tensione nel Dettaglio è escluso. Quindi, per il nostro confronto, dobbiamo avere una trave senza fessure. Naturalmente, lo stesso approccio può essere utilizzato in generale per le travi affette da fessure, ma i risultati non saranno gli stessi nella Trave perché in essa è previsto solo il calcolo lineare.

Incrementi

Prima di passare all'esempio, è necessario capire come funzionano gli incrementi per la progettazione del calcestruzzo precompresso nel Dettaglio.

Ci sono 3 tipi di carico che vengono applicati al modello in tre incrementi nell'applicazione Detail.

• precompressione - per l'incremento P
• Permanente - per l'incremento G
• Variabile - per l'incremento V

Se si crea una combinazione contenente casi di carico di tutti i tipi di carico, l'intera porzione del tipo di carico Precompressione sarà applicata al primo incremento P, l'intera porzione del tipo di carico Permanenti sarà applicata al secondo incremento G e l'intera porzione del tipo di carico Variable sarà applicata al terzo incremento V.

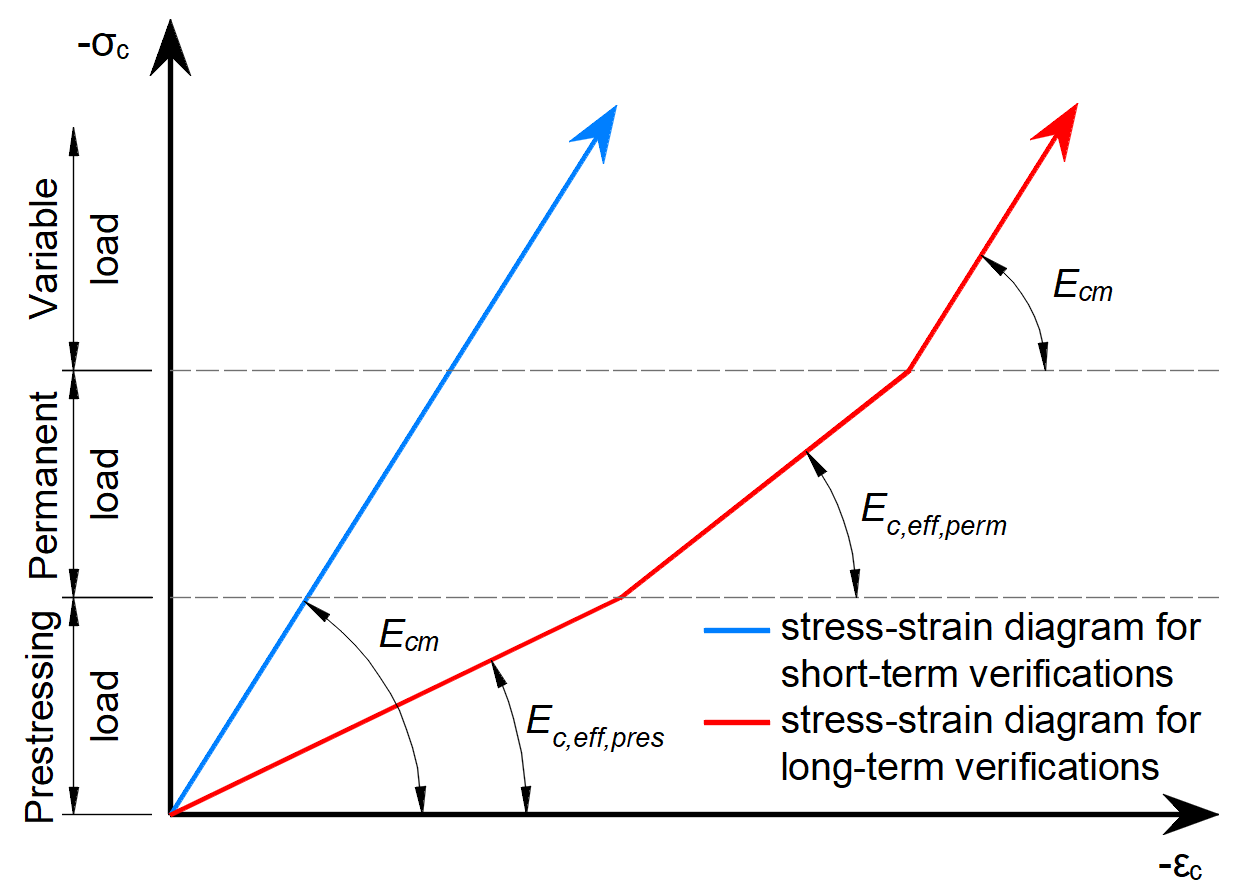
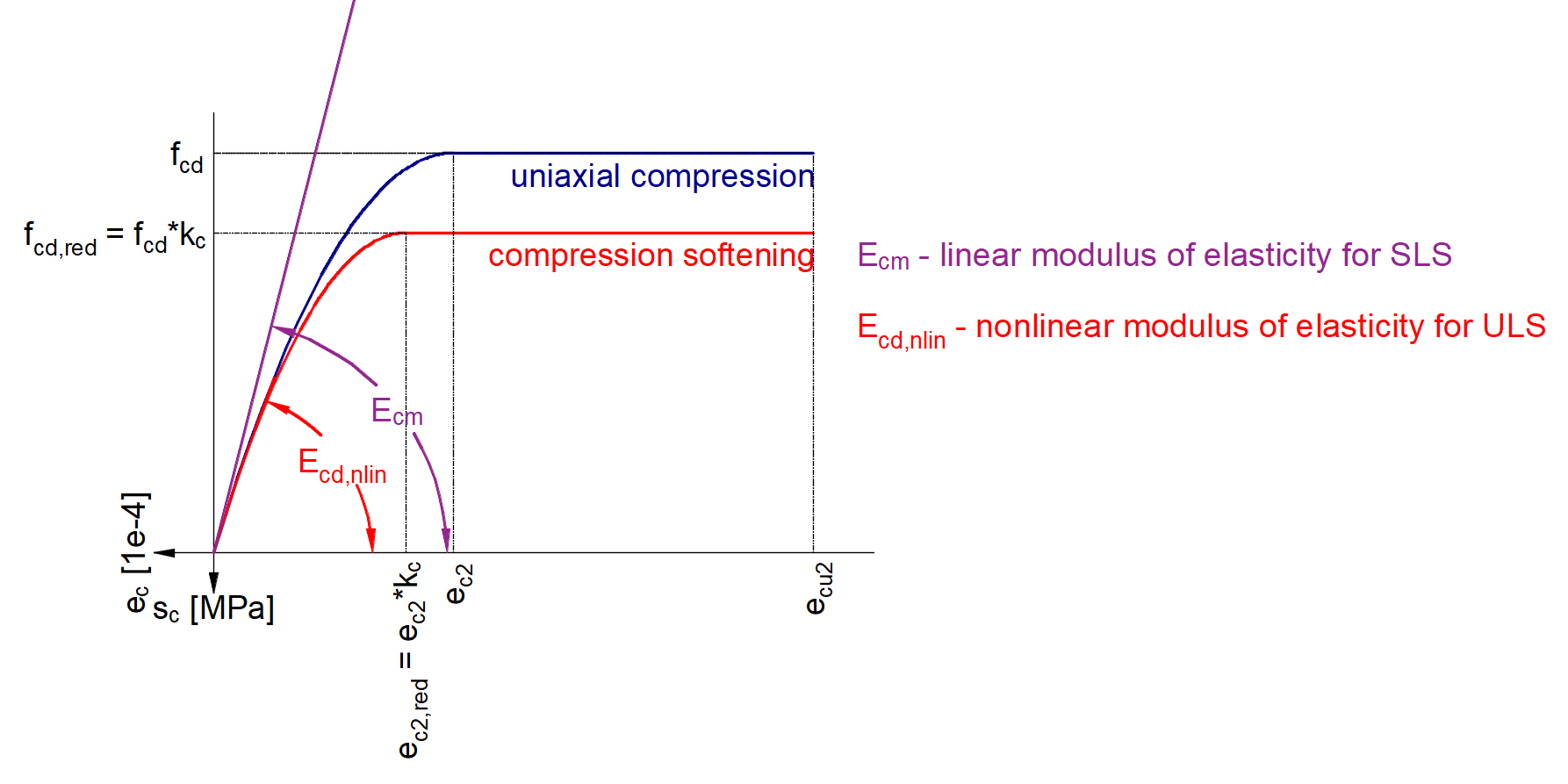
Il motivo per cui ci sono incrementi è che per i calcoli SLE vengono utilizzati diversi modelli di materiale (diversi moduli di elasticità), per SLU c'è un solo modello di materiale definito in Material model (EN).

Come si può vedere, ci sono tre moduli di elasticità:

• E_c,eff,press =E_cm / (1+φ_press) - Modulo di elasticità effettivo del calcestruzzo per l'incremento di P
• E_c,eff,perm =E_cm / (1+φ_perm) - Modulo di elasticità effettivo del calcestruzzo per l'incremento G
• E_cm - Modulo di elasticità secante del calcestruzzo

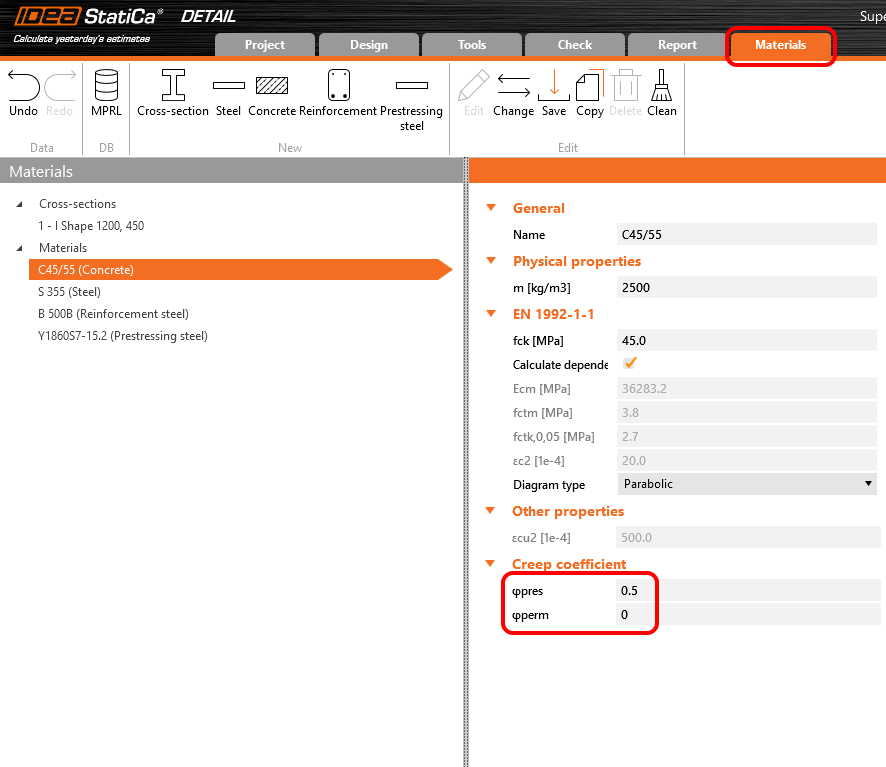
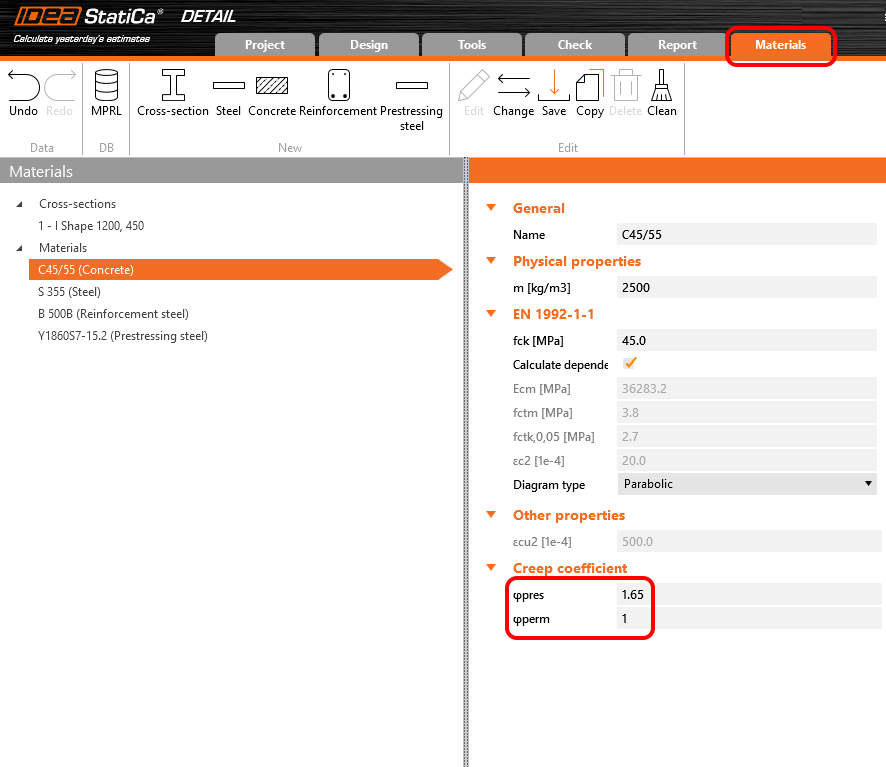
Dove φ_press e φ_perm sono i coefficienti di scorrimento per gli incrementi P e G. I coefficienti possono essere impostati in Materiali e modelli.

Si noti che per gli effetti a breve termine si utilizza solo E_cm . È valido per tutti e tre gli incrementi. La perdita a lungo termine viene presa in considerazione solo per gli effetti a lungo termine.

The beam parameters

Two identical models are created in the Beam and Detail applications. They are attached at the end of this article. Download them and go through them while reading the article. 

The example of a concrete beam will be introduced in the Beam application and then the comparison with Detail will be done for three construction stages.

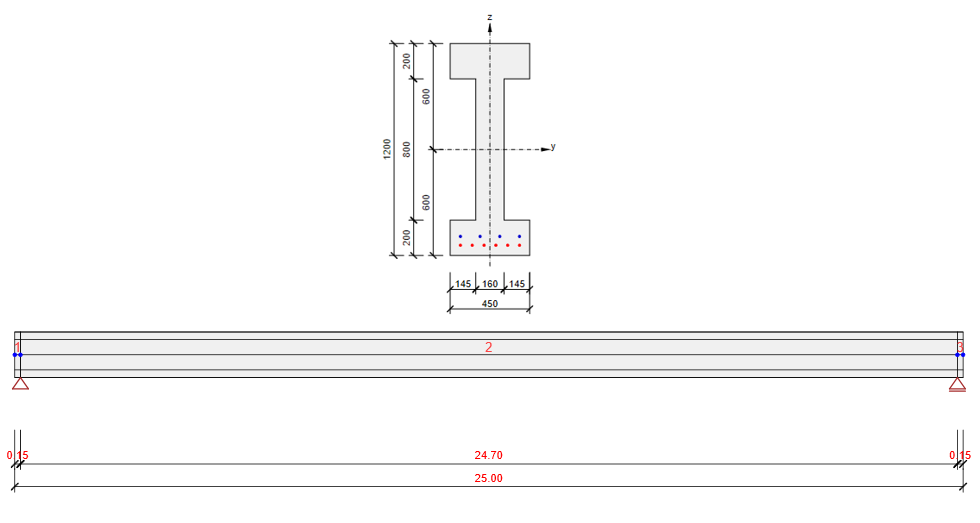
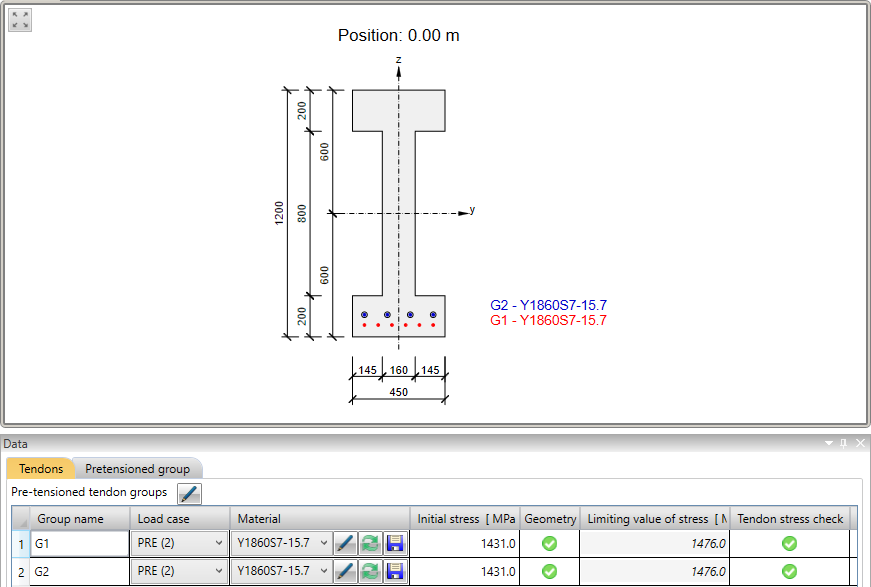
The example is a single span simple beam of I cross-section made of C45/50 concrete prestressed by pre-tensioned strands.

We will check the beam in three construction stages:

1. Transfer of prestressing - 2 d (just after release)
2. Superimposed dead load - 60 d (start of design working life)
3. End of design working life - 18250 d (50 years)

The other stages can be carried out similarly.

You will notice, that we used the user-specified concrete modulus. Read more in: How to input compressive strength value of concrete in construction stage?. That is because we want to show, how to model the beam which is prestressed before the concrete reaches the 28-day modulus of elasticity.

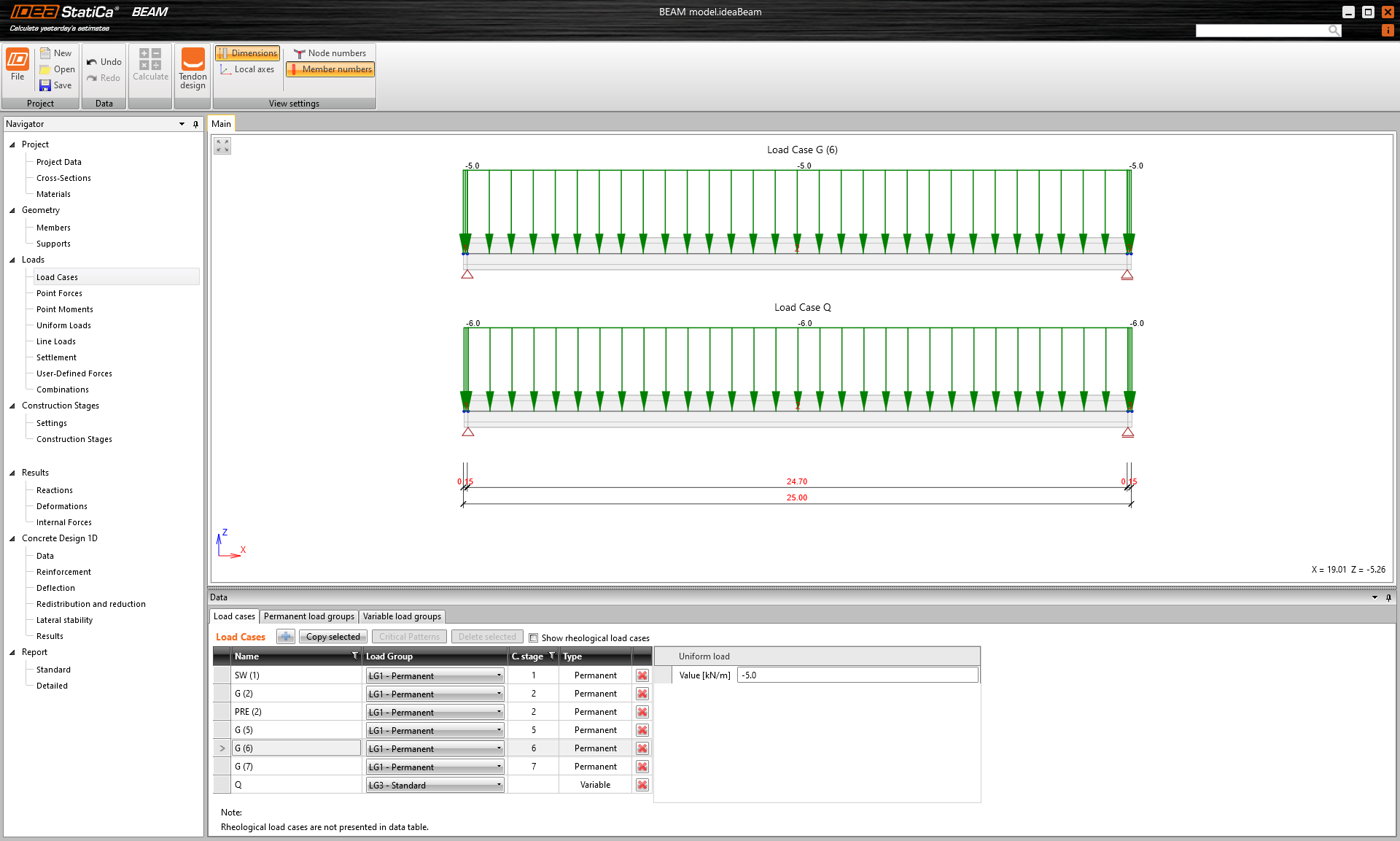
There are only four load cases input. The numbers in the brackets are the numbers of the construction stages where the individual loads are applied.

1. Self-weight - SW (1)
2. Prestressing - PRE (2)
3. Permanent load - G (6)
4. Variable load - Q

Other load cases are empty.

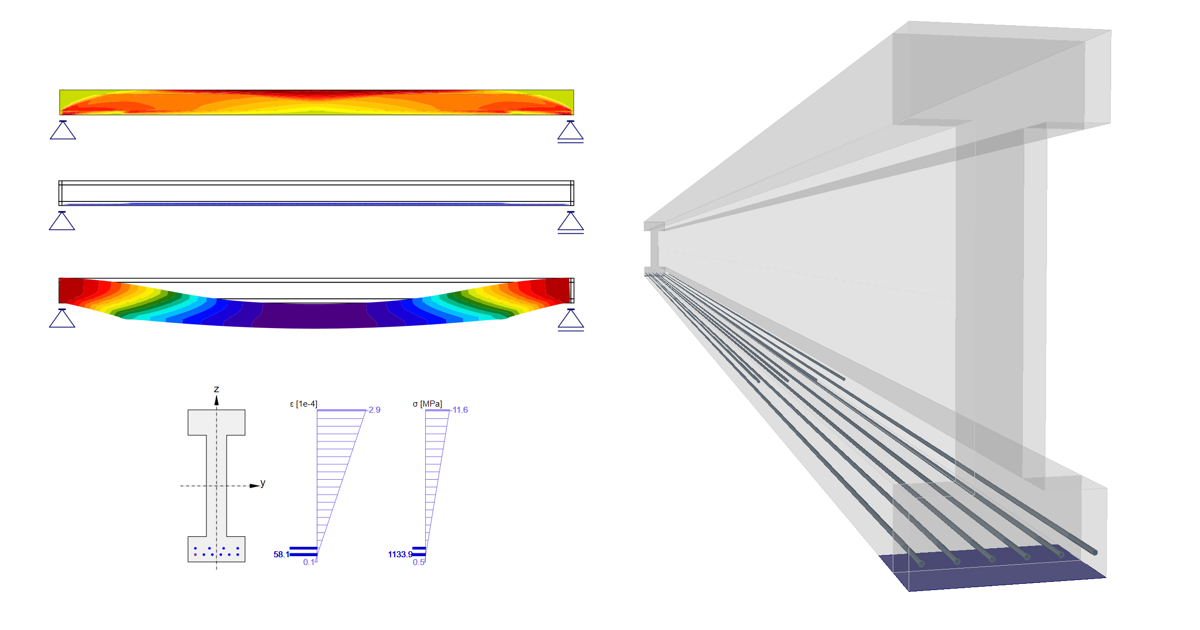
Now let's take a look at the prestressing. There are two rows of strands. It is worth mentioning, that the upper row has a blanketed length 3.0 m.

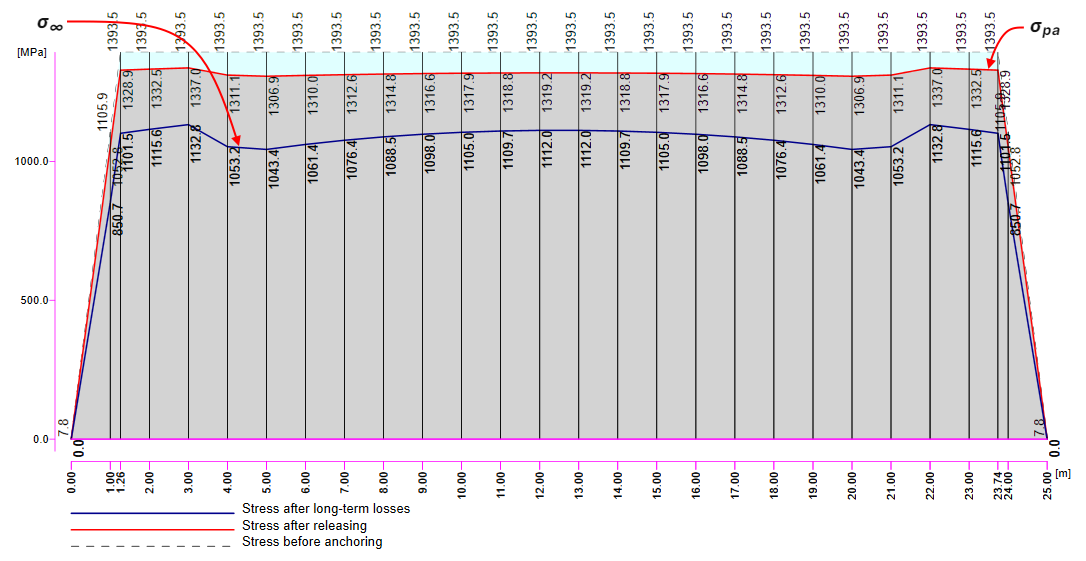
In the next figure, you can see the Tendon Stress/Losses chart. 

There are several values of stress in the tendon that should be controlled during the prestressing application. At this point, we will stop and briefly explain the prestressing process and individual stresses and losses. 

Prestressing process for pre-tensioned beam

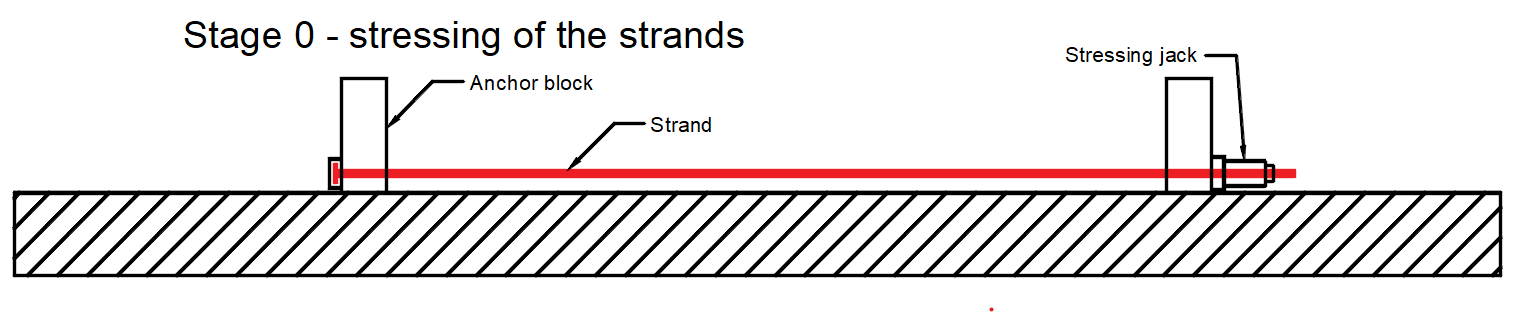
Stage 0 - stressing of strands -> The strands are prepared to their position, anchored on one side and prestressed by stressing jack on the other site. 

• σ_p,ini - Initial stress - maximum stress during tensioning. It has to be lesser than σ_p,max according to EN 1992-1-1 5.10.2.1. It is stress on the stressing jack. In our example σ_p,ini = 1431 MPa.

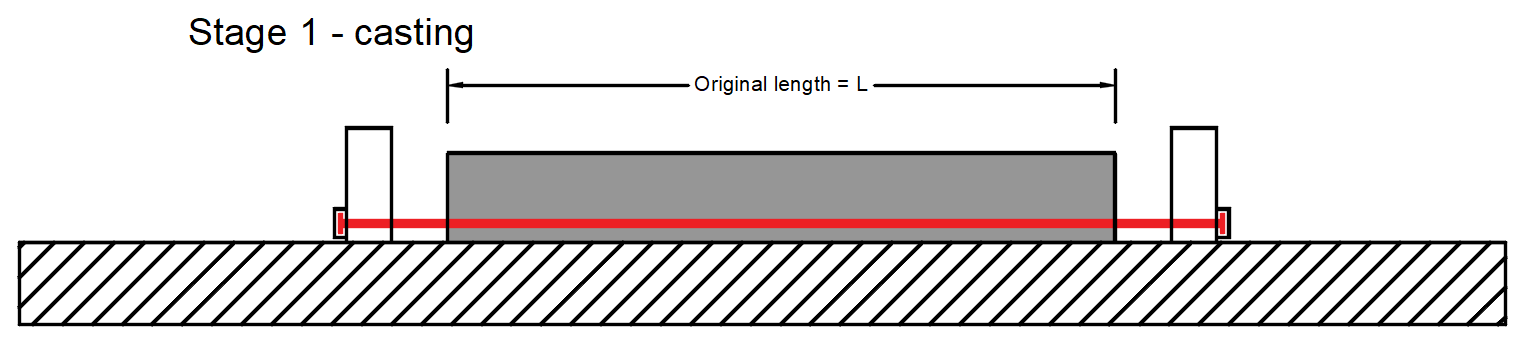
Stage 1 - casting -> The concrete member is being cast around the prestressed tendons in this stage. 

• σ_pr,cor - Stress after short-term relaxation that also includes anchorage set loss and loss due to the deformation of abutments. In our example σ_pr,cor = 1415 MPa 

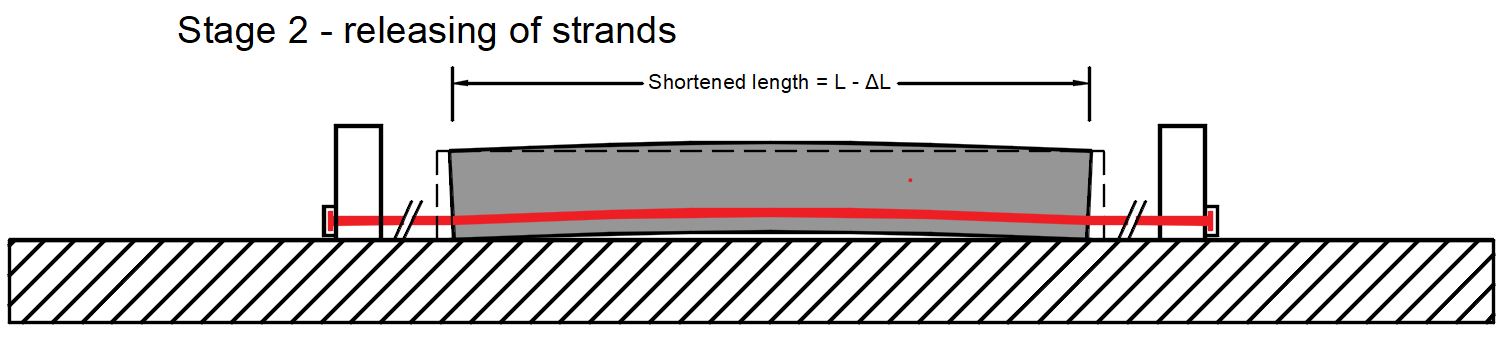
Stage 2 - releasing of strands -> The strands are released and the immediate elastic concrete strain is realized.

• Δσ_pT - Loss due to difference of temperature of prestressing steel and stressing bed.
• σ_pm0 - Stress just before release - This value is the input to the Detail. It is also the stress before the loss due to immediate elastic concrete strain - Δσ_pe. It is calculated as σ_pm0 = σ_pr,cor - Δσ_pT. In our example σ_pm0 = 1386 MPa
• Δσ_pe - Loss due to immediate elastic concrete strain.
• σ_pa - Stress after short-term losses. In other words, it is a stress after the transfer of prestressing to the member. It is calculated as σ_pa = σ_pr,cor - Δσ_pT - Δσ_pe = σ_pm0 - Δσ_pe. In our example σ_pa = 1319.2 MPa

Stage 3 - end of working life

• σ_∞ - Stress after long-term losses

Now recall the figure above (with the Tendon Stress/Losses chart) where the values of σ_pa (red line) and σ_∞ (blue line) are displayed.

• Read more: Prestressing in Detail - Model description

Transfer of prestressing stage

The model is defined, so let's switch to the Detail application and have a look at how to set the first stage. The model is the same, we only added stirrups for shear transfer, but it will not influence the results.

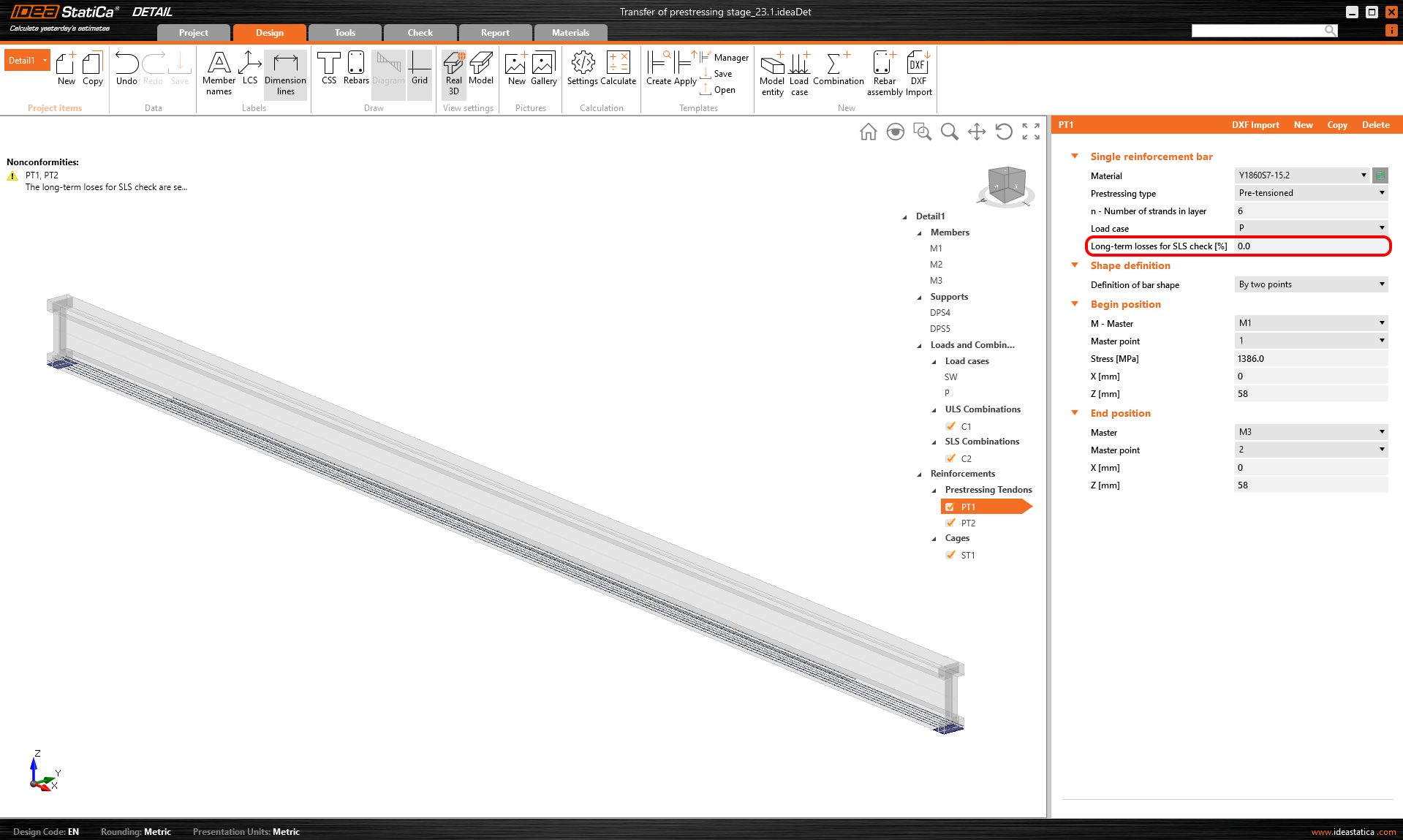
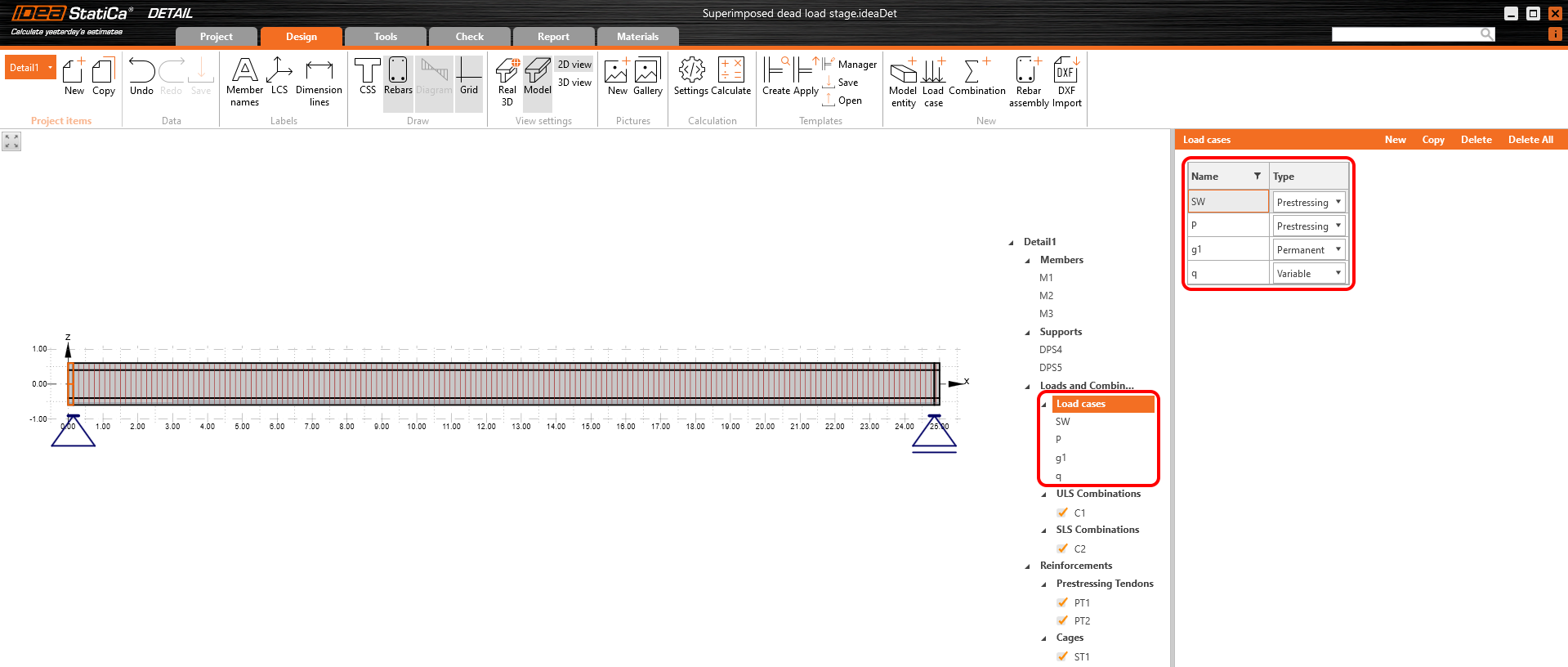
For this stage, there are only two load cases:

1. SW - Prestressing type (Self-weight)
2. P - Prestressing type (Prestressing)

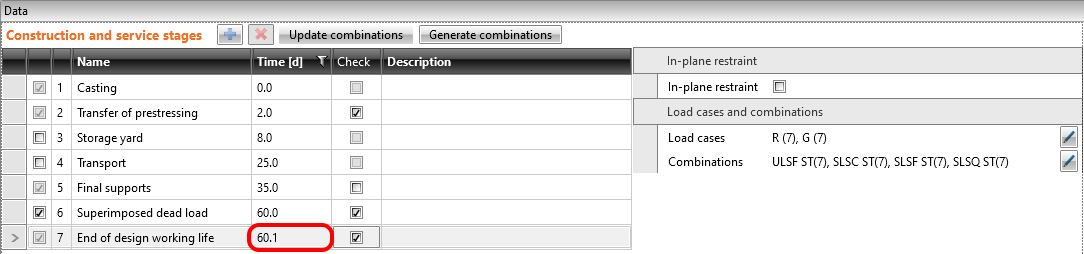
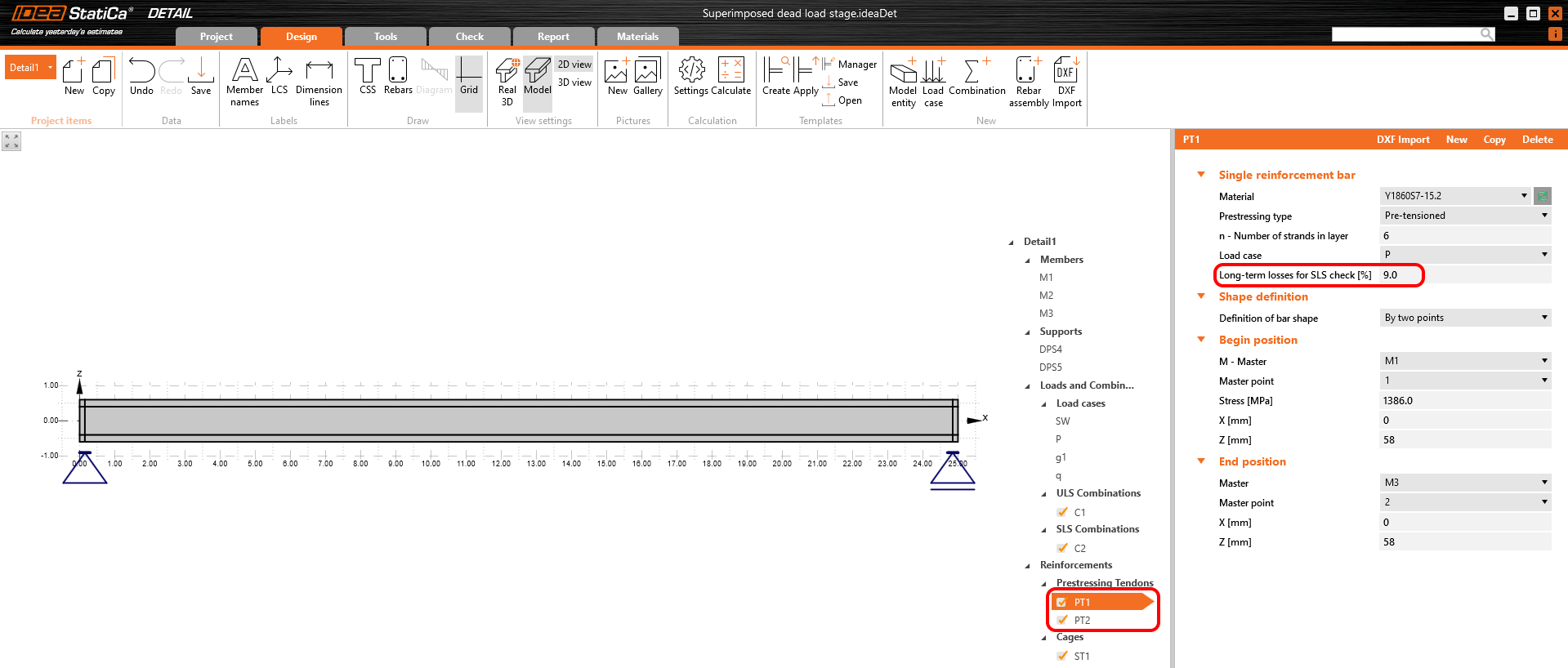
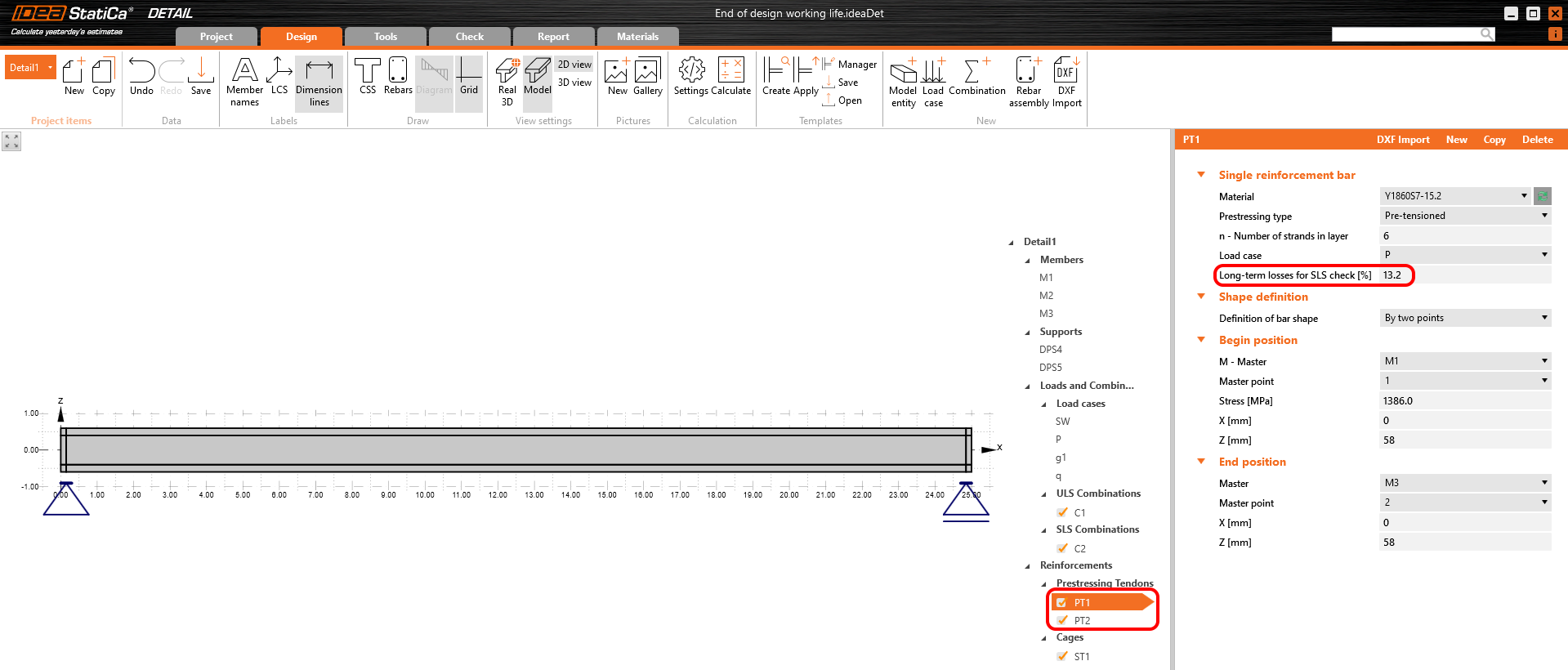
Both of them will be applied in the first load increment. Long-term losses for SLS checks are set to 0% as you can see.

• Read more: General description of Load impulses in Detail application

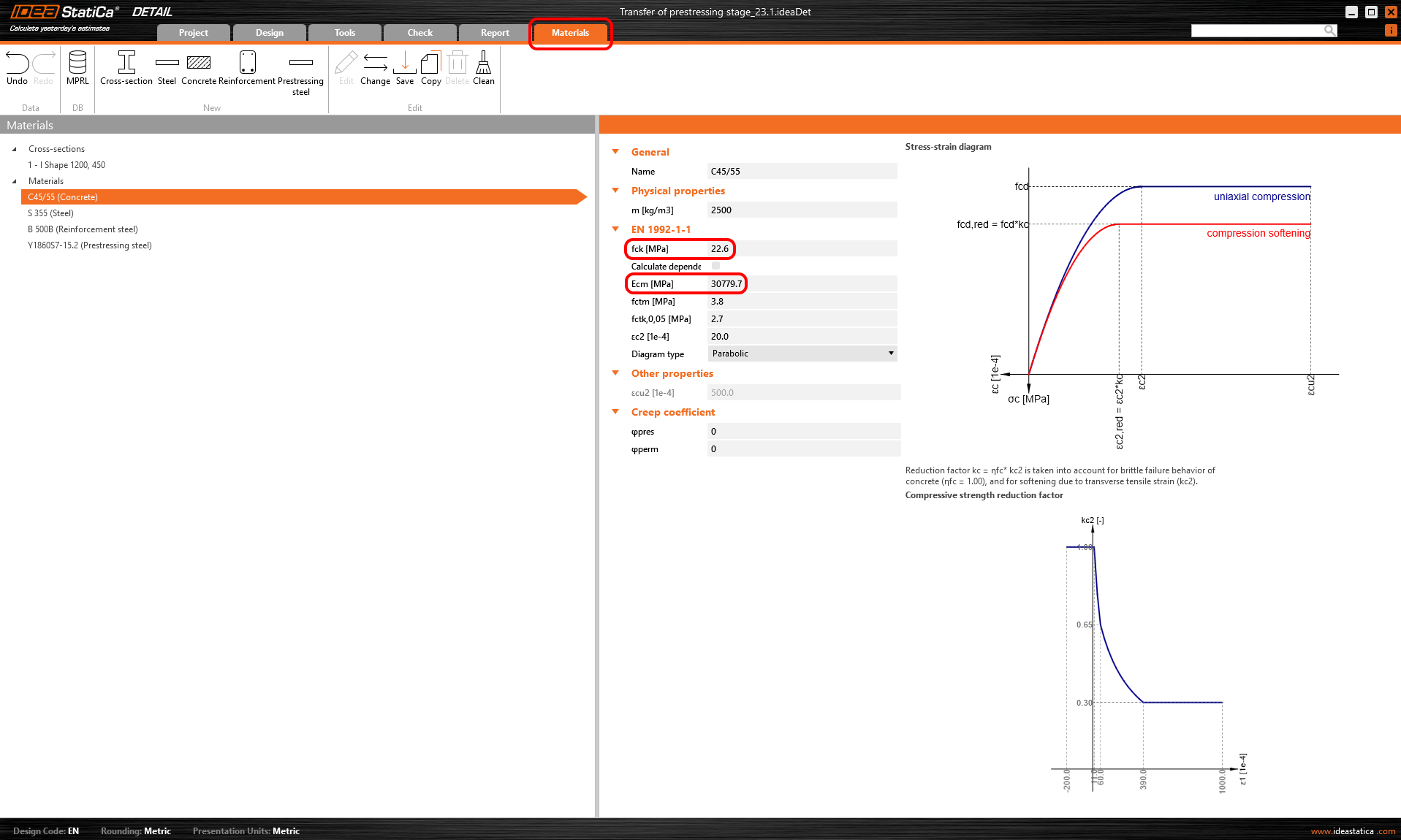
Creep coefficients are also set to zero value because we want to assess the stage just after the transfer of prestressing. And, you can see that the value of E_cm was rewritten to the same value we input into the Beam application.

So let's compare the results. Because we didn't input any creep factor or long-term loss, the long-term and short-term effects are the same. 

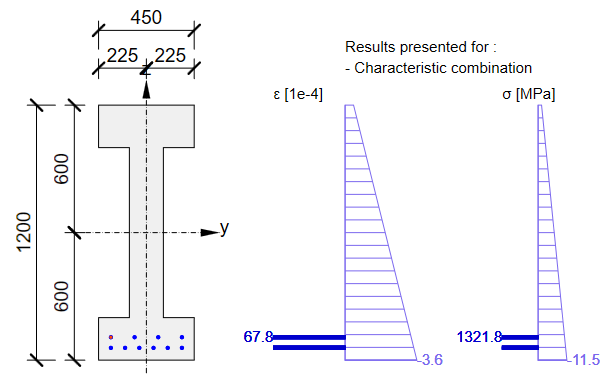
Stress in tendons in SLS:

Stress in concrete in SLS:

• Read more: General description of SLS results in Detail application

The SLS section check from Beam:

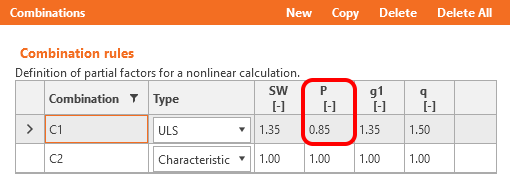
As you can see there is a good match. So it seems we have done the input for this stage correctly. Note that the coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) was set as 1.0 in the Beam application.

On the other hand, for the ULS check, we can expect a significant difference between the Beam and Detail applications results. It will be caused by the loss due to immediate elastic concrete strain - Δσ_pe, which is calculated differently in Beam (linear approach) and in Detail (CSFM).

• In the linear approach (Beam application), loss due to immediate elastic concrete strain Δσ_pe is the same for ULS and SLS. The reason is that in the case of the linear approach, we use the linear material model with the modulus of elasticity E_cm, calculated from f_ck, for the whole analysis (also for the analytical calculation of losses) and only for ULS cross-sectional checks, we use the material model where the modulus of elasticity is calculated from f_cd. 
• In the Detail application approach, the whole ULS is calculated with the material model where the modulus of elasticity is calculated from f_cd (also influenced by η_fc factor, see Material models (EN)). It causes greater elastic strain and consequently greater loss Δσ_pe. Please recall that we input the stress before loss due to immediate elastic concrete strain. This loss is calculated based on the strain of the model affected by prestressing forces (in the case of ULS with the lower modulus of elasticity).

Note that SLS is calculated in the Detail application based on E_cm (not based on f_ck). On the other hand, ULS is calculated based on f_cd from which the parabolic stress-strain diagram is determined. 

• Read more: General description of ULS results in Detail application

Now you know how to use the Detail application for the design of prestressed concrete structures using pre-tensioned tendons for the transfer of prestressing stage. Just change the geometry and add some discontinuities like openings etc. 

Superimposed dead load stage

The time (age of the concrete) for this stage is 60 days. The purpose of this stage is to check the concrete beam at the start of its working life including permanent and variable loads. So the other two load cases are added. Load impulses are of course the same as in the Beam application model.

We need to determine two values as input for Detail. 

1. Creep coefficient for the time from 2 days to 60 days
2. Estimation of long-term losses for the time from 2 days to 60 days

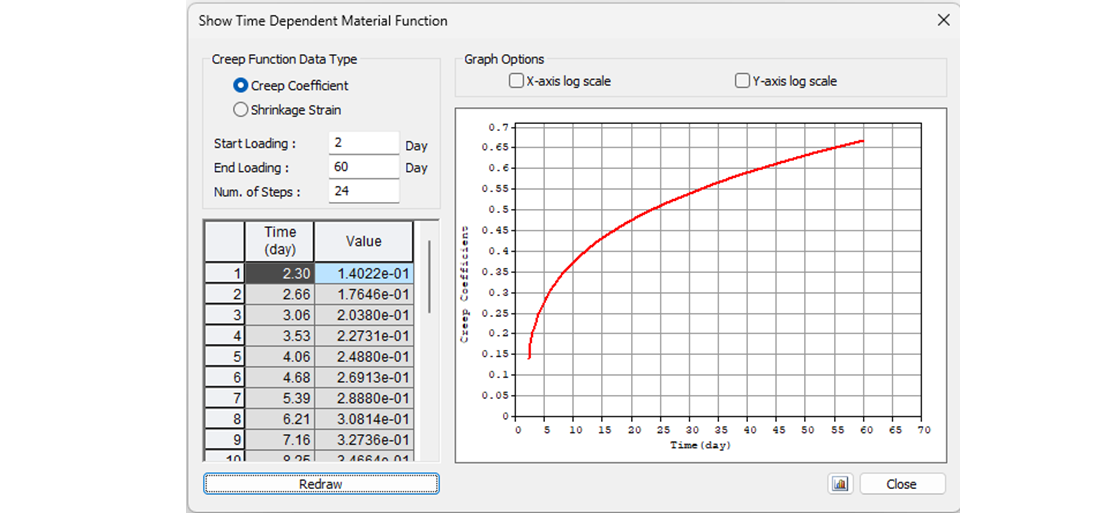
Let's start with the creep coefficient. In the following figure, you can see the creep function from 2 to 60 days for concrete grade C45/55 and cement class R according to the Eurocode. The value of the creep coefficient is then φ_pres ≈ φ₍₆₀₎ - φ₍₂₎ = 0.65 - 0.15 =  0.50

In the Detail application, the creep coefficient can be set in Materials & models. It is obvious that the modulus of elasticity has to be set as the default E_cm value (recall the Increment chapter and the chart in it). You will also notice that the value of φ_perm = 0.0, which is because we want to apply permanent loads as short-time loads as well as variable loads.

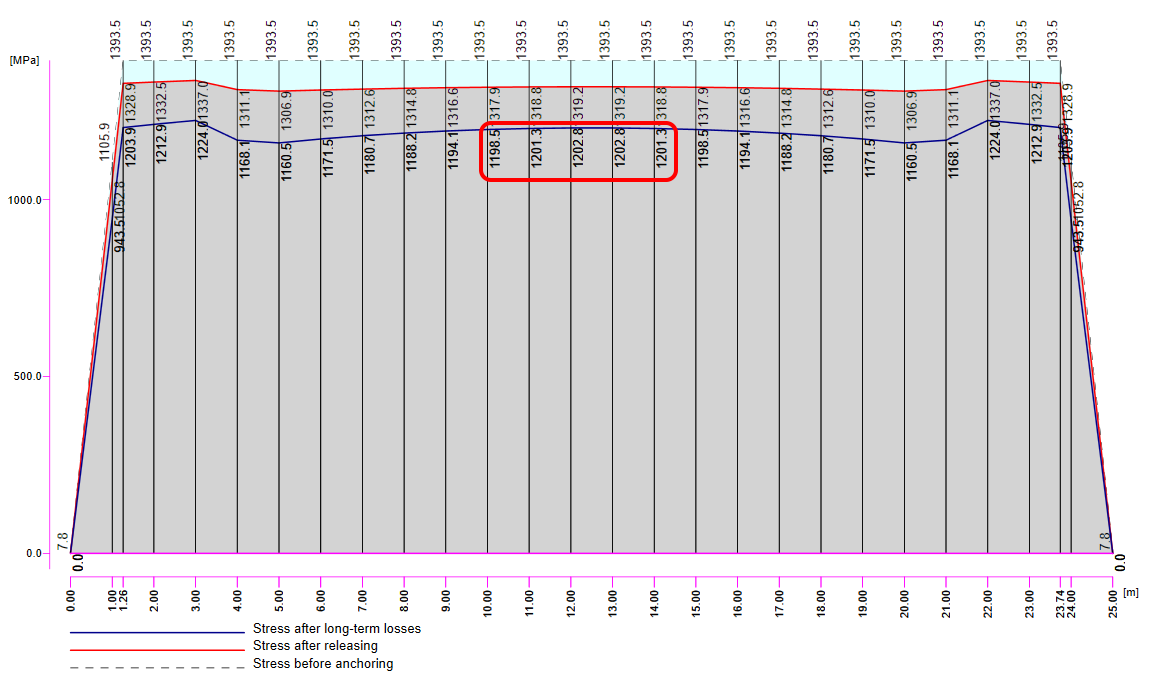
Now it is time for the long-term losses. Of course, you can estimate them (my estimation would be 10%). It is the easiest way, but in our example, we want to do it precisely. So we calculated σ₆₀ - Stress after long-term losses in 60 days (blue line) in the Beam application by setting the final time to 60 days.

The value of σ₆₀ = 1200 MPa as can be seen in the following figure (blue line).

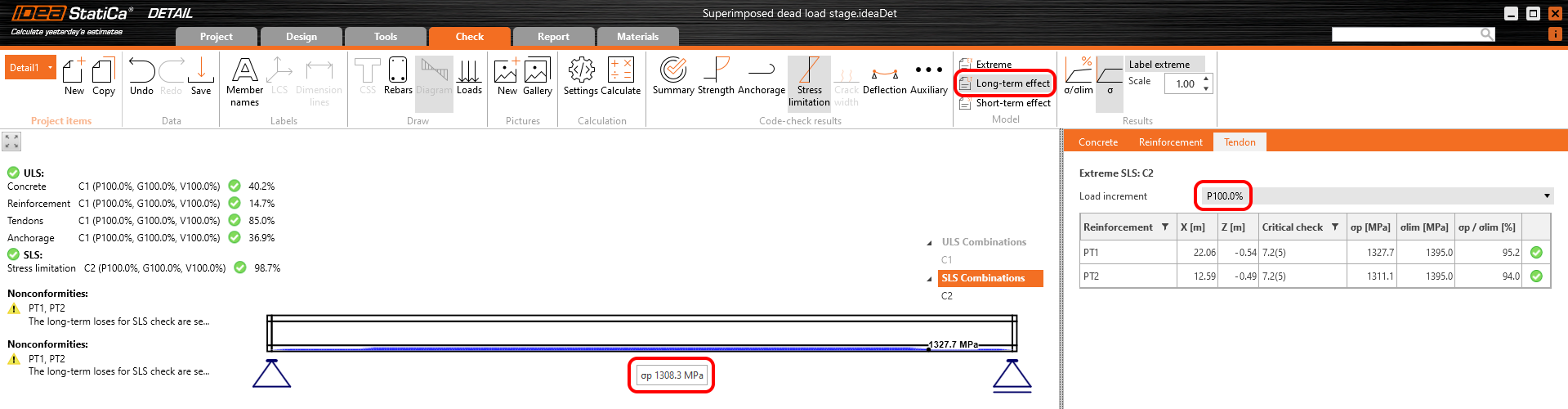
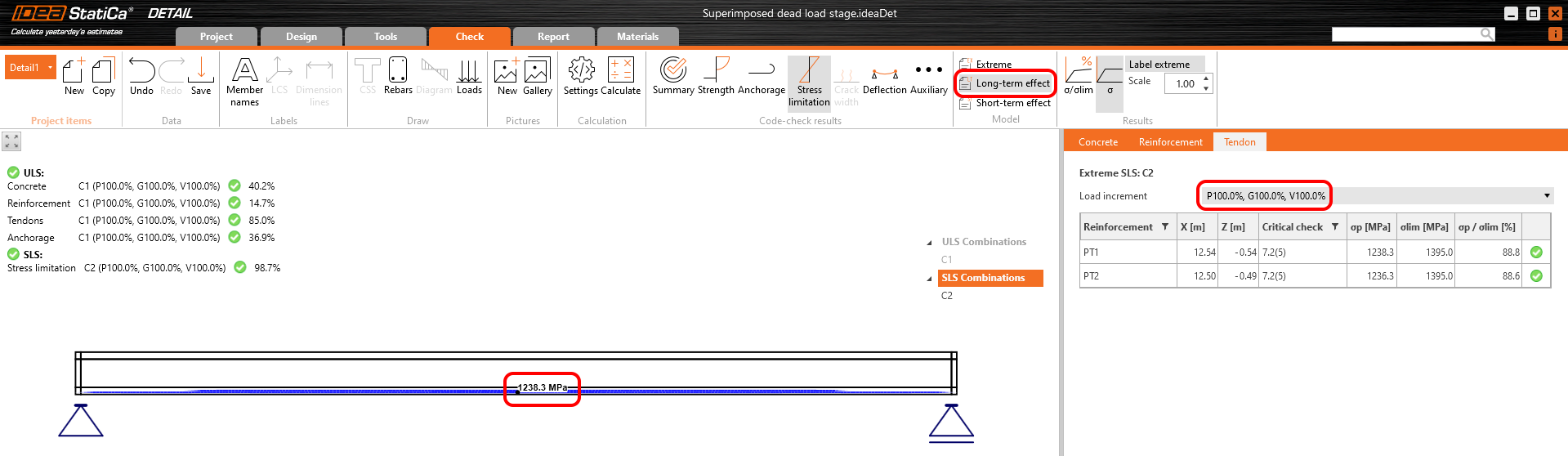
Then we need to calculate the model in the Detail application with the creep coefficient set and with zero long-term losses for the first increment - P100% to determine σ_det,60. The important thing is that we need to read the results for long-term effects to have the creep coefficient included.

In the figure, we can see that σ_det,60 = 1308.5 MPa.

The long-term losses can then be calculated as σ₆₀ / σ_det,60 = 1200 / 1308.5 = 0.91 -> long-term loss is 9%. Let's input the value and compare the results.

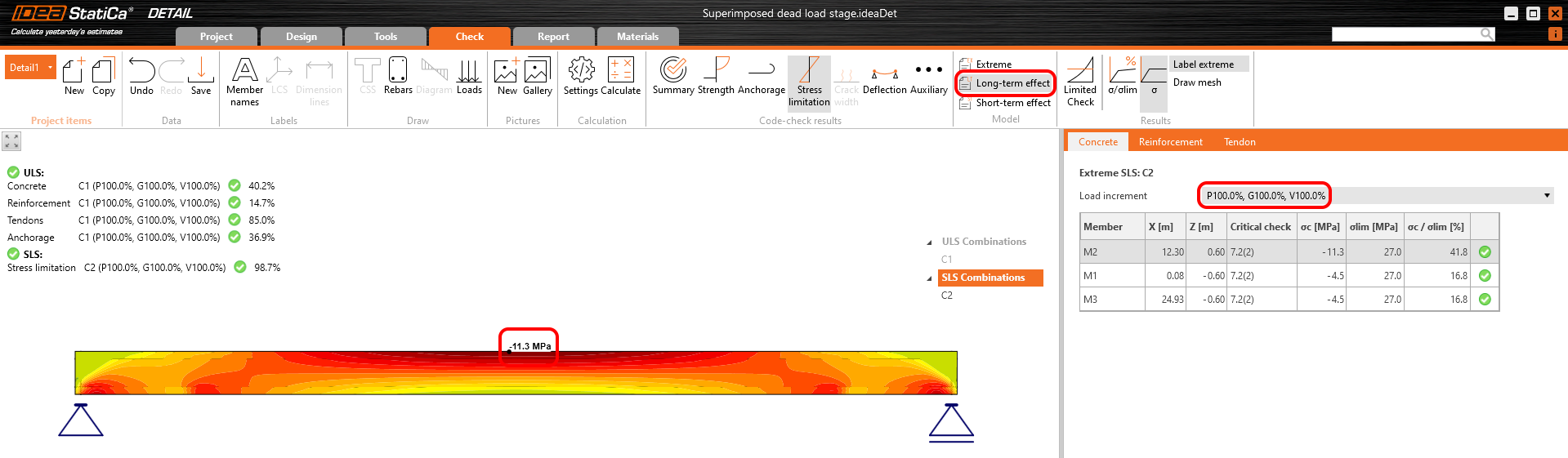
The results are read for long-term losses (we want to have creep and losses included) and for all increments (we want to have all loads included). 

Stress in tendons in SLS:

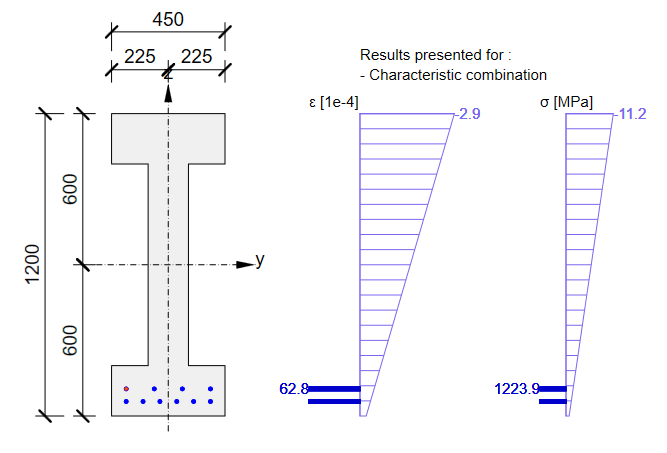
Stress in concrete in SLS:

The SLS section check from the Beam application:

Again, there is a good match. So, it seems we have done the input for this stage correctly. For ULS there will be the same issue described in the previous stage. Note that the coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) was set as 1.0 in the Beam application.

Now recall the beginning of this article where the increments were described. In the Detail application model for this stage, you can go through the individual increments to see the influence of individual load cases. You can also check the short-term effects which will differ from the previous Detail application model for the transfer of prestressing stage. The reason is the different modulus of elasticity E_cm used in these models. 

What you can actually see in the model for the superimposed dead load stage in short-term effects is a transfer of prestressing stage where t=28 days. So, if you don't need to prestress the beam before 28 days you don't need to create a special model for the design of prestressed concrete beams in the transfer of prestressing stage.

End of design working life

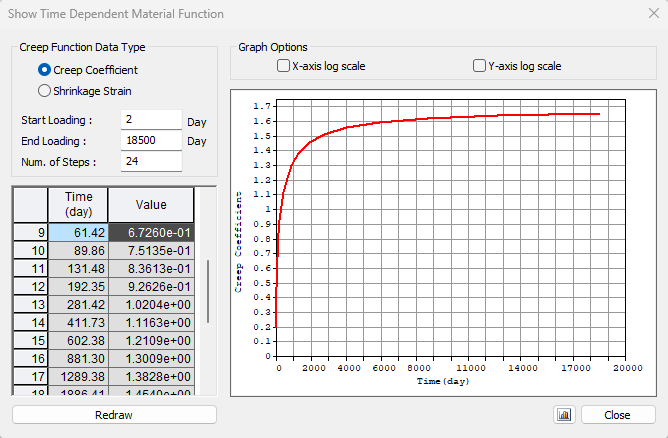
The approach will be the same as for the previous stage. First, we need to determine creep coefficients. In the following figure, you can see the creep coefficient function. 

The value φ_pres ≈ 1.65 for the time from 2 to 18250 days for cement class R according to the Eurocode. The value φ_perm = φ_(18250) - φ₍₆₀₎ ≈ 1.65 - 0.65 = 1.00 for the time from 60 to 18250 days. Note the highlighted value φ₍₆₀₎ in the table above. 

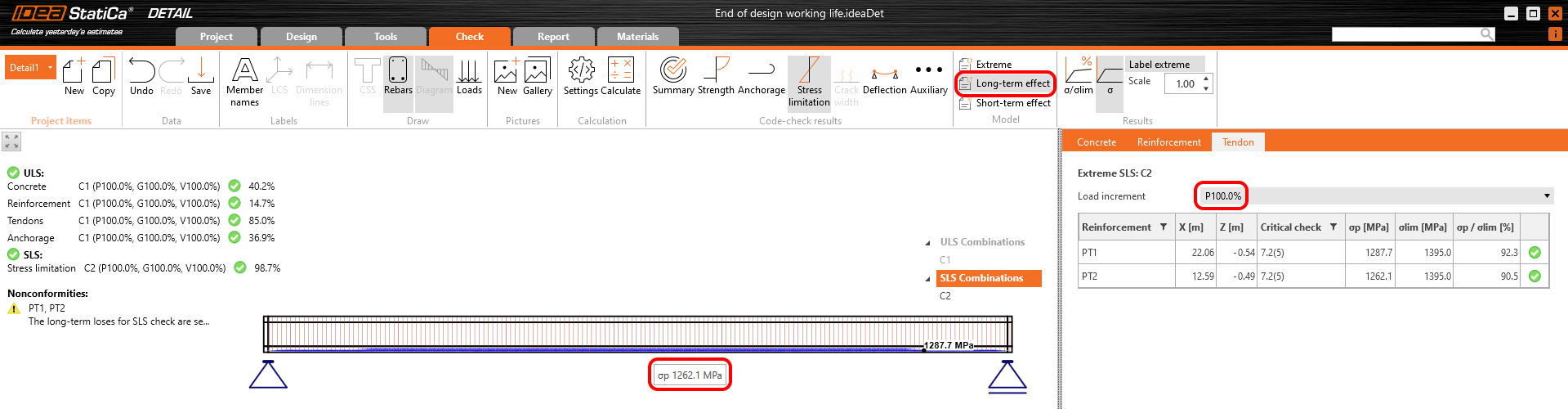
Secondly, we need long-term losses. Again, we used the same approach, we calculated the model in the Detail application with the creep coefficients set and with zero long-term losses for the first increment - P100%. The important thing is that we need to read the results for long-term losses to have the creep coefficient included.

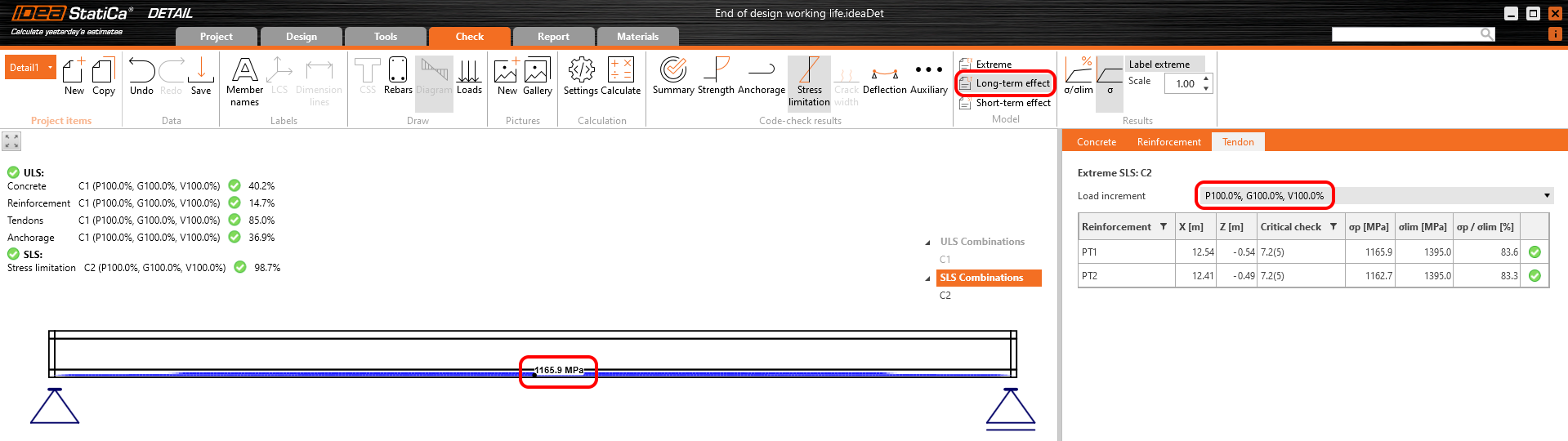
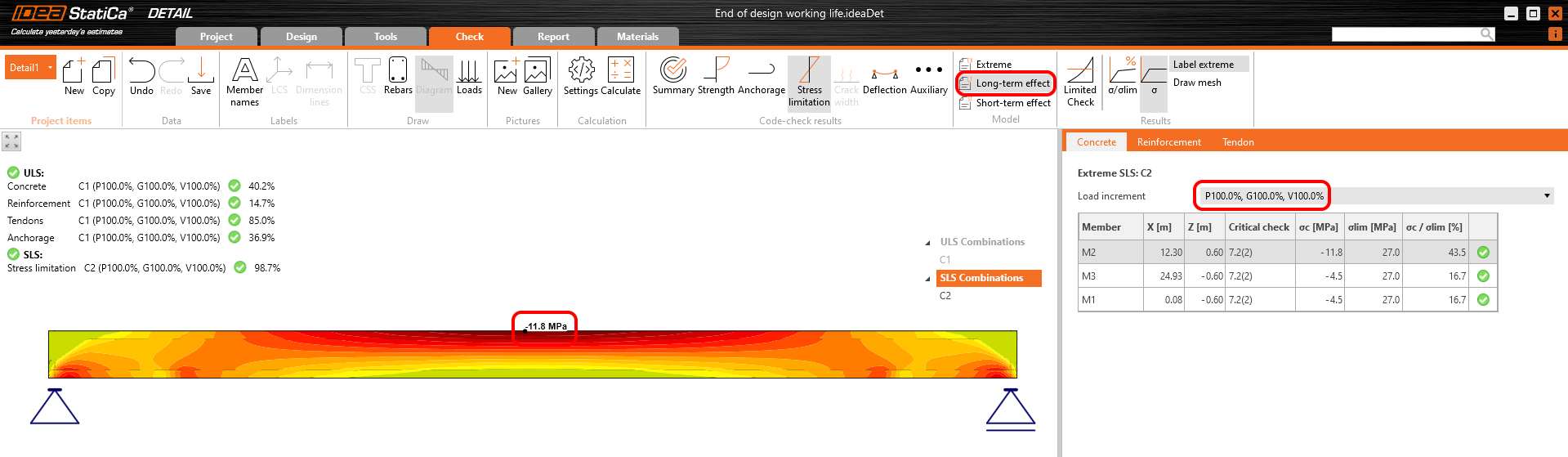
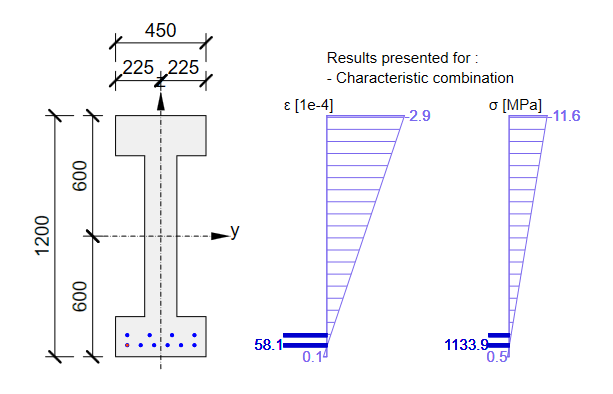
The long-term losses can be calculated as σ_∞ / σ_det,∞ = 1100 / 1267 = 0.868 -> long-term loss is 13.2%. The value of σ_∞ is determined in The beam parameters chapter in the Tendon Stress/Losses chart. Let's input the value and compare the results.

Stress in tendons in SLS:

Stress in concrete in SLS:

The SLS section check from Beam:

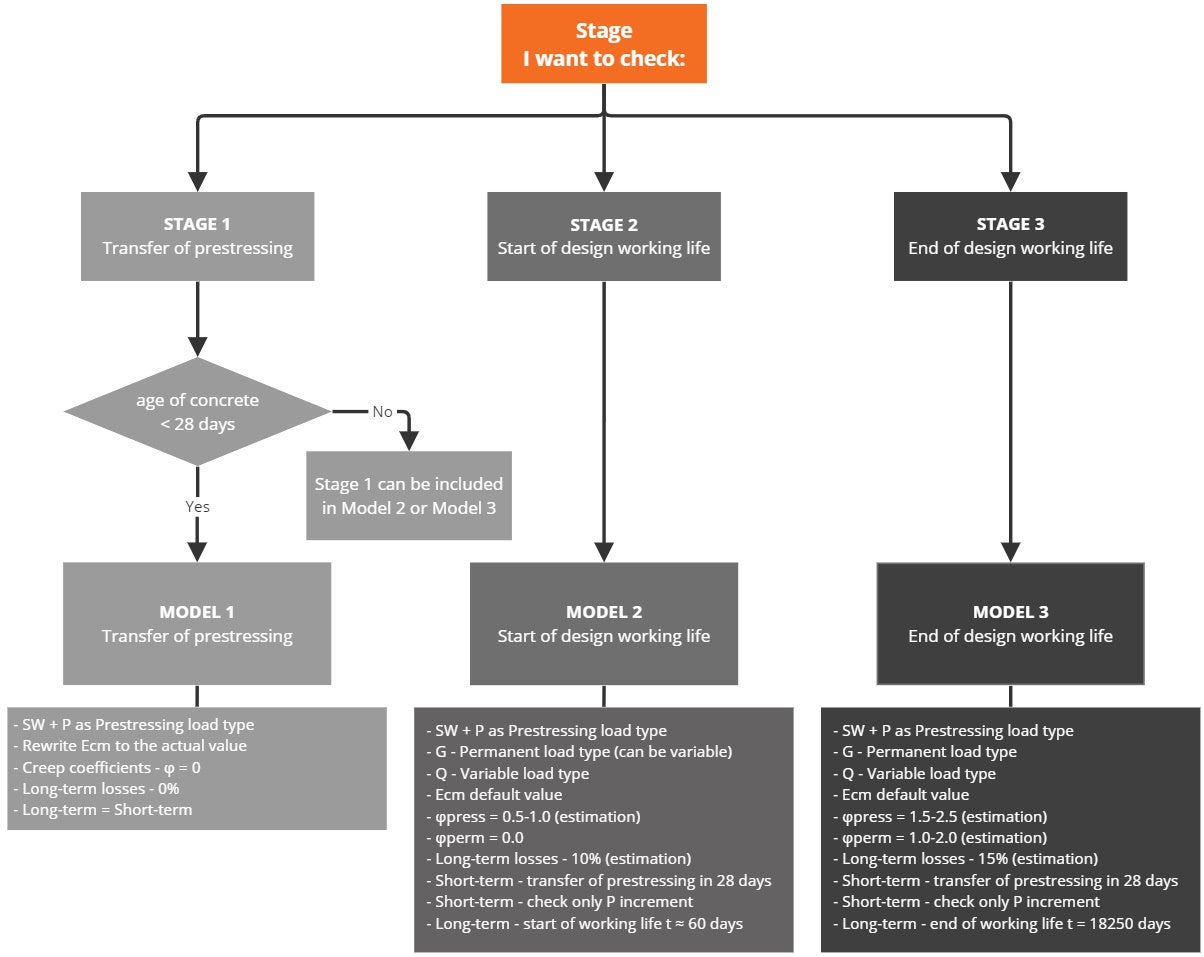
Conclusion

Finally, here is a simple workflow, where you can find the above-described procedure of designing the prestressed concrete structures in the Detail application using pre-tensioned tendons.

It's worth repeating that for pre-tensioned strands the stress just after release (but before the loss due to immediate elastic concrete strain) has to be input. An estimate of the long-term losses due to shrinkage and relaxation should be input. Creep losses are calculated automatically.

It follows from the preceding that for Model 2 and Model 3 for short-term effects, only the first increment P needs to be considered (since no other permanent loads, nor variable loads will be applied during applying prestressing). It is valid only if the age of concrete when applying prestressing is greater than 28 days, otherwise, you have to do a special model for Stage 1 (for short-term effects).

Long-term losses for ULS have to be set as a combination factor. The estimation of long-term losses which can be set in reinforcement is taken into account only for SLS checks. The input for the estimation of 15% should look like this:

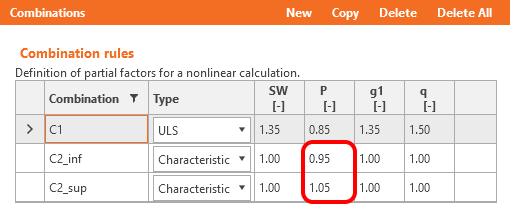
Coefficients r_inf and r_sup defined in EN 1992-1-1; 5.10.9 (1) for prestressing effects for SLS should be also taken into account in combinations. It means you should create at least two combinations. See the figure.

Read about the implementation of these coefficients in the Beam application in How the r_inf and r_sup coefficients are taken into account for SLS checks

You have read how to use IDEA StatiCa Detail a concrete design software where you can, among other things, do a design of prestressed concrete beams with discontinuities. But let's not forget about the IDEA StatiCa Beam, which is used for concrete beam design including TDA, and which we used for comparing the results.

Download allegati

• BEAM model.ideaBeam (IDEABEAM, 959 kB)
• Transfer of prestressing stage.ideaDet (IDEADET, 13 kB)
• Superimposed dead load stage.ideaDet (IDEADET, 15 kB)
• End of design working life.ideaDet (IDEADET, 15 kB)