Distribuzione della forza del bullone nella connessione trave-colonna con piastra di estremità

In questo articolo discutiamo la distribuzione delle forze del bullone e i fattori che la influenzano. Determinare l'effettiva distribuzione delle forze in un giunto è spesso impossibile. Ciò richiede una comprensione del comportamento del giunto e la conoscenza delle diverse rigidezze e deformazioni. IDEA StatiCa Connection aiuta a comprendere questi effetti. Confrontiamo i risultati di IDEA StatiCa con un calcolo manuale per una distribuzione lineare e mostriamo perché la distribuzione reale delle forze è quasi sempre non lineare.

Formato

Potremmo parlare di infinite situazioni, ma in questo esempio ci limiteremo a una connessione trave-colonna con piastra di estremità, bulloni 2x5 M16 8.8 e un momento flettente puro sulla trave. Le saldature sono modellate come saldature di testa e non verranno discusse.

Nei prossimi 5 punti si discuterà di come vari fattori influenzino la distribuzione della forza dei bulloni.

1 - Centro di rotazione libero

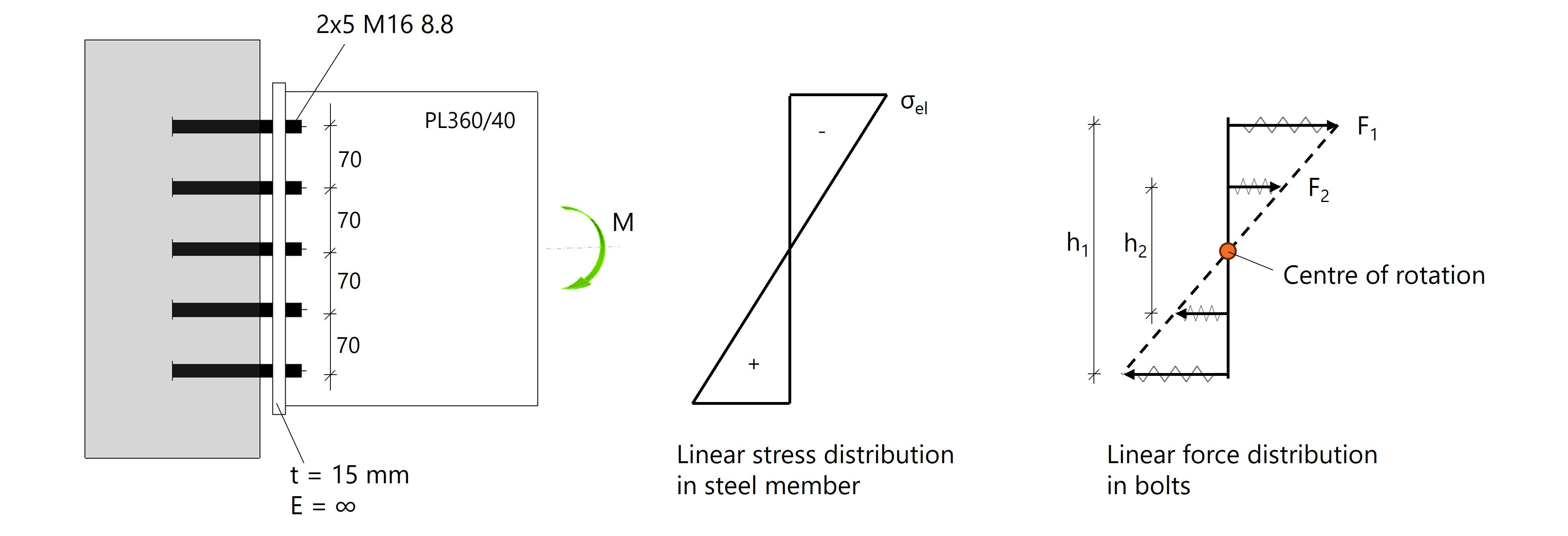
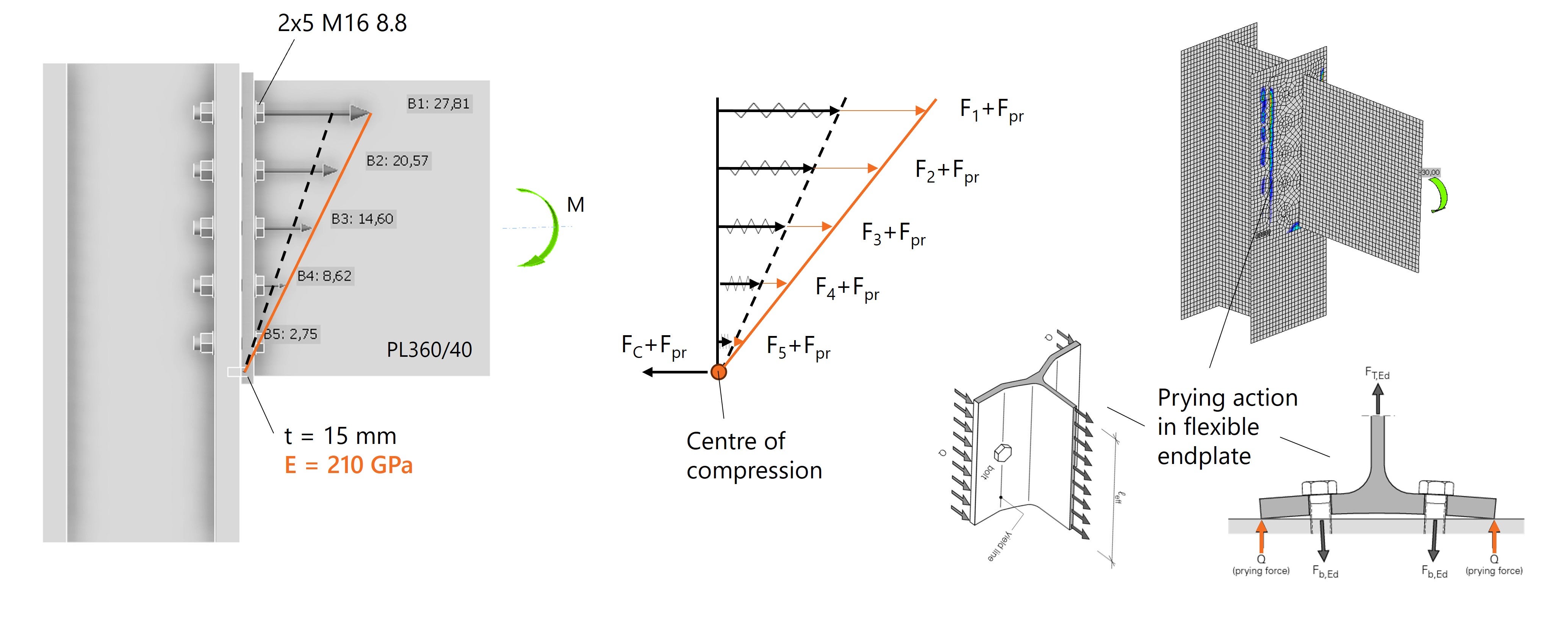
Cominciamo con un esempio teorico in cui la trave è modellata come una piastra PL360/40. Il momento flettente che agisce sulla trave crea una distribuzione elastica lineare delle sollecitazioni, con l'asse neutro esattamente al centro. Queste sollecitazioni si traducono in una corrispondente distribuzione di forze dei bulloni, ma solo quando le rigidezze sono simmetriche, i bulloni possono trasferire anche forze di compressione e il comportamento rimane completamente elastico.

Per approssimare questo aspetto, nella situazione 1 abbiamo modellato il giunto come una piastra di base infinitamente rigida (E=∞) con ancoraggi e un gap. Il giunto si comporta allo stesso modo in trazione e in compressione, creando un punto di rotazione ideale situato a metà della fila di bulloni.

Fig. 1: La distribuzione delle sollecitazioni nella trave è uguale alla distribuzione delle forze nei bulloni a causa della rotazione libera.

Possiamo verificare la distribuzione lineare delle forze con un calcolo manuale. Se F_i rappresenta la forza in un bullone, si ottiene il seguente equilibrio:

\( M = 2F_1 \cdot h_1 + 2F_2 \cdot h_2 \).

Poiché le distanze tra i bulloni sono uguali, si ottiene:

\( F_2 = \frac{1}{2} \cdot F_1 \).

Il momento flettente in tutti gli esempi è M = 30 kNm.

Se lo completiamo, possiamo calcolare F₁ e F₂:

\( M = 2F_1 \cdot h_1 + F_1 \cdot h_2 = 2F_1 \cdot 0,28 + F_1 \cdot 0,14 = 0,70 F_1 = 30 \) kNm

\( F_1 = 30 / 0,70 = 42,86 \) kN (per bullone)

\( F_2 = F_1 / 2 = 42,86 / 2 = 21,43 \) kN (per bullone)

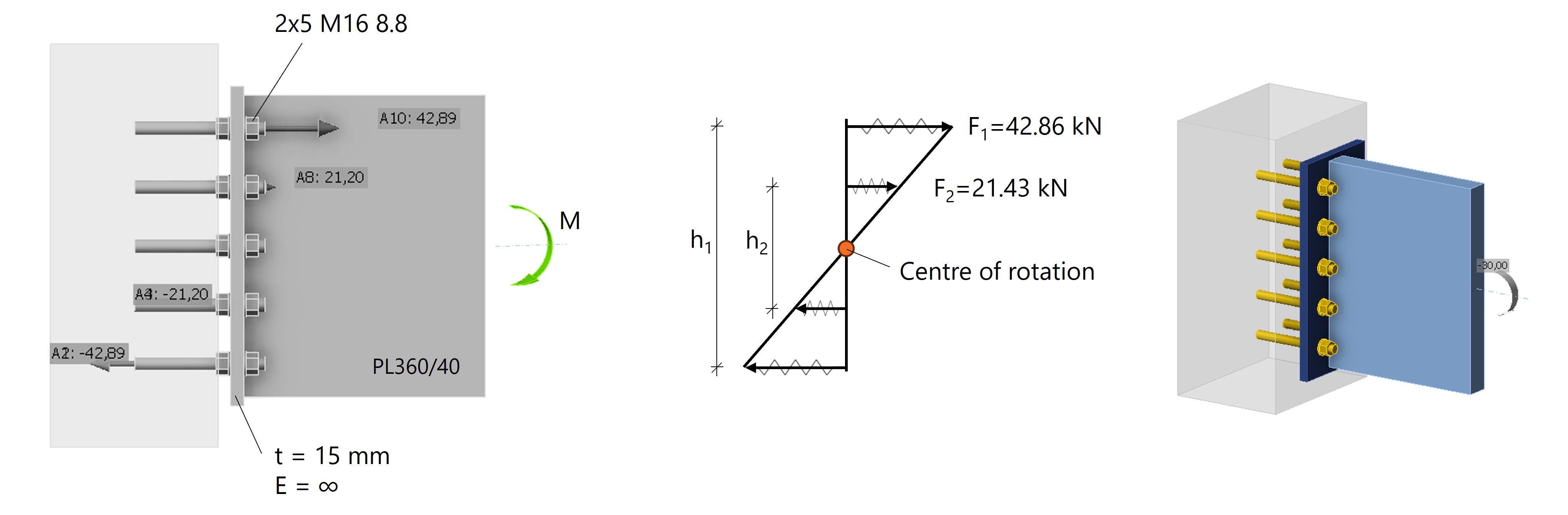
I risultati per F₁ e F₂ sono stati confrontati con le forze calcolate per i bulloni in IDEA StatiCa. Di seguito vediamo che le forze nei bulloni sono quasi uguali.

Fig. 2: Distribuzione lineare della forza dei bulloni in IDEA StatiCa modellando i bulloni come ancoraggi.

*Nota: per confrontare il calcolo CBFEM con il calcolo manuale, dobbiamo assumere una piastra di estremità infinitamente rigida e modellare la trave come una piastra PL360/40 invece che come un profilo a I. Più avanti vedremo perché questo è importante.

2 - Centro di rotazione forzato

In una connessione realistica con piastra di estremità, i bulloni non trasferiscono forze di compressione e la compressione viene trasmessa attraverso il contatto tra la piastra di estremità e l'ala della colonna. Si verifica una variazione delle rigidezze che causa lo spostamento del centro di rotazione, ora chiamato centro di compressione, verso il basso.

Per confrontare correttamente i calcoli manuali, abbiamo modellato una striscia stretta alla base della piastra di estremità, in modo che il centro di compressione sia sempre alla base della piastra di estremità.

Inoltre, la trave è stata modellata come una piastra e abbiamo aumentato il modulo E delle parti in acciaio per limitare le deformazioni. In questo modo si ottiene una distribuzione perfettamente lineare delle forze del bullone con il centro di rotazione alla base della piastra di estremità.

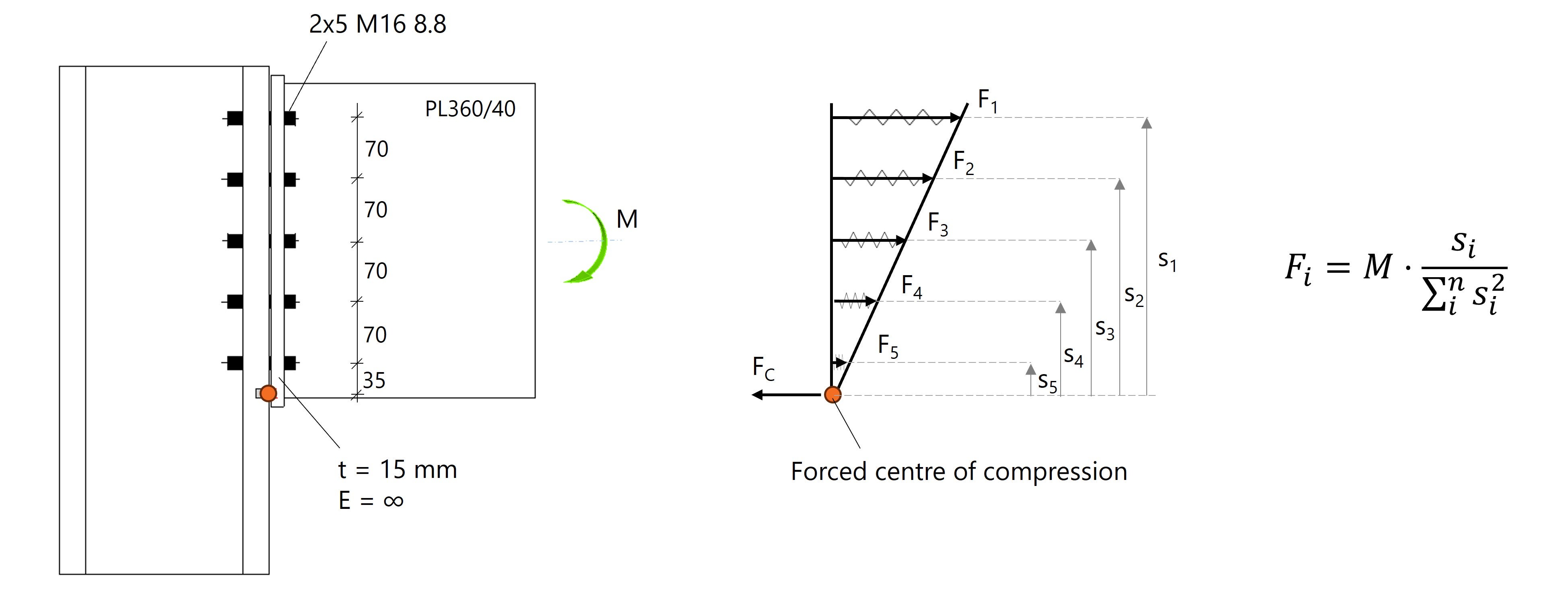
Fig. 3: Distribuzione lineare delle forze dei bulloni con il centro di rotazione (compressione) alla base della piastra di estremità.

Sulla base delle distanze e dei carichi noti, le forze dei bulloni vengono calcolate con la seguente equazione:

\( F_i = M \cdot \frac{s_i}{\sum_{i}^{n} s_i^{2}} \).

Ogni fila di bulloni ha 2 bulloni e si assume che le forze siano uguali. Per la fila di bulloni 1, otteniamo:

\( 2F_1 = M \cdot \frac{s_1}{\sum_{i}^{n} s_i^{2}} = 30 \cdot \frac{0,315}{(0,315^2+0,245^2+0,175^2+0,105^2+0,035^2)} \} = 46,75 \) kN

Questo dà \( F_1 = 46,75/2 = 23,37 \) kN

In questo modo, possiamo calcolare la forza di un bullone per fila:

• \( F_1 = 23,37 \) kN
• \( F_2 = 18,18 \) kN
• \( F_3 = 12,98 \) kN.
• \( F_4 = 7,79 \) kN
• \( F_5 = 2,59 \) kN

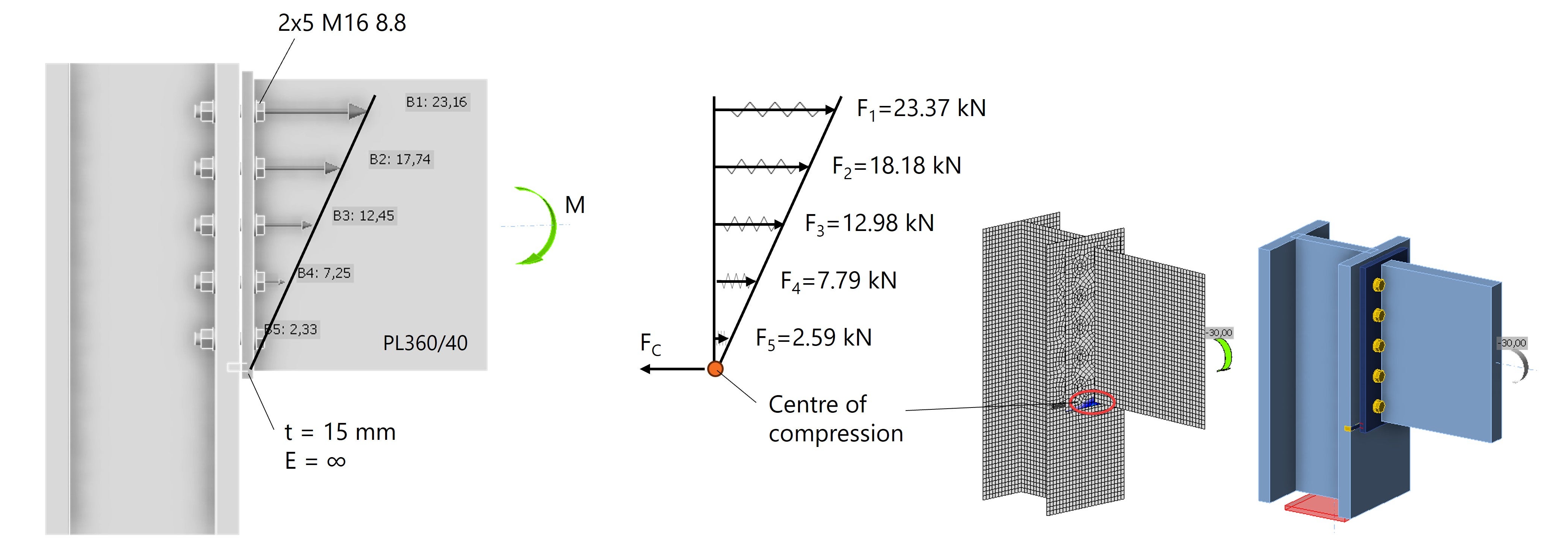
Le forze calcolate F₁ -F₅ corrispondono fedelmente alle forze del bullone in IDEA StatiCa, vedi Fig. 4.

Fig. 4: Distribuzione lineare della forza del bullone in IDEA StatiCa con il punto di compressione alla base della piastra terminale.

Il calcolo manuale è ben comparabile con il calcolo CBFEM in IDEA StatiCa, ma questo è possibile solo perché si assume una piastra terminale non realisticamente rigido e un centro di rotazione forzato. Modelliamo ora la piastra di estremità con il modulo di elasticità reale E=210 GPa.

3 - Piastra di estremità flessibile

Riprendiamo lo stesso esempio della situazione 2, ma ora la piastra di estremità è in acciaio S235 con E=210 GPa. La distribuzione rimane lineare, ma le forze del bullone aumentano di valore e non sono più direttamente paragonabili al nostro calcolo manuale. Cosa sta succedendo?

Analizzando attentamente i risultati in IDEA StatiCa, vediamo che si verificano deformazioni nella piastra di estremità e nasce l'effetto leva. La forza di trazione provoca la deformazione della piastra di estremità, creando ulteriori sollecitazioni di compressione sui lati che incrementano le forze del bullone. Questo effetto leva è ben visibile in IDEA StatiCa attraverso la visualizzazione delle tensioni di contatto tra la piastra di estremità e l'ala della colonna, vedi Fig. 5.

Fig. 5: Le forze dei bulloni aumentano a causa dell'effetto leva (forze di trazione).

In IDEA StatiCa, le prying force sono automaticamente incluse nel calcolo FEM e tutti i bulloni sono verificati di conseguenza. Il ricalcolo manuale è possibile ma richiede più tempo.

Finora abbiamo modellato la trave come una piastra PL360/40, per analizzare una distribuzione delle forze il più possibile prevedibile. Ma cosa succede se la trave è un IPE360?

4 - E se la trave fosse un profilo a I?

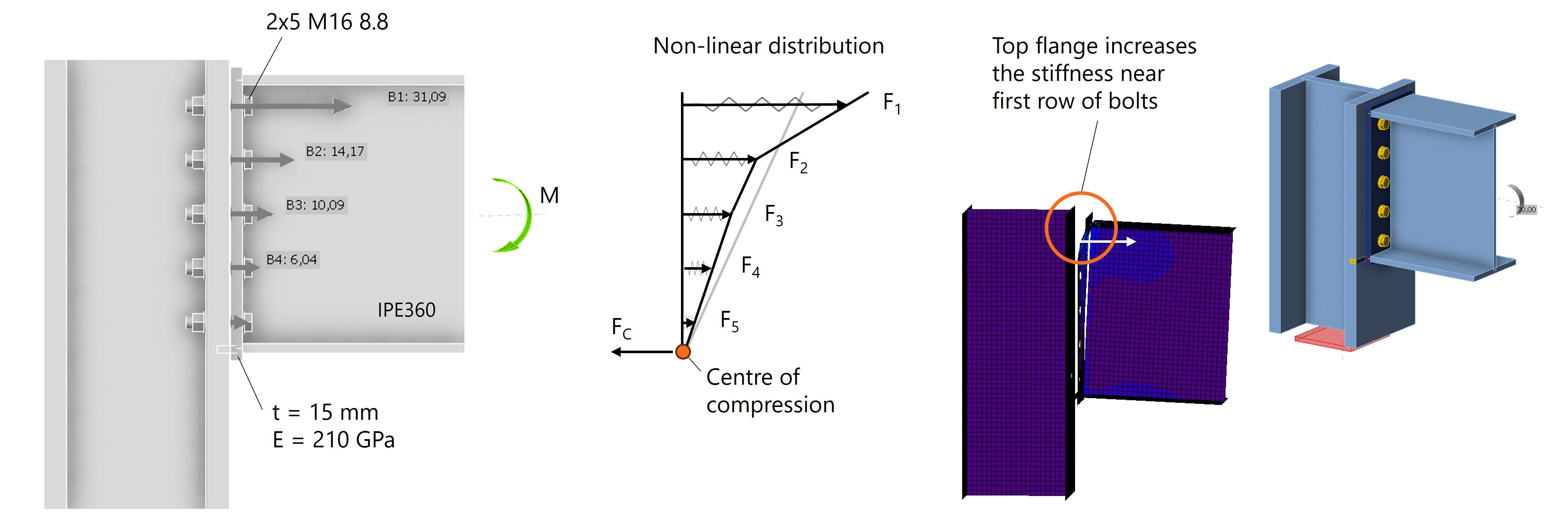
Se modelliamo la trave come un profilo a I, che è più comune nella pratica, la rigidezza relativa nella connessione cambia. La presenza di un'ala superiore aumenta la rigidezza intorno alla fila di bulloni superiore. E cosa succede quando la rigidezza aumenta? Le parti più rigide assorbono più forza, aumentando le forze dei bulloni nella fila superiore.

Il risultato è una distribuzione non lineare delle forze dei bulloni, come mostrato in Fig. 6.

Fig. 6: Distribuzione non lineare delle forze sui bulloni dovuta alla variazione dei rapporti di rigidezza.

Quando si distribuiscono le forze su un giunto, è necessario considerare i rapporti di rigidezza all'interno del giunto. Questa è la parte più difficile del processo di calcolo, perché molti fattori possono influenzarla. Si consideri, ad esempio:

• Spessore della piastra di estremità
• Tipo di sezione trasversale
• Irrigidimenti
• Schema dei bulloni
• Proprietà del materiale
• Comportamento elastico o plastico

Analizzando i risultati in IDEA StatiCa, si ottiene una visione della distribuzione delle forze e si può ottimizzare il progetto, se necessario.

5 - Posizionare i bulloni dove contribuiscono di più

Infine, viene mostrato come la distribuzione delle forze possa essere influenzata dallo spostamento dei bulloni, con l'obiettivo di creare il progetto più efficace possibile.

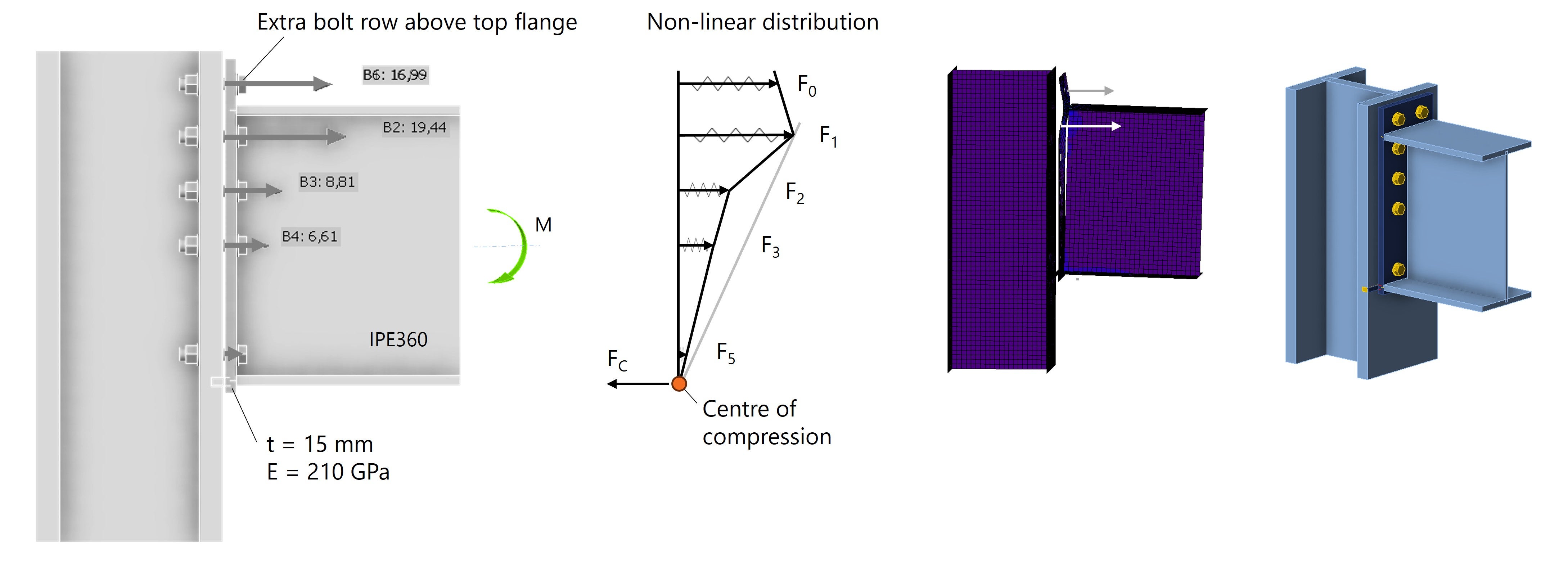
Se si ipotizza che sia presente solo un momento flettente verso il basso, la posizione più efficace per i bulloni è vicino all'ala superiore. Questa posizione è la più lontana dal centro di rotazione e si trova nella parte più rigida, vicino alle flange. Allungando la piastra di estremità e spostando la fila di bulloni 4 al di sopra dell'ala superiore, le forze vengono ridotte e distribuite meglio ai bulloni delle due file superiori, vedi Fig. 7.

Fig. 7: I bulloni vicino all'ala superiore assorbono la forza maggiore.

La sezione sopra l'ala superiore è meno rigida di quella sotto l'ala superiore, quindi i bulloni della fila 0 assorbono una forza leggermente inferiore. Si potrebbe ottimizzare ulteriormente questo aspetto aggiungendo un irrigidimento nella parte superiore, vedi Fig. 8.

Conclusione

La distribuzione della forza dei bulloni in una piastra di estremità non è mai perfettamente lineare nella pratica. Le variazioni della rigidezza, della deformazione e degli effetti leva determinano un andamento complesso delle forze, per cui i calcoli manuali possono fornire solo un'indicazione approssimativa.

Con IDEA StatiCa, possiamo analizzare il comportamento effettivo della connessione. Il software mostra come vengono distribuite le forze e come fattori quali lo spessore della piastra, il tipo di sezione, la rigidezza del materiale e il posizionamento dei bulloni influenzino i risultati. Questa visione consente agli ingegneri di andare oltre le verifiche di base del codice e di ottimizzare realmente i loro progetti, ad esempio riposizionando i bulloni o aggiungendo irrigidimenti dove necessario.

Osservazione conclusiva

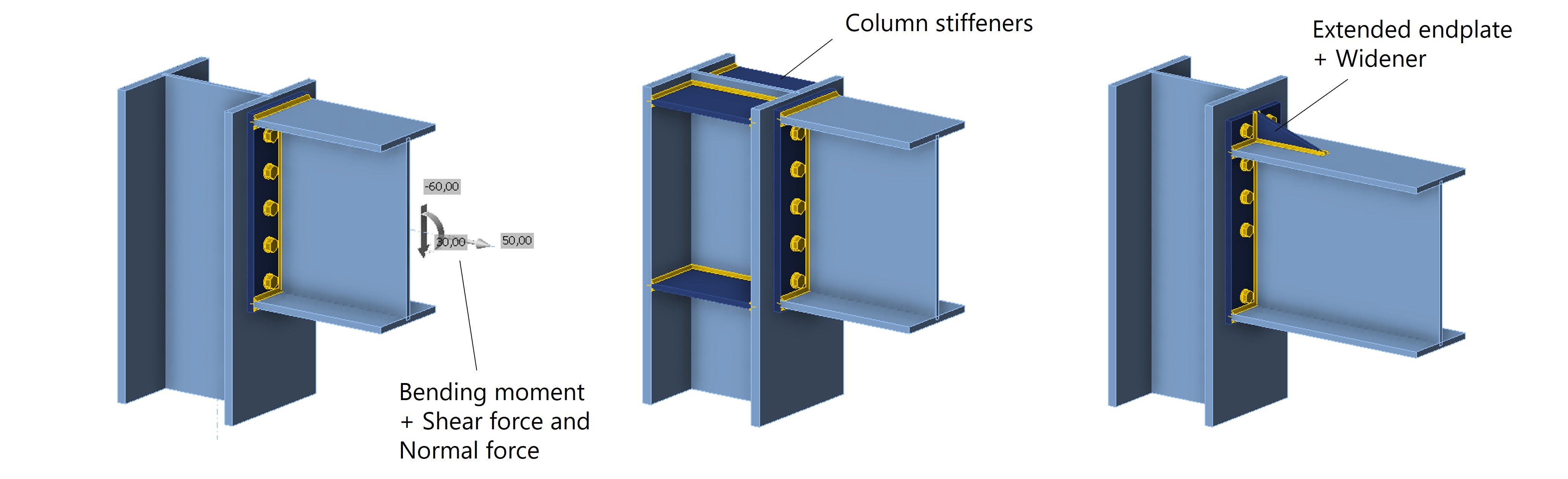
Questo studio è stato limitato a una connessione trave-colonna con piastra di estremità sottoposta a momento flettente. Si può immaginare che la distribuzione della forza dei bulloni diventi ancora più complessa se si applica anche una forza di taglio o normale, se si utilizzano sezioni trasversali di altri profili, se si aggiungono irrigidimenti e così via. Tutti questi fattori influenzano la distribuzione della forza modificando la rigidezza dei vari componenti.

Fig. 8: Collegamento della piastra di estremità con altre forze interne - irrigidimenti della colonna - piastra di estremità estesa con irrigidimento.