Schraubenkraftverteilung bei einem Träger/Stütze-Stirnplattenanschluss

In diesem Beitrag wird die Verteilung der Schraubenkräfte und die maßgebenden Einflussfaktoren erläutert. Die tatsächliche Kraftverteilung in einem Anschluss lässt sich meist nicht direkt bestimmen. Dazu ist ein Verständnis des Tragverhaltens und der unterschiedlichen Steifigkeiten und Verformungen erforderlich. IDEA StatiCa Connection ermöglicht es, diese Effekte sichtbar zu machen. Die Ergebnisse aus IDEA StatiCa werden mit einer Handrechnung unter Annahme einer linearen Kraftverteilung verglichen und zeigen, warum die reale Schraubenkraftverteilung fast immer nichtlinear ist.

Beispiel und Randbedingungen

Zur Veranschaulichung wird eine Stirnplattenverbindung zwischen Träger und Stütze mit 2 × 5 M16 8.8-Schrauben und einem reinen Biegemoment am Träger betrachtet. Die Schweißnähte werden als Stumpfnähte modelliert und hier nicht weiter betrachtet. In fünf Schritten wird gezeigt, wie verschiedene Faktoren die Schraubenkraftverteilung beeinflussen.

1 - Freier Rotationspunkt

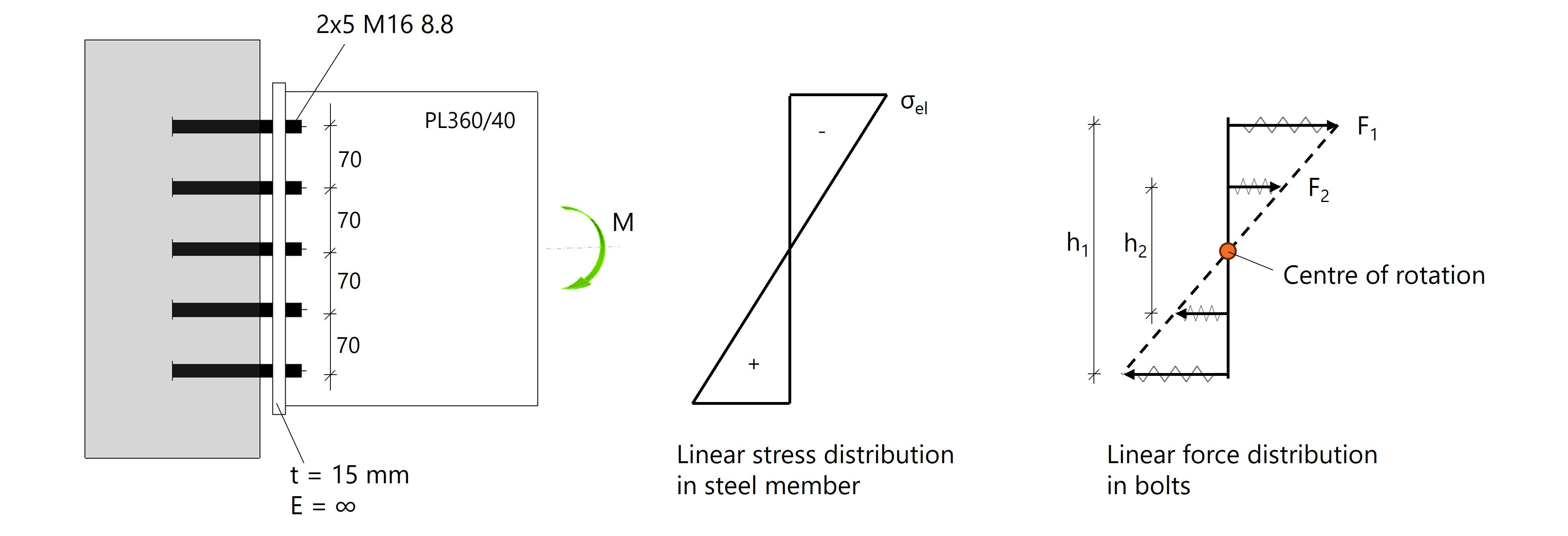
Zunächst wird ein theoretischer Fall betrachtet, bei dem der Träger als Platte PL 360/40 modelliert wird. Das aufgebrachte Biegemoment erzeugt eine linear-elastische Spannungsverteilung mit der neutralen Faser in der Mitte. Diese Spannungen lassen sich in eine entsprechende lineare Schraubenkraftverteilung übersetzen – allerdings nur, wenn die Steifigkeiten symmetrisch sind, die Schrauben auch Druckkräfte übertragen und das System vollständig elastisch bleibt.

Zur Annäherung dieses Idealfalls wird der Anschluss mit einer unendlich steifen Stirnplatte (E = ∞) und einem Spalt modelliert. Das System verhält sich in Zug und Druck identisch, sodass sich ein idealer Rotationspunkt in der mittleren Schraubenreihe ergibt.

Abb. 1: Spannungsverteilung im Träger entspricht der Schraubenkraftverteilung infolge freier Rotation.

Die lineare Kraftverteilung kann per Handrechnung überprüft werden. Wenn Fᵢ die Kraft in einer einzelnen Schraube darstellt, ergibt sich folgendes Gleichgewicht:

\( M = 2F_1 \cdot h_1 + 2F_2 \cdot h_2 \).

Da die Schraubenabstände gleich sind, ergibt sich:

\( F_2 = \frac{1}{2} \cdot F_1 \).

In allen Beispielen beträgt das Biegemoment M = 30 kNm.

Setzt man dies ein, lassen sich die Schraubenkräfte F₁ und F₂ wie folgt bestimmen:

\( M = 2F_1 \cdot h_1 + F_1 \cdot h_2 = 2F_1 \cdot 0.28 + F_1 \cdot 0.14 = 0.70 F_1 = 30 \) kNm

\( F_1 = 30 / 0.70 = 42.86 \) kN (pro Schraube)

\( F_2 = F_1 / 2 = 42.86 / 2 = 21.43 \) kN (pro Schraube)

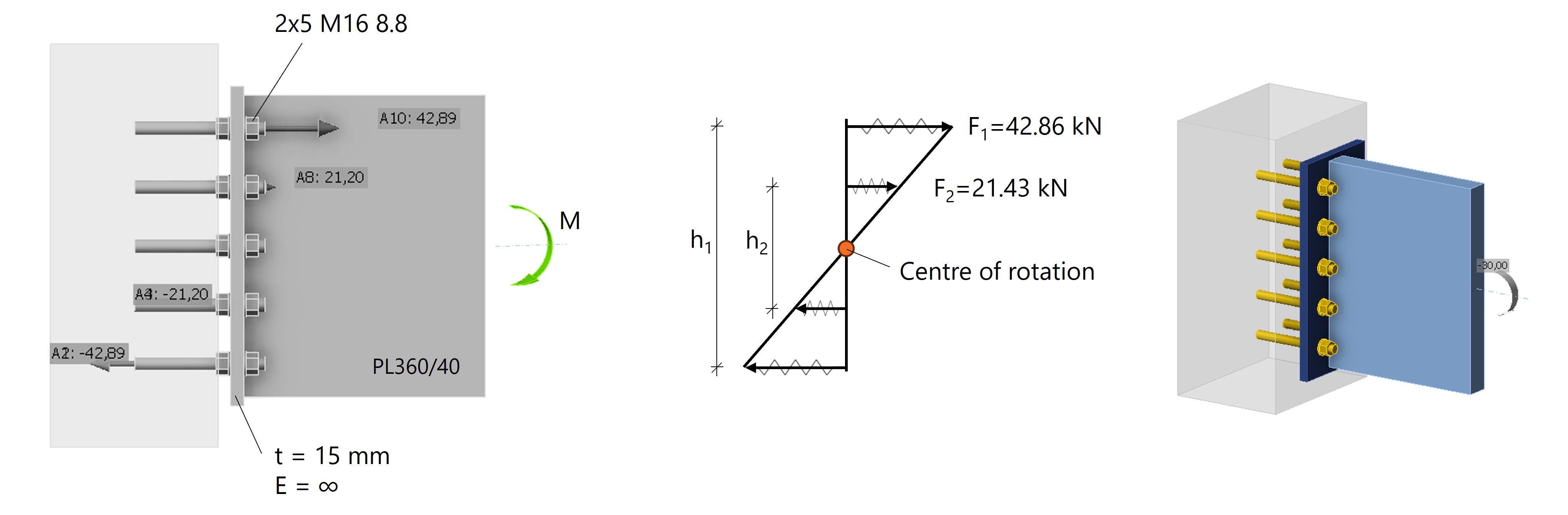
Die Ergebnisse für F₁ and F₂ werden den in IDEA StatiCa berechneten Schraubenkräften gegenübergestellt. Wie unten zu sehen, sind die Schraubenkräfte nahezu identisch.

Abb. 2: Lineare Schraubenkraftverteilung in IDEA StatiCa durch Modellierung der Schrauben als Anker.

(Hinweis: Für diesen Vergleich muss eine unendlich steife Stirnplatte angenommen und der Träger als Platte PL 360/40 statt als I-Profil modelliert werden.)

2 - Erzwungener Rotationspunkt

In der Realität übertragen Schrauben keine Druckkräfte; der Druck wird über den Kontakt zwischen Stirnplatte und Stützenflansch eingeleitet. Die Steifigkeiten ändern sich dadurch, und der Rotationspunkt – jetzt „Druckpunkt“ genannt – verschiebt sich nach unten.

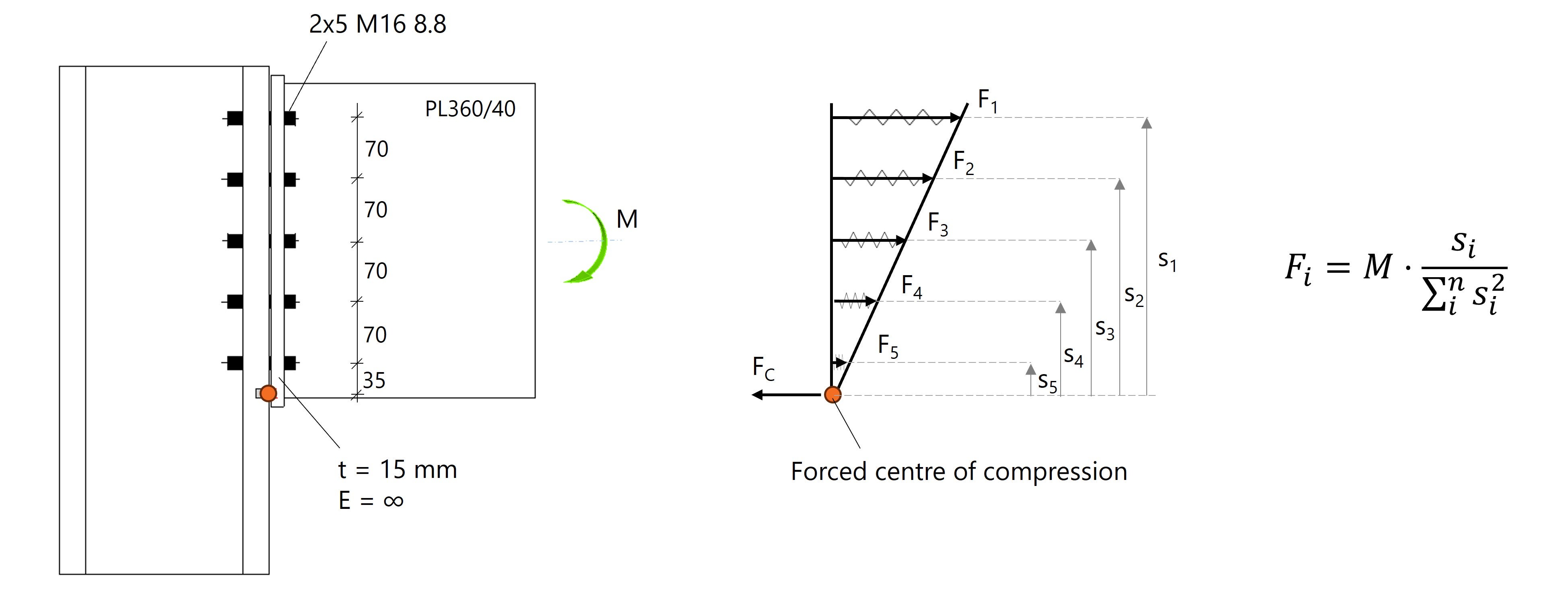
Zur vergleichbaren Handrechnung wird eine schmale Kontaktzone am unteren Ende der Stirnplatte modelliert, sodass das Druckzentrum immer am Plattenrand liegt. Die Stahlteile erhalten einen hohen E-Modul, um Verformungen zu minimieren. Dadurch entsteht eine perfekt lineare Schraubenkraftverteilung mit Rotationspunkt am Plattenende.

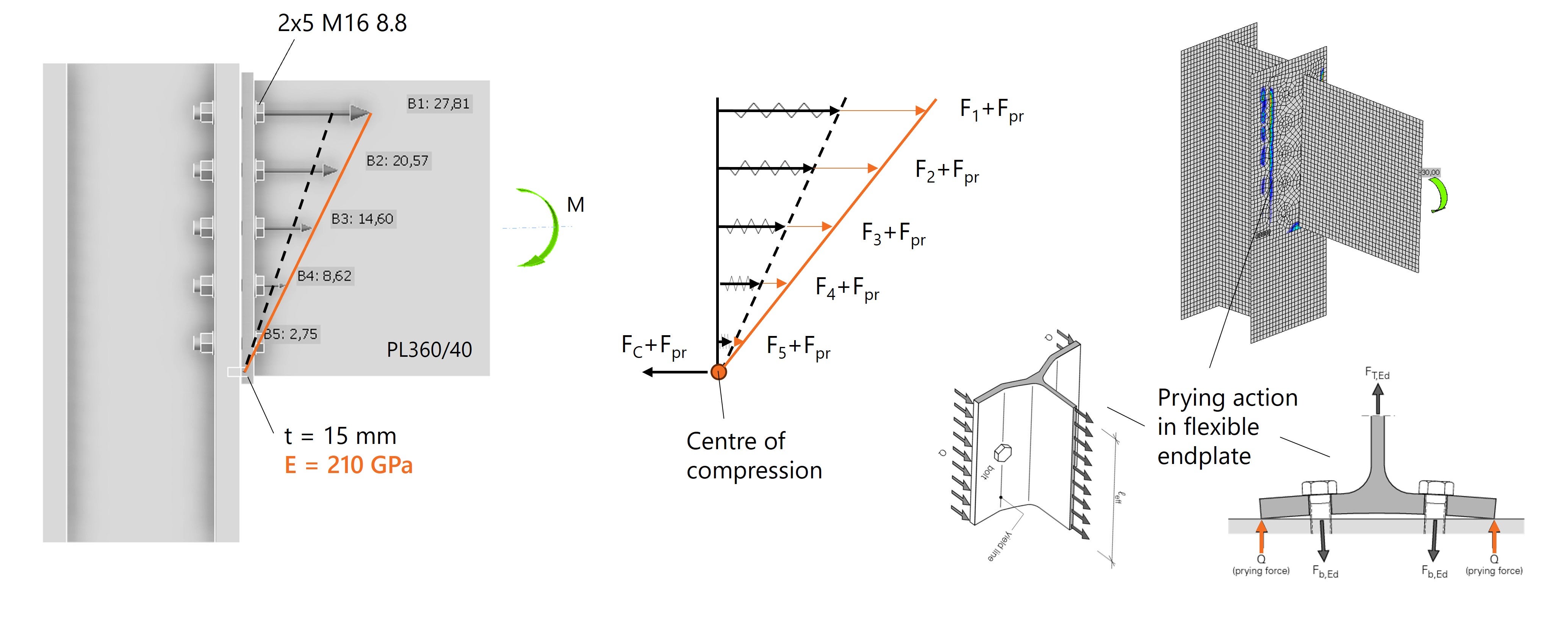
Abb. 3: Lineare Schraubenkraftverteilung mit Rotationszentrum (Druckpunkt) am unteren Rand der Stirnplatte.

Auf Grundlage der bekannten Abstände und Lasten werden die Schraubenkräfte nach folgender Gleichung berechnet:

           \( F_i = M \cdot \frac{s_i}{\sum_{i}^{n} s_i^{2}} \).

Jede Schraubenreihe besteht aus zwei Schrauben, und es wird angenommen, dass die Kräfte gleich groß sind.
Für die erste Schraubenreihe ergibt sich:

\( 2F_1 = M \cdot \frac{s_1}{\sum_{i}^{n} s_i^{2}} = 30 \cdot \frac{0.315}{(0.315^2+0.245^2+0.175^2+0.105^2+0.035^2)} \} = 46.75 \) kN

Das ergibt \( F_1 = 46.75/2 = 23.37 \) kN

Auf diese Weise lässt sich die Kraft einer einzelnen Schraube je Reihe berechnen:

• \( F_1 = 23.37 \) kN
• \( F_2 = 18.18 \) kN
• \( F_3 = 12.98 \) kN
• \( F_4 = 7.79 \) kN
• \( F_5 = 2.59 \) kN

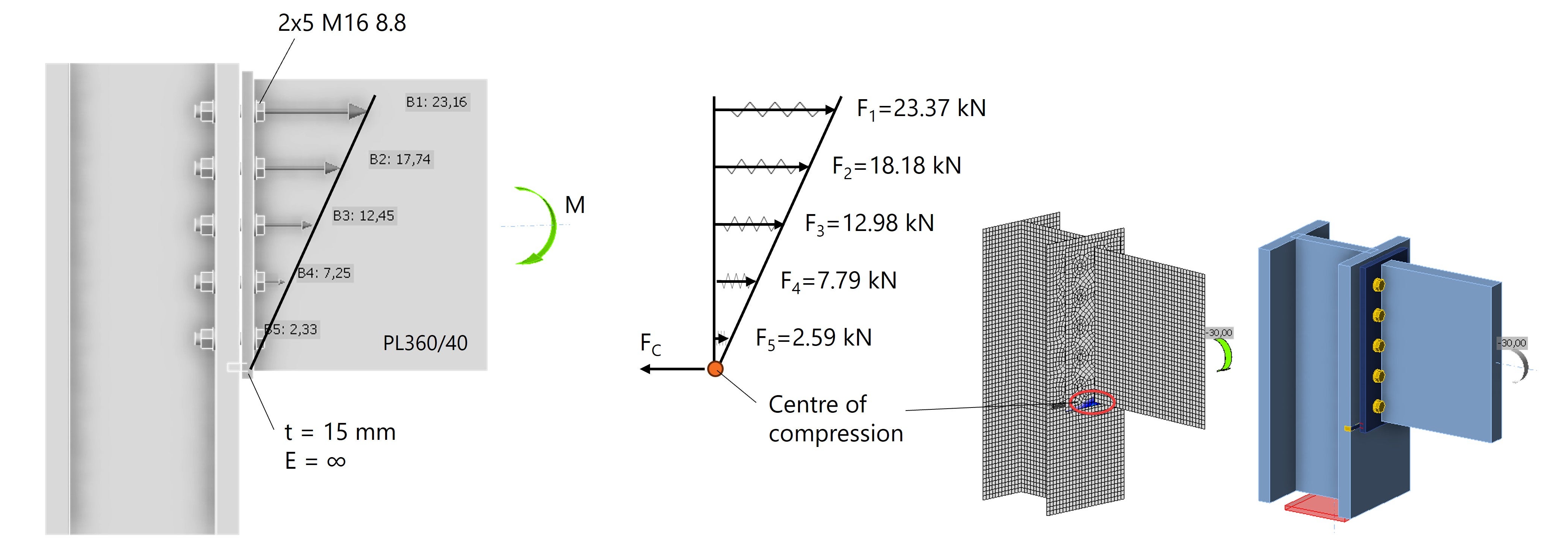
Die berechneten Kräfte F₁ - F₅ stimmen sehr gut mit den in IDEA StatiCa ermittelten Schraubenkräften überein, siehe Abb. 4.

Abb. 4: Lineare Schraubenkraftverteilung in IDEA StatiCa mit Druckpunkt am unteren Rand der Stirnplatte.

Die Handrechnung stimmt gut mit der CBFEM-Berechnung in IDEA StatiCa überein. Dies ist jedoch nur möglich, weil eine unrealistisch steife Stirnplatte und ein erzwungenes Rotationszentrum angenommen wurden. Im nächsten Schritt wird die Stirnplatte mit dem tatsächlichen Elastizitätsmodul modelliert.

3 - Verformbare Stirnplatte

Das Beispiel aus Punkt 2 wird beibehalten, jedoch mit Stahl S235 gerechnet. Die Verteilung bleibt zwar näherungsweise linear, die Schraubenkräfte steigen jedoch an und weichen von der Handrechnung ab.

Die Analyse zeigt, dass sich die Stirnplatte durch die Zugkräfte verformt und dadurch Hebelkräfte (Abstützkräfte) entstehen. Diese führen zu zusätzlichen Druckspannungen an den Plattenrändern und erhöhen die Schraubenkräfte. IDEA StatiCa zeigt diese Effekte anschaulich über die Kontaktspannungen zwischen Stirnplatte und Stützenflansch.

Abb. 5: Erhöhung der Schraubenkräfte infolge des Hebeleffekts (Abstützkräfte).

In IDEA StatiCa werden die Abstütz-Effekte automatisch in der FEM-Berechnung berücksichtigt; alle Schrauben werden entsprechend nachgewiesen. Eine manuelle Nachrechnung ist möglich, jedoch aufwändig.

4 - Was passiert bei einem I-Profil?

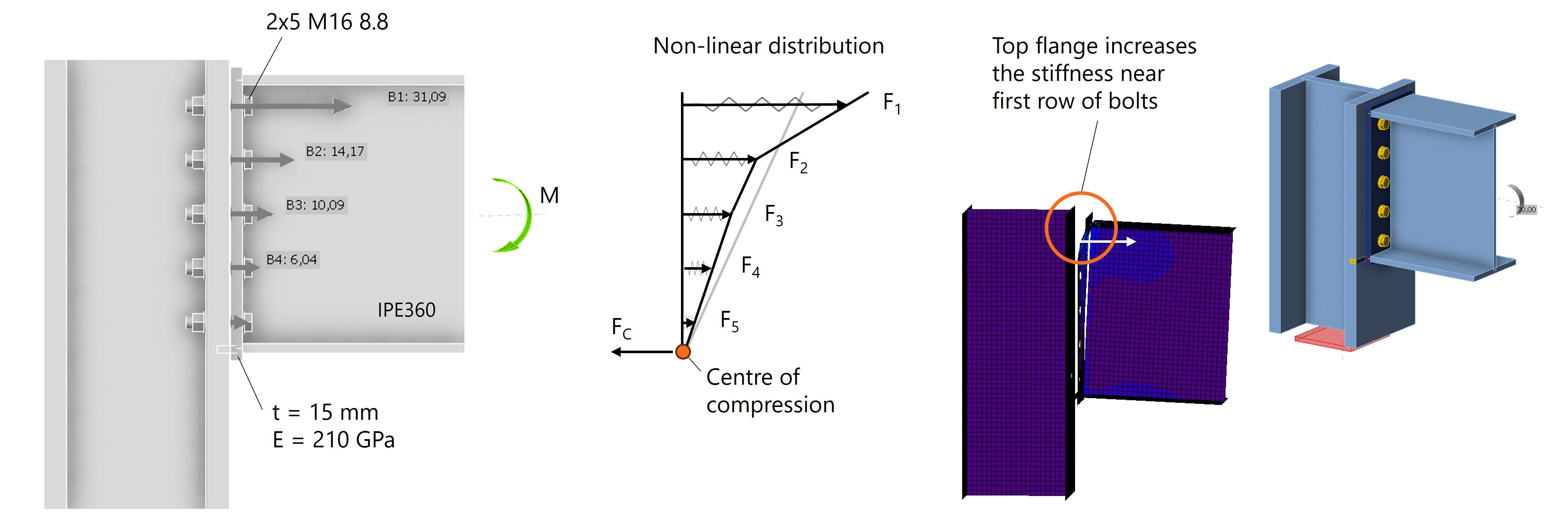
Wird der Träger als IPE 360 modelliert, verändert sich die relative Steifigkeit im Anschluss. Der Oberflansch erhöht die Steifigkeit im Bereich der oberen Schraubenreihe. Steifere Bereiche nehmen mehr Kraft auf – dadurch steigen die Schraubenkräfte oben deutlich an. Das Ergebnis ist eine nichtlineare Schraubenkraftverteilung.

Abb. 6: Nichtlineare Schraubenkraftverteilung infolge veränderter Steifigkeitsverhältnisse.

Bei der Ermittlung der Kräfte müssen daher die Steifigkeitsverhältnisse innerhalb des Anschlusses berücksichtigt werden. Sie hängen von vielen Faktoren ab, u. a.:

• Dicke der Stirnplatte
• Querschnittsform (I-, H-, oder Hohlprofil)
• Steifbleche oder Rippen
• Schraubenanordnung
• Werkstoffsteifigkeiten
• Elastisches oder plastisches Tragverhalten

IDEA StatiCa erlaubt es, diese Zusammenhänge sichtbar zu machen und das Anschlussdesign gezielt zu optimieren.

5 - Schrauben dort platzieren, wo sie am meisten beitragen

Zum Schluss wird gezeigt, wie sich die Kraftverteilung durch geschickte Anordnung der Schrauben beeinflussen lässt.

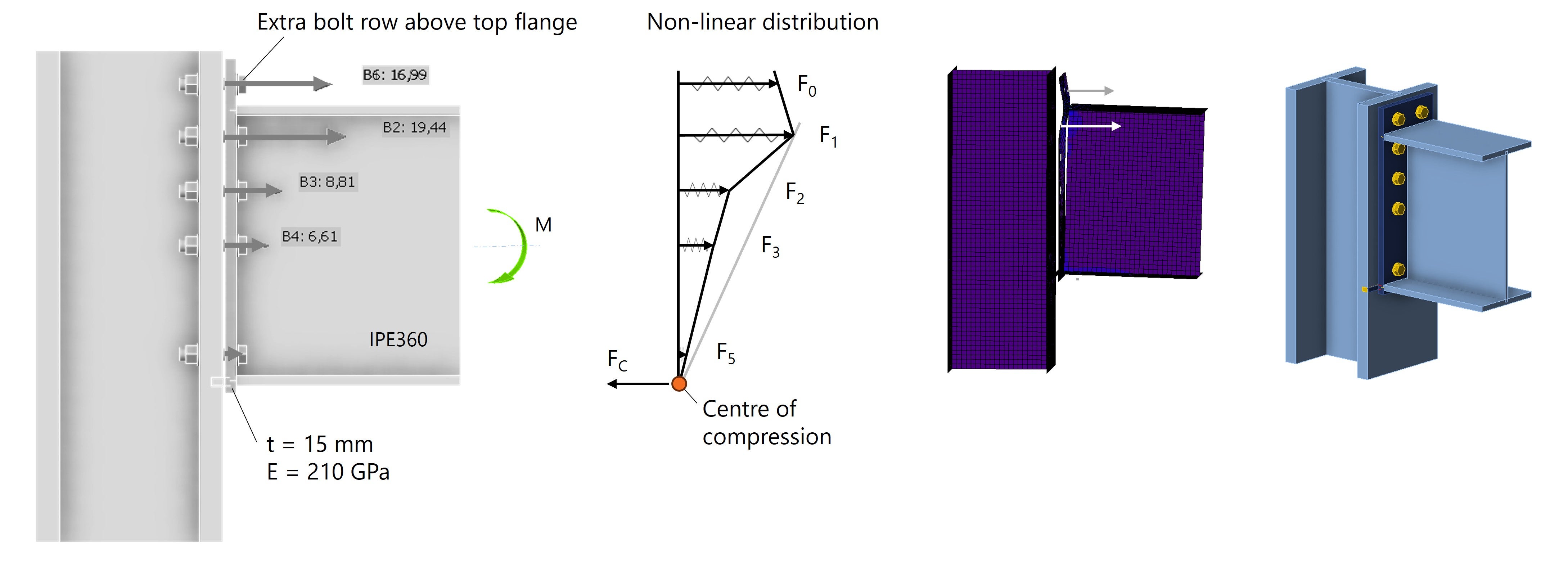
Liegt nur ein positives Biegemoment vor, ist die wirksamste Schraubenlage nahe der oberen Gurtplatte – dort ist der Abstand zum Rotationspunkt am größten und die Steifigkeit am höchsten. Wird die Stirnplatte nach oben verlängert und eine zusätzliche Schraubenreihe oberhalb des Obergurts angeordnet, verteilen sich die Kräfte gleichmäßiger auf die oberen Schraubenreihen. Eine weitere Verbesserung lässt sich durch das Anbringen eines Steifblechs über dem Obergurt erreichen.

Abb. 7: Die Schrauben in der Nähe des Obergurts nehmen die größten Kräfte auf.

Fazit

In der Praxis ist die Schraubenkraftverteilung in Stirnplattenanschlüssen nie perfekt linear. Unterschiede in Steifigkeit, Verformungen und Abstütz-Effekte führen zu komplexen Kraftverläufen. Handrechnungen können diese nur grob abschätzen.

Mit IDEA StatiCa Connection lässt sich das reale Tragverhalten des Anschlusses analysieren. Die Software zeigt anschaulich, wie sich Faktoren wie Plattendicke, Querschnittsform, Werkstoffsteifigkeit und Schraubenanordnung auf die Kraftverteilung auswirken. So können Tragwerksplaner über einfache Normnachweise hinaus ihre Anschlüsse gezielt optimieren - etwa durch geänderte Schraubenlagen oder zusätzliche Steifbleche.

Abschließende Bemerkung

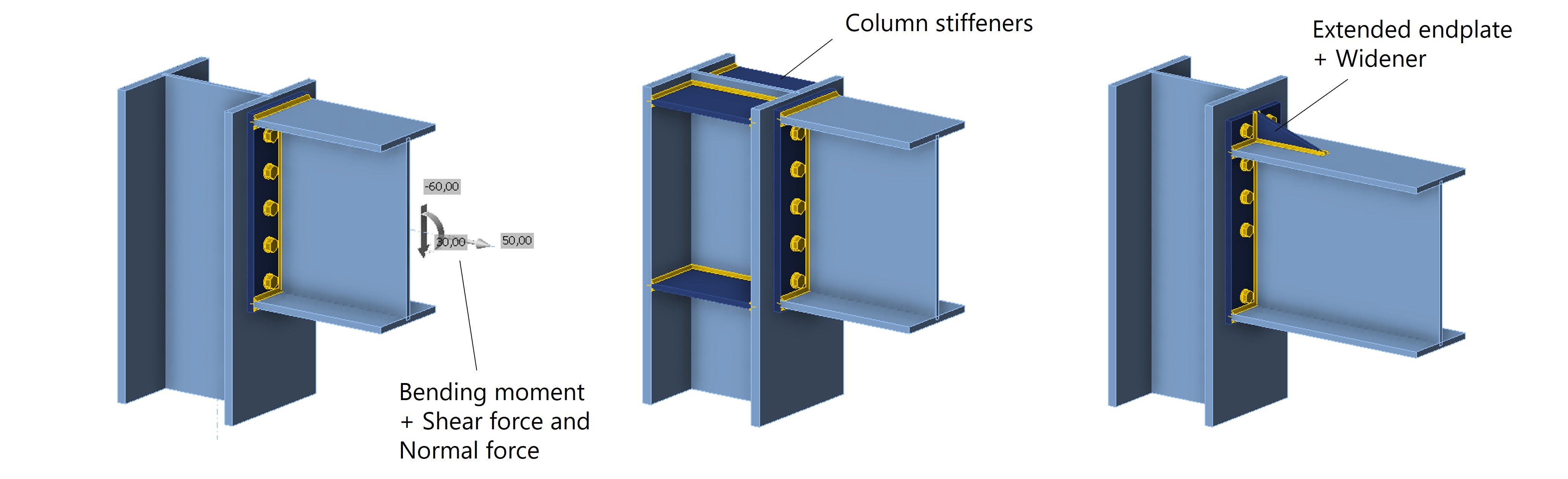
Diese Untersuchung beschränkt sich auf einen Stirnplattenanschluss zwischen Träger und Stütze unter reinem Biegemoment. Es liegt nahe, dass die Schraubenkraftverteilung noch deutlich komplexer wird, wenn zusätzlich Querkräfte oder Normalkräfte auftreten, andere Profilquerschnitte verwendet oder Steifbleche hinzugefügt werden. All diese Faktoren beeinflussen die Kraftverteilung, da sie die Steifigkeit der einzelnen Anschlusskomponenten verändern.

Abb. 8: Stirnplattenanschluss mit zusätzlichen Schnittgrößen - Stützensteifen und verlängerter Stirnplatte mit Steifenblech.