Bolt force distribution in end-plate beam-to-column connection

In this article, we discuss the distribution of bolt forces and the factors that affect it. Determining the actual force distribution in a joint is often impossible. This requires an understanding of joint behavior and knowledge of the different stiffnesses and deformations. IDEA StatiCa Connection helps provide insight into these effects. We compare the results from IDEA StatiCa with a hand calculation for a linear distribution and show why the actual force distribution is almost always nonlinear.

Format

We could discuss endless situations, but we will limit ourselves in this example to a beam-to-column end plate connection with 2x5 M16 8.8 bolts and a pure bending moment on the beam. The welds are modeled as butt welds and will not be discussed.

In the next 5 points, we discuss how various factors affect the bolt force distribution.

1 - Free centre of rotation

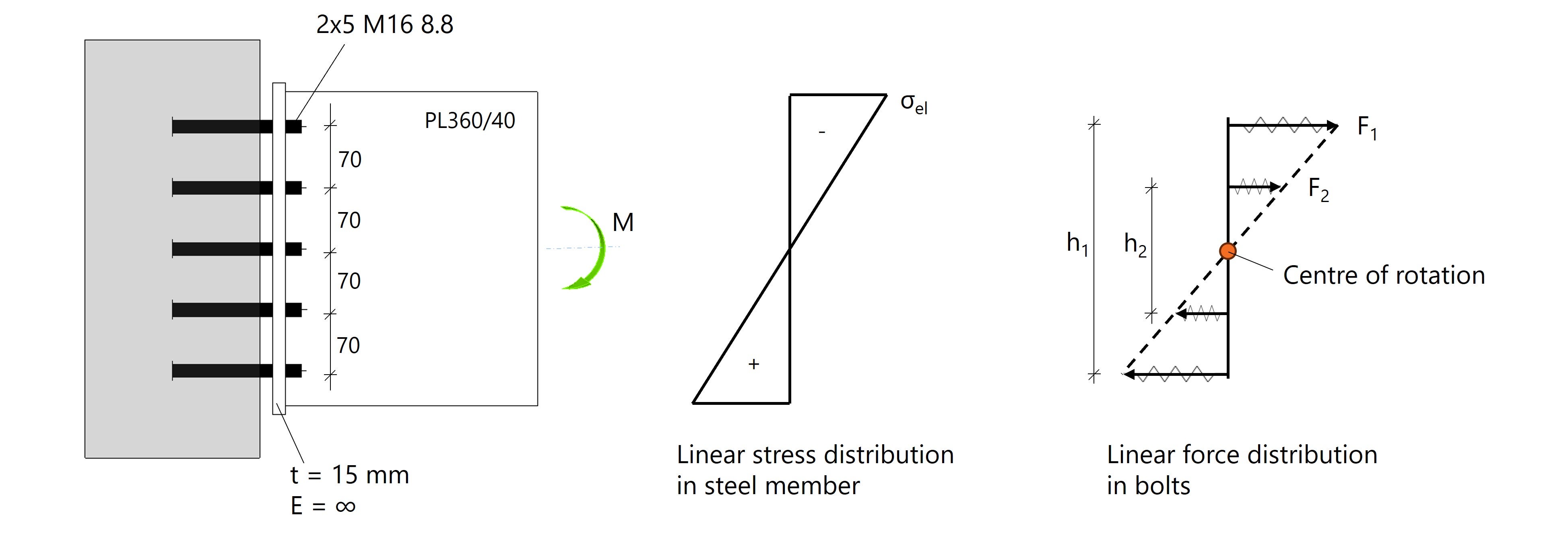
We begin with a theoretical example in which the beam is modeled as plate PL360/40. The bending moment acting on the beam creates a linear elastic stress distribution, with the neutral axis exactly in the middle. These stresses translate to a corresponding distribution of bolt forces, but only when the stiffnesses are symmetrical, the bolts can also transfer compressive forces, and the behavior remains fully elastic.

To approximate this, in situation 1 we modeled the joint as an infinitely stiff baseplate (E=∞) with anchors and a gap. The joint behaves the same in tension as in compression, creating an ideal rotation point located at the mid-bolt row.

Fig. 1: Stress distribution in beam is equal to force distribution in bolts due to free rotation.

We can check the linear force distribution with a hand calculation. If F_i represents the force in one bolt, we get the following equilibrium:

\( M = 2F_1 \cdot h_1 + 2F_2 \cdot h_2 \).

Since the bolt spacings are equal we get:

\( F_2 = \frac{1}{2} \cdot F_1 \).

The bending moment in all examples is M = 30 kNm.

If we fill this in, we can calculate F₁ and F₂:

\( M = 2F_1 \cdot h_1 + F_1 \cdot h_2 = 2F_1 \cdot 0.28 + F_1 \cdot 0.14 = 0.70 F_1 = 30 \) kNm

\( F_1 = 30 / 0.70 = 42.86 \) kN (per bolt)

\( F_2 = F_1 / 2 = 42.86 / 2 = 21.43 \) kN (per bolt)

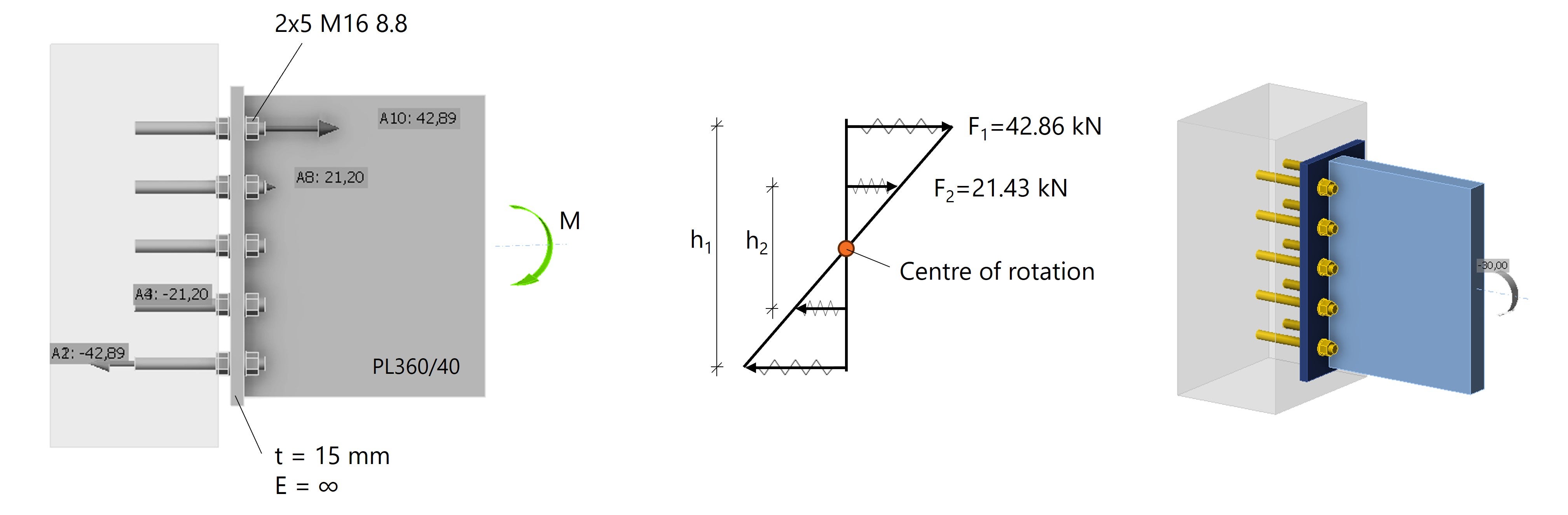
The results for F₁ and F₂ are compared to the calculated bolt forces in IDEA StatiCa. Below we see that the forces in the bolts are almost the same.

Fig. 2: Linear bolt force distribution in IDEA StatiCa by modeling the bolts as anchors.

*Note: To compare the CBFEM calculation with the hand calculation, we must assume an infinitely stiff endplate and model the beam as a plate PL360/40 instead of an I-profile. Later we will see why this is important.

2 - Forced centre of rotation

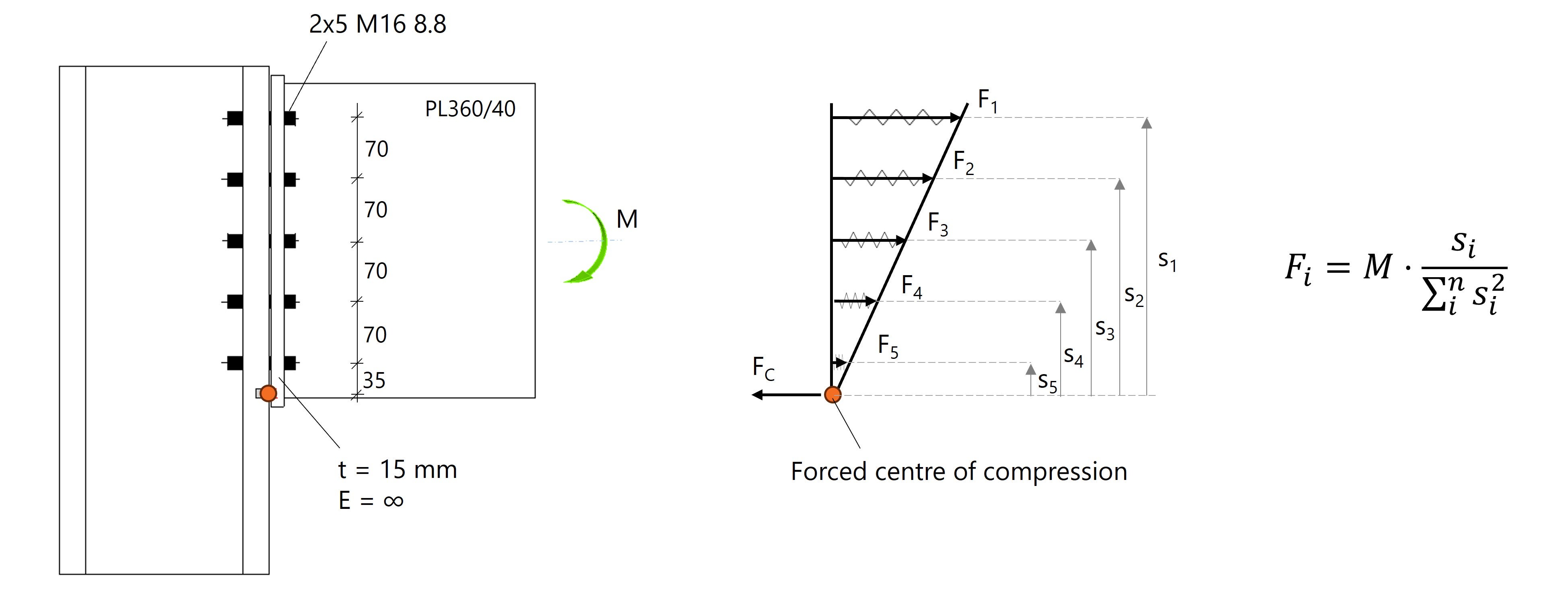
In a realistic end-plate connection, the bolts do not transfer compressive forces and compression is transmitted through contact between the endplate and the column flange. There is a change in stiffnesses that causes the centre of rotation, now called the centre of compression, to shift downward.

In order to compare hand calculations properly, we have modeled a narrow strip at the bottom of the endplate so that the centre of compression is always at the bottom of the endplate.

In addition, the beam was modeled as a plate and we increased the E-modulus of the steel parts to limit the deformations. This creates a perfectly linear distribution of bolt forces with the centre of rotation at the bottom of the endplate.

Fig. 3: Linear bolt force distribution with the centre of rotation (compression) at the bottom of the endplate.

Based on the known distances and loads, the bolt forces are calculated using the following equation:

           \( F_i = M \cdot \frac{s_i}{\sum_{i}^{n} s_i^{2}} \).

Each bolt row has 2 bolts and we assume that the forces are equal. For bolt row 1, we get:

\( 2F_1 = M \cdot \frac{s_1}{\sum_{i}^{n} s_i^{2}} = 30 \cdot \frac{0.315}{(0.315^2+0.245^2+0.175^2+0.105^2+0.035^2)} \} = 46.75 \) kN

That gives \( F_1 = 46.75/2 = 23.37 \) kN

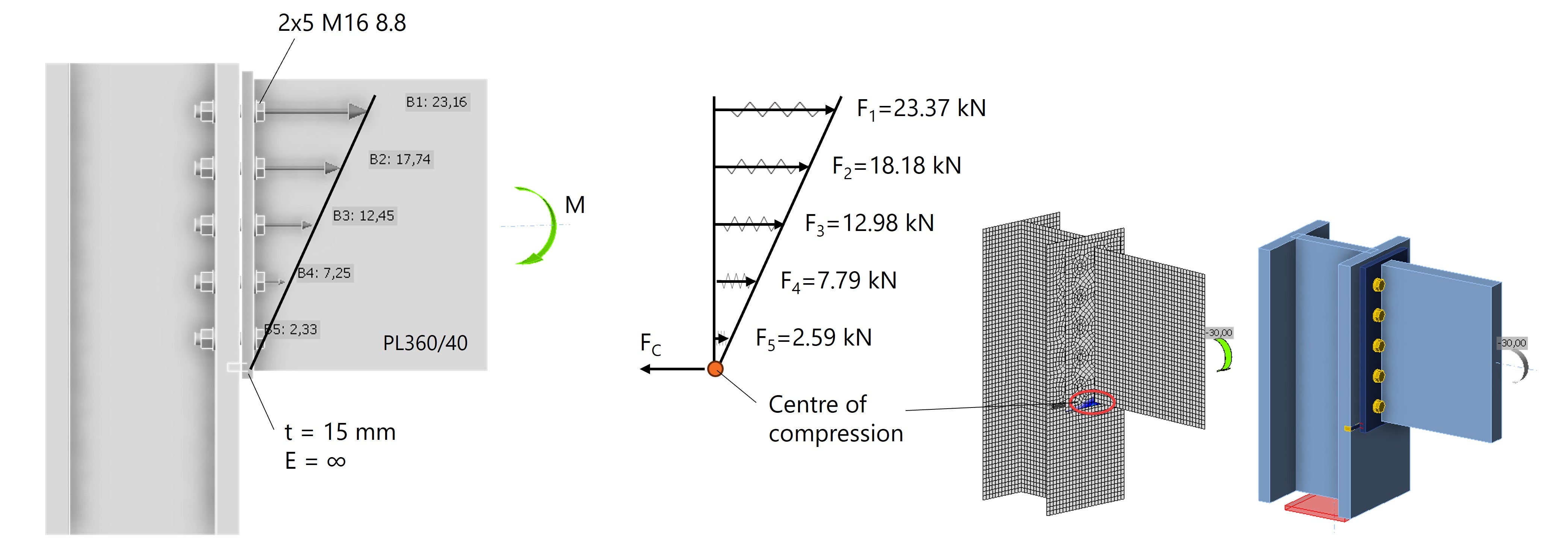
In this way, we can calculate the force of one bolt per row:

• \( F_1 = 23.37 \) kN
• \( F_2 = 18.18 \) kN
• \( F_3 = 12.98 \) kN.
• \( F_4 = 7.79 \) kN
• \( F_5 = 2.59 \) kN

The calculated forces F₁ - F₅ closely match the bolt forces in IDEA StatiCa, see Fig. 4.

Fig. 4: Linear bolt force distribution in IDEA StatiCa with the compression point at the bottom of the endplate.

The hand calculation compares well with the CBFEM calculation in IDEA StatiCa, but this is only possible because we assume an unrealistically stiff endplate and a forced centre of rotation. Let us now model the endplate with the actual modulus of elasticity E=210 GPa.

3 - Flexible endplate

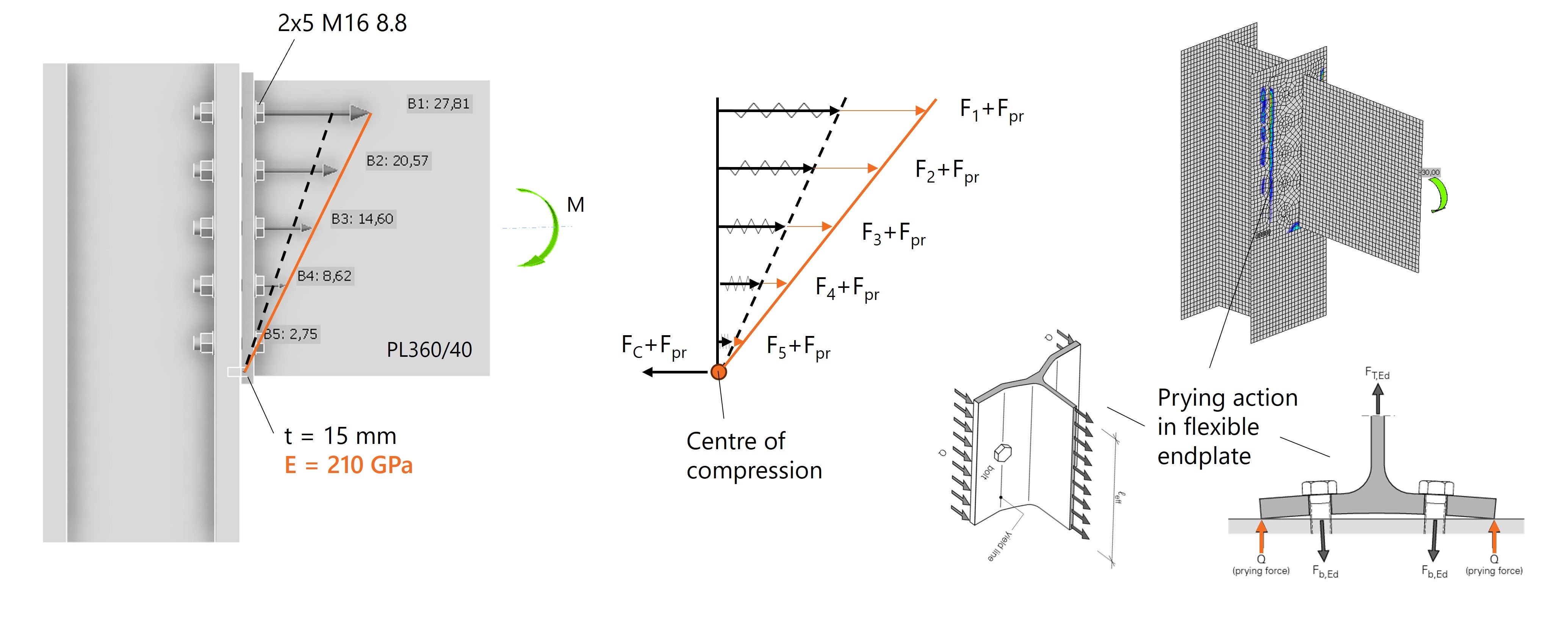
We take the same example as in situation 2, but now the endplate is made of steel S235 with E=210 GPa. The distribution remains linear, but the bolt forces increase in value, and are no longer directly comparable to our hand calculation. What is going on here?

By carefully analyzing the results in IDEA StatiCa, we see deformations in the endplate and prying action occurs. The tensile force causes deflection of the endplate, creating additional compressive stresses on the sides that increase the bolt forces. This leverage effect is well visible in IDEA StatiCa by displaying the contact stresses between the endplate and the column flange, see Fig. 5.

Fig. 5: Bolt forces increase as a result of the lever effect (prying forces).

In IDEA StatiCa, prying forces are automatically included in the FEM calculation and all bolts are checked accordingly. Recalculation by hand is possible but takes more time.

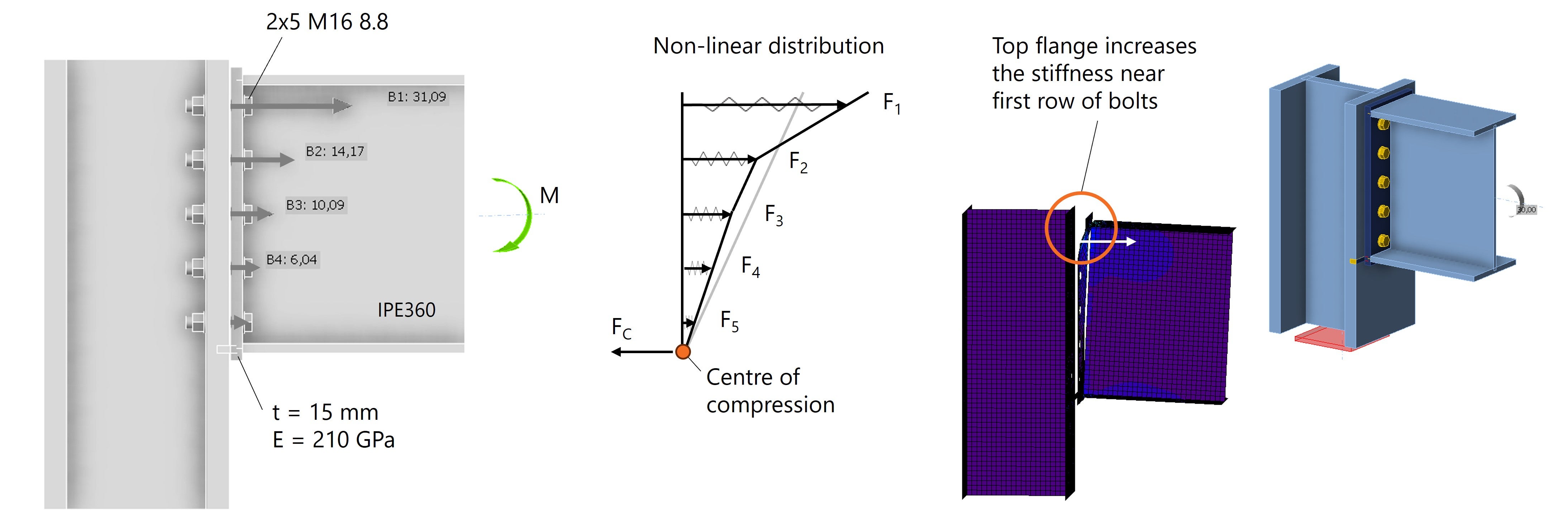
Until now, we have modeled the beam as plate PL360/40, in order to analyze a force distribution that is as predictable as possible. But what if the beam is an IPE360?

4 - What if the beam is an I-profile?

If we model the beam as an I-profile, which is more common in practice, the relative stiffness in the connection changes. The presence of a top flange increases the stiffness around the top bolt row. And what happens when the stiffness increases? The stiffer parts absorb more force, increasing the bolt forces in the top row.

The result is a non-linear distribution of bolt forces, as shown in Fig. 6.

Fig. 6: Non-linear bolt force distribution due to a change in stiffness ratios.

When distributing forces across a joint, the stiffness ratios within the joint must be considered. This is the most difficult part of the calculation process, because many factors can influence it. Consider, for example:

• Thickness of endplate
• Type of cross-section
• Stiffeners
• Bolt pattern
• Material properties
• Elastic or plastic behavior

By analyzing the results in IDEA StatiCa, we gain insight into the force distribution and can optimize our design if necessary.

5 - Place bolts where they contribute the most

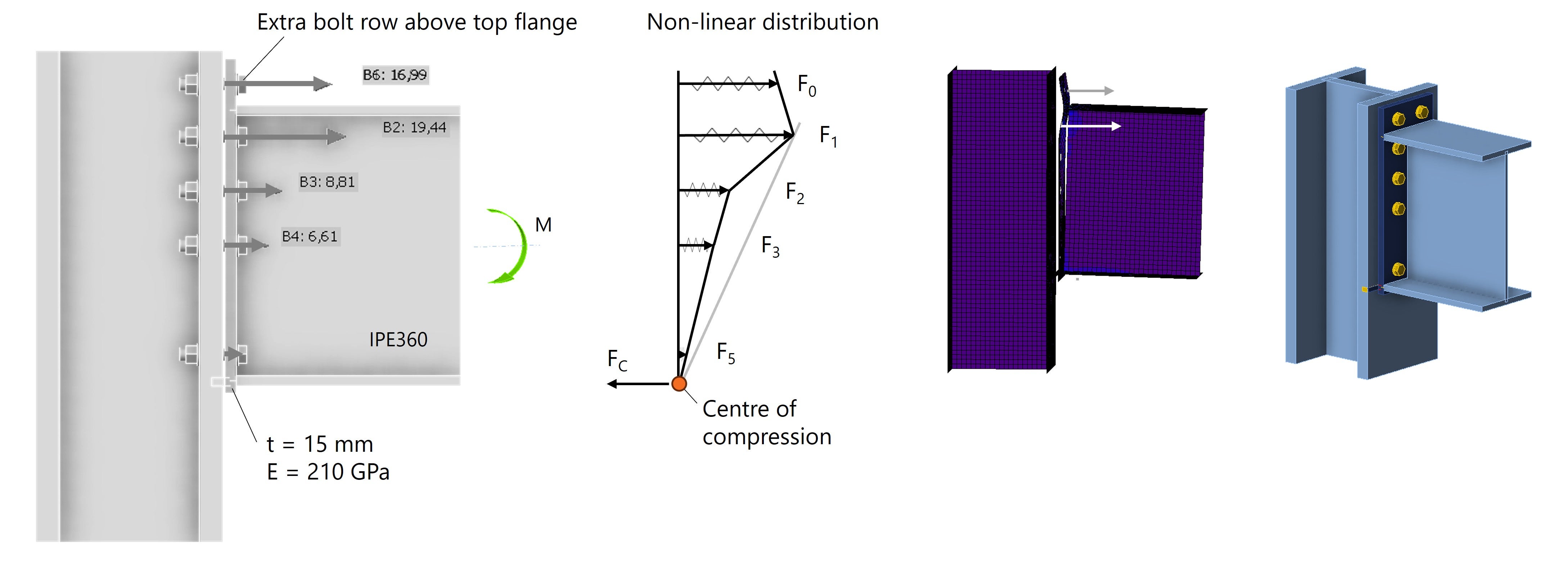
Finally, it is shown how the force distribution can be influenced by moving the bolts, with the goal of creating the most effective design possible.

If we assume that only a downward bending moment is present, then the most effective location for the bolts is near the top flange. This location is farthest from the centre of rotation and is in the stiffest part, close to the flanges. By extending the endplate and moving bolt row 4 above the top flange, the forces are reduced and better distributed to the bolts in the two top rows, see Fig. 7.

Fig. 7: The bolts near the top flange take the most force.

The section above the top flange is less stiff than below the top flange so the bolts in row 0 take a slightly smaller force. We could further optimize this by adding an stiffener at the top, see Fig. 8.

Conclusion

The bolt force distribution in an end plate is never perfectly linear in practice. Variations in stiffness, deformation, and prying effects lead to a complex force pattern, meaning that hand calculations can only provide a rough approximation.

With IDEA StatiCa, we can analyze the connection's actual behavior. The software shows how forces are distributed and how factors like plate thickness, section type, material stiffness, and bolt placement influence the results. This insight allows engineers to go beyond basic code checks and truly optimize their designs, for example, by repositioning bolts or adding stiffeners where needed.

Concluding remark

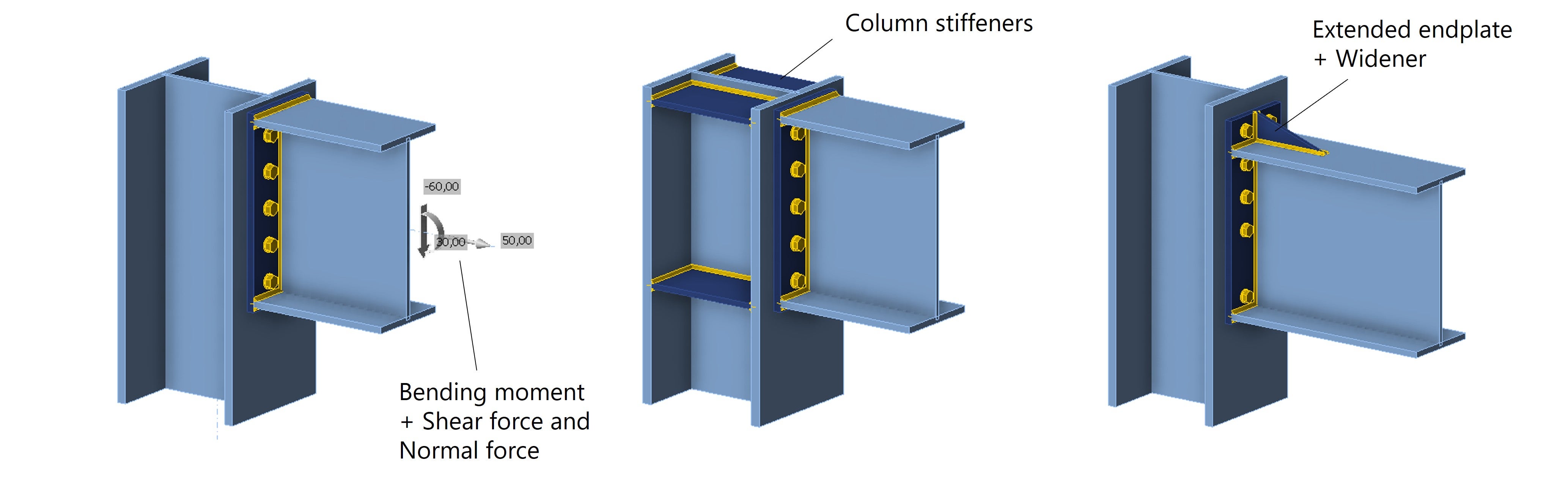
This study has been limited to a beam-to-column connection with endplate under bending moment. One can imagine that the bolt force distribution becomes even more complex when a shear or normal force is also applied, other profile cross-sections are used, stiffeners are added, and so on. All these factors affect the force distribution by changing the stiffness of the various components.

Fig. 8: End-plate connection with other internal forces - column stiffeners - extended endplate with stiffener.