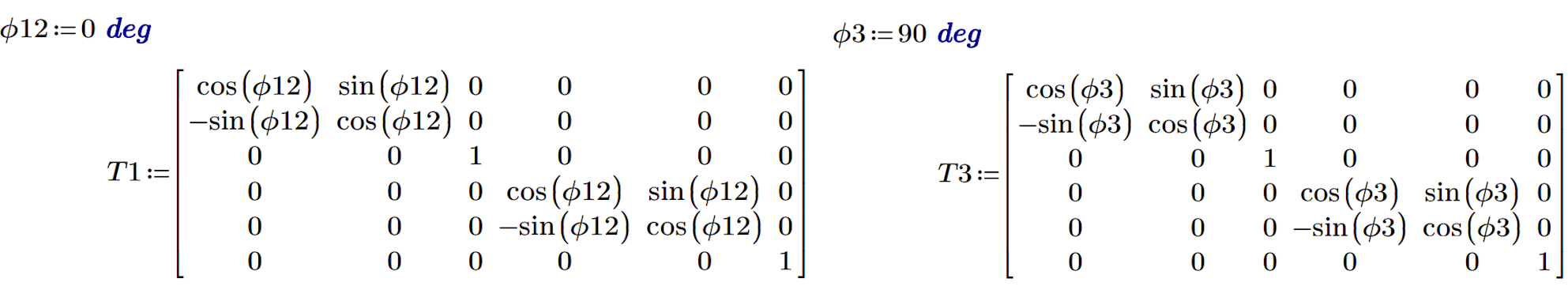Approccio diretto alla rigidezza

Motivazione

Conoscere a fondo l'analisi agli elementi finiti (FEA) è fondamentale sia per garantire input accurati sia per presentare i risultati nel modo giusto. L'obiettivo principale di questo articolo è spiegare come viene assemblata la matrice nel background di ogni software FEA e come la rigidità rotazionale può influenzare il comportamento globale di una struttura. Questo articolo serve come prerequisito per un prossimo articolo, in cui tutti i risultati saranno applicati a una struttura utilizzando IDEA StatiCa Connection.

L'approccio a rigidezza diretta - connessioni rigide

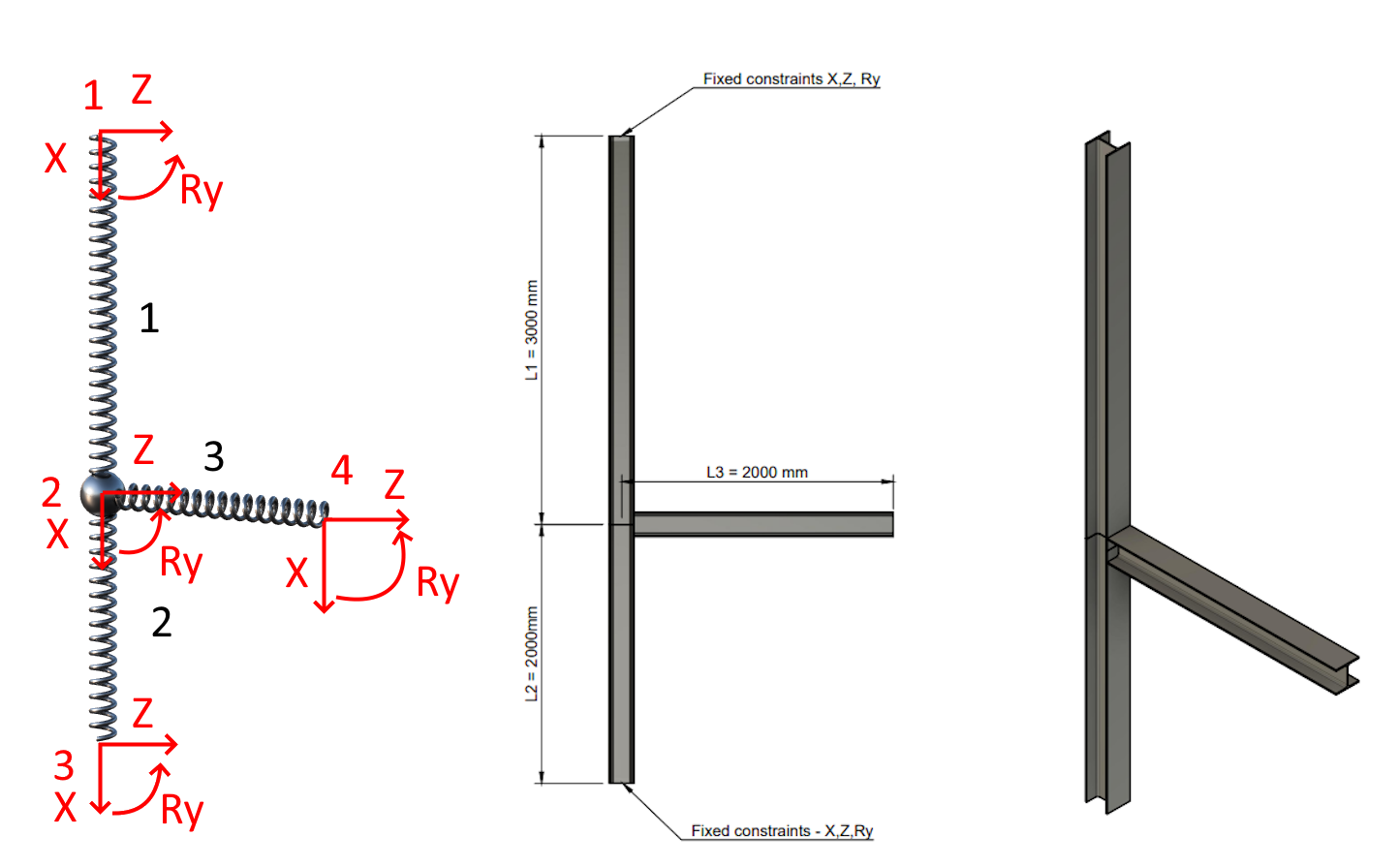
Osserviamo il semplice esempio di una struttura mostrato nella figura 1. La struttura è costituita da una colonna e da un pilastro. La struttura è costituita da una colonna e da una trave con identiche proprietà della sezione trasversale HEA 200. Ogni nodo ha tre gradi di libertà. Ogni nodo ha tre gradi di libertà, tra cui due traslazioni (X e Z) e una rotazione (Ry). Lo spazio di lavoro è 2D. Il materiale è acciaio con un modulo di elasticità di 200.000 MPa.

01) Modello di molla-GCS, geometria, assonometria + sezioni HEA 200

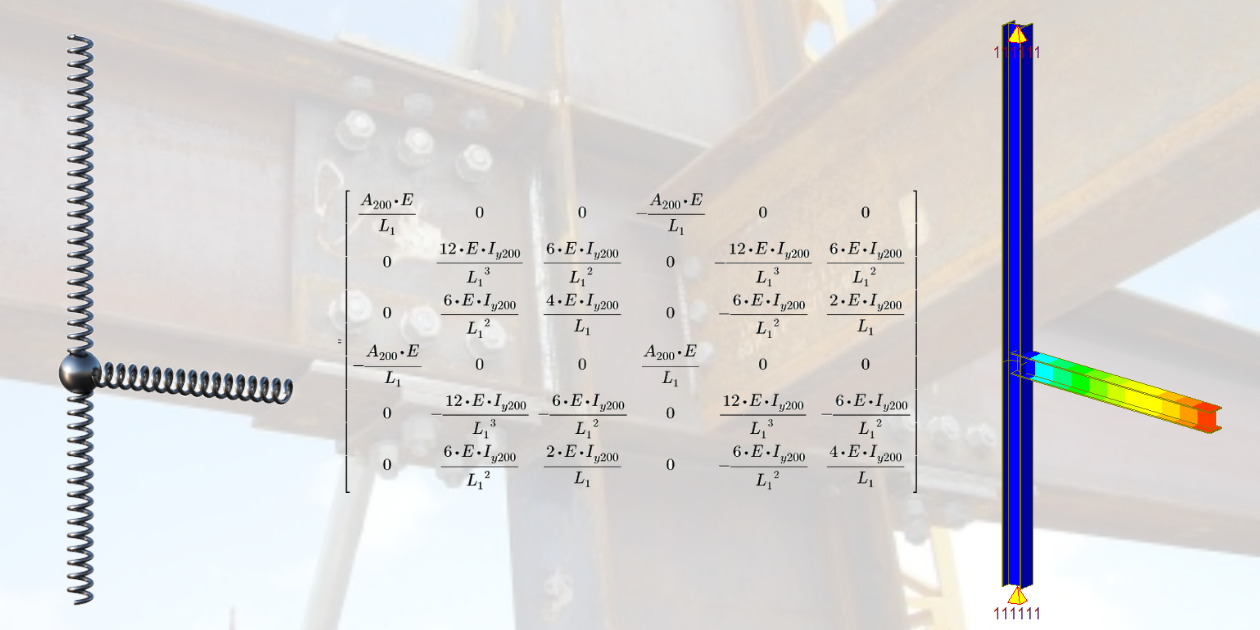
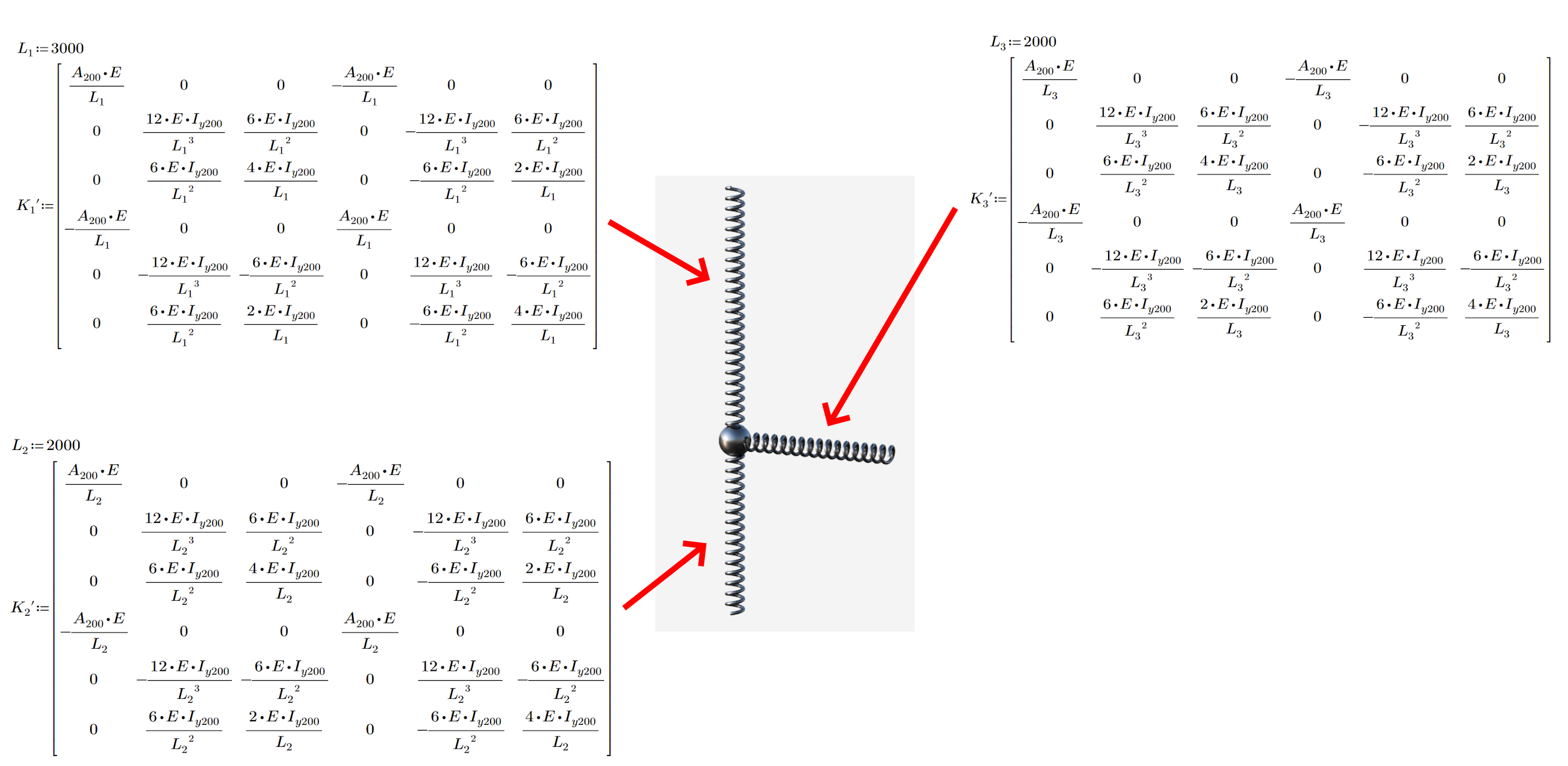
Matrice di rigidità locale

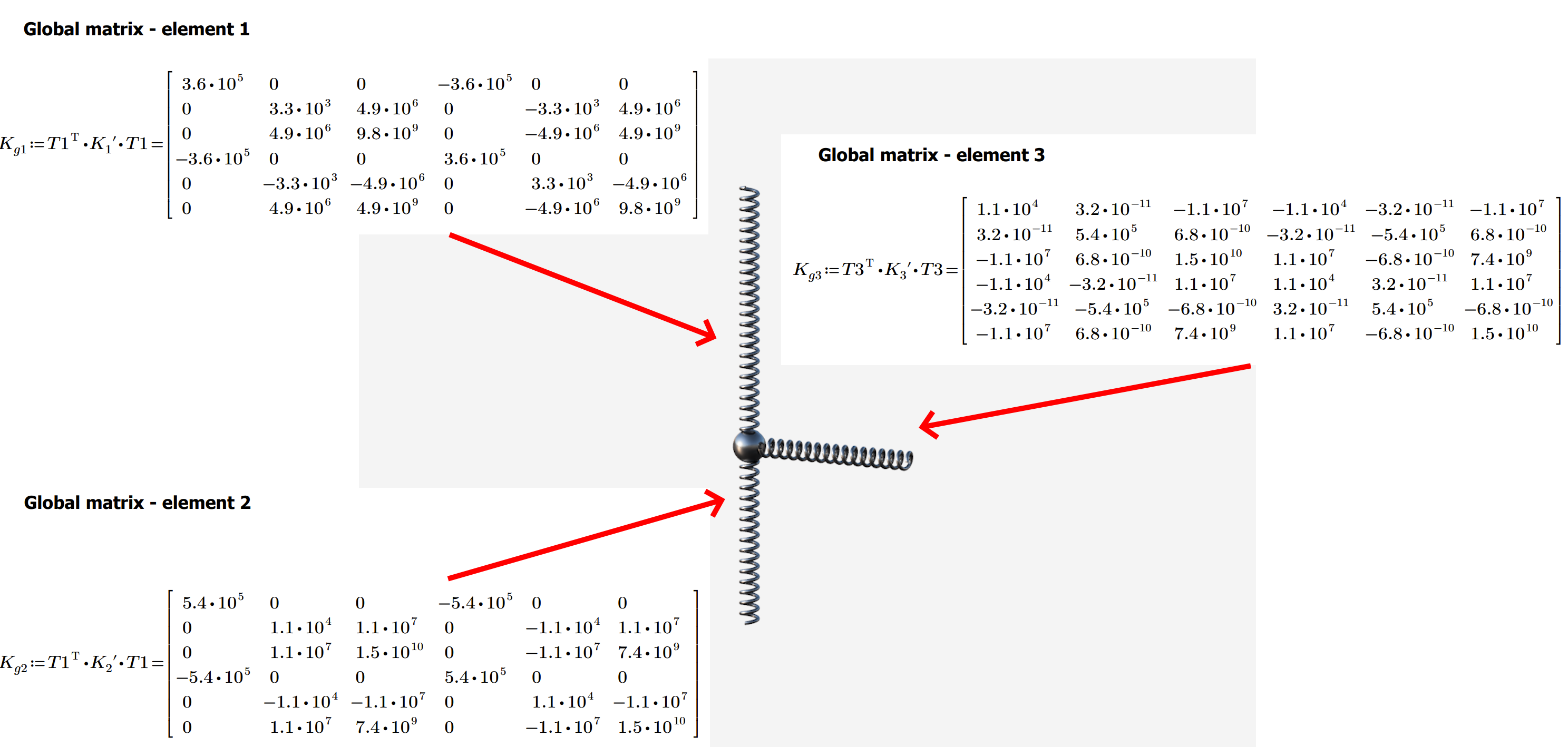
La matrice di rigidità regola la relazione tra la variazione degli spostamenti (e delle rotazioni) alle estremità della trave e le forze (reazioni) corrispondenti. Vale la pena di notare che ogni nodo dell'area di lavoro 2D ha tre gradi di libertà (due traslazioni e una rotazione), il che determina una matrice locale di dimensioni 6x6. Questa matrice rappresenta la rigidità normale, la rigidità a taglio e la rigidità a flessione dell'elemento.

02) Matrice di rigidezza locale di tutti gli elementi

Matrice di trasformazione

Nel 90% delle strutture, la matrice di rigidezza locale delle membrature non è allineata con il sistema di coordinate globale. Solo le travi semplici allineate in linea retta hanno lo stesso sistema di coordinate locali (LCS) e lo stesso sistema di coordinate globali (GCS). Nel nostro caso, il terzo elemento viene ruotato di 90 gradi intorno al nodo due. Questa trasformazione è necessaria per i prossimi calcoli.

03) Matrice di trasformazione membri 1,2; Matrice di trasformazione membri 3

Trasformazione in un sistema di coordinate globale

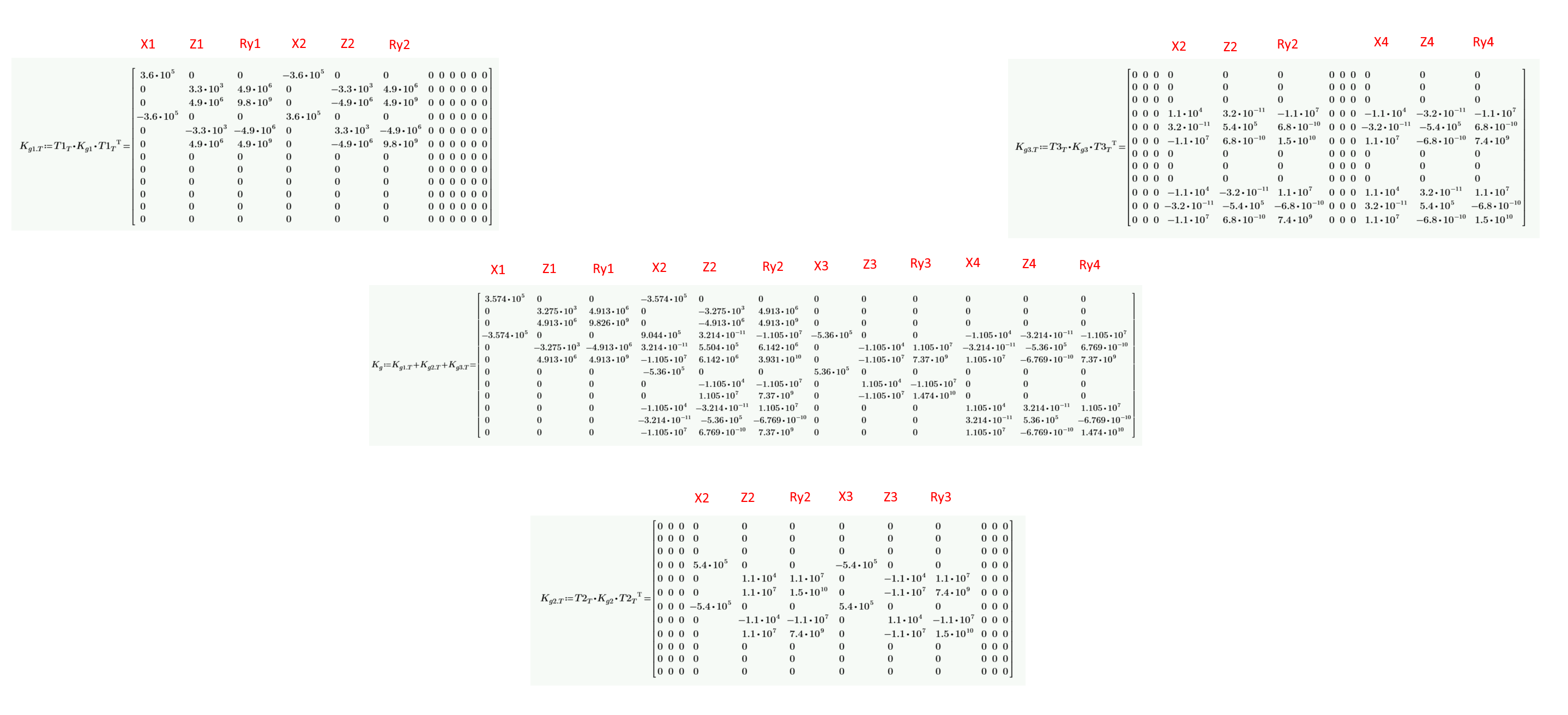
Per un calcolo accurato degli spostamenti, è essenziale allineare i sistemi di coordinate di tutti i membri coinvolti. Un modo per ottenere questo risultato è utilizzare una matrice di trasformazione, che semplifica il processo e consente una transizione agevole al calcolo dello spostamento. La trasformazione non modifica la matrice per i membri uno e due, poiché il loro sistema di coordinate locali è lo stesso di quello globale. Tuttavia, è possibile osservare un cambiamento nel membro tre, che viene ruotato di circa 90 gradi. Le voci per le traslazioni X e Z sono. Si possono notare dei piccoli numeri non nulli nella matrice. Questi derivano dal processo numerico, ma poiché sono relativamente piccoli rispetto alla rigidità complessiva, non influenzano i risultati in modo significativo.

04) Matrice globale membri 1,2; Matrice globale membri 3

Matrice globale - sommatoria

I nodi sono quattro e ogni nodo ha tre gradi di libertà. Ciò significa che la matrice risultante ha dimensioni 12x12. La parte cruciale del processo consiste nel sommare i valori delle colonne e delle righe delle singole matrici in quella globale.

05) Matrice di rigidità globale di tutto il sistema

Condizione limite e vettore di carico

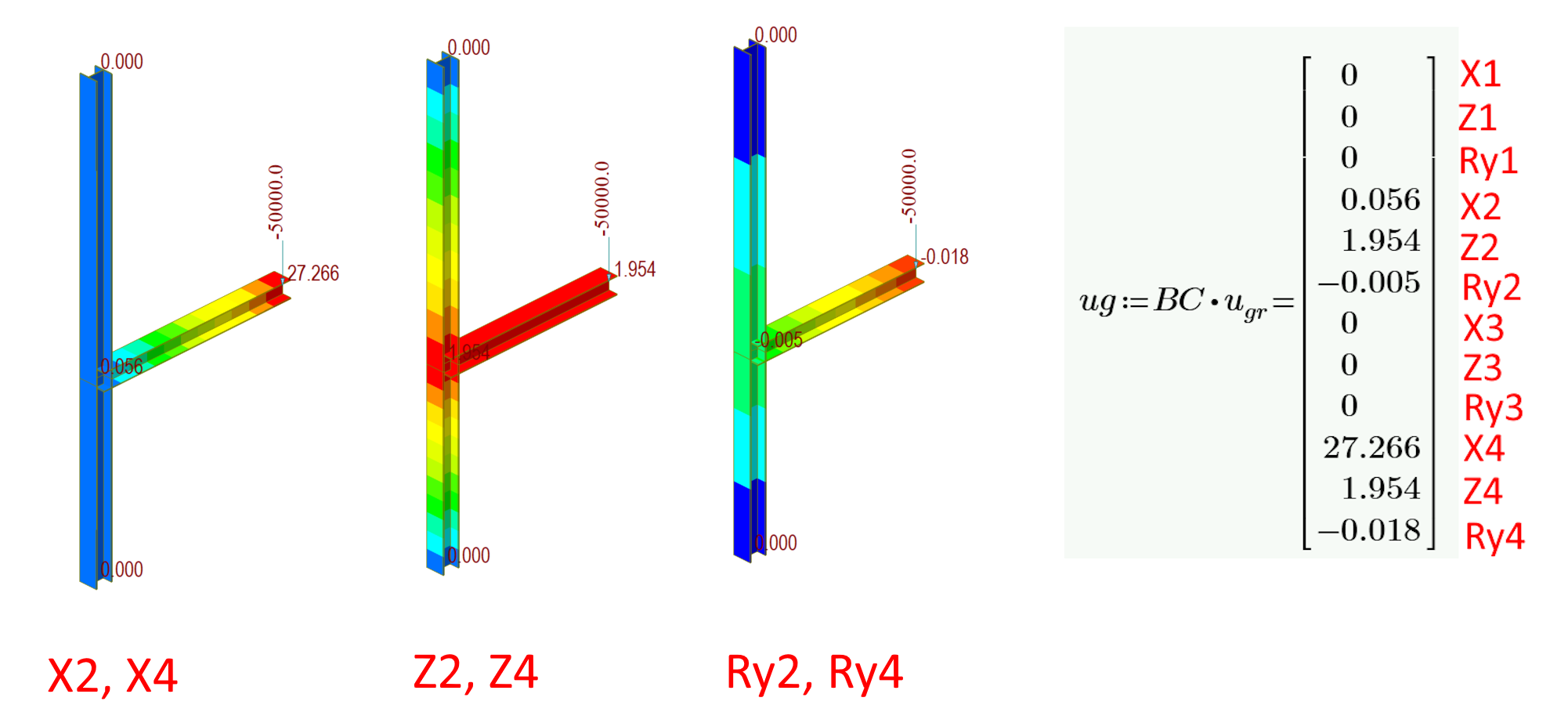
Senza condizioni al contorno, il sistema è sottodeterminato (e si può ottenere solo la soluzione banale). In questo scenario, si considerano vincoli fissi ai nodi uno e tre. Gli spostamenti (e le rotazioni) nulli del contorno possono essere rappresentati eliminando le righe e le colonne corrispondenti. La soluzione è banale se non vengono applicate forze (spostamenti nulli). Nel nostro esempio, il nodo quattro è soggetto a una forza verticale di 50 kN.

06) Matrice ridotta, vettore di carico e condizioni al contorno applicate

Soluzione

Tenendo conto delle piccole deformazioni e del materiale linearmente elastico, possiamo risolvere senza problemi il vettore degli spostamenti sconosciuti in un unico passaggio. Questo approccio è rapido ed efficace e rappresenta un metodo conveniente per risolvere i problemi legati agli spostamenti.

07) Spostamento nodale in GCS

Verifica FEA

Dato che i valori forniti per i nodi sono precisi, è indispensabile che il risultato dell'analisi agli elementi finiti (FEA) corrisponda esattamente a quello dell'approccio di rigidezza diretta (DSA). Questo requisito garantisce che i risultati analitici siano coerenti con il comportamento effettivo del sistema studiato. Pertanto, è fondamentale garantire che i risultati FEA e DSA corrispondano entro un livello di tolleranza accettabile.

08) Verifica e confronto degli spostamenti nodali tra DSA e FEA

Approccio di rigidità diretta - connessioni semirigide

È fondamentale comprendere che le connessioni sono tipicamente semirigide e non completamente rigide o simili a perni. Trascurare la rigidezza di una connessione potrebbe far sì che il comportamento di una struttura in un modello sia diverso da quello di una struttura reale. Approfondiamo il modo in cui la rigidità viene presa in considerazione durante i calcoli e come influisce sul comportamento della struttura stessa.

Molla rotazionale e strutture civili

Le strutture civili in acciaio, come capannoni e telai, sono progettate per resistere ai carichi di flessione trasferiti in modo efficiente dalle travi. Quando la trave è caricata e la struttura è iperstatica, la rigidità rotazionale del giunto gioca un ruolo cruciale nel garantire una corretta ridistribuzione del carico e una deformazione precisa. Per questo motivo è importante mantenere l'integrità strutturale del giunto per evitare potenziali danni alla struttura.

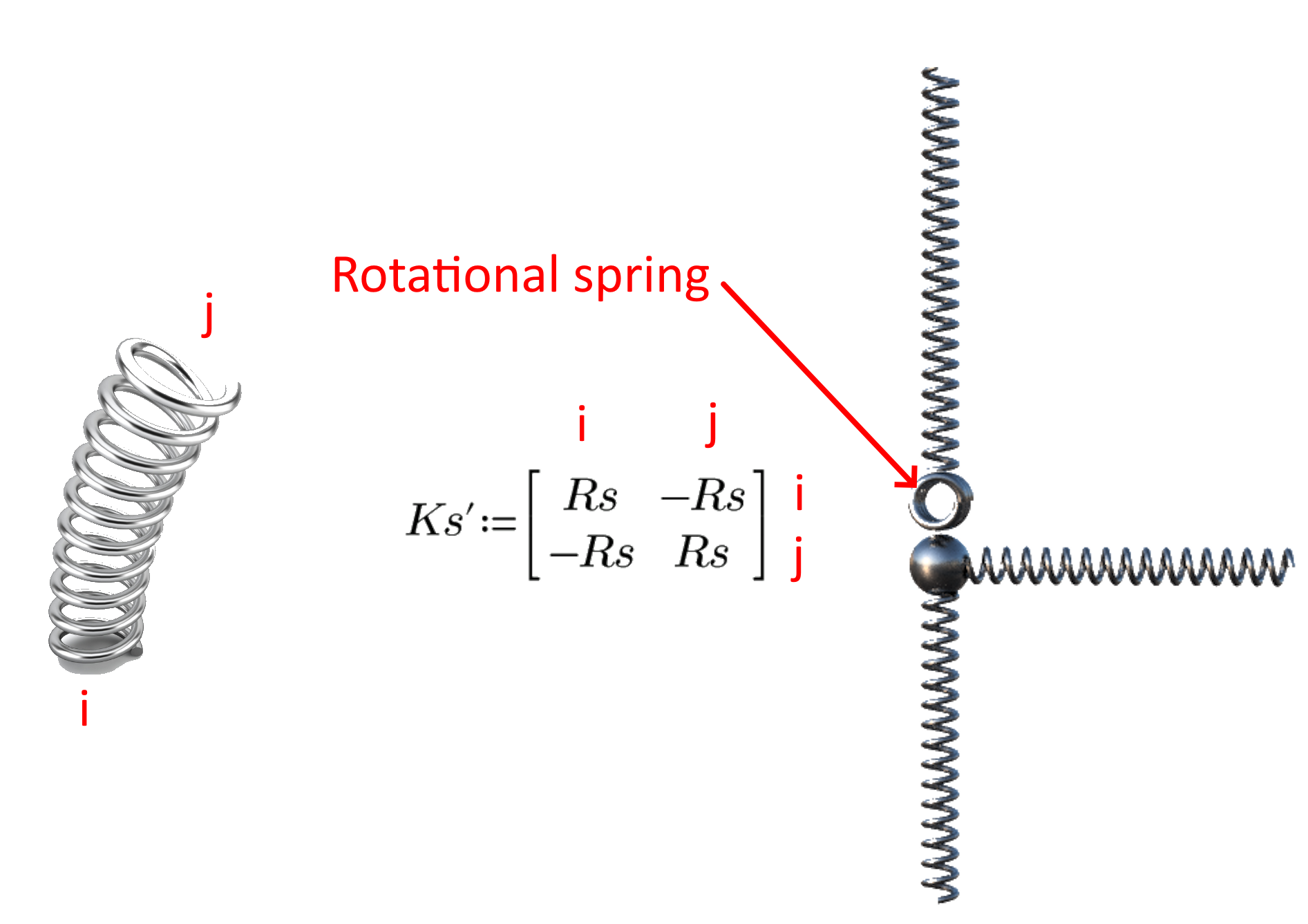
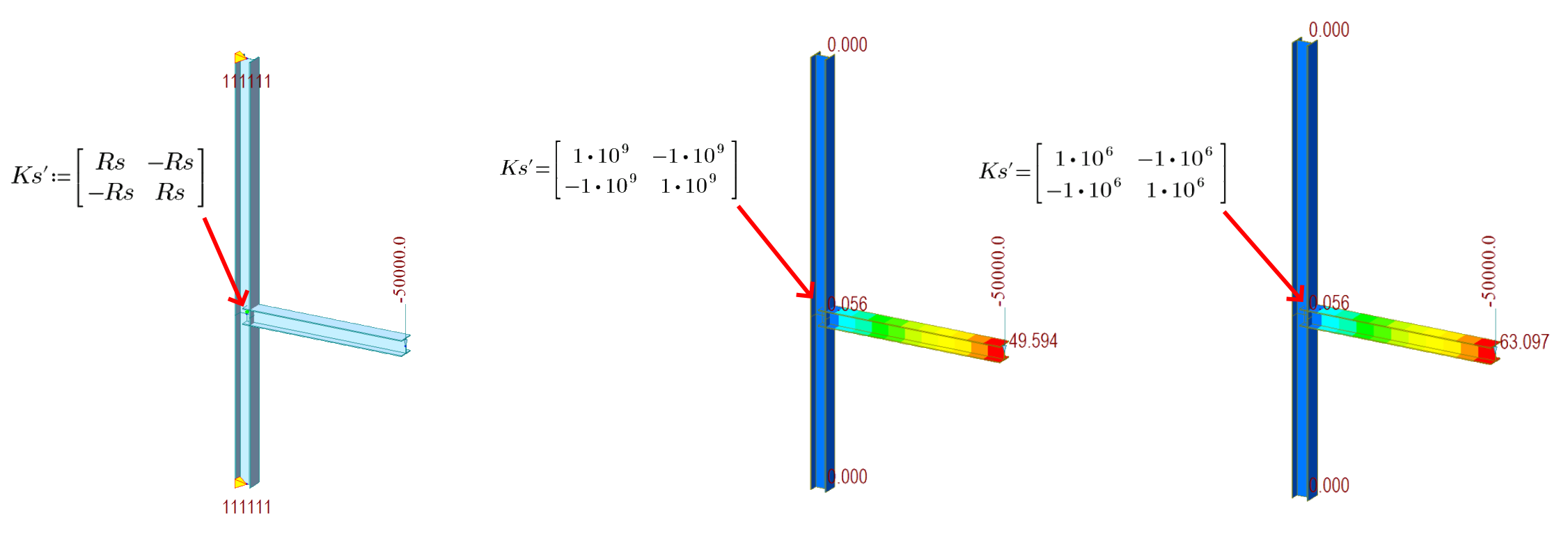
09) Molla rotazionale - matrice locale

Per garantire la compatibilità in un giunto, è importante accoppiare le deformazioni. Questo accoppiamento deve essere incluso nella matrice di rigidità globale per calcolare le deformazioni. Quando si applica la rigidità rotazionale, gli altri gradi di libertà devono essere inclusi come un'altra riga e colonna nella matrice di rigidità globale. La matrice finale per questo tipo di giunto avrà una dimensione di 13x13, mentre una matrice di connessione rigida avrà una dimensione di 12x12.

Impatto della rigidità rotazionale

La rigidità rotazionale di una struttura ha un impatto significativo sulla distribuzione delle forze e sulle deformazioni. Ciò significa che una struttura con rigidità rotazionale si comporterà in modo diverso rispetto a una struttura con connessioni rigide o a perno. Se la rigidità viene aumentata in modo sproporzionato, può portare a ulteriori cambiamenti nel comportamento della struttura. In questo scenario esploreremo gli effetti dell'aumento della rigidità rotazionale. Il modello con cui lavoriamo è quello del capitolo precedente e la molla rotazionale è collegata all'estremità (j) dell'elemento uno.

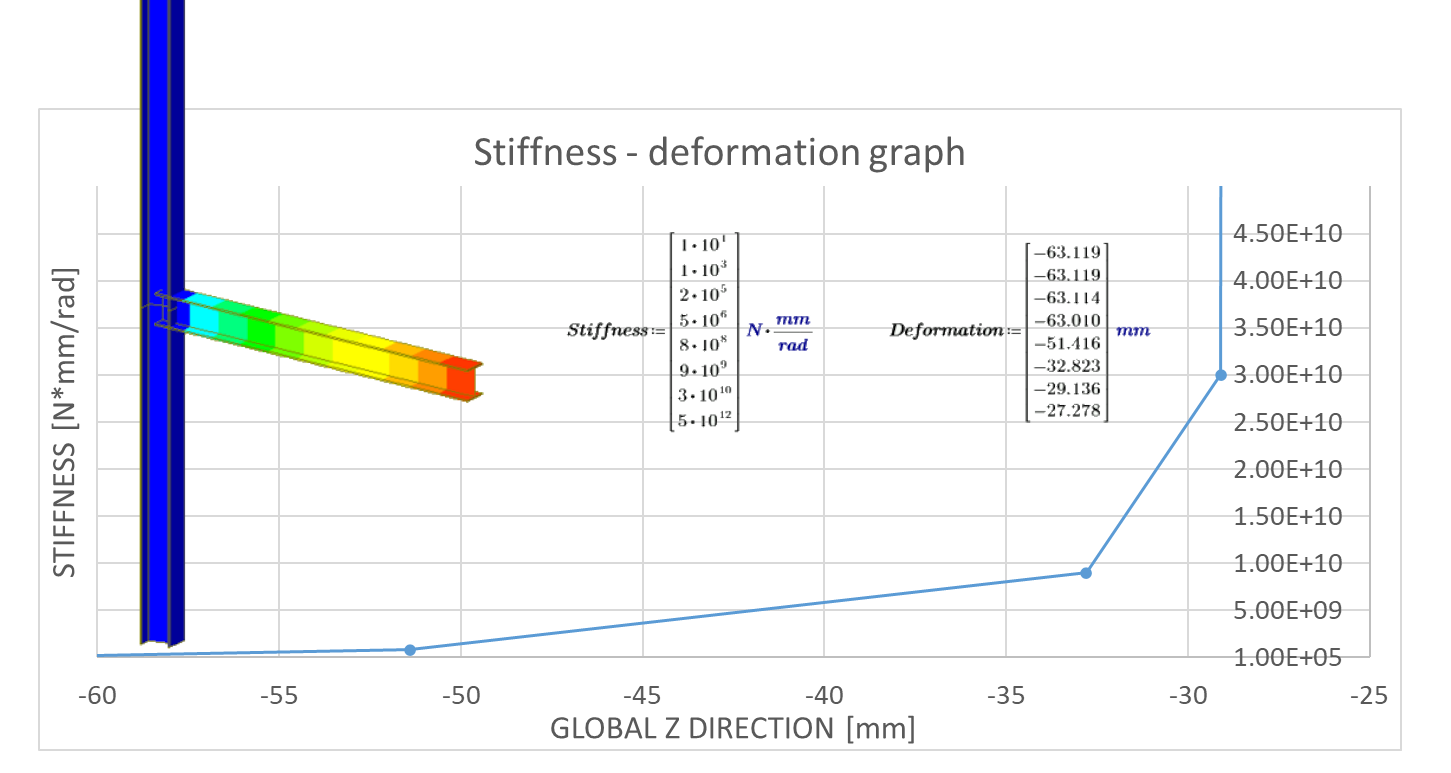
10) Deformazioni per diverse rigidità rotazionali

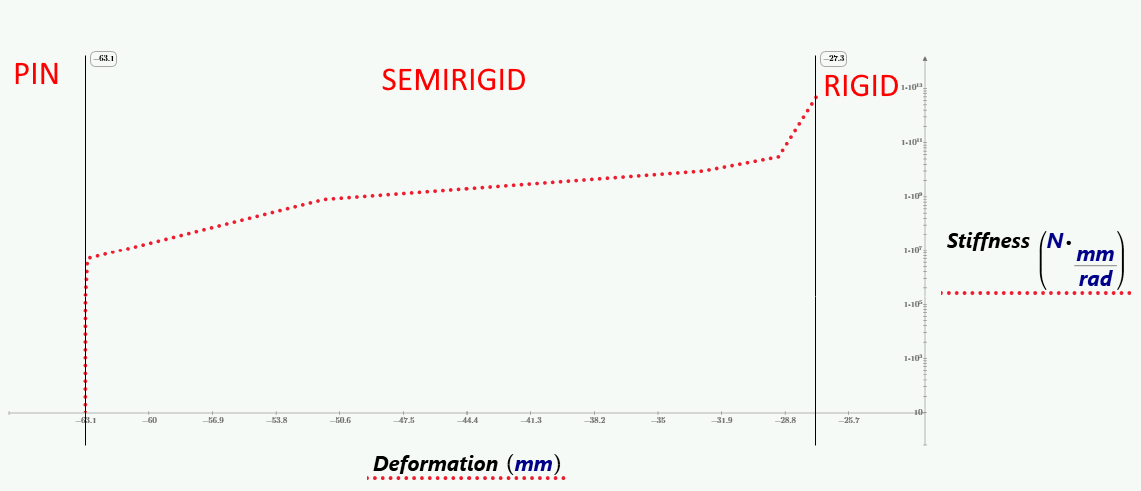
Il grafico indica che, in determinati intervalli di rigidezza, la deformazione cambia in modo multilineare per una connessione semirigida. Per le connessioni semirigide, la sottostima o la sovrastima della rigidezza porta a una significativa differenziazione delle deformazioni e alla ridistribuzione delle forze interne.

11) Grafico rigidezza-deformazione

12) Zona di rigidezza per le connessioni

Conclusione e prossimi argomenti

Per garantire il successo del nostro prossimo studio, è necessario innanzitutto comprendere a fondo il problema in questione. Solo allora potrete procedere con fiducia e determinazione. Il nostro studio è dedicato all'esplorazione di una serie di argomenti importanti che sono rilevanti per la questione che stiamo indagando. Attraverso un'attenta ricerca e analisi, ci auguriamo di gettare nuova luce su questo problema complesso e impegnativo e di contribuire, in ultima analisi, a una migliore comprensione di questa importante area di studio.

• Come si calcola la rigidezza rotazionale in IDEA StatiCa
• Come utilizzare la rigidezza per più membri in uno strumento FEA
• Verifica della rigidezza rotazionale tra IDEA StatiCa e ABAQUS per una connessione piastra-piastra