Fillet weld in angle plate joint

Description

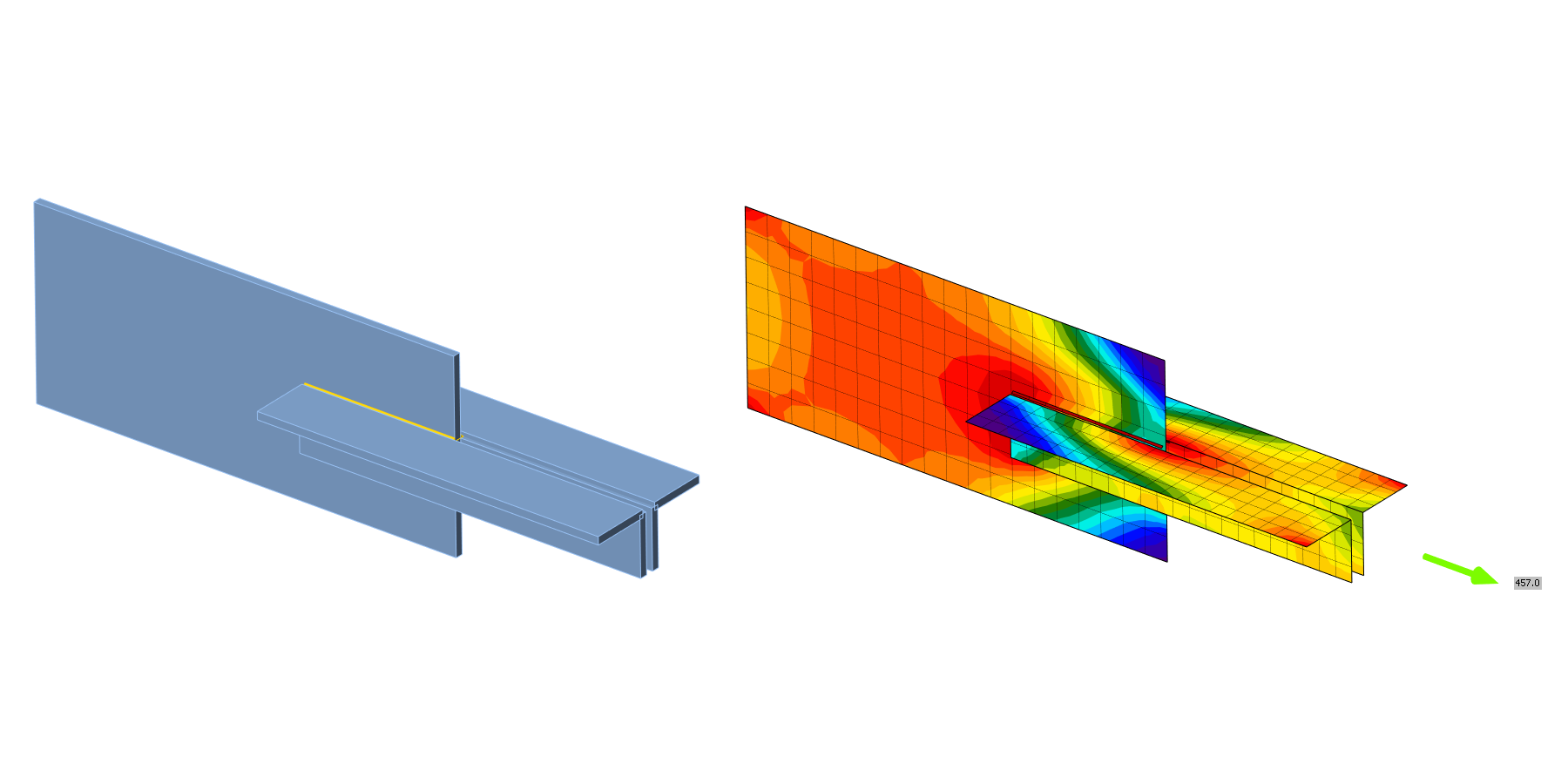
In this chapter, the model of the fillet weld in angle plate joint calculated by component-based finite element method (CBFEM) is verified on component method (CM). An angle is welded to a plate and loaded by normal force. The angle size and the length of the weld are studied in a sensitivity study.

Analytical model

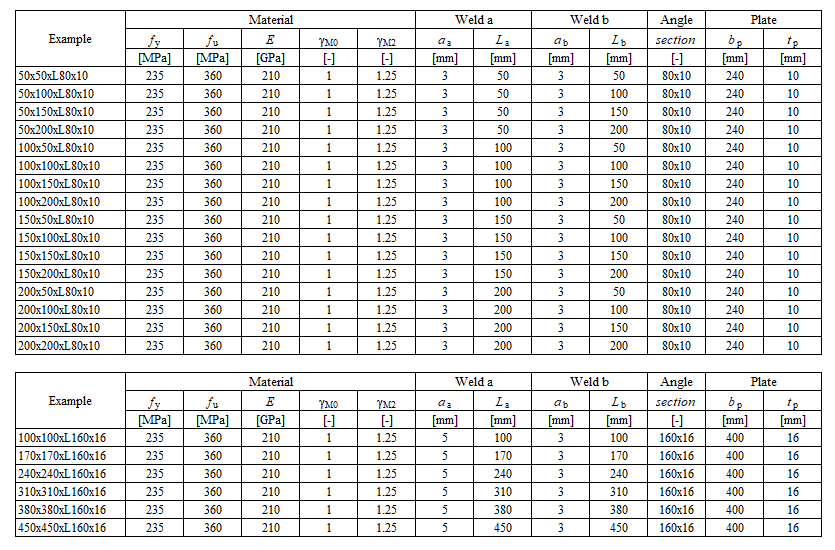
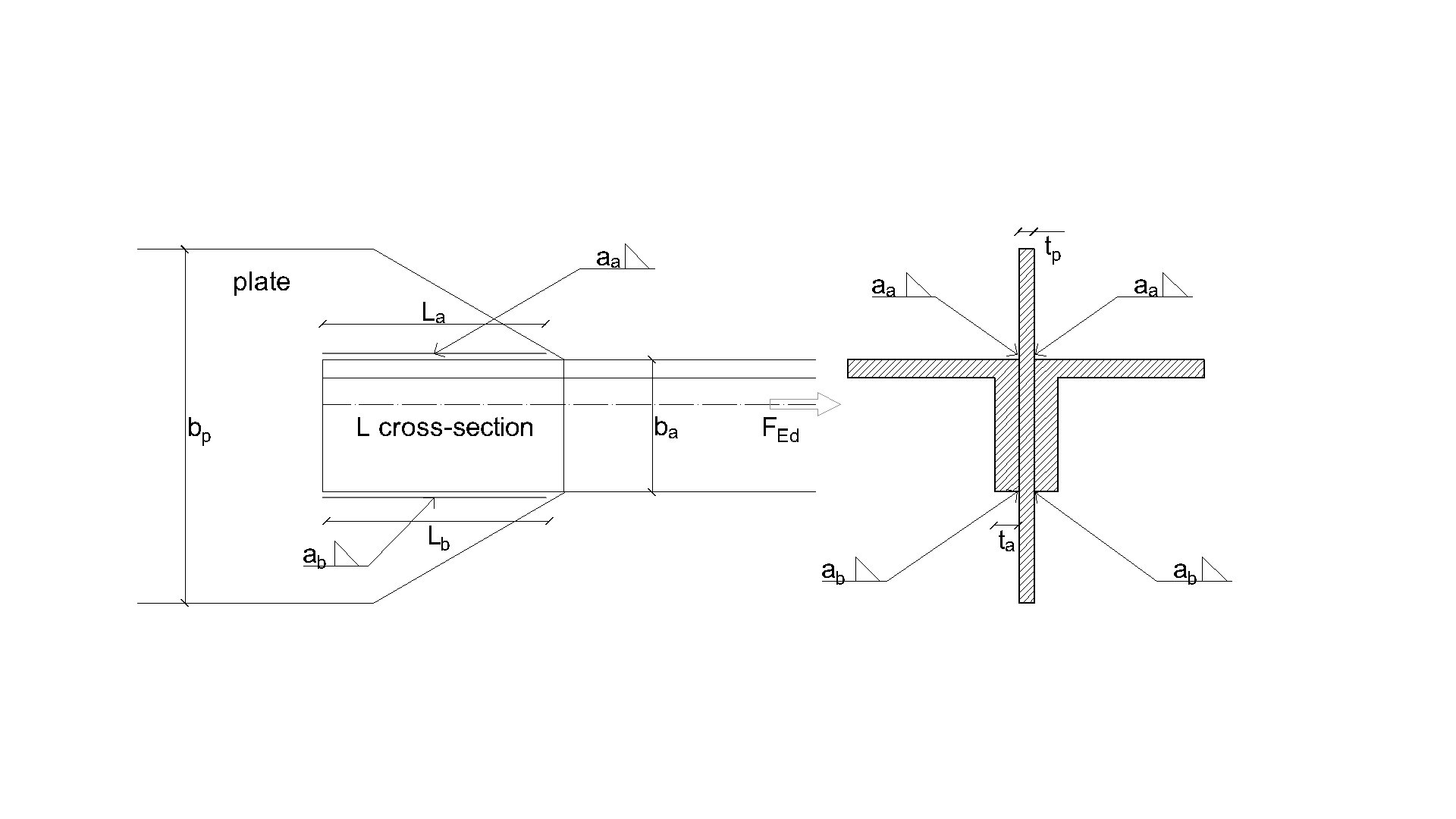
The fillet weld is the only component examined in the study. The welds are designed according to Chapter 4 in EN 1993-1-8:2005 to be the weakest component in the joint. The design resistance of the fillet weld is described in Section 4.1. Overview of considered examples and material is given in Tab. 4.2.1. The geometry of the joints with dimensions is shown in Fig. 4.2.1.

Component method calculation 

This hand calculation neglects the additional moment of the weld, which is developed due to force redistribution to the L cross-section parts acc. to EN 1993-1-8 (4.13).

\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[\sigma_{\perp} = \tau_{\perp} = 0 \]

\[ \tau_{\parallel} = \frac{V}{l  \cdot  a}\]

\[ \sqrt{  3 \cdot \left( \tau_{\parallel} \right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[ \sqrt{  3 \cdot \left(  \frac{V}{l \cdot a}\right)^2} \leq \frac{f_u}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[ V = \frac{f_u  \cdot  l \cdot  a  \cdot  \beta_{\mathrm{Lw1}}}{\beta_{\mathrm{w}}  \cdot  \gamma_{\mathrm{M2}}  \cdot  \sqrt{3}} \]

Total resistance calculated as sum of top and bottom weld resistances 

\[ V = V_\mathrm{top} + V_\mathrm{bottom} \]

Where:

\(a\) - weld throat thickness

\(V\) - shear force acting on beam

\(l = 2 \cdot L_\mathrm{\dots}\) - parallel welds length

\(\beta_{\mathrm{w}}\) - correlation factor taken from EN 1993-1-8 Table 4.1

\(\beta_{\mathrm{Lw1}}\) - long weld reduction factor, EN 1993-1-8 Equation 4.9

\(f_u\) - nominal ultimate tensile strength of the weaker part joined

\(\gamma_{\mathrm{M2}}\) - partial safety factor for welds

\[ \textsf{\textit{\footnotesize{Tab. 4.2.1 Examples overview}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.2.1 Joint geometry with dimensions}}}\]

Numerical model

The weld component in CBFEM is described in General theoretical background and EN theoretical background. The weld model has an elastic-plastic material diagram, and stress peaks are redistributed along the weld length.

Verification of resistance

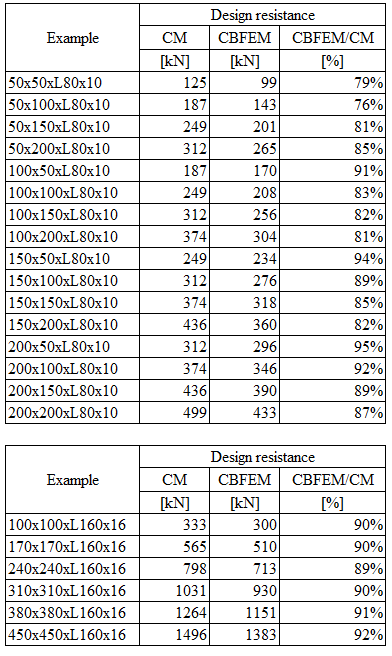
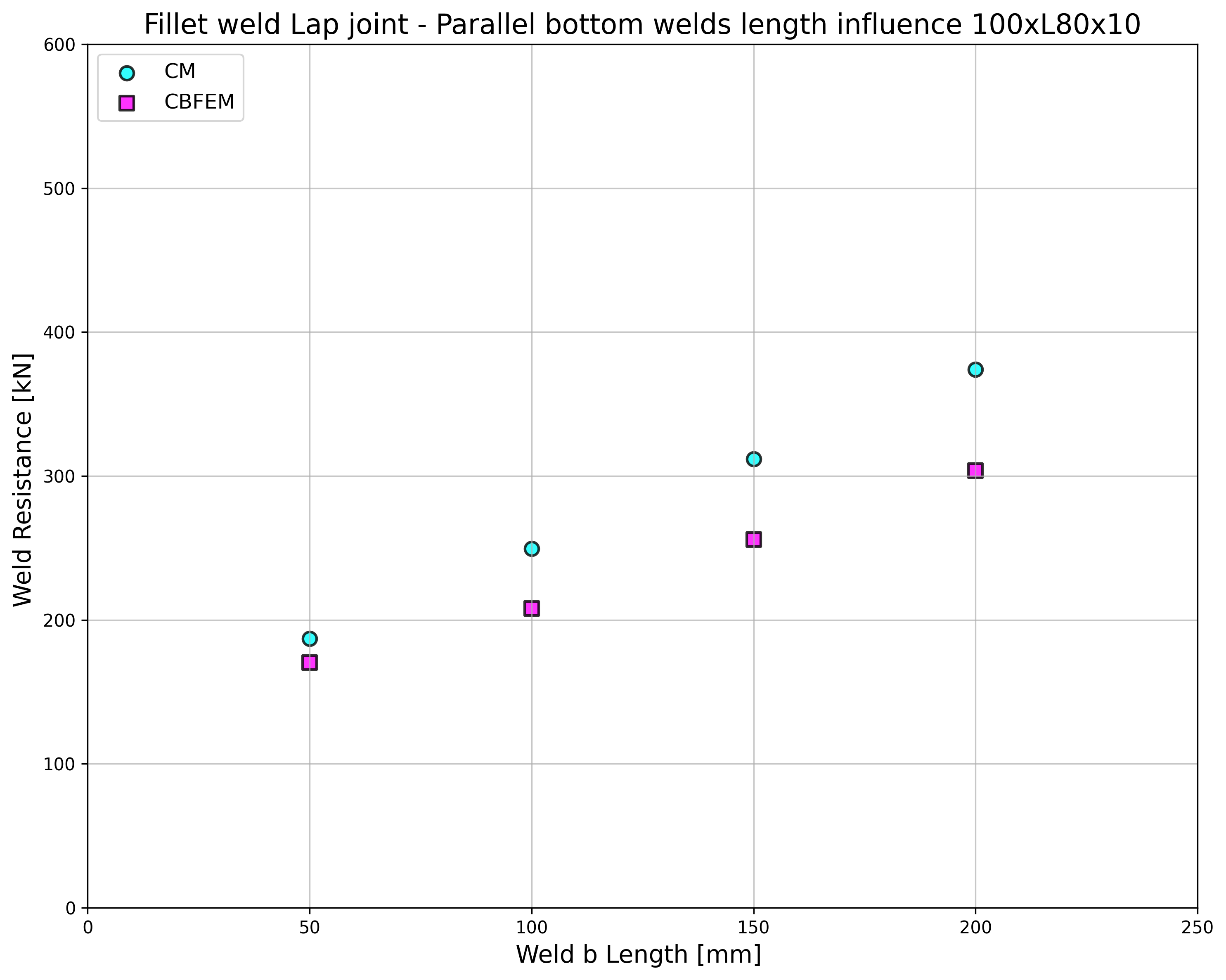
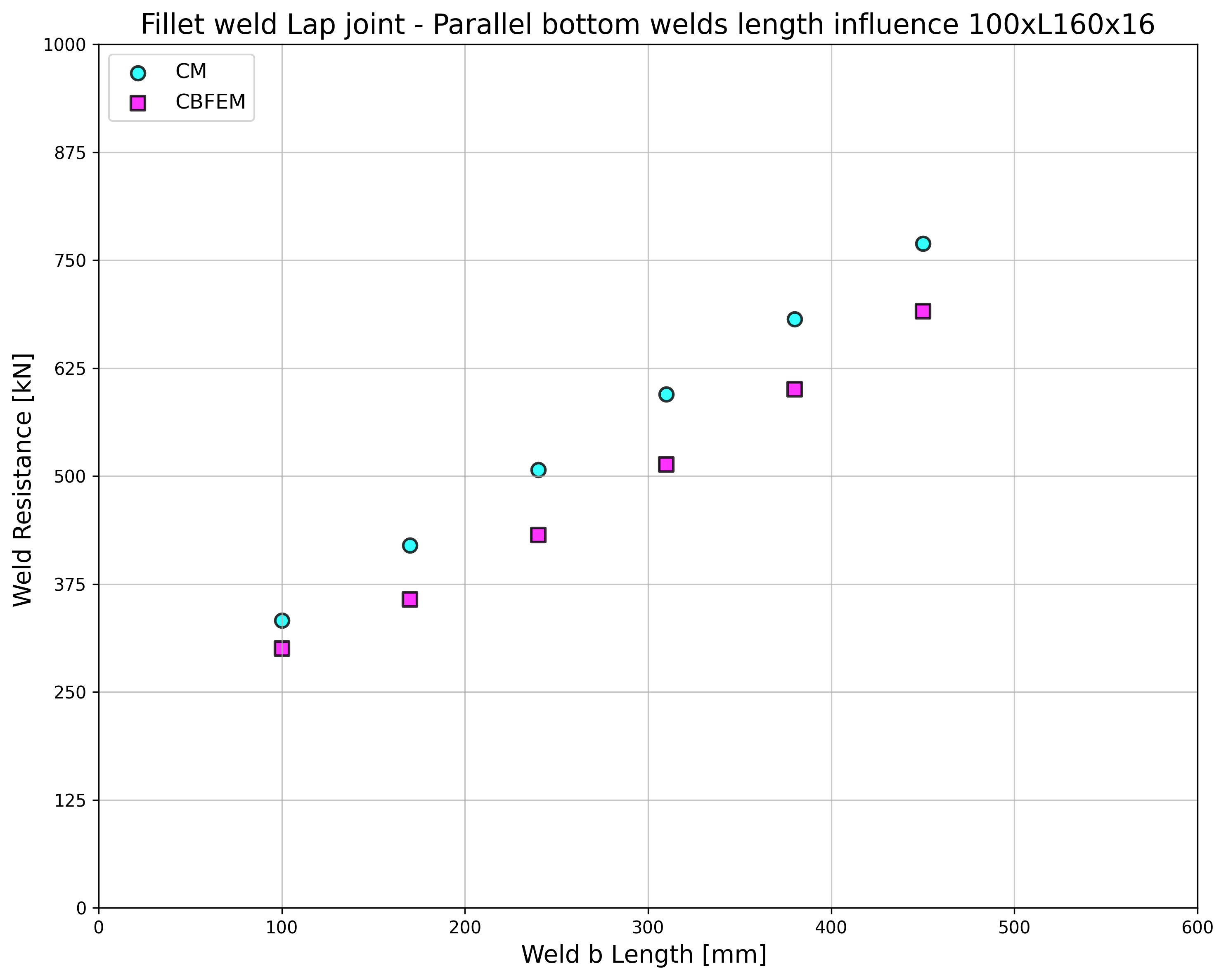
The weld design resistances calculated by CBFEM are compared with the results of CM; see Tab. 4.2.2. Two parameters are studied: the length of the weld and the angle section. Fig 4.2.2 shows the sensitivity study of bottom weld  length. The length of the top weld a  in the study is L_a=100mm.

 \[ \textsf{\textit{\footnotesize{Tab. 4.2.2 Comparison of CBFEM and CM}}}\]

\[ \textsf{\textit{\footnotesize{a}}}\]

\[ \textsf{\textit{\footnotesize{b}}}\]

\[ \textsf{\textit{\footnotesize{a) Angle cleat 80×10             b) Angle cleat 160×16}}}\]

 \[ \textsf{\textit{\footnotesize{Fig. 4.2.2 Sensitivity study of bottom weld b length}}}\]

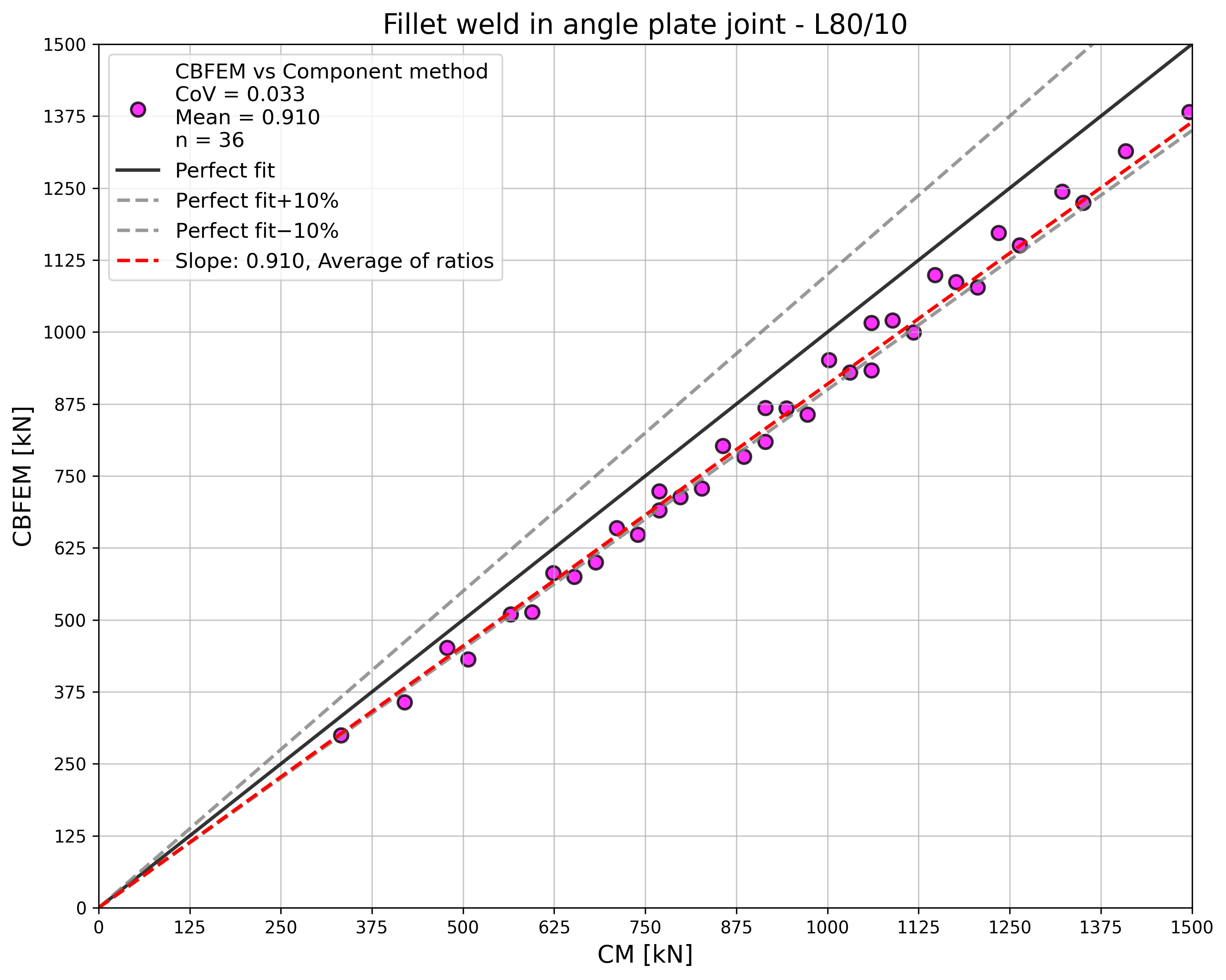
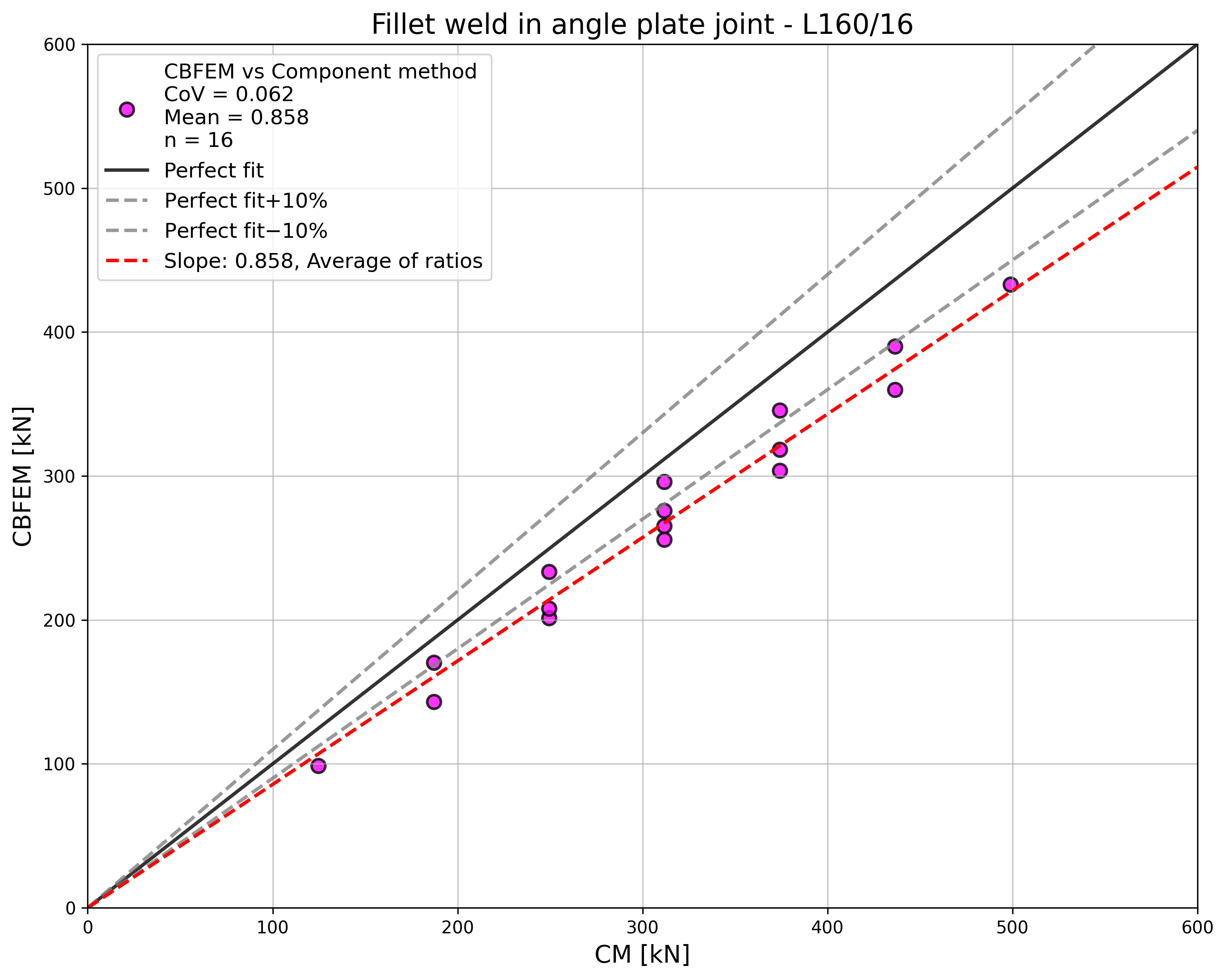
Results of CBFEM and CM are compared, and the sensitivity study is presented. The influence of weld length on the design resistance of a welded angle joint is shown in Fig. 4.2.2. The study shows good agreement for all weld configurations. To illustrate the accuracy of the CBFEM model, the results of the study are summarized in a diagram comparing design resistances by CBFEM and CM; see Fig. 4.2.3. The results show that all the predictions of CBFEM are safe-sided compared to the CM, where eccentricity is neglected.

\[ \textsf{\textit{\footnotesize{Fig. 4.2.3 Verification of CBFEM to CM}}}\]

Benchmark example

Inputs

Angle

• Cross-section 2×L80×10
• Distance between angles 16 mm

Plate

• Thickness t_p = 16 mm
• Width b_p  = 240 mm

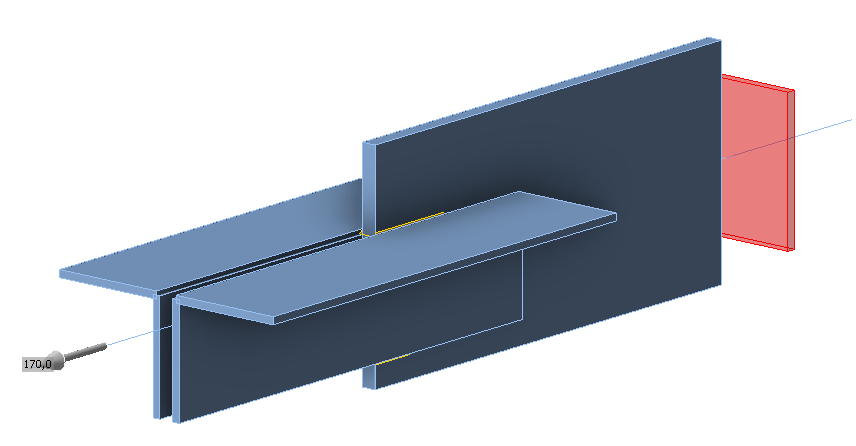
Weld, parallel fillet welds, see Fig. 4.2.4

• Throat thickness a_w  = 3 mm
• Top weld length L_w,top = 100 mm
• Bottom weld length L_w,bottom = 50 mm

Outputs

• Design resistance in tension F_Rd = 170 kN (It should be noted that the resistance was calculated using the "Stop at limit strain" function. Consequently, the actual CBFEM resistance may be marginally higher.)

\[ \textsf{\textit{\footnotesize{Fig. 4.2.4 Benchmark example of the welded angle plate joint with parallel fillet welds}}}\]