Parete a taglio con aperture sfalsate

La funzione principale delle pareti di taglio è quella di resistere ai carichi laterali che si verificano durante terremoti, tempeste di vento o altri eventi dinamici. Trasferendo le forze alle fondamenta dell'edificio, le pareti a taglio aiutano a minimizzare i danni strutturali e a mantenere l'integrità della struttura. Le pareti a taglio sono posizionate strategicamente all'interno della pianta di un edificio per garantire un'efficace distribuzione dei carichi laterali. Di solito si trovano sul perimetro dell'edificio o vicino al suo nucleo. Nei grattacieli, le pareti a taglio sono spesso situate intorno ai vani degli ascensori e delle scale per garantire maggiore rigidità e stabilità. Le pareti a taglio offrono diversi vantaggi, tra cui una maggiore stabilità strutturale, una migliore resistenza ai carichi laterali e una maggiore sicurezza generale durante gli eventi sismici. Inoltre, le pareti a taglio possono contribuire al design architettonico, offrendo opportunità di espressione creativa pur svolgendo la loro funzione strutturale.

Descrizione del modello

Per la valutazione dei risultati sono stati definiti quattro modelli di verifica. Due di questi modelli considerano le proprietà caratteristiche del materiale, mentre gli altri due si basano sui valori di progetto secondo l'Eurocodice 1992-1-1[3]. Questi modelli di verifica si basano sulla teoria del campo di sollecitazione compatibile (CSFM)[1] e sul modello di plasticità Drucker-Prager[2].

Per una migliore comprensione, si prega di notare la seguente identificazione del modello:

• Detail - Caratteristica
• Detail - Progetto
• ABAQUS - Caratteristica
• ABAQUS - Progettazione

Geometria e materiali

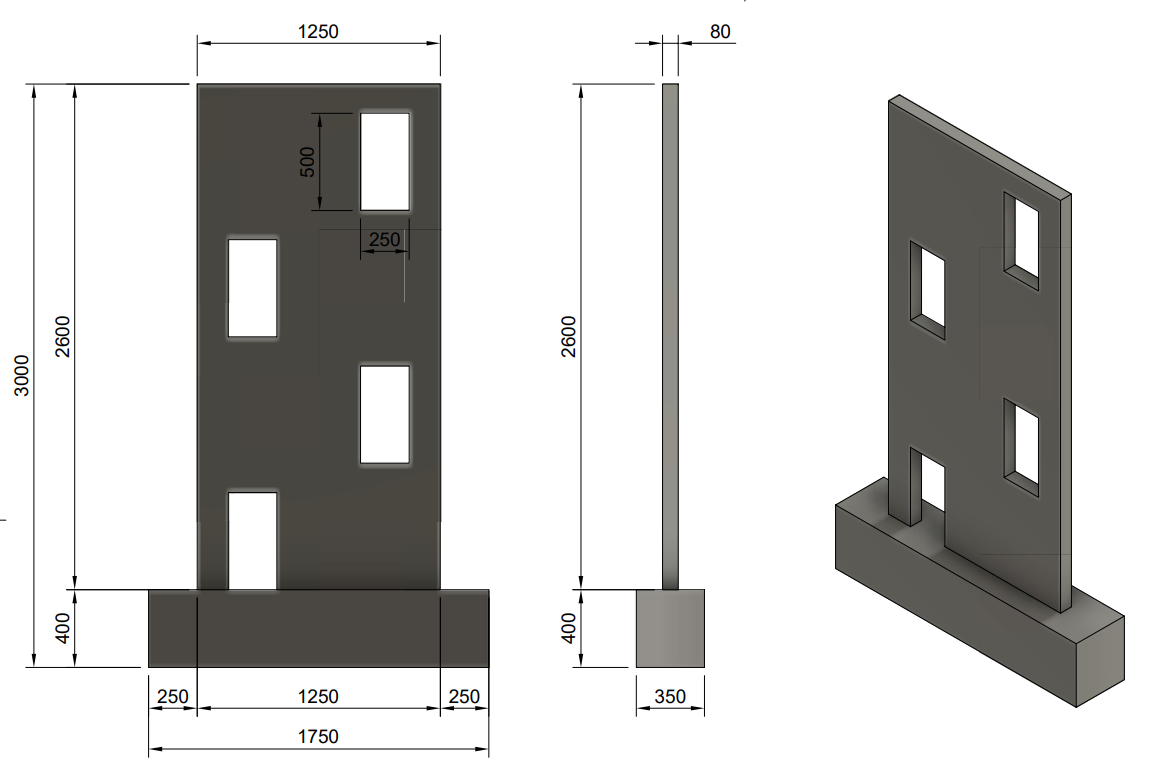
Il modello di prova è stato ridotto di quattro volte rispetto alle dimensioni reali. Le fondazioni della struttura misurano 1750 mm x 400 mm x 350 mm, mentre le pareti hanno dimensioni di 1250 mm x 2600 mm x 80 mm. Le pareti sono suddivise in quattro livelli con aperture sfalsate, ciascuna delle quali misura 250 mm x 500 mm. Il calcestruzzo utilizzato è di grado C35/45 ed è armato con B500B e un diametro di 6 mm. I carichi sono trasferiti mediante piastre aggiuntive in acciaio strutturale S235.

Fig. 1) Geometria

Metodo del campo di sollecitazione compatibile

Assunzioni

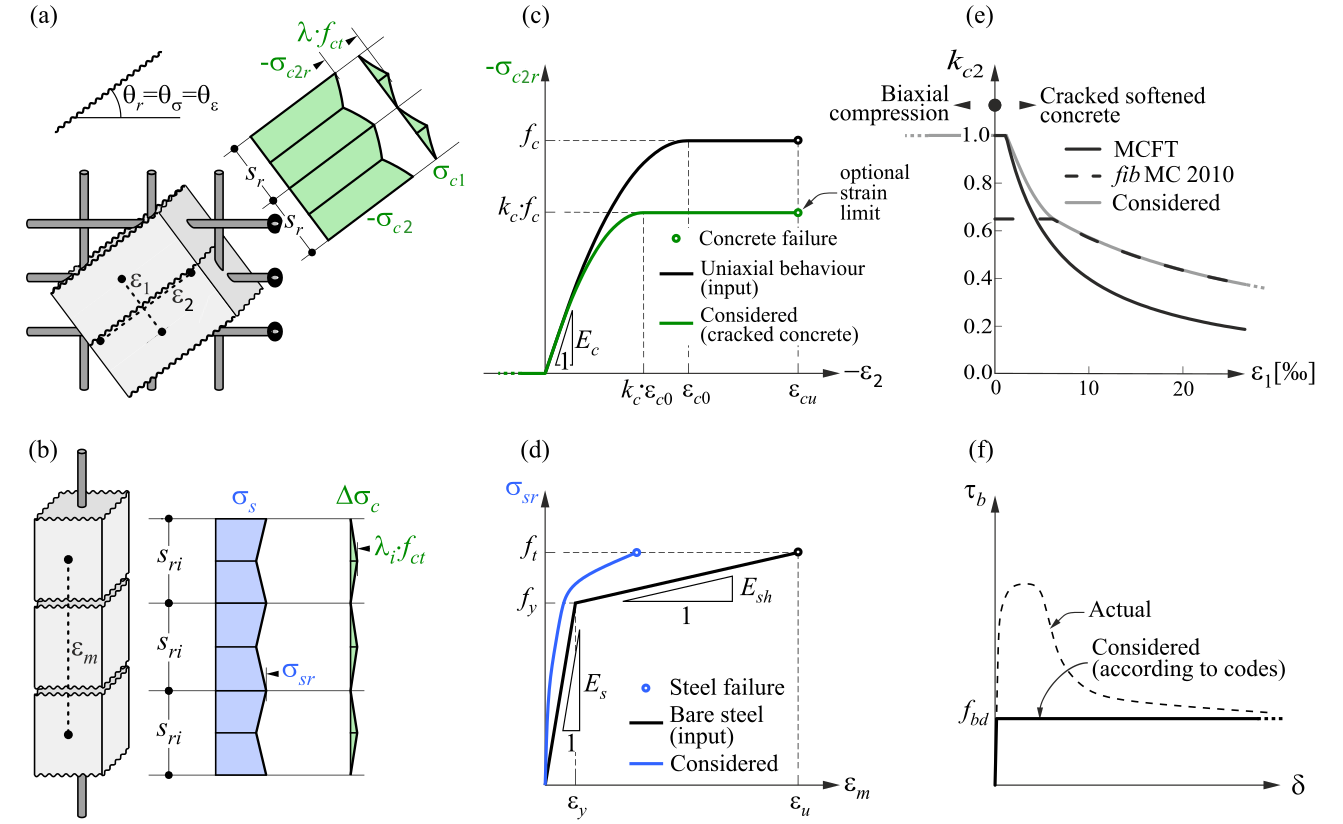
Il CSFM considera la massima sollecitazione principale del calcestruzzo in compressione (_σc2r) e le sollecitazioni dell'armatura (_σsr) in corrispondenza delle fessure, trascurando la resistenza a trazione del calcestruzzo (_σc1r = 0), ad eccezione del suo effetto di irrigidimento sull'armatura. La considerazione dell'irrigidimento a trazione consente di simulare le deformazioni medie dell'armatura (_εm). Maggiori informazioni sulla teoria sono disponibili in Background teorico.

Fig. 2) Metodo del campo di sollecitazione compatibile - Assunzioni

Modello di plasticità Drucker-Prager (DPPM)

Ipotesi

La plasticità del calcestruzzo (in seguito CDP) si basa sulla condizione di plasticità di Drucker-Prager. Questo modello è adatto a materiali con attrito interno, come il terreno o il calcestruzzo. La resistenza alla trazione è inferiore alla resistenza alla compressione e la parte idrostatica del tensore delle sollecitazioni gioca un ruolo nell'evoluzione della superficie di plasticità. In condizioni di sollecitazione generale, la condizione di plasticità ha la superficie di un cono rotante. Il modello dei materiali per le sollecitazioni di compressione e trazione considera anche il comportamento post-critico, che è controllato dai cosiddetti parametri di danno, che assumono valori da zero a uno (per una rigidità elastica prossima allo zero del calcestruzzo in compressione o in trazione nella condizione post-critica). Più grande è il numero del parametro di danno, più l'elemento è violato e non contribuisce al contributo di rigidezza.

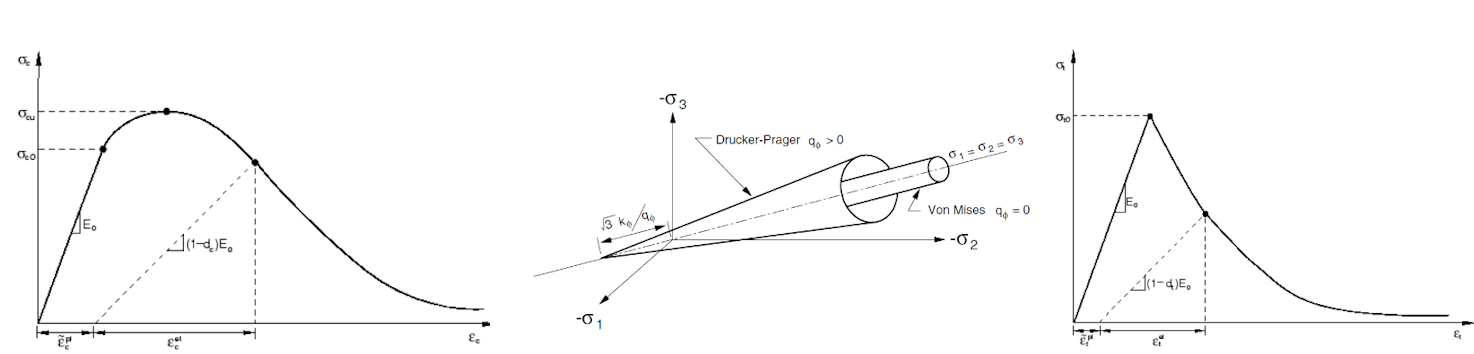
Il modello di materiale uniassiale in compressione e tensione per il calcestruzzo si basa sulla teoria di Thorenfeldt[4]. Tutti gli input sono valori di progetto che seguono l'approccio di affidabilità della norma EN 1992-1-1[3]. Il modello materiale dell'armatura B500B è considerato con irrigidimento a trazione. Ulteriori informazioni sulla teoria.

Fig. 3) Modello del materiale in compressione (a sinistra), superficie di plasticità Drucker-Prager (al centro), modello del materiale in trazione (a destra)

Modelli numerici

Metodo del campo di sollecitazione compatibile - IDEA StatiCa Detail

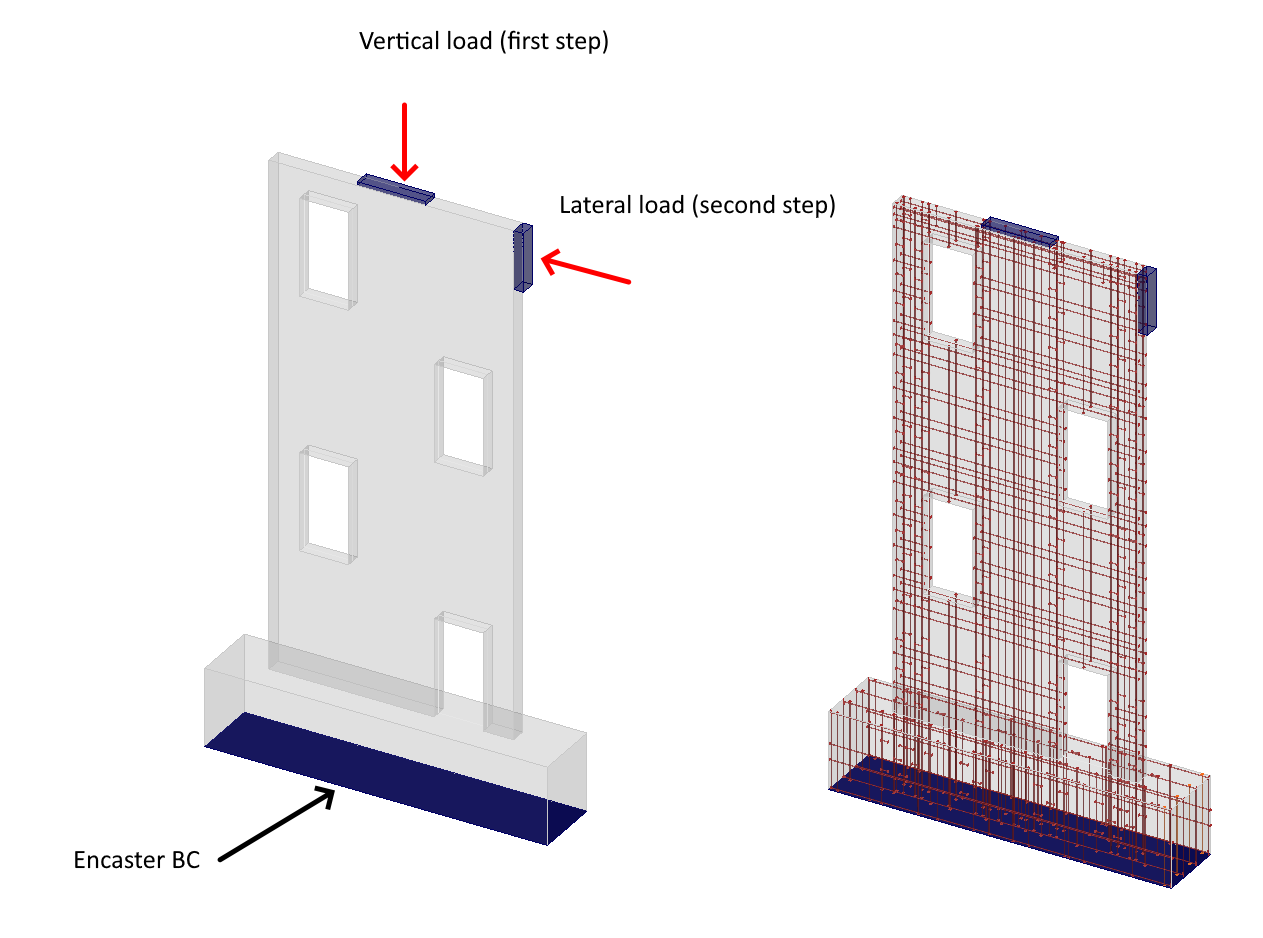
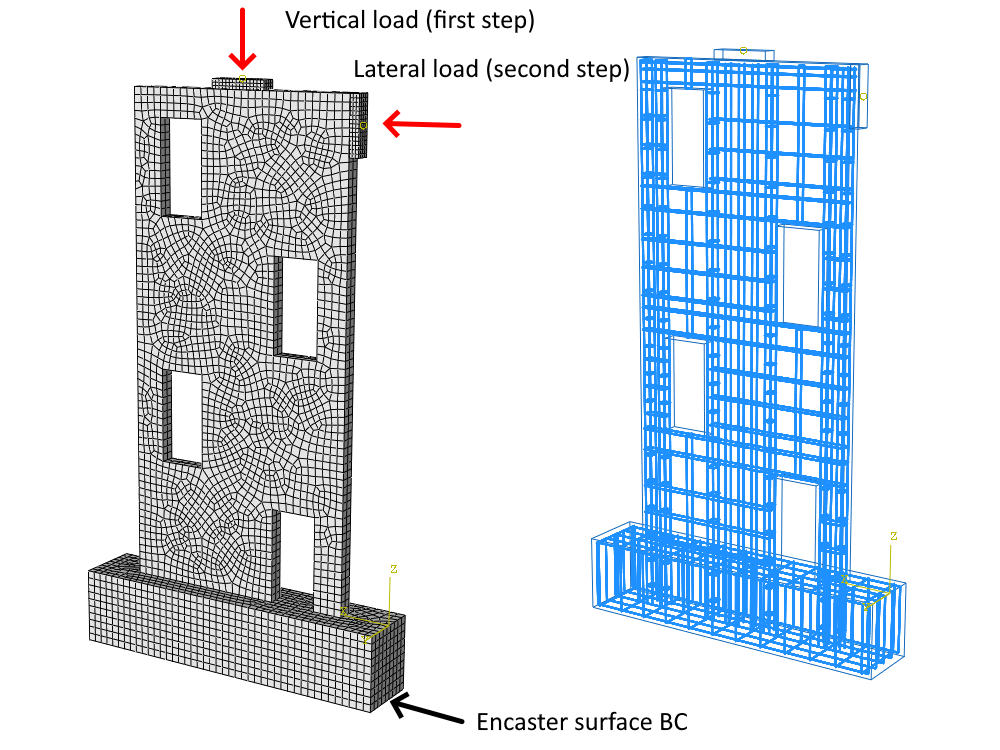
Il modello numerico è composto da elementi planari 2D in calcestruzzo e da barre di armatura 1D interconnesse tramite MPC ed elementi di collegamento alle parti in calcestruzzo. Il modello incorpora due dispositivi di supporto sotto forma di piastre in acciaio. La piastra superiore, di 350 x 80 x 20 mm, sostiene un carico verticale di 50 kN come fase iniziale del processo di carico. La seconda piastra, di 350 x 80 x 50 mm, è utilizzata come seconda fase per il carico laterale nel piano della parete, garantendo la distribuzione uniforme della forza concentrata durante il caricamento della parete. Il modello è incastrato, limitando i gradi di libertà Tx, Tz e Ry, e assume condizioni di sollecitazione piane 2D.

Fig. 4) Modello numerico in IDEA StatiCa Detail (processo di carico)

Modello di plasticità Drucker-Prager

Il modello numerico comprende elementi esaedrici 3D rinforzati con barre che sono rigidamente vincolate all'interno della regione di calcestruzzo ospitante. Il calcestruzzo e l'armatura di precompressione sono costituiti da elementi T3D2 che trasmettono esclusivamente gli effetti assiali. Lo scorrimento tra il calcestruzzo e le armature è completamente limitato da vincoli rigidi. Lo slittamento è simulato attraverso il rammollimento della tensione nel calcestruzzo, che porta alla cancellazione degli elementi al raggiungimento del 70% di danno nello stato post-critico. Questo approccio, in una certa misura, tiene conto del modello di coesione o dell'effetto tassello. Gli attributi del modello e delle piastre corrispondono esattamente alle ipotesi del CSFM.

Fig. 5) Modello numerico in ABAQUS (processo di carico)

Analisi

Il processo di carico comporta l'aumento incrementale delle deformazioni nelle direzioni laterali come parte del processo di carico monotono. Il carico ciclico non è stato preso in considerazione in questa analisi.

Gli approcci numerici variano leggermente tra le soluzioni dal punto di vista dell'analisi. Il CSFM impiega la teoria delle piccole deformazioni e incorpora l'analisi non lineare del materiale. Al contrario, il modello Drucker-Prager e ABAQUS impiega un'analisi geometrica e materiale non lineare, fornendo una soluzione più precisa quando si affrontano grandi deformazioni.

Sensibilità della mesh

L'analisi di sensibilità fornisce indicazioni sulle discrepanze derivanti dalla discretizzazione. La configurazione predefinita del CSFM prevede un moltiplicatore di maglia pari a uno, che aderisce alla regola di incorporare un minimo di quattro elementi sul bordo più piccolo del modello. Successivamente, l'intero modello viene meshato secondo questa regola. La stessa strategia è stata utilizzata per il modello in ABAQUS.

Metodo del campo di sollecitazione compatibile - Dettaglio IDEA StatiCa

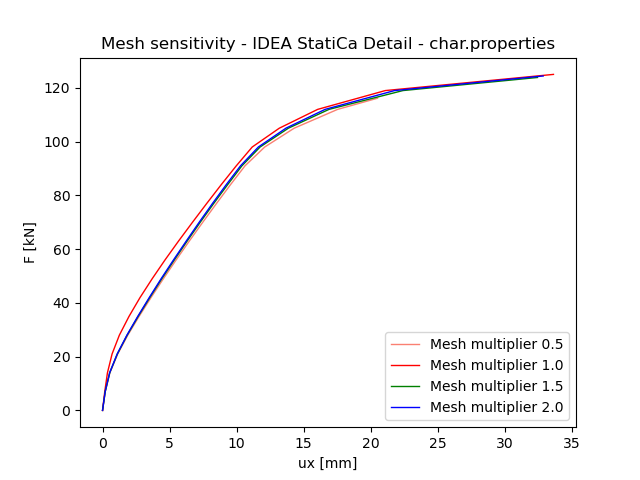
I dati dimostrano che l'errore medio tra i moltiplicatori di maglia di 0,5 e 2,0 è del 7%. Ciò ha portato a un approccio numerico a bassa sensibilità.

Fig. 6 Sensibilità della maglia IDEA StatiCa Detail

Modello di plasticità Drucker-Prager

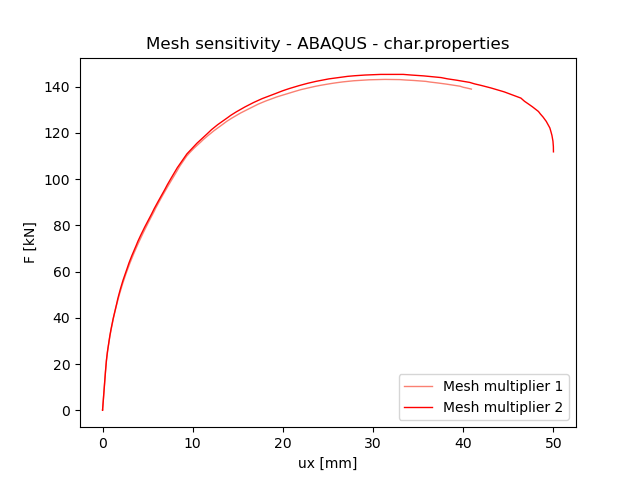
L'utilizzo di elementi esaedrici 3D produce una forza massima quasi identica quando si impiega un moltiplicatore di maglia di 1,0 e 2,0. La discrepanza nella forza massima consentita ammonta all'1,3%, suggerendo una soluzione insensibile alle maglie. Il modello considera un angolo di dilatazione di 30 gradi ai fini dell'analisi.

Fig. 7) Sensibilità della maglia ABAQUS

Risultati

Si noti quanto segue: I valori forniti, come la sollecitazione principale in compressione, le deformazioni, la sollecitazione massima in compressione e in trazione sulla barra di rinforzo e la posizione del danno, sono illustrati nelle figure successive. Tutti i valori sono presentati per un moltiplicatore di maglia di 1,0, utilizzato come parametro di verifica in CSFM[1] e successivamente applicato alla soluzione Drucker-Prager in ABAQUS[2]. L'angolo di dilatazione utilizzato sulla superficie di plasticità di Drucker-Prager è stato impostato a 30 gradi. I risultati saranno presentati per le proprietà caratteristiche e di progetto del materiale, valutate in base all'Eurocodice 1992-1[3].

Sollecitazioni principali in compressione

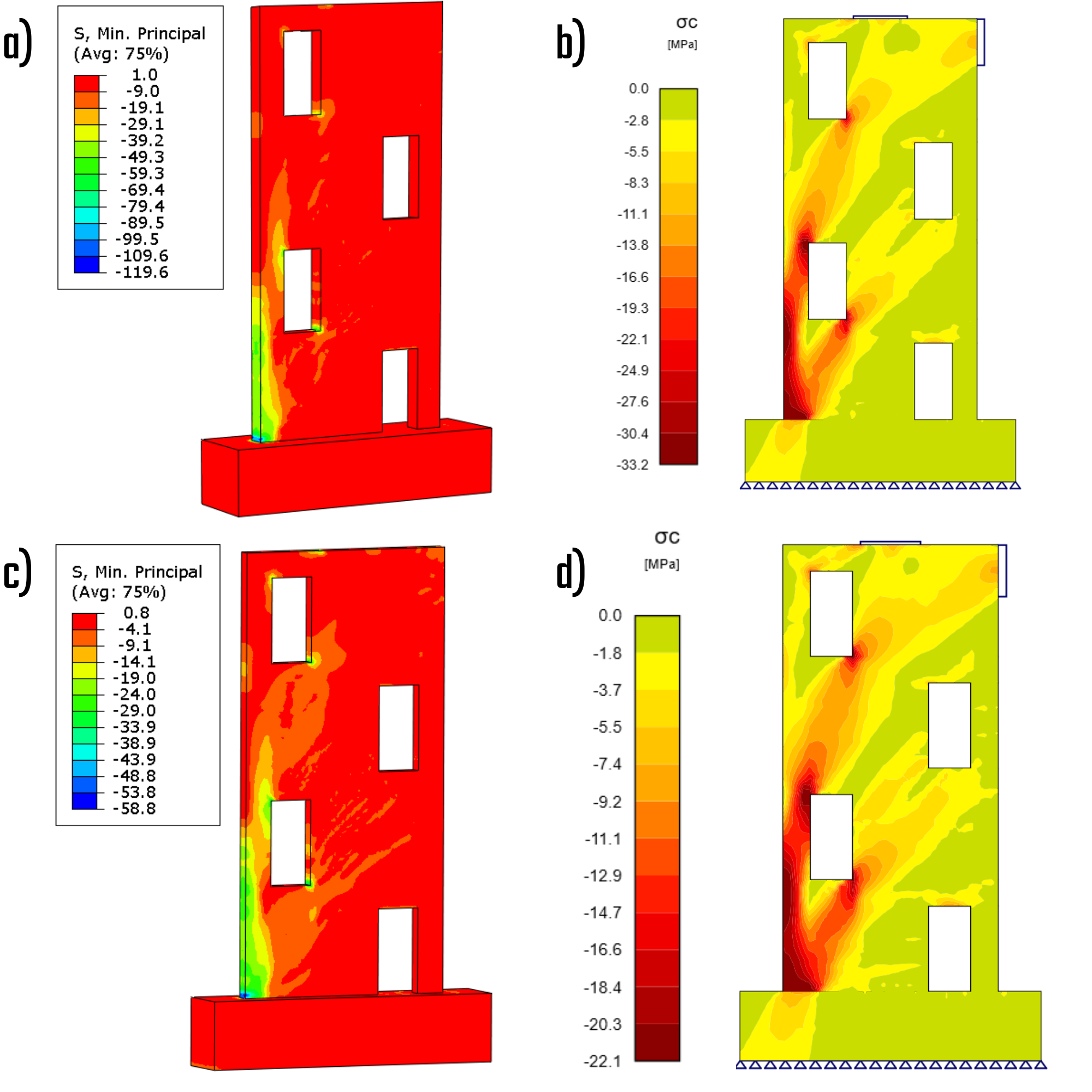
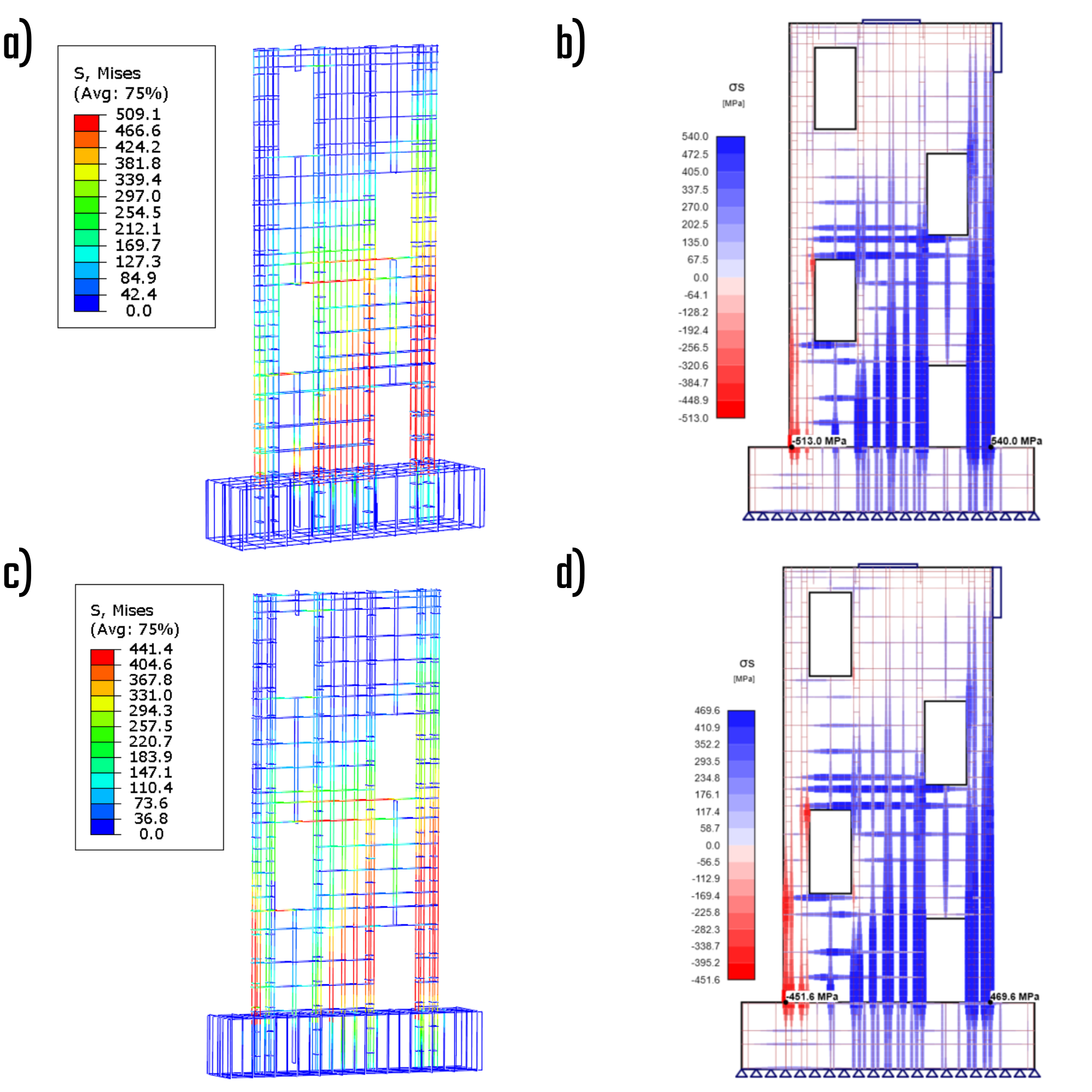
La principale distinzione tra la soluzione CSFM e la soluzione Drucker-Prager riguarda il trattamento delle sollecitazioni. La soluzione Drucker-Prager incorpora la pressione di confinamento, che ha la capacità di elevare in modo significativo la tensione principale minima in compressione, consentendo così al materiale di resistere a livelli di stress elevati. Al contrario, la soluzione CSFM determina la massima resistenza uniassiale caratteristica o di progetto del materiale, facilitando il confronto con le librerie di materiali standard. Le distribuzioni delle sollecitazioni tra le soluzioni presentano notevoli variazioni nelle regioni in cui l'effetto di confinamento è pronunciato.

Fig. 8) a) Sollecitazione principale in compressione - caratteristica (ABAQUS); b) Sollecitazione principale in compressione - caratteristica (IDEA StatiCa); c) Sollecitazione principale in compressione - progetto (ABAQUS); d) Sollecitazione principale in compressione - progetto (IDEA StatiCa)

Sollecitazioni nei rinforzi

Le sollecitazioni subite dalle barre di armatura offrono informazioni preziose sulla coerenza dei risultati e sulle aree specifiche in cui si concentrano le sollecitazioni elevate.

Fig. 9) a) Sollecitazioni nelle barre - caratteristica (ABAQUS); b) Sollecitazioni nelle barre - caratteristica (IDEA StatiCa); c) Sollecitazioni nelle barre - progetto (ABAQUS); d) Sollecitazioni nelle barre - progetto (IDEA StatiCa)

Deformazioni

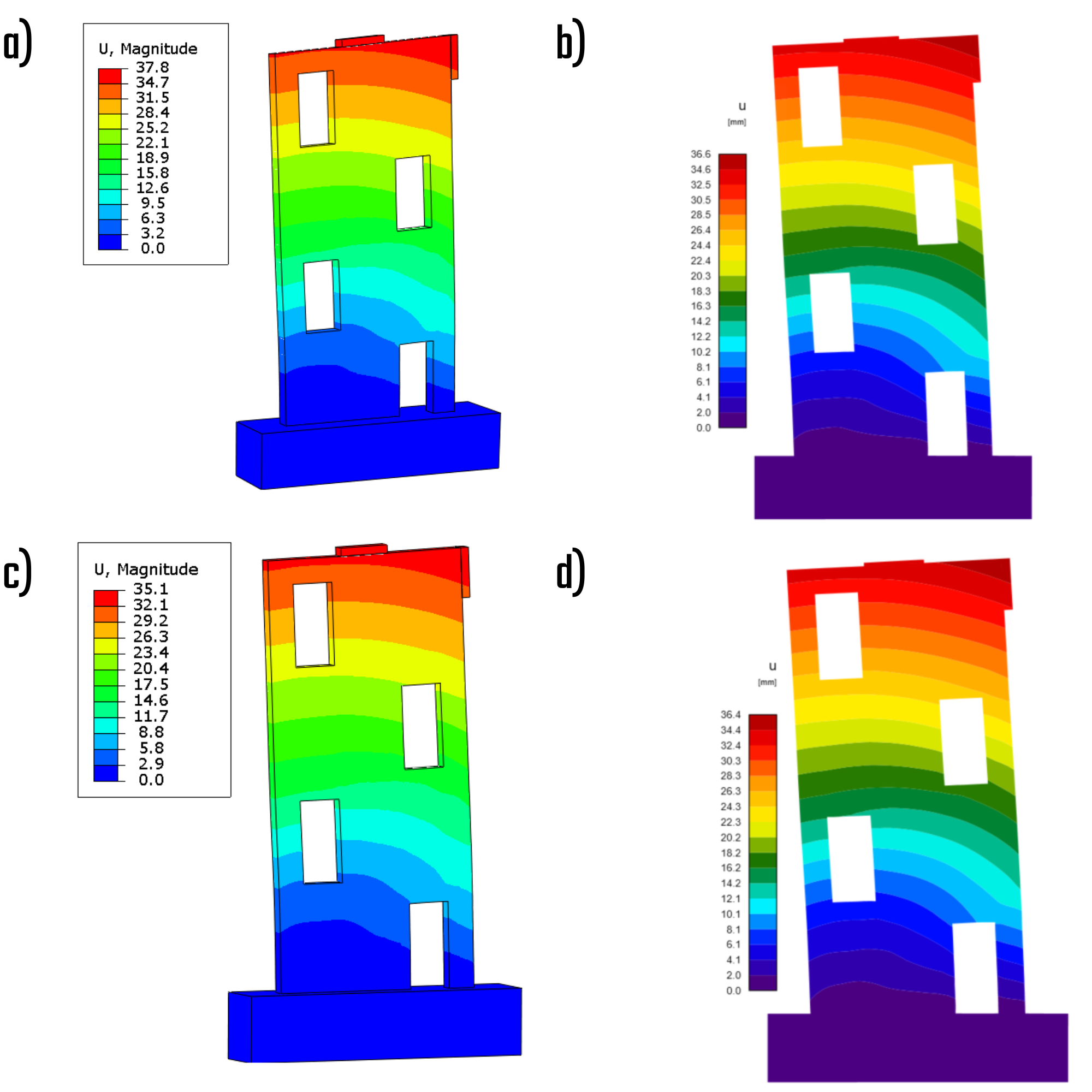
Le deformazioni servono a dimostrare che la non linearità geometrica ha implicazioni trascurabili, data la coerenza garantita dalla soluzione CSFM e dall'analisi non lineare dei materiali. Ciò suggerisce che, per lo specifico campione di parete in questione, l'effetto del secondo ordine non eserciterà alcuna influenza sul comportamento strutturale.

Fig. 10) a) Deformazioni totali - caratteristica (ABAQUS); b) Deformazioni totali - caratteristica (IDEA StatiCa); c) Deformazioni totali - progetto (ABAQUS); d) Deformazioni totali - progetto (IDEA StatiCa)

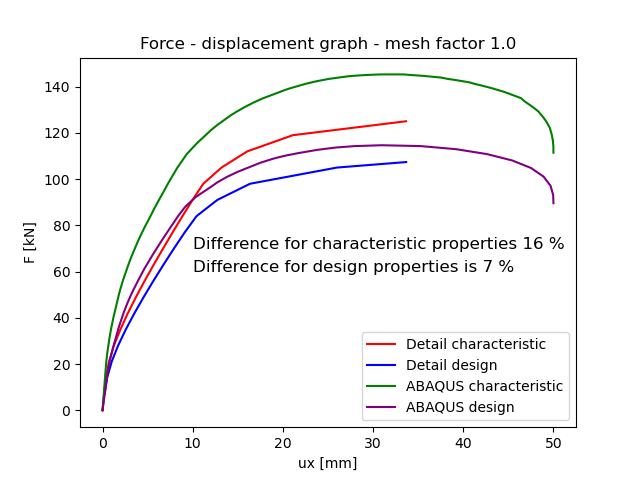
Grafico forze-deformazioni

La rappresentazione grafica chiarisce efficacemente l'intricata risposta della parete al carico laterale. La soluzione CSFM indica una riduzione della capacità portante di circa il 16% per le proprietà caratteristiche del materiale e del 7% per quelle di progetto. Queste differenze derivano dall'incorporazione del comportamento a trazione del calcestruzzo nel modello di plasticità di Drucker-Prager. Le deviazioni del 16% e del 7% osservate nella soluzione CSFM rientrano in un margine di sicurezza accettabile.

Fig. 11) Grafico della forza di deformazione

Conclusione

Lo studio sottolinea il ruolo critico delle pareti di taglio nel resistere ai carichi laterali di eventi dinamici come terremoti e tempeste di vento, garantendo così la stabilità e la sicurezza della struttura. Le pareti di taglio, posizionate strategicamente all'interno dei progetti degli edifici, aiutano a distribuire le forze laterali, in particolare nelle strutture di alto livello, essendo spesso collocate intorno ai vani degli ascensori e delle scale.

L'analisi ha utilizzato quattro modelli di verifica basati su valori caratteristici e di progetto secondo l'Eurocodice 1992-1-1, impiegando il Compatible Stress Field Method (CSFM)[1] e il Drucker-Prager Plasticity Model (DPPM)[2]. Lo studio ha coinvolto modelli in scala ridotta e specifiche geometriche e dei materiali dettagliate, con ipotesi adattate a ciascun metodo di analisi.

Il CSFM si è concentrato sulla massima sollecitazione principale del calcestruzzo e sulle sollecitazioni delle armature, trascurando la resistenza a trazione del calcestruzzo ad eccezione degli effetti di irrigidimento della tensione. Il DPPM, invece, ha considerato l'attrito interno, le resistenze a trazione e a compressione e il comportamento post-critico attraverso i parametri di danno. Sono stati creati modelli numerici per entrambi i metodi, con approcci diversi al carico e ai vincoli.

L'analisi della sensibilità delle maglie ha indicato una bassa sensibilità per entrambi i metodi, con lievi discrepanze osservate nelle distribuzioni delle sollecitazioni e nelle deformazioni. I risultati hanno evidenziato le differenze nella gestione delle sollecitazioni, in particolare con la pressione di confinamento nel DPPM, e hanno mostrato che la non linearità geometrica ha effetti trascurabili sulle deformazioni.

Nel complesso, i grafici forza-deformazione hanno dimostrato la risposta della parete ai carichi laterali, con le soluzioni CSFM che indicano deviazioni accettabili rispetto a DPPM, affermando la robustezza di entrambi gli approcci nel garantire l'integrità strutturale sotto le forze laterali.

Riferimenti

[1] IDEA StatiCa. (n.d.). Background teorico per il dettaglio IDEA StatiCa. Recuperato il 30 maggio 2024, da https://www.ideastatica.com/support-center/theoretical-background-for-idea-statica-detail.

[2] Manuale d'uso dell'analisi Abaqus. Manuale d'uso dell'analisi Abaqus [online] www: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html

[3] EN 1992-1-1 Eurocodice 2: Progettazione di strutture in calcestruzzo - Parte I: Regole generali e regole per gli edifici. Comitato Europeo di Standardizzazione, 2002.

[4] Massone, L. M.; et al. Interazione taglio-flessione per pareti strutturali, 2006. ResearchGate. https://www. researchgate.net/publication/284079633_Shear-flexure_interaction_for_structural_walls (visitato il 01 gennaio 2006).