Analisi di fatica secondo la norma EN 1993-1-9
Questo articolo mostra come utilizzare le sollecitazioni nominali fornite da IDEA Connection per eseguire l'analisi di fatica completa in conformità alla norma EN 1993-1-9.
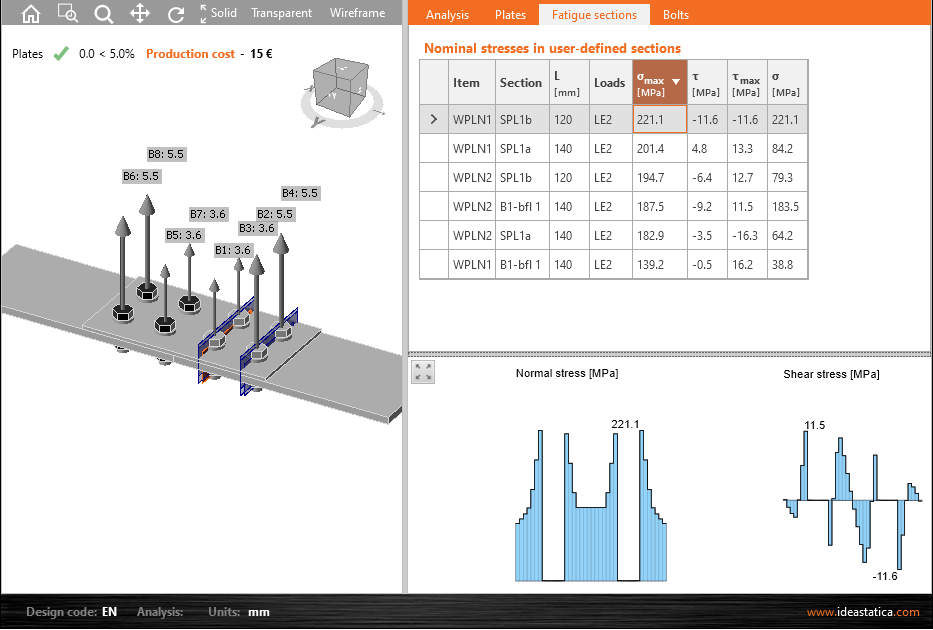
IDEA Connection fornisce le sollecitazioni nominali in:
- sezioni definite dall'utente
- sezioni in prossimità delle saldature
- bulloni e ancoraggi
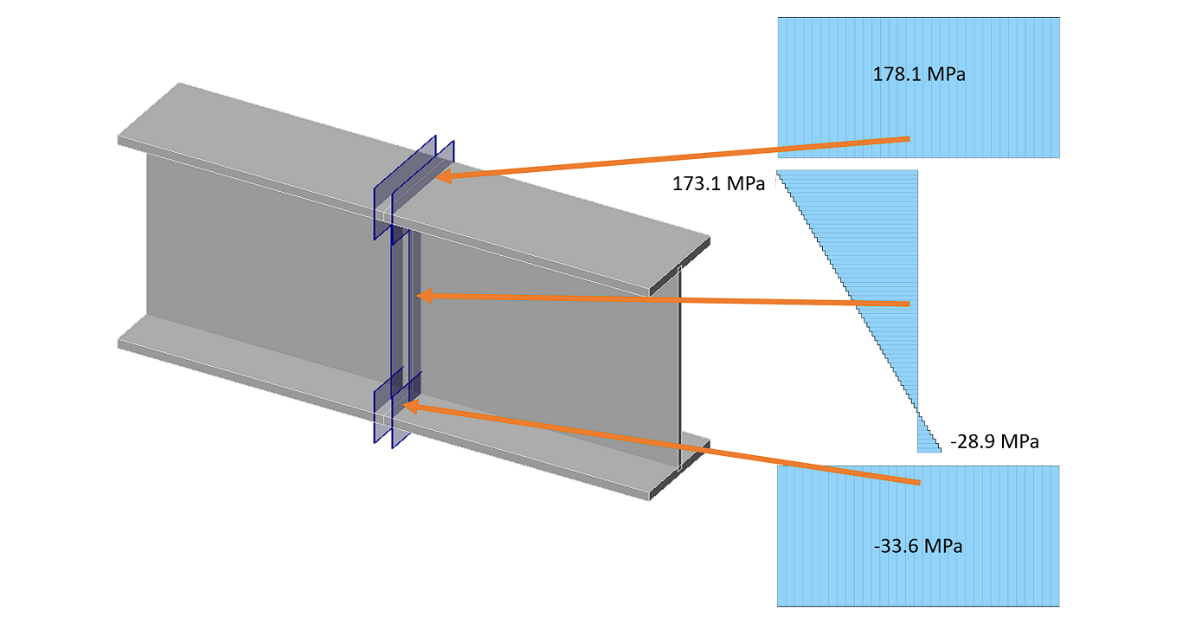
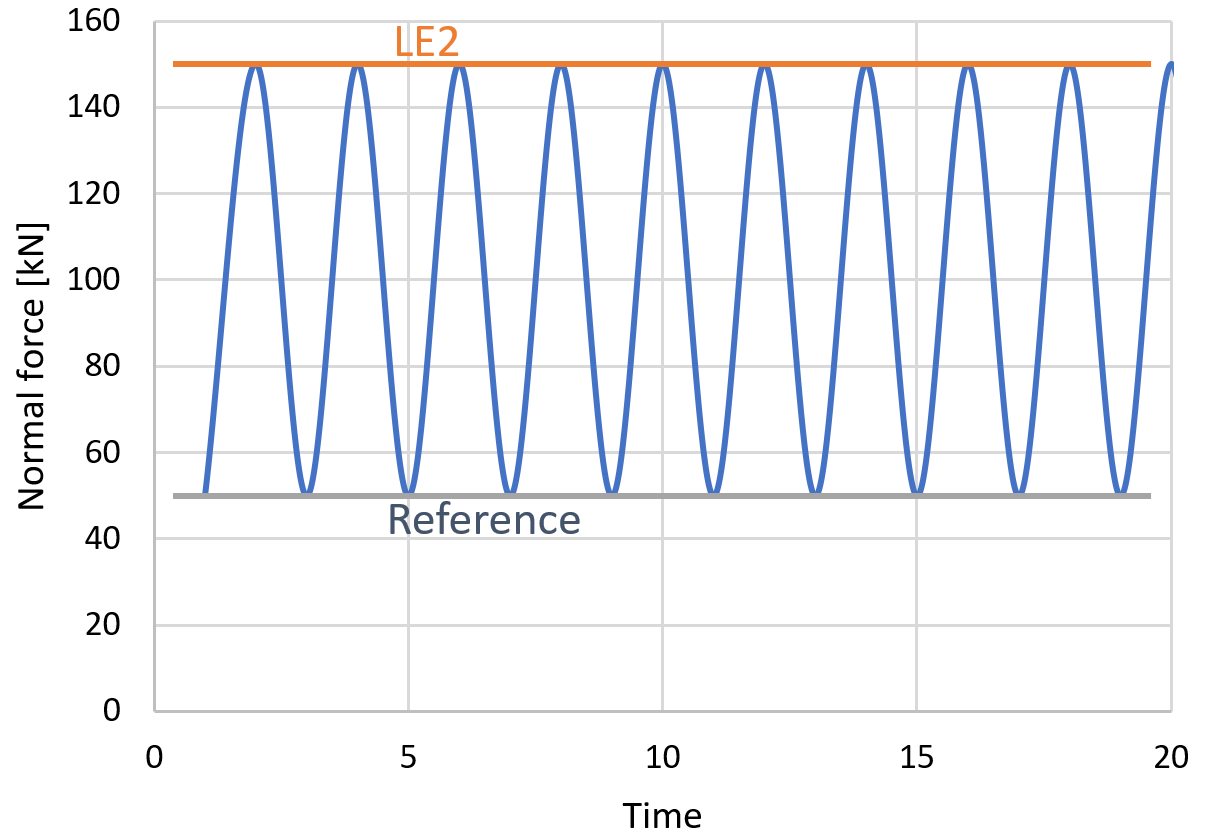
Le sollecitazioni fornite sono l'intervallo di sollecitazioni tra l'effetto del carico e l'effetto del carico di riferimento. L'intervallo di sollecitazioni non viene modificato in alcun modo, ad esempio in base alla figura seguente, che consente di diminuire l'intervallo di sollecitazioni se la sollecitazione passa dalla tensione alla compressione.
Queste sollecitazioni includono alcuni fattori di concentrazione delle sollecitazioni, ad esempio la concentrazione delle sollecitazioni in prossimità dei fori dei bulloni.
Devono essere inclusi altri fattori, ad esempio il fattore parziale per gli intervalli di sollecitazione equivalenti ad ampiezza costante \(\gamma_{Ff}\) secondo la norma EN 1991 o i fattori k1 per i giunti a sezione cava a causa dei momenti flettenti trascurati nel modello di capriata.
IDEA Connection fornisce \(\sigma_{max}\) e \(\tau_{max}\) da utilizzare per ottenere \(\Delta \sigma\) e \(\Delta \tau\).
\[ \Delta \sigma = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
\[ \Delta \tau = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
dove:
- \(\gamma_{Ff}\) - fattore parziale per campi di sollecitazione equivalenti ad ampiezza costante
- \(k_x\) - qualsiasi fattore non incluso nell'analisi, ad esempio \(k_1\) dalla Tabella 4.1 o 4.2
- \(\sigma_{max}\) - output IDEA Connection dello sforzo normale
- \(\tau_{max}\) - IDEA Uscita della connessione per lo sforzo di taglio
Secondo il Capitolo 8, Equazione (8.1), devono essere soddisfatti i seguenti limiti di sollecitazione:
\[\Delta \sigma \le 1,5 f_y\]
\[\Delta \tau \le 1,5 f_y / \sqrt{3}\]
dove \(f_y\) è la resistenza allo snervamento dell'acciaio.
Il dettaglio deve essere classificato secondo le Tabelle 8.1-8.10 e tutti i fattori rilevanti devono essere presi in considerazione, ad esempio il fattore per gli effetti dimensionali. La categoria del particolare (ridotta per esempio del fattore di effetto dimensionale) fornisce la resistenza alla fatica a 2 milioni di cicli, \(\Delta \sigma_c\) e \(\Delta \tau_c\). I valori di \(\Delta \sigma_c\) e \(\Delta \tau_c\) devono essere ridotti del fattore parziale per la resistenza alla fatica, \(\gamma_{Mf}\).
Tabella 3.1 dalla EN 1993-1-9 con i valori di \(\gamma_{Mf}\):
| Metodo di valutazione | Conseguenza del cedimento | |
| Conseguenza bassa | Conseguenze elevate | |
| Tolleranza al danno | 1 | 1.15 |
| Vita sicura | 1.15 | 1.35 |
I limiti della curva S-N (stress-life) sono determinati in base al capitolo 7.1:
Secondo il Capitolo A.5, si devono determinare i cicli fino al cedimento. Il numero di cicli, \(n_{Ei}\), associato all'intervallo di sollecitazioni \(\gamma_{Ff} \Delta \sigma_i\), è un input dell'utente. \(N_{Ri}\) è calcolato secondo il Capitolo 7.
Sollecitazioni normali per \(\Delta \sigma \ge \Delta \sigma_D\):
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m}\]
dove:
- m = 3 - pendenza della curva di resistenza a fatica
Sollecitazioni normali per \(\Delta \sigma \ge \Delta \sigma_L\):
\[N_R = \frac{\Delta \sigma_D^m \cdot 5\cdot 10^6}{\Delta \sigma^m} \]
dove:
- m = 5 - pendenza della curva di resistenza a fatica
Le sollecitazioni normali al di sotto del limite di taglio \(\Delta \sigma_L\) non partecipano al danno da fatica.
Le sollecitazioni di taglio per \(\Delta \tau_E \le \Delta \tau_L\):
\[N_R = \frac{\Delta \tau_c^m \cdot 2\cdot 10^6}{\Delta \tau^m} \]
dove:
- m = 5 - pendenza della curva di resistenza a fatica
Le sollecitazioni di taglio al di sotto del limite di cut-off \(\Delta \tau_L\) non partecipano al danno da fatica.
Il danno è calcolato secondo la regola di Palmgren-Miner (Figura A.1) nelle equazioni (A.1) e (A.2) separatamente per le sollecitazioni normali e di taglio:
\[D_d = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} \le 1.0\]
Lo sforzo normale e lo sforzo di taglio devono essere combinati mediante l'equazione (8.3), a meno che non sia indicato diversamente nelle tabelle 8.8 e 8.9.
\[D_{d \sigma}^3 + D_{d \tau}^5 \le 1,0 \]
Esempio
Ingressi per il calcolo: L'utente imposta un effetto di carico di riferimento e tre effetti di carico di fatica. I risultati di IDEA Connection sono la massima sollecitazione normale e la corrispondente sollecitazione di taglio. Il tipo di acciaio è S355.
| Effetto di carico | Numero di cicli | Sollecitazione normale massima | Sollecitazione di taglio corrispondente |
| nE | Δσmax [MPa] | Δτ [MPa] | |
| LE2 | 1 500 000 | 60 | 60 |
| LE3 | 3 000 000 | 50 | 40 |
| LE4 | 10 000 000 | 20 | 10 |
I fattori di sicurezza parziali sono determinati in base alle norme EN 1991 e EN 1993-1-9:
\[ \gamma_{Ff} = 1,0 \]
\[ \gamma_{Mf} = 1,15 \]
I limiti di sollecitazione sono controllati:
\[\Delta \sigma \le 1.5 f_y\]
\[ 60 \, \textrm{MPa} \le 1.5 \cdot 355 = 532 \, \textrm{MPa}\]
\[\Delta \tau \le 1,5 f_y / \sqrt{3} \]
\[60 \, \textrm{MPa} \le 1,5 \cdot 355 / \sqrt{3} = 307 \, \textrm{MPa} \]
Dalle tabelle 8.1-8.10, si determinano i valori di \(\Delta \sigma_c = 90\,\textrm{MPa}\) e \(\Delta \tau_c = 70\,\textrm{MPa}\). Questi valori sono ridotti di un fattore parziale per la resistenza alla fatica, \(\gamma_{Mf} = 1,15\) a \(\Delta \sigma_c = 78,3\,\textrm{MPa}\) e \(\Delta \tau_c = 60,9\,\textrm{MPa}\).
Vengono determinati i limiti della curva S-N:
\[\Delta \sigma_D = \left ( \frac{2}{5} \right )^{1/3} \Delta \sigma_c = \left ( \frac{2}{5} \right )^{1/3} 78.3 = 57.7\,\textrm{MPa}\]
\[\Delta \sigma_L = \left ( \frac{5}{100} \right )^{1/5} \Delta \sigma_D = \left ( \frac{5}{100} \right )^{1/5} 57.7 = 31.7 \,\textrm{MPa}\]
\[\Delta \tau_L = \left ( \frac{2}{100} \right )^{1/5} \Delta \tau_c = \left ( \frac{2}{100} \right )^{1/5} 60.9 = 27.8\,\textrm{MPa} \]
\(\Delta \sigma\) è determinato moltiplicando \(\Delta \sigma_{max}\) per il fattore parziale per campi di sollecitazione equivalenti ad ampiezza costante \(\gamma_{Ff} = 1,0\). In questo esempio, non è necessario alcun altro fattore kx.
Il numero di cicli fino alla rottura, \(N_R\), viene calcolato per ogni caso di carico e sollecitazione normale e di taglio secondo le formule sopra citate, ad esempio per la sollecitazione normale in LE2:
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m} = \frac{78.3^3 \cdot 2\cdot 10^6}{60^3} = 4 \,438\, 234 \, \textrm{cycles}\]
| Effetto del carico | Numero di cicli | Sollecitazione normale massima | Sollecitazione di taglio corrispondente | Numero di cicli fino alla rottura | Numero di cicli fino alla rottura | ||
| nE | Δσmax [MPa] | Δτ [MPa] | Δσ [MPa] | NR | Δτ [MPa] | NR | |
| LE2 | 1 500 000 | 60 | 60 | 60 | 4 438 235 | 60 | 2 149 190 |
| LE3 | 3 000 000 | 50 | 40 | 50 | 10 200 230 | 40 | 16 320 409 |
| LE4 | 10 000 000 | 20 | 10 | 20 | infinito | 10 | infinito |
Utilizzando la regola di Palmgren-Miner, si calcola il danno accumulato per tutti gli effetti del carico.
Per le sollecitazioni normali:
\[D_{d \sigma} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{4\, 438\, 235} + \frac{3\,000\,000}{10\,200\,230} = 0,632 \le 1,0\]
Per le sollecitazioni di taglio:
\[D_{d \tau} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{2\, 149\, 190} + \frac{3\,000\,000}{16\,320\,409} = 0,882 \le 1,0\]
Infine, si verifica l'interazione tra sforzo normale e di taglio:
\[ D_{d \sigma} ^3 + D_{d \tau} ^5 \le 1.0\]
\[ 0.632 ^3 + 0.882 ^5 = 0.786 \le 1.0\]
La resistenza alla fatica del particolare in esame è sufficiente.
Verifiche
Prima di rilasciare lo strumento di analisi della fatica, sono state eseguite diverse verifiche sperimentali:
Vita a fatica con il metodo delle tensioni nominali
Analisi di fatica - Saldature di testa di sezione I