Ermüdungsanalyse nach EN 1993-1-9
Dieser Artikel zeigt, wie die von IDEA Connection ausgegebenen Nennspannungen verwendet werden, um eine vollständige Ermüdungsanalyse gemäß EN 1993-1-9 durchzuführen.
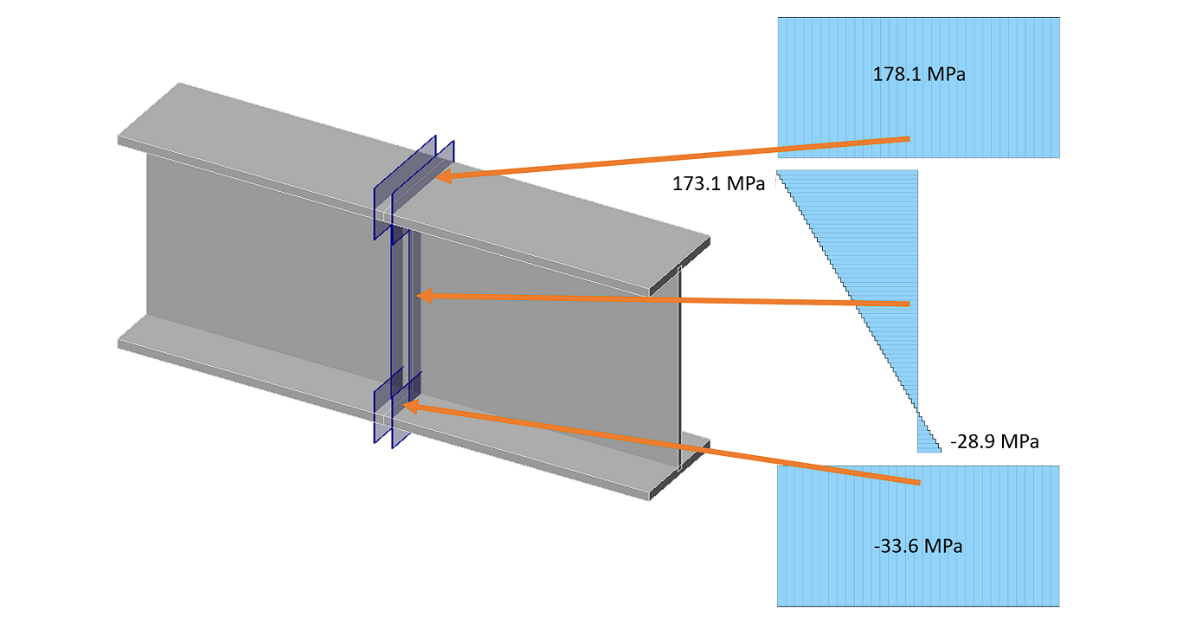
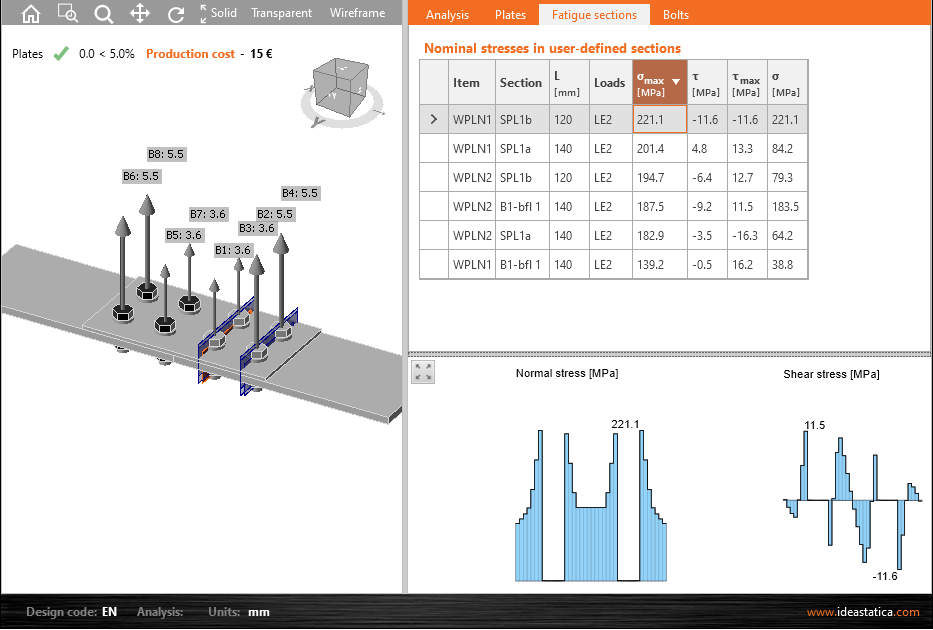
IDEA Connection gibt Nennspannungen in
- benutzerdefinierten Abschnitten
- Abschnitten nahe Schweißnähten
- Schrauben und Ankern
aus.
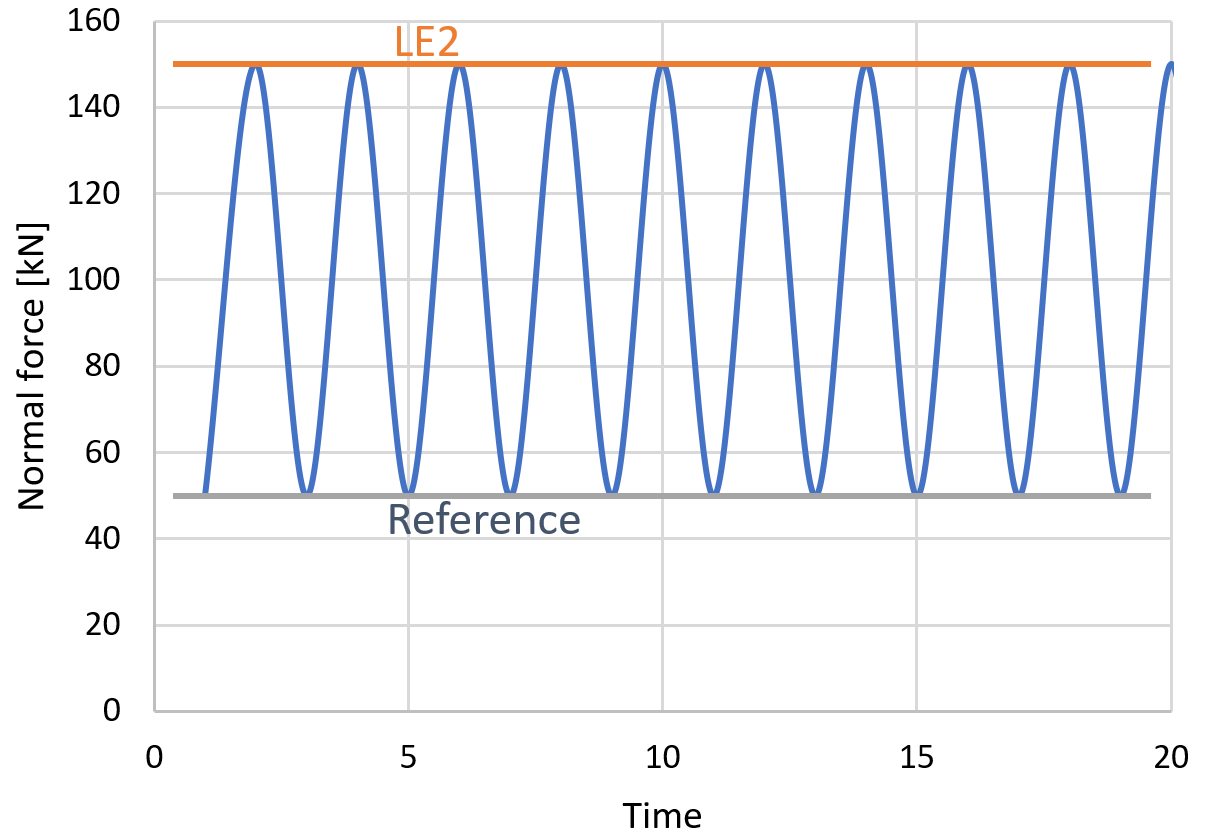
Die Spannungsausgabe ist der Spannungsbereich zwischen der Last und der Bezugslast. Der Spannungsbereich wird in keiner Weise verändert, z.B. in Bezug auf die unten gezeigte Abbildung, die eine Verringerung des Spannungsbereichs ermöglicht, wenn sich die Spannung von Zug zu Druck ändert.
Diese Spannugnen umfassen einige Faktoren zur Spannungskonzentration, z.B. Spannungskonzentration in der Nähe von Schraubenlöchern.
Andere Faktoren, z.B. Teilbeiwerte für äquivalente Spannungsschwingbreiten mit konstanter Amplitude \(\gamma_{Ff}\) nach EN 1991 oder k1-Beiwerte für Hohlprofilverbindungen aufgrund vernachlässigter Biegemomente im Fachwerkmodell müssen noch berücksichtigt werden.
IDEA Connection gibt \(\sigma_{max}\) und \(\tau_{max}\) aus, um \(\Delta\sigma\) und \(\Delta\tau\) zu erhalten.
\[ \Delta \sigma = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
\[ \Delta \tau = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
Wo:
- \(\gamma_{Ff}\) – Teilfaktor für äquivalente Spannungsschwingbreiten mit konstanter Amplitude
- \(k_x\) – Alle Faktoren, die nicht in der Analyse enthalten sind, z.B. \(k_1\) aus Tabelle 4.1 oder 4.2
- \(\sigma_{max}\) – IDEA Connection Ausgabe der Nennspannung
- \(\tau_{max}\) – IDEA Connection Ausgabe der Scherspannung
Nach Kapitel 8, Gleichung (8.1) müssen folgende Spannungsgrenzen eingehalten werden:
\[\Delta \sigma \le 1.5 f_y\]
\[\Delta \tau \le 1.5 f_y / \sqrt{3}\]
mit \(f_y\) als Streckgrenze des Stahls.
Das Detail ist nach den Tabellen 8.1–8.10 zu kategorisieren und alle relevanten Faktoren zu berücksichtigen, z.B. der Faktor für Größeneffekte. Die Detailkategorie (reduziert z.B. um den Faktor des Größeneffekts) liefert die Dauerfestigkeit bei 2 Millionen Zyklen, \(\Delta \sigma_c\) und \(\Delta \tau_c\). Die Werte von \(\Delta\sigma_c\) und \(\Delta\tau_c\) sollten um den Teilfaktor für die Ermüdungsfestigkeit \(\gamma_{Mf}\) reduziert werden.
Tabelle 3.1 aus EN 1993-1-9 mit den Werten von \(\gamma_{Mf}\):
| Bewertungsmethode | Folge des Versagens | |
| Geringe Folgen | Starke Folgen | |
| Schadenstoleranz | 1 | 1,15 |
| Lebensdauer | 1,15 | 1,35 |
Die Grenzen der S-N Kurve (Stress-Life) werden nach Kapitel 7.1 ermittelt:
\[\Delta \sigma_D = \left ( \frac{2}{5} \right )^{1/3} \Delta \sigma_c \]
\[\Delta \sigma_L = \left ( \frac{5}{100} \right )^{1/5} \Delta \sigma_D \]
\[\Delta \tau_L = \left ( \frac{2}{100} \right )^{1/5} \Delta \tau_c \]
Gemäß Kapitel A.5 sind Zyklen bis zum Versagen zu bestimmen. Die Anzahl der Zyklen, \(n_{Ei}\), verbunden mit dem Spannungsbereich \(\gamma_{Ff} \Delta \sigma_i\), sind Benutzereingaben. \(N_{Ri}\) wird nach Kapitel 7 berechnet.
Normalspannungen für \(\Delta \sigma \ge \Delta \sigma_D\):
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m}\]
wo:
- m = 3 – Steigung der Ermüdungsfestigkeitskurve
Normalspannungen für \(\Delta \sigma \ge \Delta \sigma_L\):
\[N_R = \frac{\Delta \sigma_D^m \cdot 5\cdot 10^6}{\Delta \sigma^m} \]
wo:
- m = 5 – Steigung der Ermüdungsfestigkeitskurve
Die Normalspannungen unterhalb der Abschaltgrenze \(\Delta \sigma_L\) haben keinen Anteil an Ermüdungsschäden.
Schubspannungen für \(\Delta \tau_E \le \Delta \tau_L\):
\[N_R = \frac{\Delta \tau_c^m \cdot 2\cdot 10^6}{\Delta \tau^m} \]
wo:
- m = 5 – Steigung der Ermüdungsfestigkeitskurve
Die Normalspannungen unterhalb der Abschaltgrenze \(\Delta \tau_L\) haben keinen Anteil an Ermüdungsschäden.
Der Schaden wird nach der Palmgren-Miner-Regel (Bild A.1) in den Gleichungen (A.1) und (A.2) getrennt für Normal- und Schubspannung berechnet:
\[D_d = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} \le 1.0\]
Normalspannung und Schubspannung sind nach Gleichung (8.3) zu kombinieren, sofern in den Tabellen 8.8 und 8.9 nichts anderes angegeben ist.
\[D_{d\sigma}^3 + D_{d\tau}^5 \le 1.0 \]
Beispiel
Eingaben für die Berechnung: Der Benutzer stellt eine Bezugslast und drei Ermüdungslastwirkungen ein. Die Ausgaben von IDEA Connection sind die maximale Normalspannung und die entsprechende Schubspannung. Die Stahlklasse ist S355.
| Lasten | Anzahl der Zyklen | Maximale Normalbelastung | Entsprechende Schubspannung |
| nE | Δσmax [MPa] | Δτ [MPa] | |
| LE2 | 1 500 000 | 60 | 60 |
| LE3 | 3 000 000 | 50 | 40 |
| LE4 | 10 000 000 | 20 | 10 |
Teilsicherheitsbeiwerte werden aus EN 1991 und EN 1993-1-9 ermittelt:
\[ \gamma_{Ff} = 1.0 \]
\[ \gamma_{Mf} = 1.15 \]
Spannungsgrenzen werden geprüft:
\[\Delta \sigma \le 1,5 f_y\]
\[ 60 \, \textrm{MPa} \le 1,5 \cdot 355 = 532 \, \textrm{MPa}\]
\[\Delta \tau \le 1.5 f_y / \sqrt{3} \]
\[60 \, \textrm{MPa} \le 1,5 \cdot 355 / \sqrt{3} = 307 \, \textrm{MPa} \]
Aus den Tabellen 8.1–8.10 werden Werte von \(\Updelta \sigma_c = 90\,\textrm{MPa}\) und \(\Updelta \tau_c = 70\,\textrm{MPa}\) ermittelt. Diese Werte werden um den reduzierten Teilfaktor für die Dauerfestigkeit, \(\gamma_{Mf} = 1,15\) auf \(\Updelta \sigma_c = 78,3\,\textrm{MPa}\) und \(\Updelta \tau_c = 60,9\,\textrm{MPa}\).
Die Grenzen der S-N Kurve sind festgelegt
\[\Delta \sigma_D = \left ( \frac{2}{5} \right )^{1/3} \Delta \sigma_c = \left ( \frac{2}{5} \right )^{1/3} 78,3 = 57,7\,\textrm{MPa}\]
\[\Delta \sigma_L = \left ( \frac{5}{100} \right )^{1/5} \Delta \sigma_D = \left ( \frac{5}{100} \right )^{1/5} 57,7 = 31,7 \,\textrm{MPa}\]
\[\Delta \tau_L = \left ( \frac{2}{100} \right )^{1/5} \Delta \tau_c = \left ( \frac{2}{100} \right )^{1/5} 60,9 = 27,8\,\textrm{MPa} \]
\(\Updelta \sigma\) wird durch Multiplizieren von \(\Updelta \sigma_{max}\) mit dem Teilfaktor für äquivalente Spannungsbereiche mit konstanter Amplitude \(\gamma_{Ff} = 1,0\) bestimmt. In diesem Beispiel ist kein weiterer Faktor kx erforderlich.
Die Anzahl der Zyklen bis zum Versagen, \(N_R\) wird für jeden Lastfall und Normal- und Schubspannung nach den oben genannten Formeln berechnet, z.B. für Normalspannung in LE2:
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m} = \frac{78.3^3 \cdot 2\cdot 10^6}{60^3} = 4 \,438\, 234 \, \textrm{cycles}\]
| Lasten | Anzahl der Zyklen | Maximale Normalbe-lastung | Entsprechende Schub-spannung | Anzahl der Zyklen bis zum Ausfall | Anzahl der Zyklen bis zum Ausfall | ||
| nE | Δσmax [MPa] | Δτ [MPa] | Δσ [MPa] | NR | Δτ [MPa] | NR | |
| LE2 | 1 500 000 | 60 | 60 | 60 | 4 438 235 | 60 | 2 149 190 |
| LE3 | 3 000 000 | 50 | 40 | 50 | 10 200 230 | 40 | 16 320 409 |
| LE4 | 10 000 000 | 20 | 10 | 20 | unendlich | 10 | unendlich |
Nach der Palmgren-Miner-Regel wird der kumulierte Schaden für alle Lasten berechnet.
Bei normalen Belastungen:
\[D_{d \sigma} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{4\, 438\, 235} + \frac{3\,000\,000}{10\,200\,230} = 0,632 \le 1,0\]
Für Schubspannungen:
\[D_{d \tau} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{2\, 149\, 190} + \frac{3\,000\,000}{16\,320\,409} = 0,882 \le 1,0\]
Abschließend wird die Interaktion von Normal- und Schubspannung überprüft:
\[ D_{d \sigma} ^3 + D_{d \tau} ^5 \le 1,0\]
\[ 0,632 ^3 + 0,882 ^5 = 0.786 \le 1,0\]
Die Ermüdungsfestigkeit des untersuchten Details ist ausreichend.
Überprüfungen
Vor der Freigabe des Ermüdungsanalysewerkzeugs wurden mehrere experimentelle Überprüfungen durchgeführt:
Fatigue life by nominal stress method
Fatigue analysis – Butt welds of I section