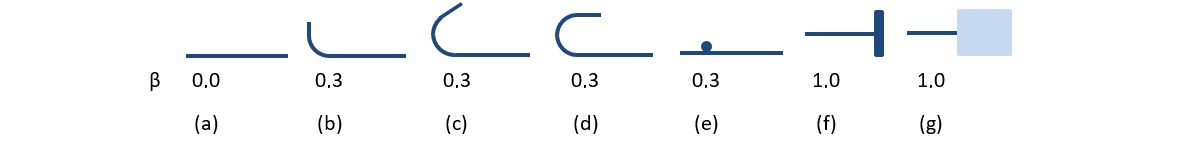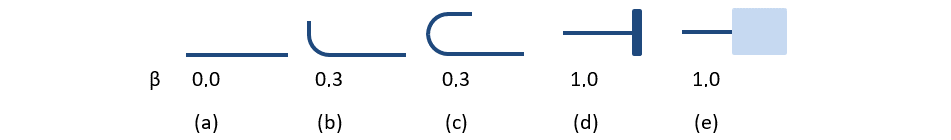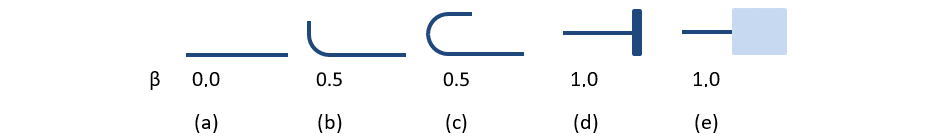In practice, engineers may encounter different types of finite elements (from simple 1D bar elements to more complicated 3D brick elements) that are used in a variety of applications for the analysis and design of structural elements. A common feature of most of the computations in practice tends to be the linear behavior of the models, the advantages of which are undoubtedly speed, clarity, and simply the fact that for a large variety of problems, this solution is quite sufficient.

Especially in the world of concrete structures, it often happens that the linear approach is not sufficient simply because after the first cracks appear in the loaded element, the stresses are redistributed and the problem becomes significantly non-linear.

For these cases, it is necessary to choose one of the more sophisticated approaches. For 1D cases, analytical methods defined directly in codes can often be found. For example, popular Strut and Tie models can be built for 2D planar elements and discontinuity regions (D-regions), or the more sophisticated stress field method implemented in IDEA StatiCa Detail, CSFM, can be used.

However, if the engineer encounters a problem that cannot be simplified into planar behavior, the options are very limited. Of course, a 3D Strut and Tie model can be built or semi-scientific software can be used for accurate analysis. These procedures are often time-consuming, not code-compliant, and require an engineer knowledgeable in advanced modeling methods.

For this reason, IDEA StatiCa has developed and implemented the 3D CSFM (Compatible Stress Field Method) in the Detail application. 3D CSFM extends the established CSFM into a third dimension, offering a fast and code-compliant solution that is primarily applicable to the everyday engineer, giving them a unique new ability to safely tackle the complex details of concrete structures.

Main assumptions and limitations

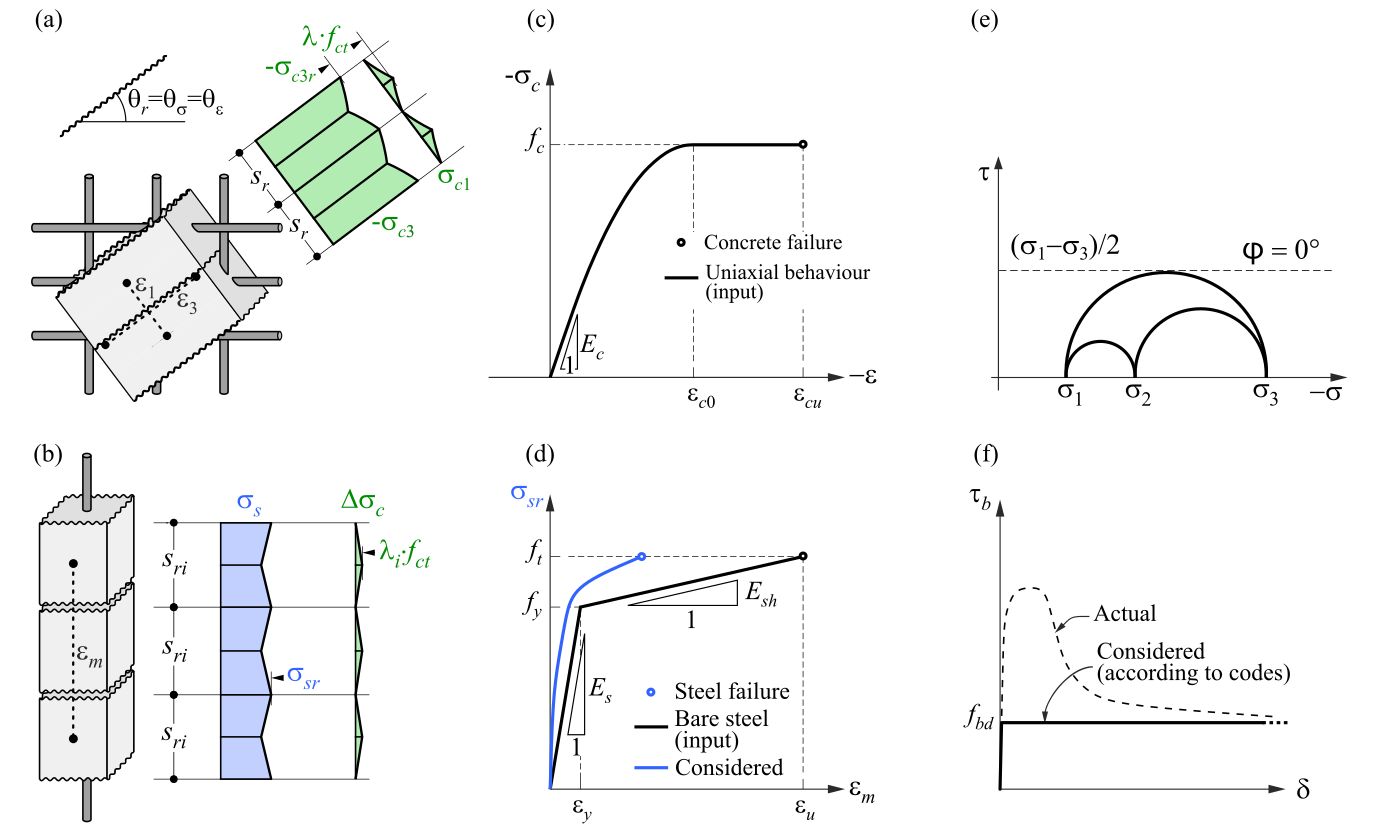
3D CSFM defines the concrete behavior based on the Modified Mohr-Coulomb plasticity theory for monotonic loading. The method considers principal concrete stresses in compression and reinforcement stresses (σ_sr) at the cracks while neglecting the concrete tensile strength (tension cut-off), except for its stiffening effect on the reinforcement (Tension stiffening).

σ_c₁_r, σ_c₂_r, σ_c₃_r ≤ 0 MPa

The reinforcement bars are linked to concrete volume finite elements through bond elements, allowing for slip between the concrete and reinforcement. It should be noted that 3D CSFM is not suitable for simulating plain concrete due to the absence of tension, which may result in misleading deformation and model divergence. Generally, the Mohr-Coulomb theory includes two fundamental properties governing the evolution of the plasticity surface in compression and partially in tension: the internal friction angle φ and cohesion parameter c. 3D CSFM assumes a zero angle of internal friction (Fig. 1e), leading to a conservative design due to the plasticity surface resembling the Tresca model, which is independent of the first stress invariant.

\( \textsf{\textit{\footnotesize{Fig. 1\qquad Basic assumptions of the 3D CSFM: (a) principal stresses in concrete; (b) stresses in the reinforcement direction;}}}\) \( \textsf{\textit{\footnotesize{(c) stress-strain diagram of concrete in terms of maximum stresses; (d) stress-strain diagram of reinforcement}}}\) \( \textsf{\textit{\footnotesize{in terms of stresses at cracks and average strains; (e) Mohr's circles for concrete model in 3D CSFM; (f) bond shear stress-slip}}}\) \( \textsf{\textit{\footnotesize{relationship for anchorage length verifications.}}}\)

Concrete

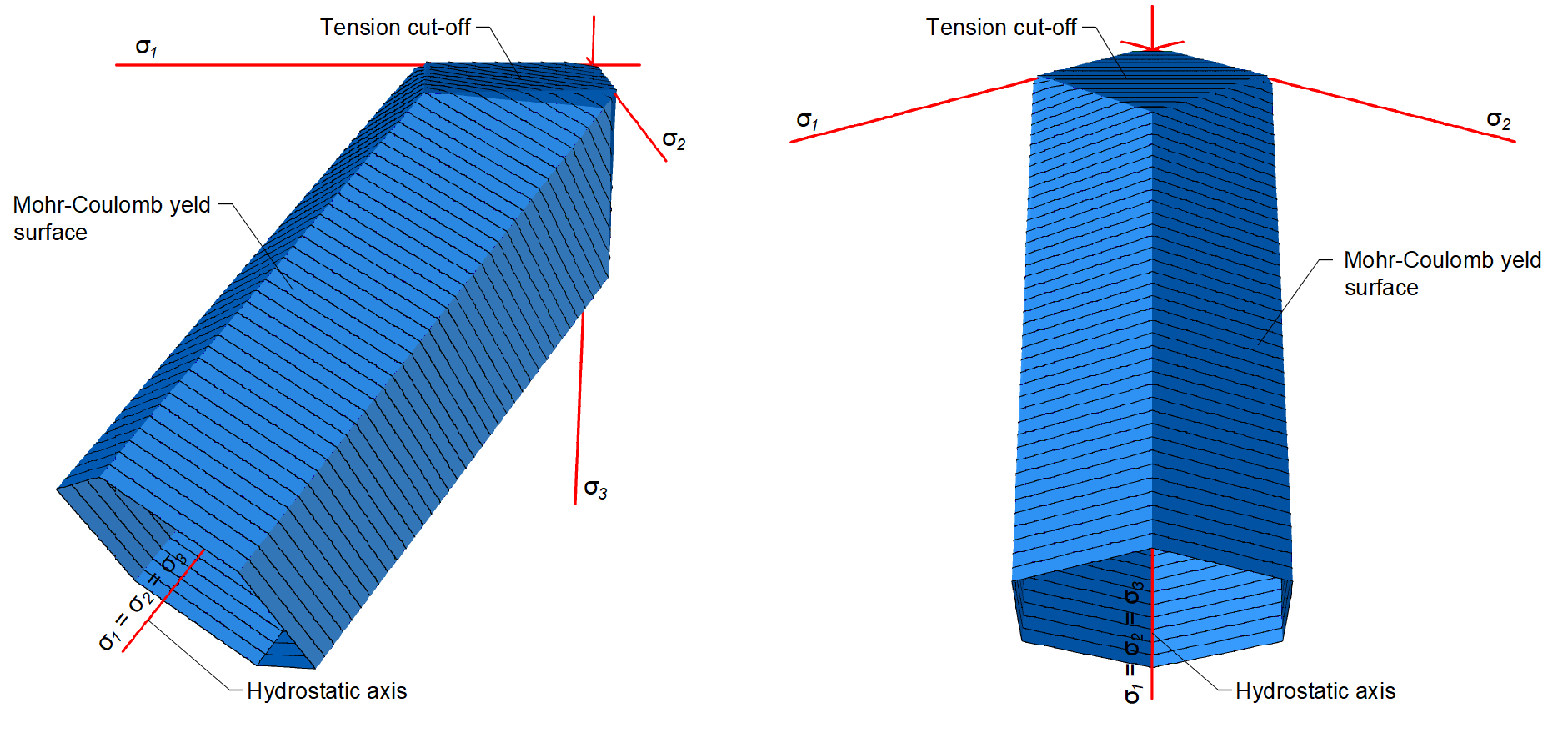
The presented material model is a multisurface plasticity model given by the combination of the Mohr-Coulomb and Rankine models for monotonic loading. It’s important to note that this model does not address unloading, therefore, state variables are not stored, as they would be in classical plasticity models used for cyclic loading.

\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Mohr-Coulomb multi-surface plasticity model for friction angle 0 degree}}}\]

As already mentioned, the material model is intended for use in applications that calculate the response of reinforced concrete (not suitable for plain concrete). This is due to the exclusion of concrete in tension. Therefore, the model is not even suitable for structural elements where the design rules for reinforced concrete such as minimum reinforcement ratio, maximum bar spacing, etc., are not fulfilled. It should also be added that, for numerical stability reasons, a very small tensile capacity is defined in the model. The tensile part is restricted by planes corresponding to the Rankine model.

3D CSFM in IDEA StatiCa Detail does not consider an explicit failure criterion in terms of strains for concrete in compression (i.e., it considers an infinitely plastic branch after the peak stress is reached). This simplification does not allow the deformation capacity of structures failing in compression to be verified. However, their ultimate capacity is properly predicted when the increase in the brittleness of concrete as its strength rises is considered by means of the 𝜂_𝑓𝑐 reduction factor defined in fib Model Code 2010 as follows:

\[f_{c,red} = \eta _{fc} \cdot f_{c}\]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]

where:

f_c is the concrete cylinder characteristic strength (in MPa for the definition of \( \eta_{fc} \)).

The f_c,red is then compared with the Equivalent Principal Stress σ_c,eq in concrete, which will be defined further, of course, with consideration of all safety factors prescribed by code.

A detailed description of the concrete model can be found at the following link:

Concrete Material Model for 3D Detail

Reinforcement

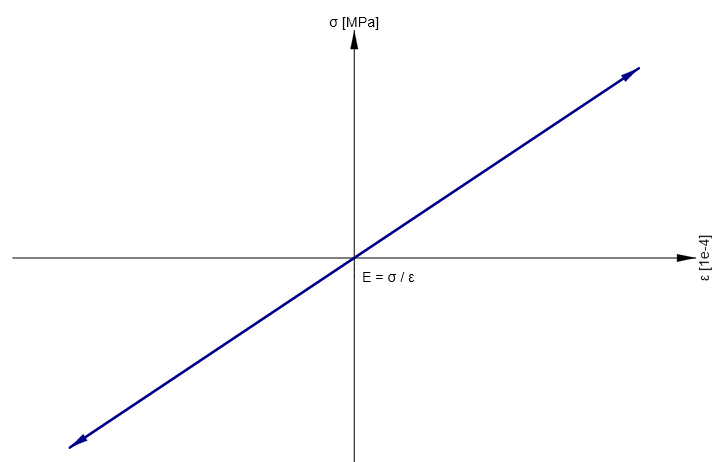
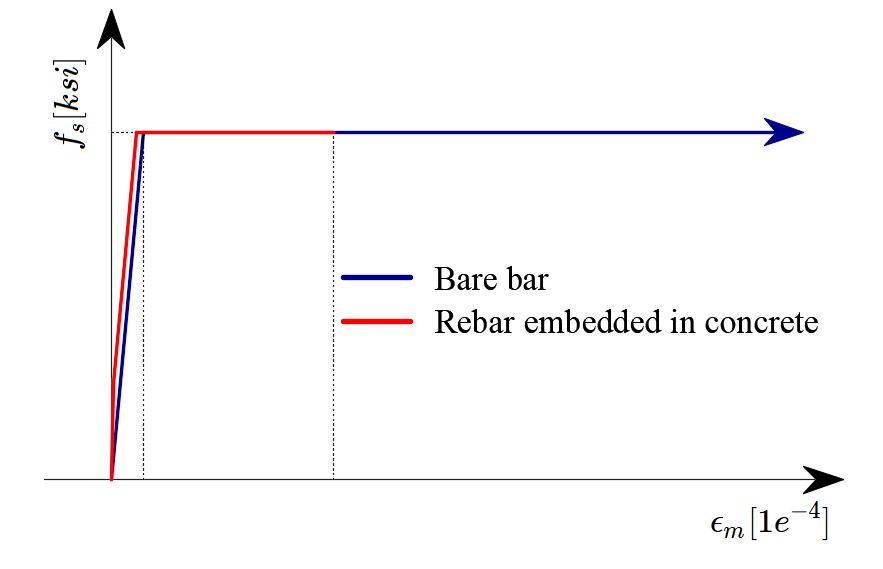
The bilinear stress-strain diagram for reinforcement bars, as defined by design codes (Fig. 1d), represents an idealized model. This model necessitates knowledge of the basic properties of the reinforcement during the design phase, specifically the strength and ductility class. Alternatively, users have the option to define a customized stress-strain relationship.

Tension stiffening is considered by modifying the stress-strain relationship of the bare reinforcing bar to capture the average stiffness of the bars embedded in the concrete (ε_m) (Fig 1b).

Anchorage

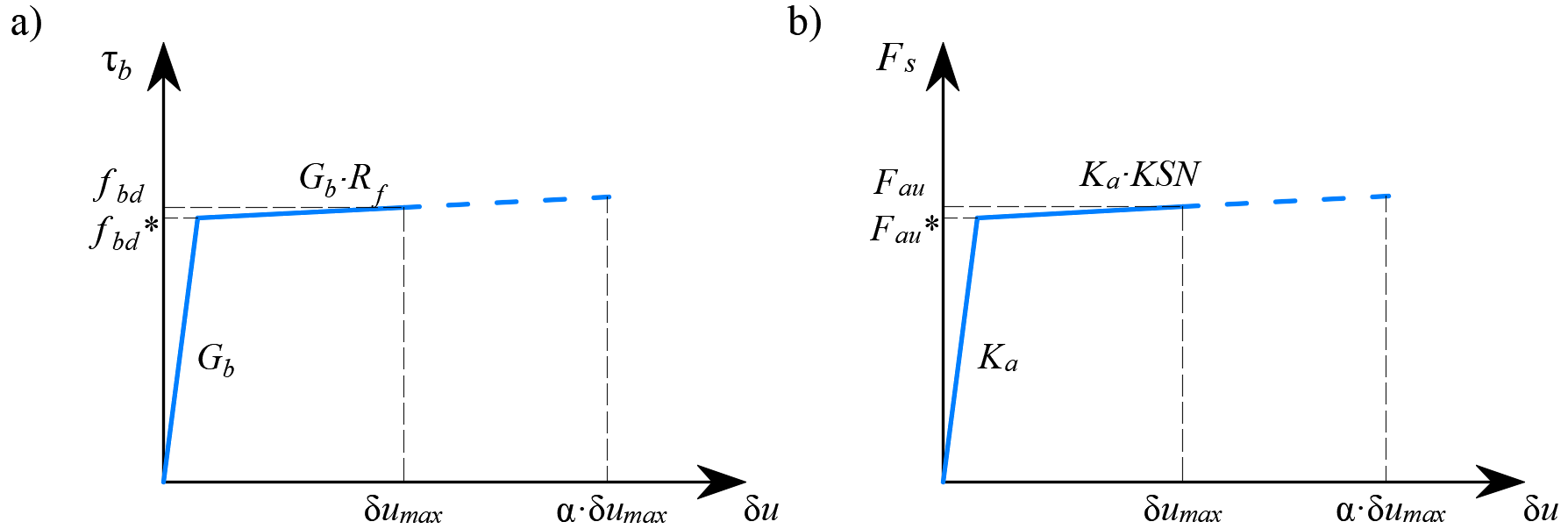
Bond-slip between reinforcement and concrete is introduced in the finite element model by considering the simplified rigid-perfectly plastic constitutive relationship presented in (Fig. 1f), with f_bd being the design value (factored value) of the ultimate bond stress specified by the design code for the specific bond conditions.

This is a simplified model with the sole purpose of verifying bond prescriptions according to design codes (i.e., anchorage of reinforcement). The reduction of the anchorage length when using hooks, loops, and similar bar shapes can be considered by defining a certain capacity at the end of the reinforcement, as will be described further.

Anchors

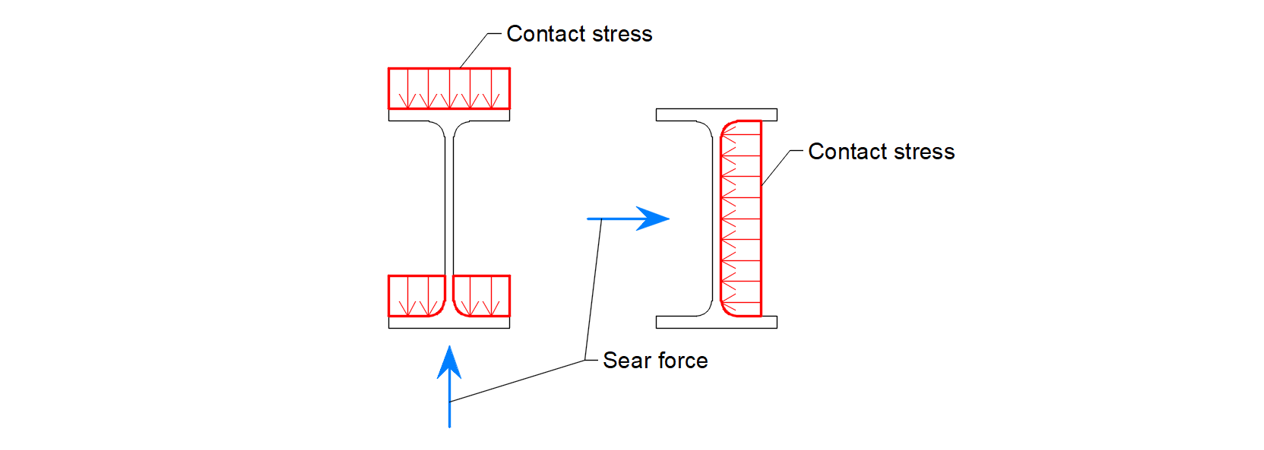
The element of the anchor is defined as being able to transfer normal tensile or compression forces, as well as shear forces, considering the bending stiffness.

The following types of anchors are available:

Cast-in-place anchors
- Reinforcement
- Washer plate
- Headed stud
Cast-in-place reinforcement
- Reinforcement
- Threaded rods

Cast-in-place - Reinforcement

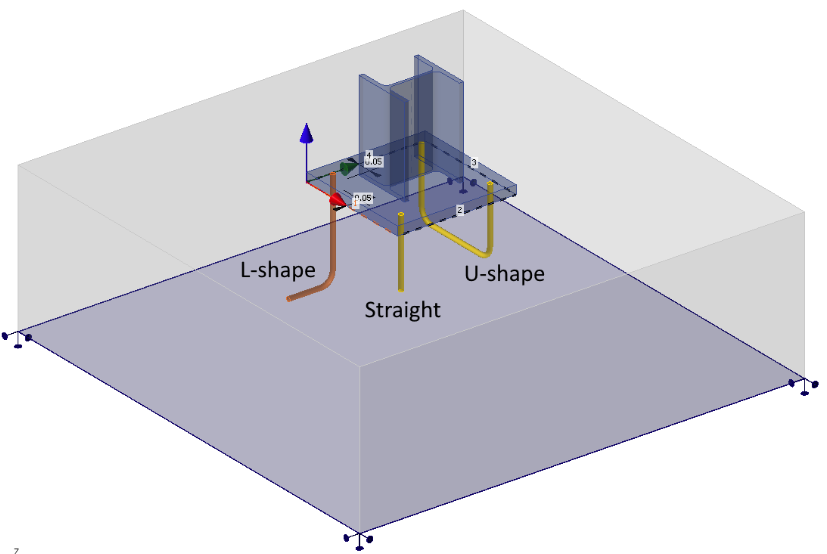
Modeled as ribbed reinforcement embedded in concrete. Bond strength is calculated according to selected code rules in the same way as for standard reinforcement. At the anchor end, an Anchorage type can be defined, working identically to reinforcement - an anchorage spring is applied with the β-factor set according to the chosen code. Three geometric shapes are available: Straight, L-shape, U-shape.

\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Cast-in reinforcement anchor - shapes}}}\]

Cast-in-place - Washer plate and Headed stud

The washer plate and the head of the headed stud are modeled as a plate-shell element from the corresponding material attached directly to the anchor shank. It transfers load to the concrete through compression-only contact. Available shapes: circular and square (only circular for headed stud), with customizable dimensions. The washer plate and head model is elastic and is not checked for resistance.

At the finite element model level, the pull-out of the anchor is directly checked. The compression contact has stop criteria set so that it is not able to transfer greater contact stress to the concrete than prescribed by the selected standard. In practical terms, this means that if the anchor were to be loaded with a force that does not comply with the pull-out assessment, the result would be premature termination of the calculation because this stop criterion would be exceeded during further loading.

The anchor shank has zero bond strength – all load is transferred to the concrete through the plate or head into the concrete.

Post-installed - Reinforcement and Threaded rod

Designed as bars installed into drilled holes and bonded with adhesive. The engineer specifies the design bond strength directly from the technical specification of the adhesive product.

More information about connecting individual anchor types to the base plate or cast-in plate can be found in the chapter Finite elements types - Load transferring devices.

Mohr-Coulomb plasticity theory implementation in 3D CSFM

In the following chapter, we will take a look at how the Mohr-Coulomb theory is implemented in 3D CSFM. We will explain how the confinement effect (triaxial stress) is considered and how the Equivalent Principal Stress σ_c,eq is calculated, which is used to determine the load-bearing capacity from the point of view of concrete.

Introduction to the theory

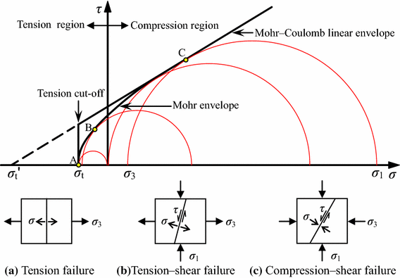
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials, to shear and normal stress. Most of the classical engineering materials follow this rule in at least a part of their shear failure envelope. Generally, the theory applies to materials for which the compressive strength far exceeds the tensile strength.

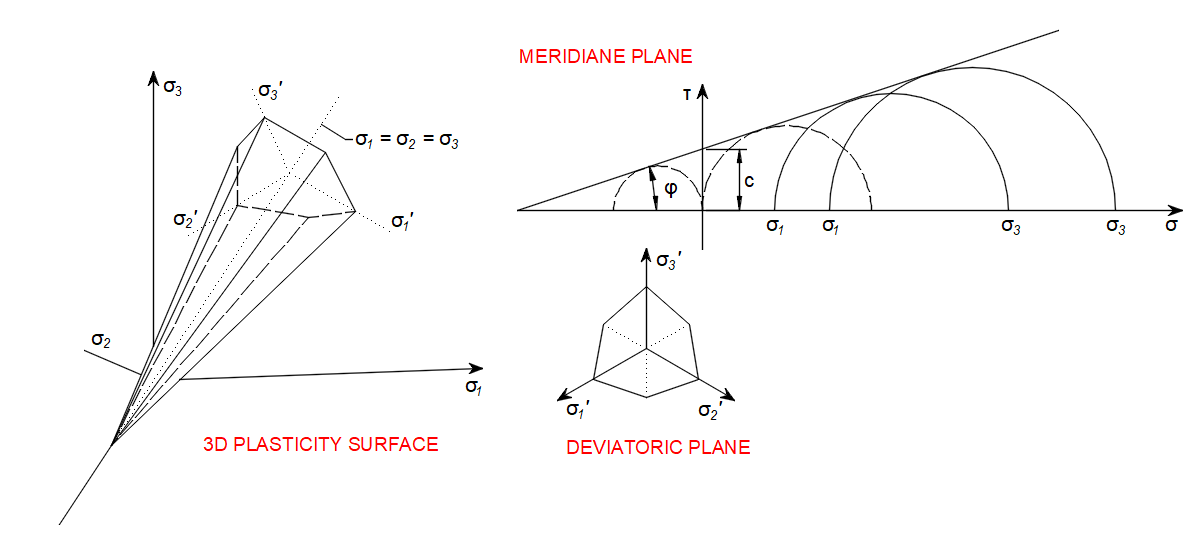
\[ \textsf{\textit{\footnotesize{Fig. 4\qquad Mohr-Coulomb Plasticity Model }}}\]

In structural engineering, it is used to determine failure load as well as the angle of fracture for displacement of fracture surface in concrete and similar materials. Coulomb's friction hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. Mohr's circle is used to determine which principal stresses will produce this combination of shear and normal stress and the angle of the plane in which this will occur. According to the principle of normality, the stress introduced at failure will be perpendicular to the line describing the fracture condition.

\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Meridian plane and tension cut-off}}}\]

It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the angle of friction. This makes the strength of the material determinable by comparing the external mechanical work introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By conservation of energy, the sum of these must be zero and this will make it possible to calculate the failure load of the construction.

Implementation in 3D CSFM

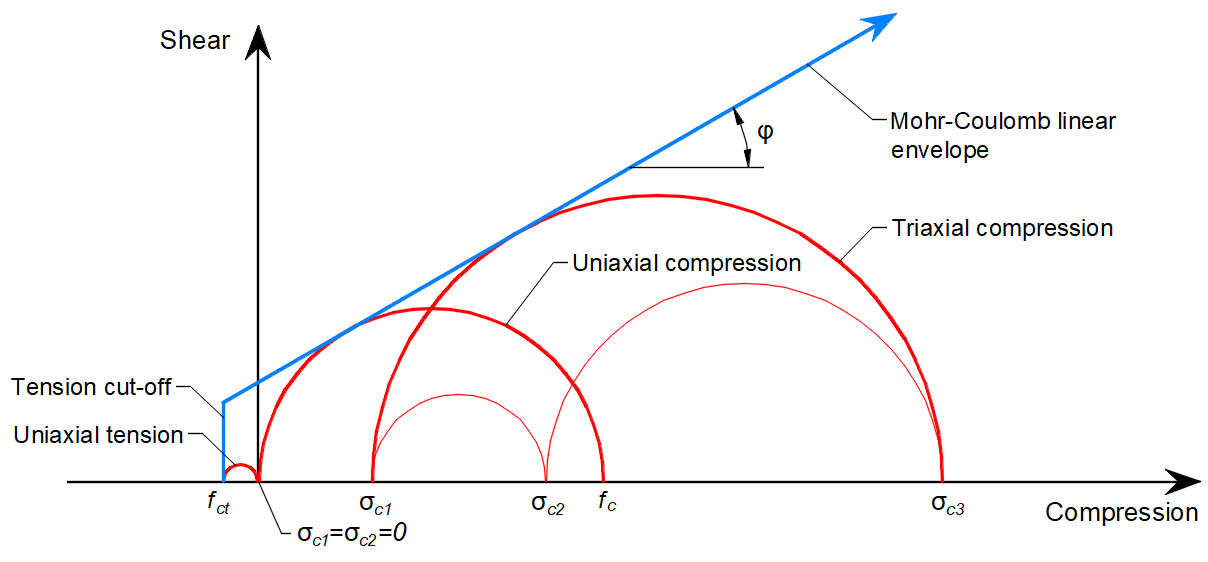
In general, for a given angle of internal friction of the concrete, which is around φ = 30-40° in Reference [1], [2], [3], [4], the tensile and compressive strengths of the concrete Mohr's circles can be constructed as in Figure 6.

\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Mohr's circles for concrete}}}\]

Where f_c is concrete strength in compression, f_ct is concrete strength in tension, φ is the angle of internal friction, and σ_c₁, σ_c₃ are the principal stresses of concrete under triaxial compression.

It can be noticed that as the principal stress σ_c₃ increases, the maximal possible difference between the values of σ_c₃ and σ_c₁, which we define as maximal σ_c,eq (see below), also increases. This difference corresponds to twice the deviatoric stress defined in the literature as a radius of the mohr circles.

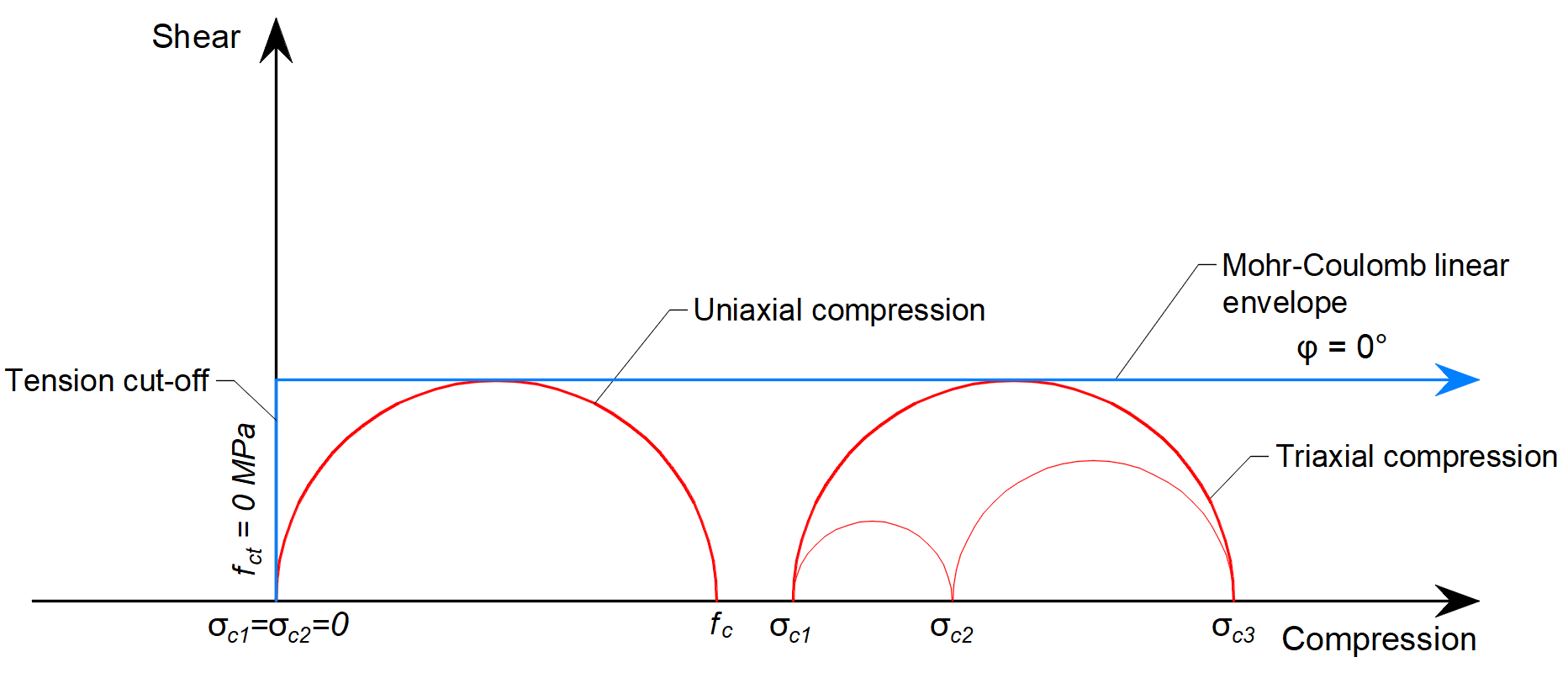
In 3D CSFM implemented in IDEA StatiCa Detail, the angle of internal friction is considered as φ = 0°, as shown in Figure 7.

\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Mohr's circles for concrete implemented in IDEA StatiCa Detail}}}\]

The practical consequence of this implementation is that the maximum difference between σ_c₃ and σ_c₁ is constant as σ_c₃ increases.

Equivalent Principal Stress expresses the equivalent uni-axial stress for a general tri-axial stress state.

\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]

The σ_c,eq value can, therefore, be directly compared with uniaxial strength limits according to codes.

\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} \le 1\]

Where σ_c_,lim is the design (factored) uniaxial strength of concrete f_c.

Comparing Figure 6, where the real angle of internal friction is used, and Figure 7, which shows the Mohr-Coulomb theory implementation with zero angle of internal friction, it can be seen that the approach chosen for the calculations in Detail is very conservative for the assessment of triaxial stress state.

For a better understanding of the areas affected by tri-axial compression stress, the expression of the increase of the effective material strength due to tri-axial compression has been added to the IDEA StatiCa Detail application as a ratio σ_c₃/σ_c,lim. You can find this ratio in the Strength code check.

In the Auxiliary results, the user can also find the κ factor, which explains the tri-axiality in a different way.

\[\kappa = \frac{ \sigma_{c3}}{ \sigma_{c,eq}}\]

The concrete strength check can be then rewritten as:

\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} = \frac{\sigma_{c,3} }{ \kappa \cdot \sigma_{c,lim}} \le 1\]

It follows from the previous that if the element is under hydrostatic stress - σ_c₃=σ_c₂=σ_c₁, the Equivalent Principal Stress σ_c,eq will have the zero value, and the kappa factor will reach infinity.

More can be found here: Tri-axial stress – the active confinement effect

General mechanics assumptions for 3D CSFM

Equilibrium equations

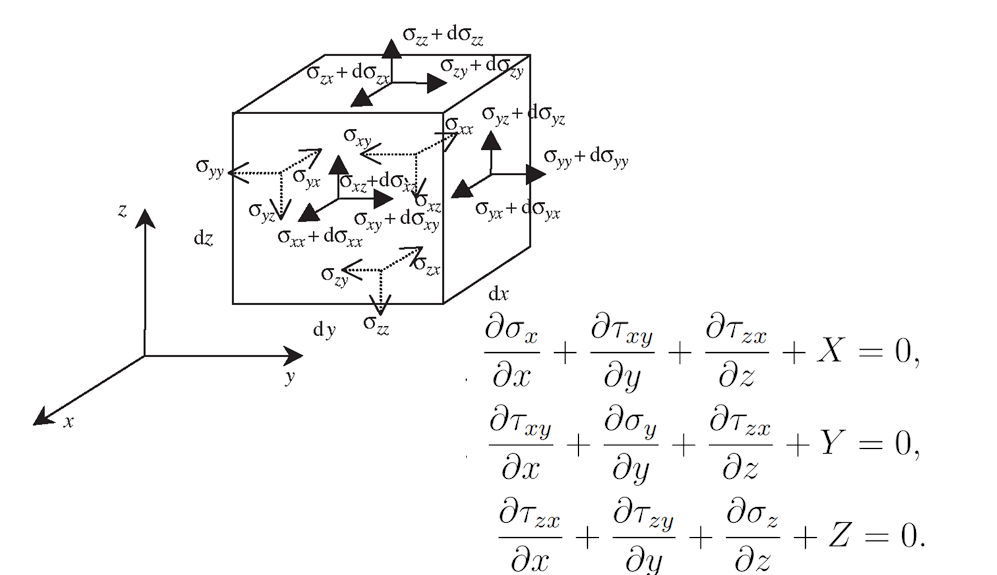
The theory of small deformations enables the assembly of the equilibrium equation based on the undeformed volume using a first-order approach.

\[ \textsf{\textit{\footnotesize{Fig. 8\qquad Equilibrium equations and graphical representation on infinitesimal element}}}\]

Compatibility equations

A solid body comprises infinitesimal volumes or material points, each of which is interconnected without gaps or overlaps. Mathematical conditions must be adhered to in order to prevent the occurrence of gaps or overlaps when a continuum body undergoes deformation.

Constitutive equations

The constitutive equations governing the behavior of 3D elements play a pivotal role in the analysis of material behavior in structural mechanics. These equations are formulated to accommodate the non-linear isotropic behavior, which is valid for solid block members in IDEA StatiCa Detail.

\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Linearly elastic isotropic compliance matrix}}}\]

Analysis model of IDEA StatiCa 3D Detail

Introducción a la aplicación de elementos finitos

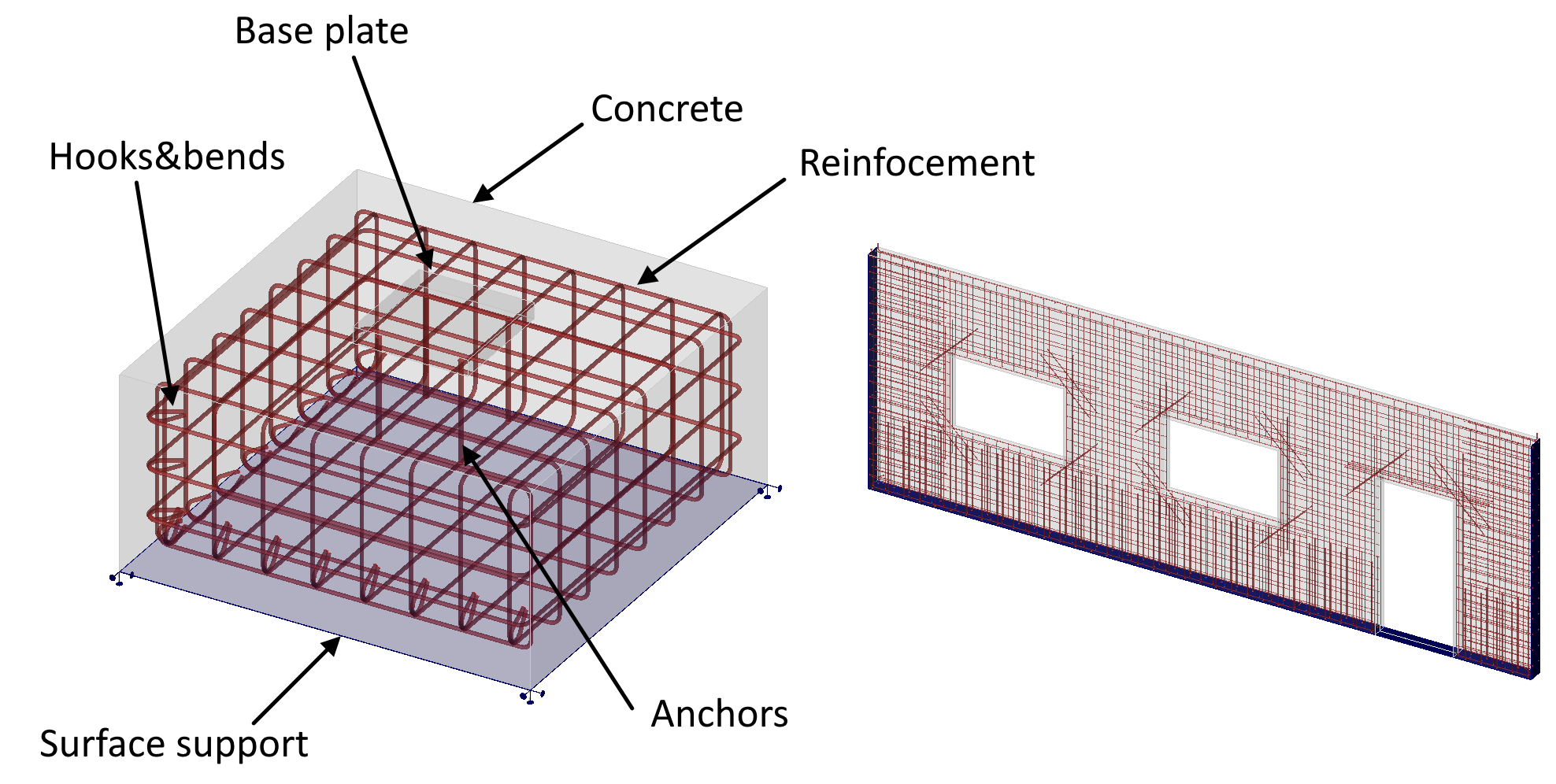
El CSFM 3D considera campos de tensión continuos en el hormigón (elementos finitos 3D), complementados por elementos discretos de "varilla" que representan la armadura (elementos finitos 1D). Por lo tanto, la armadura no se incrusta difusamente en los elementos finitos 3D del hormigón, sino que se modela explícitamente y se conecta a ellos.

\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Representación del modelo de cálculo para bloque de hormigón y muro fuera del plano}}}]

Tipos de elementos finitos

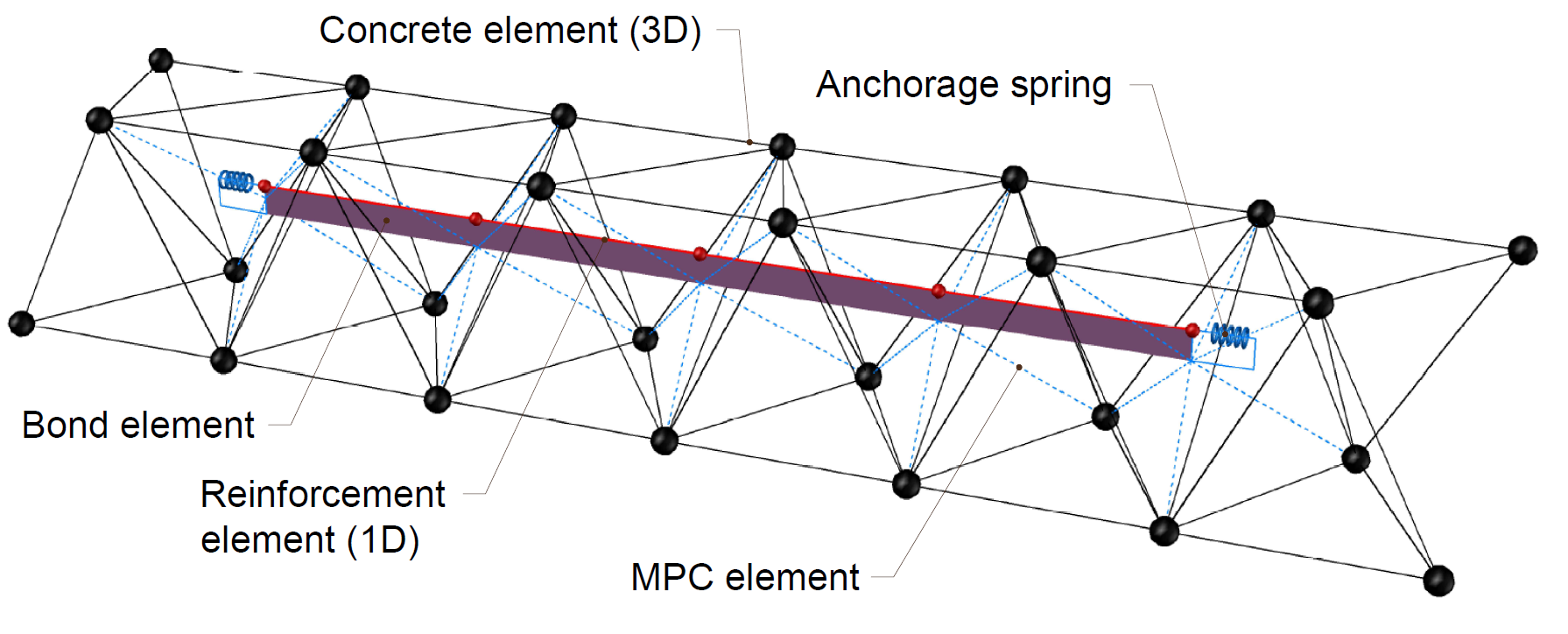
El modelo de análisis de elementos finitos no lineal (inelástico) se crea mediante varios tipos de elementos finitos utilizados para modelizar el hormigón, la armadura y la unión entre ellos. Los elementos de hormigón y armadura se mallan primero de forma independiente y luego se interconectan mediante restricciones multipunto (elementos MPC). Esto permite que la armadura ocupe cualquier posición no limitada a los nodos de la malla tetraédrica. Para verificar la longitud de anclaje, la unión y el extremo de anclaje se insertan elementos de muelle entre la armadura y los elementos MPC.

\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Modelo de elementos finitos: elementos de refuerzo mapeados a la malla de hormigón utilizando elementos MPC y de enlace}} {}]

Hormigón

El hormigón se analiza utilizando elementos tetraédricos mixtos con rotaciones nodales. Los elementos tetraédricos nos permiten mallar regiones de cualquier topología mientras que la formulación implementada garantiza resultados de deformación precisos (sin esfuerzos cortantes espurios conocidos como efecto shear lock) incluso para la malla gruesa que no sería adecuada para la formulación de elementos tetraédricos lineales.

Se utiliza la integración completa. Esto significa que cada elemento está equipado con cuatro puntos de integración situados dentro del volumen. Esta integración permite obtener un campo de deformaciones y tensiones preciso, lo que permite evaluar y presentar los resultados de forma suficiente en todo el volumen. Posteriormente, los criterios de parada se establecen en función del valor en el punto de integración.

Refuerzo

Las armaduras se modelizan mediante elementos "varilla" 1D de dos nodos (CROD), que sólo tienen rigidez axial. Estos elementos están conectados a elementos especiales de "unión" que se desarrollaron para modelar el comportamiento de deslizamiento entre una barra de refuerzo y el hormigón circundante. Estos elementos de unión se conectan posteriormente mediante elementos MPC (restricción multipunto) a la malla que representa el hormigón. Este planteamiento permite el mallado independiente de la armadura y el hormigón, mientras que su interconexión se garantiza posteriormente.

Elementos de unión

La longitud de anclaje se verifica implementando los esfuerzos cortantes de enlace entre los elementos de hormigón (3D) y los elementos de armadura (1D) en el modelo de elementos finitos. Para ello, se ha desarrollado el tipo de elemento finito "enlace".

El elemento de unión se define como un elemento finito de cáscara conectado a los elementos que representan el refuerzo por la primera capa y por la segunda capa a la malla de hormigón mediante restricciones multipunto (elementos MPC). Cabe señalar que el elemento de unión siempre se muestra en este artículo con una altura distinta de cero, que, sin embargo, se define como infinitesimal en el modelo.

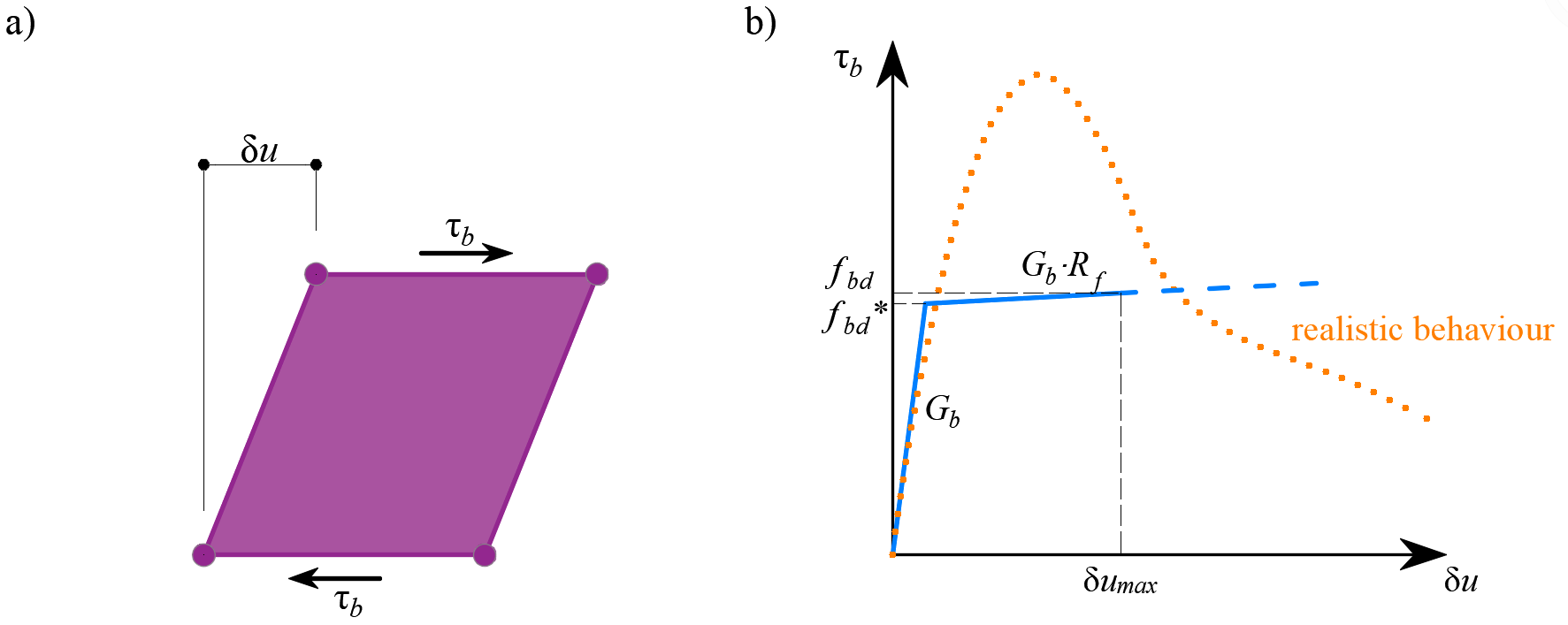
El comportamiento de este elemento se describe por la tensión de adherencia, _τb, como una función bilineal del deslizamiento entre los nudos superior e inferior, δu, ver (Fig. 11).

\[ \textsf{\textit{footnotesize{Fig. 11\qquad (a) Ilustración conceptual de la deformación de un elemento de unión; (b) función cizalladura-deformación}}}]

El módulo de rigidez elástica de la relación adherencia-deslizamiento, Gb, se define como sigue:

\[G_b = k_g \cdot \frac{E_c}{Ø}]

coeficiente kg en función de la superficie de la barra de armadura (por defecto kg = 0,2)

_Ec módulo de elasticidad del hormigón (tomado como Ecm en el caso de EN)

Ø diámetro de la armadura

Para verificar la longitud de anclaje se utilizan los valores de cálculo (valores factorizados) del esfuerzo cortante último de adherencia, _fbd, proporcionados en los respectivos códigos de cálculo seleccionados EN 1992-1-1 o ACI 318-19. El endurecimiento de la rama plástica se calcula por defecto como Gb/105.

Muelle de anclaje

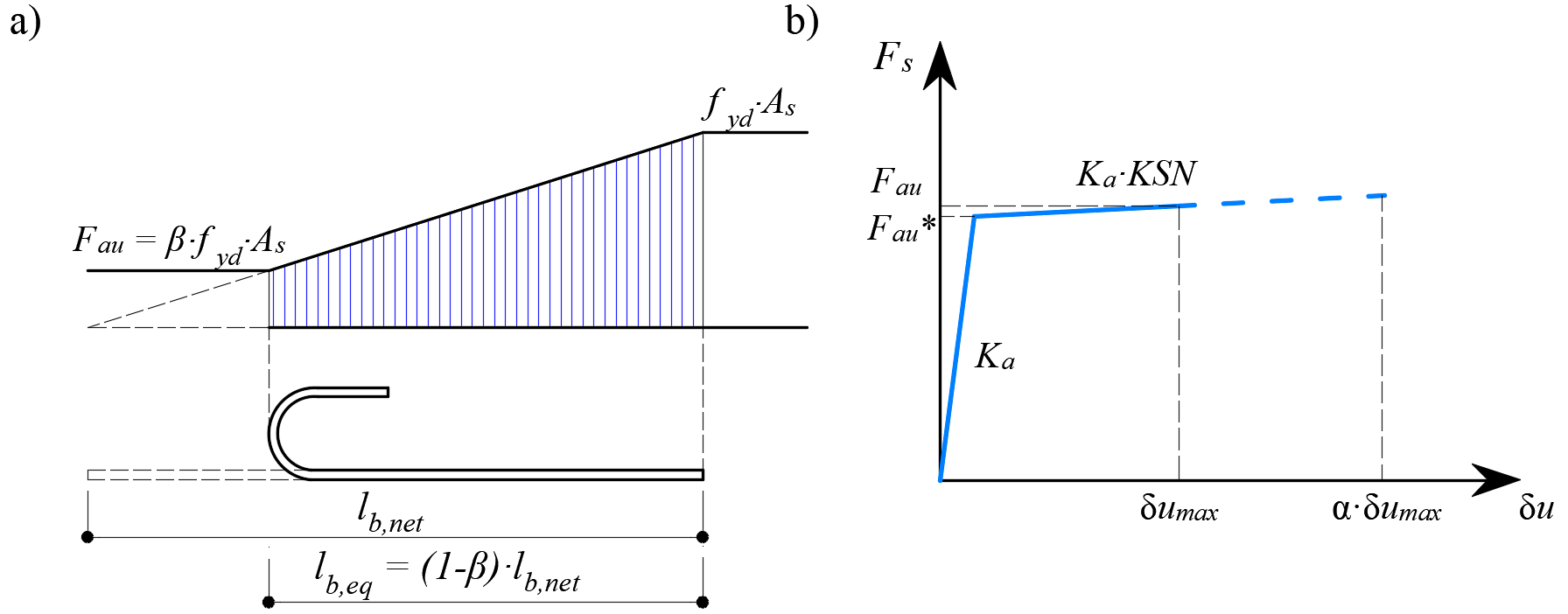
La provisión de extremos de anclaje a las barras de armadura (es decir, codos, ganchos, lazos...), que cumple las prescripciones de los códigos de diseño, permite reducir la longitud de anclaje básica de las barras(lb_,net) en un determinado factor β (denominado a continuación "coeficiente de anclaje"). El valor de diseño de la longitud de anclaje(lb) se calcula entonces de la siguiente manera:

\[ \textsf{\textit{footnotesize{Fig. 12\qquad Modelo para la reducción de la longitud de anclaje: a) Fuerza de anclaje a lo largo de la longitud de anclaje de }}}]. \[ \textsf{textit{footnotesize{la barra de refuerzo, b) ley constitutiva de la fuerza de deslizamiento-anclaje}}}]

La reducción de la longitud de anclaje se incluye en el modelo de elementos finitos mediante un elemento muelle en el extremo de la barra (Fig. 12a), que viene definido por el modelo constitutivo mostrado en (Fig. 12b). La fuerza máxima transmitida por este muelle(_Fau) es:

\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]

donde :

β el coeficiente de anclaje en función del tipo de anclaje

_Como la sección transversal de la barra de refuerzo

_fyd el valor de cálculo (valor factorizado) del límite elástico de la armadura

Dispositivos de transferencia de carga

Placa base

La placa base se modela como un elemento de envolvente lineal. El material de acero utilizado para las placas base se define en la pestaña Materiales. La única propiedad física es el módulo de elasticidad E.

\[ \textsf{\textit{footnotesize{Fig. 13\qquad Definición del material de la placa base}}]

La placa base puede ser cargada por la carga puntual (Fx, Fy, Fz, Mx, My, Mz) y grupo de fuerzas (Fx, Fy, Fz), principalmente utilizado para cargar modelos exportados desde la Conexión IDEA StatiCa. Tenga en cuenta que las cargas y momentos puntuales cargan directamente el nodo correspondiente de la placa base. Esto significa que no hay redistribución, sólo por la rigidez de la placa base.

Esta implementación permite importar efectos de carga desde IDEA StatiCa Connection que se aplican a la placa base en la ubicación de los elementos finitos de soldadura individuales con el valor y la dirección determinados a partir de la tensión general de ese elemento finito de soldadura. Se puede leer más en el capítulo correspondiente de este documento.

Entre la placa base y el hormigón se define un contacto de sólo compresión por fricción. Para la transferencia a cortante el usuario puede elegir entre tres opciones:

Por anclajes
Por fricción
Por orejeta de cizallamiento

El software no permite la combinación de estos mecanismos de transferencia de cizalladura.

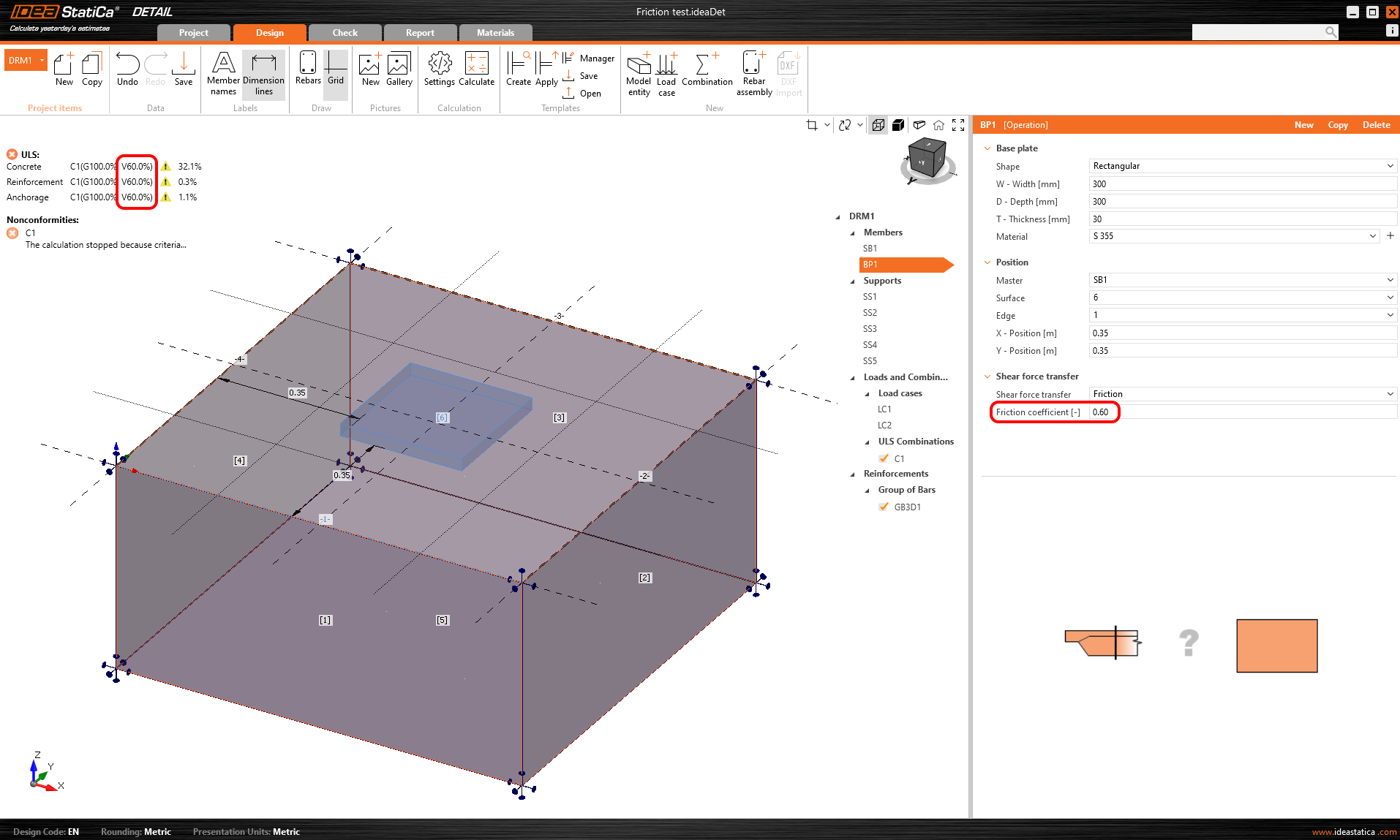
El coeficiente de fricción debe introducirse como valor de diseño (factorizado). En caso de que la fuerza cortante resultante _Fxy exceda la fuerza de presión _Fz veces el coeficiente de fricción μ el cálculo se detendrá y no todas las cargas se aplicarán al modelo. La condición se escribe de la siguiente manera:

\[\frac {F_{xy}}{ \mu \cdot F_{z}}le 1\]

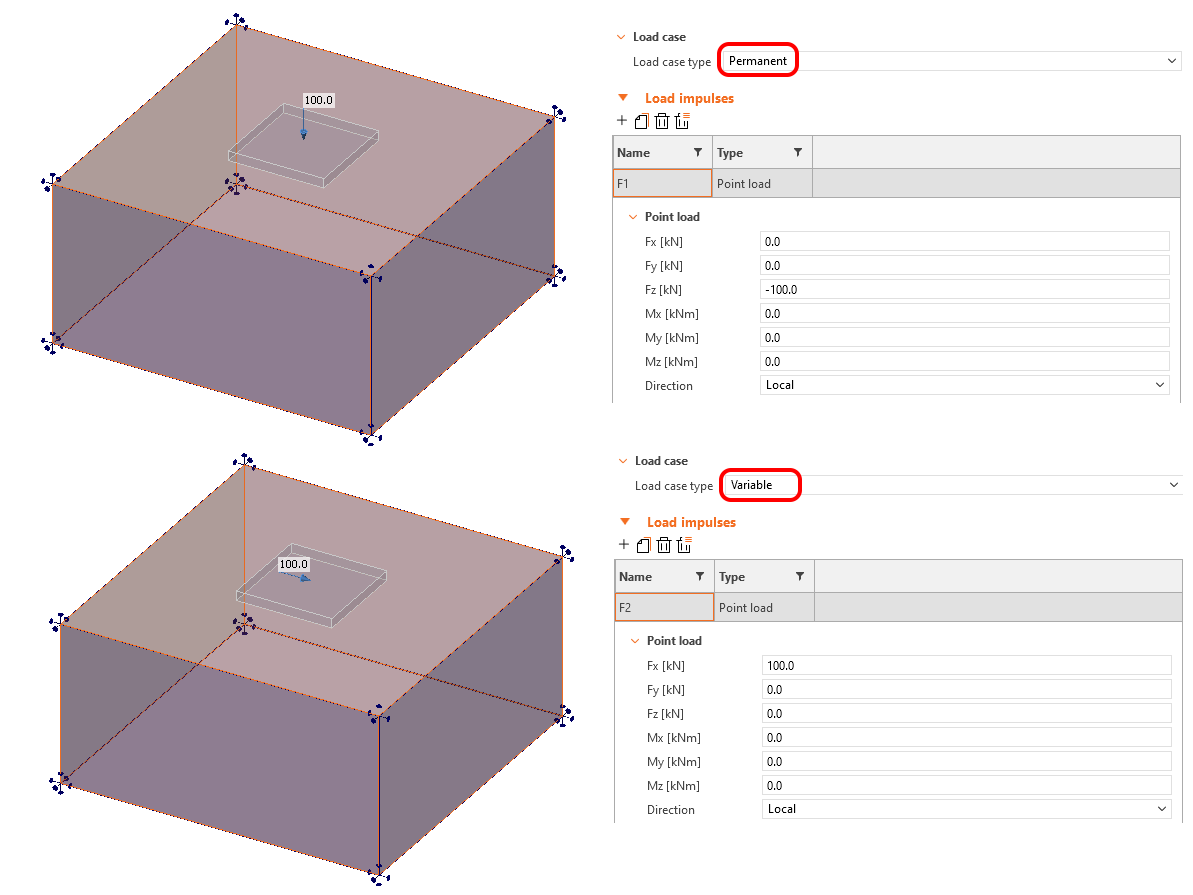
Esto se puede ver en el siguiente ejemplo en el que se consideran dos casos de carga.

LC1 - Tipo permanente - _Fz = 100 kN
LC2 - Tipo variable - _Fx = 100 kN

\[ \textsf{\textit{footnotesize{Fig. 14\qquad Entrada de carga para el ejemplo que explica la transferencia de cortante por fricción}}]

En el primer paso del cálculo, se aplica toda la carga permanente. A continuación, se aplica gradualmente la carga variable hasta alcanzar el valor de la carga de presión multiplicado por el coeficiente de fricción.

\[ \textsf{\textit{footnotesize{Fig. 15\qquad Resultados del ejemplo que explica la transferencia de cizalladura por fricción}}]

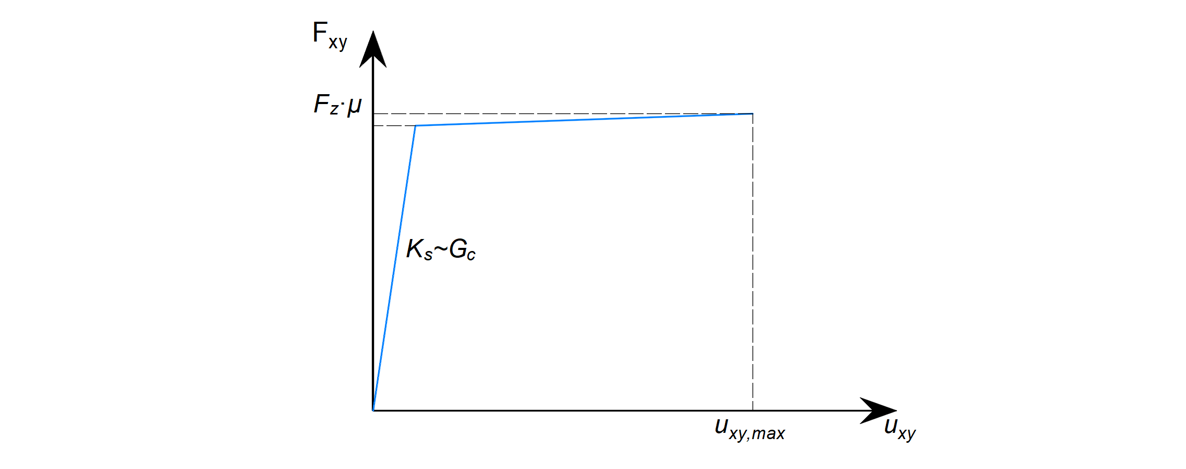
El gráfico de la Figura 16 define el comportamiento del contacto por fricción entre la placa base y el hormigón.

\[ \textsf{\textit{footnotesize{Fig. 16\qquad Gráfico fuerza-desplazamiento que describe el comportamiento del contacto por rozamiento}}]

El valor de Fzμ difiere para cada incremento del cálculo, mientras que el valor de la deformación máxima por cizalladura _uxy es constante.

Si la fuerza normal de compresión _Fz y la fuerza de corte _Fxy se introducen en un tipo de caso de carga (por ejemplo, sólo permanente), y la condición de _Fxy / (_Fzμ) ≤ 1 no se cumple, no se aplicará ninguna carga al modelo porque la condición no se cumple en ningún incremento del cálculo.

La orejeta de cortante está conectada con la malla de hormigón mediante restricciones que sólo permiten la transferencia de tensiones normales a compresión.

\[ \textsf{\textit{footnotesize{Fig. 17\qquad Transferencia de la orejeta de cortante del mecanismo de cortante}}]

La orejeta de cizallamiento se modela a partir de elementos lineales de concha, donde el módulo de elasticidad E define el material.

Los resultados no se evalúan y se muestran tanto para la placa base como para la orejeta de cizallamiento.

Anclajes

Los elementos finitos que representan los anclajes se modelan para poder transferir fuerzas normales y cortantes al hormigón, teniendo en cuenta también la rigidez a flexión de los anclajes. Para modelizar el deslizamiento entre el anclaje y el hormigón circundante, se utilizan los mismos elementos de adherencia y MPC que para la armadura. Con la diferencia de que para los anclajes adhesivos es posible especificar la resistencia de adherencia de diseño.

Los anclajes pueden interconectarse con placas base. Para esta interconexión, se utiliza una restricción totalmente no lineal para conectar el extremo del anclaje y un nodo de la placa base. Este elemento nos permite controlar todos los grados de libertad para garantizar, por ejemplo, que los anclajes no transmitan presión a la placa base sin separación, o que el anclaje no transmita cizalladura al modelar una orejeta de cizalladura, etc.

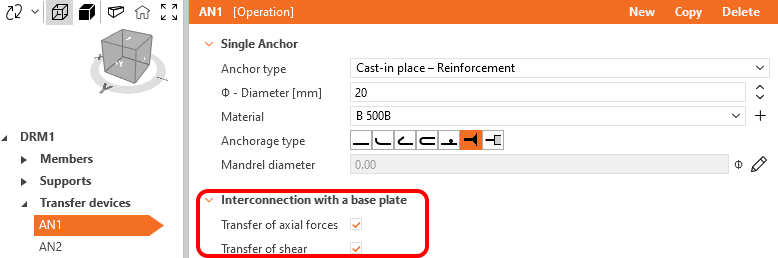
Los ajustes deinterconexión con la placa base para anclajes permiten al usuario controlar si el anclaje se conectará con la placa base mediante la restricción mencionada anteriormente y cómo.

En la versión actual sólo se admite el contacto directo entre la placa base y el hormigón .

La fuerza de compresión no se transfiere de la placa base al anclaje en el caso de Contacto directo. La compresión se transfiere sólo por el contacto entre la placa base y el hormigón.

La casilla de verificación Transferencia de fuerzas axiales puede utilizarse para controlar si el anclaje y la placa base estarán conectados o no en términos de tensión. Esto se utiliza principalmente para la exportación de la función Conexión (véase el capítulo correspondiente). Para el modelado manual, tiene sentido tener esta casilla de verificación siempre marcada.

La casilla de verificación Transferencia de cortante puede utilizarse para controlar si el anclaje y la placa base se conectarán o no en términos de cortante. Tenga en cuenta que no se admite la combinación de mecanismos de transferencia de esfuerzo cortante, por lo que para la transferencia por fricción y la orejeta de esfuerzo cortante, esta casilla de verificación es irrelevante. Por otro lado, para la transferencia a cortante mediante anclajes, este campo da la opción de excluir algunos anclajes de la transferencia a cortante.

Malla de hormigón en 3D CSFM

Los elementos finitos se implementan internamente, y el modelo de análisis se genera automáticamente sin necesidad de una interacción competente del usuario. Una parte importante de este proceso es el mallado.

Hormigón

Todos los elementos de hormigón se mallan juntos. La aplicación calcula automáticamente un tamaño de elemento recomendado basándose en el tamaño y la forma de la estructura y teniendo en cuenta el diámetro de la barra de refuerzo más grande. Además, el tamaño de elemento recomendado garantiza la generación de un mínimo de cuatro elementos en las partes delgadas de la estructura, como pilares esbeltos o muros finos, para garantizar resultados fiables en estas zonas. Los diseñadores siempre pueden seleccionar un tamaño de elemento de hormigón definido por el usuario modificando el multiplicador del tamaño de malla por defecto.

Armadura

La armadura se divide en elementos con aproximadamente la misma longitud que el tamaño del elemento de hormigón. Una vez generadas las mallas de armadura y hormigón, se interconectan con elementos de unión, como se muestra en la Fig. 9.

Refinado

La malla de hormigón se refina automáticamente bajo la placa base, alrededor de los anclajes y alrededor de las orejetas de cortante. El tamaño de la malla refinada es por defecto dos veces menor que la malla básica de hormigón. El radio del área refinada se define como el tamaño del elemento multiplicado por dos.

Método de solución y algoritmo de control de carga para CSFM 3D

Se utiliza un algoritmo Newton-Raphson (NR) estándar completo para encontrar la solución a un problema MEF no lineal.

Generalmente, el algoritmo NR no suele converger cuando se aplica toda la carga en un solo paso. Un enfoque habitual, que también se utiliza aquí, es aplicar la carga secuencialmente en múltiples incrementos y utilizar el resultado del incremento de carga anterior para iniciar la solución Newton del siguiente. Para ello, se implementó un algoritmo de control de carga sobre el Newton-Raphson. En caso de que las iteraciones NR no converjan, el incremento de carga actual se reduce a la mitad de su valor y se vuelven a intentar las iteraciones NR.

Un segundo objetivo del algoritmo de control de carga es encontrar la carga crítica, que corresponde a determinados "criterios de parada", en concreto, la deformación máxima del hormigón, el deslizamiento máximo de los elementos de unión, el desplazamiento máximo de los elementos de anclaje y la deformación máxima de las barras de refuerzo. La carga crítica se determina mediante el método de bisección. En caso de que se supere el criterio de parada en algún punto del modelo, se descartan los resultados del último incremento de carga y se calcula un nuevo incremento de la mitad de tamaño que el anterior. Este proceso se repite hasta que se encuentra la carga crítica con una cierta tolerancia de error.

Para el hormigón, el criterio de parada se fijó en una deformación del 5% en compresión (es decir, alrededor de un orden de magnitud mayor que la deformación de fallo real del hormigón) y del 7% en tracción en los puntos de integración de los elementos de cáscara. En tracción, el valor se fijó para permitir que se alcanzara primero la deformación límite en la armadura, que suele estar en torno al 5% sin tener en cuenta la rigidización por tracción. En compresión, el valor se eligió entre varias alternativas como uno lo suficientemente grande para que los efectos del aplastamiento sean visibles en los resultados, pero lo suficientemente pequeño para no causar demasiados problemas con la estabilidad numérica.

\[ \textsf{\textit{footnotesize{Fig 13\qquad Ley constitutiva de los elementos de enlace y anclaje utilizados para la verificación de la longitud de anclaje: a) Tensión de cizalladura de enlace}}] \respuesta al deslizamiento de un elemento de unión, b) respuesta fuerza-desplazamiento de un elemento de anclaje}}.

Para el refuerzo, el criterio de parada se define en términos de tensiones. Dado que se modelizan las tensiones en la fisura, el criterio en tracción corresponde a la resistencia a tracción de la armadura teniendo en cuenta el coeficiente de seguridad. El mismo valor se utiliza para el criterio en compresión.

El criterio de detención en elementos de unión y muelles de anclaje es _α-δumax, donde _δumax es el deslizamiento máximo utilizado en las comprobaciones del código y α = 10.

Presentación de resultados en 3D

Los resultados se presentan independientemente para el hormigón y para los elementos de refuerzo. Los valores de tensión y deformación en el hormigón se calculan en los puntos de integración de los elementos de volumen. Sin embargo, como no resulta práctico presentar los datos de esta manera, los resultados se presentan por defecto en nudos, como el valor máximo de la tensión de compresión a partir de puntos de integración de Gauss adyacentes en elementos conectados. Debe tenerse en cuenta que esta representación podría subestimar localmente los resultados en los bordes comprimidos de las barras en un caso en el que el tamaño del elemento finito sea similar a la profundidad de la zona de compresión.

Los resultados de los elementos finitos de refuerzo son constantes para cada elemento (un valor - por ejemplo, para las tensiones del acero) o lineales (dos valores - para los resultados de las uniones). Para los elementos auxiliares, como los elementos de las placas de apoyo, sólo se presentan las deformaciones.

Modelo importado de IDEA StatiCa Connection

El modelo IDEA Statica Detail no siempre tiene que ser modelado desde cero o desde una plantilla. También existe la opción de importar el modelo incluyendo los efectos de carga desde IDEA StatiCa Connection. La geometría del bloque de hormigón, los anclajes, la placa base, los materiales y los efectos de carga se transfieren.

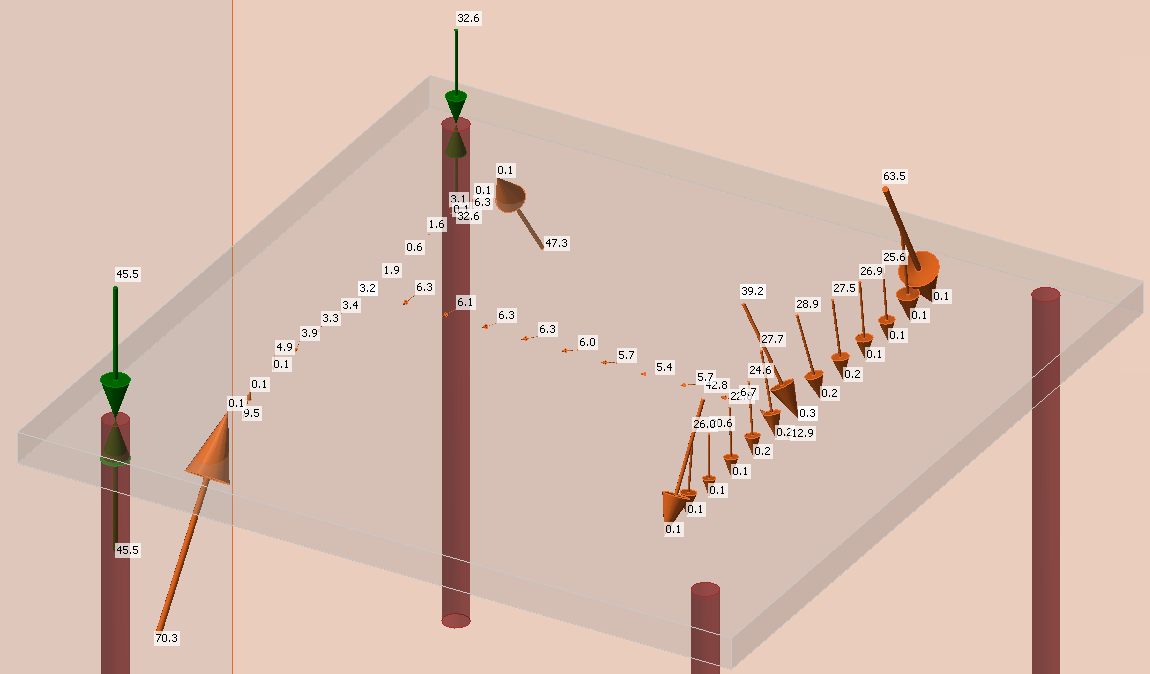
\[ \textsf{\textit{footnotesize{Fig. 16\qquad Cargas importadas desde IDEA StatiCa Connection}}}]

La placa base está cargada por un grupo de fuerzas determinadas a partir de la tensión general de cada elemento finito de las soldaduras que conectan el miembro de acero y la placa base.

Dado que la definición de los componentes individuales es diferente en Conexión y Detalle (por ejemplo, la placa base se modela mediante un material lineal en Detalle mientras que en Conexión se modela mediante un material plástico), habría una redistribución diferente de las cargas entre el contacto placa base-hormigón y los anclajes, o entre los propios anclajes. En otras palabras, habría diferentes fuerzas normales de tracción en los anclajes en Conexión y Detalle. Por este motivo, los anclajes se importan desconectados para fuerzas normales (en la dirección del anclaje) de la placa base, y los anclajes se cargan directamente con las fuerzas de tracción aplicadas. Además, deben añadirse las fuerzas opuestas que cargan la placa base situada en la ubicación del anclaje para que el modelo alcance el equilibrio. Estas dos fuerzas opuestas se muestran en la figura 16.

Sin embargo, las fuerzas de cizallamiento se transfieren mediante la interconexión de la placa base y el anclaje (o orejeta de cizallamiento, o fricción). Este comportamiento es posible porque existe una restricción que conecta la placa base y el anclaje que nos permite controlar todos los grados de libertad de esta interconexión.

Model verification

Estados límite

Estado límite último

Las diferentes verificaciones exigidas por los códigos de diseño específicos se evalúan a partir de los resultados directos proporcionados por el modelo. Las verificaciones de los estados límite últimos se realizan para la resistencia del hormigón, la resistencia de la armadura y el anclaje (esfuerzos cortantes de adherencia).

Para garantizar que un elemento estructural tiene un diseño eficiente, es muy recomendable ejecutar un análisis preliminar que tenga en cuenta los siguientes pasos:

Elegir una selección de las combinaciones de carga más críticas.
Calcular sólo las combinaciones de carga de Estado Límite Último (ELU).
Para acelerar el tiempo de cálculo y resolver cualquier problema, considere la posibilidad de utilizar una malla gruesa aumentando el multiplicador del tamaño de malla por defecto en la Configuración (Fig. 14). Si el modelo funciona bien, revierta el multiplicador a un factor de 1.

\[ \textsf{\textit{footnotesize{Fig 14\qquad Multiplicador de malla}}}]

Un modelo de este tipo calculará muy rápidamente, permitiendo a los diseñadores revisar el detallado del elemento estructural de manera eficiente y volver a ejecutar el análisis hasta que se cumplan todos los requisitos de verificación para las combinaciones de carga más críticas. Una vez cumplidos todos los requisitos de verificación de este análisis preliminar, se sugiere incluir todas las combinaciones de carga última y utilizar un tamaño de malla fino (el tamaño de malla recomendado por el programa). Los usuarios pueden cambiar el tamaño de malla mediante el multiplicador, que puede alcanzar valores de 0,5 a 5 (Fig. 14).

Los resultados básicos y las verificaciones (tensión, deformación y utilización (es decir, el valor calculado/valor límite del código)), así como la dirección de las tensiones principales en el caso de elementos de hormigón) se muestran mediante diferentes gráficos donde la compresión se presenta generalmente en rojo y la tensión en azul. Se pueden resaltar los valores mínimos y máximos globales de toda la estructura, así como los valores mínimos y máximos de cada parte definida por el usuario. En una pestaña separada del programa, pueden mostrarse resultados avanzados como los valores de los tensores, las deformaciones de la estructura y las relaciones de armadura (efectiva y geométrica) utilizadas para calcular la rigidez a tracción de las barras de armadura. Además, pueden presentarse las cargas y reacciones para combinaciones o casos de carga seleccionados.

Structural verifications according to EUROCODE

Modelos de materiales en 3D CSFM (EN)

Hormigón - ULS

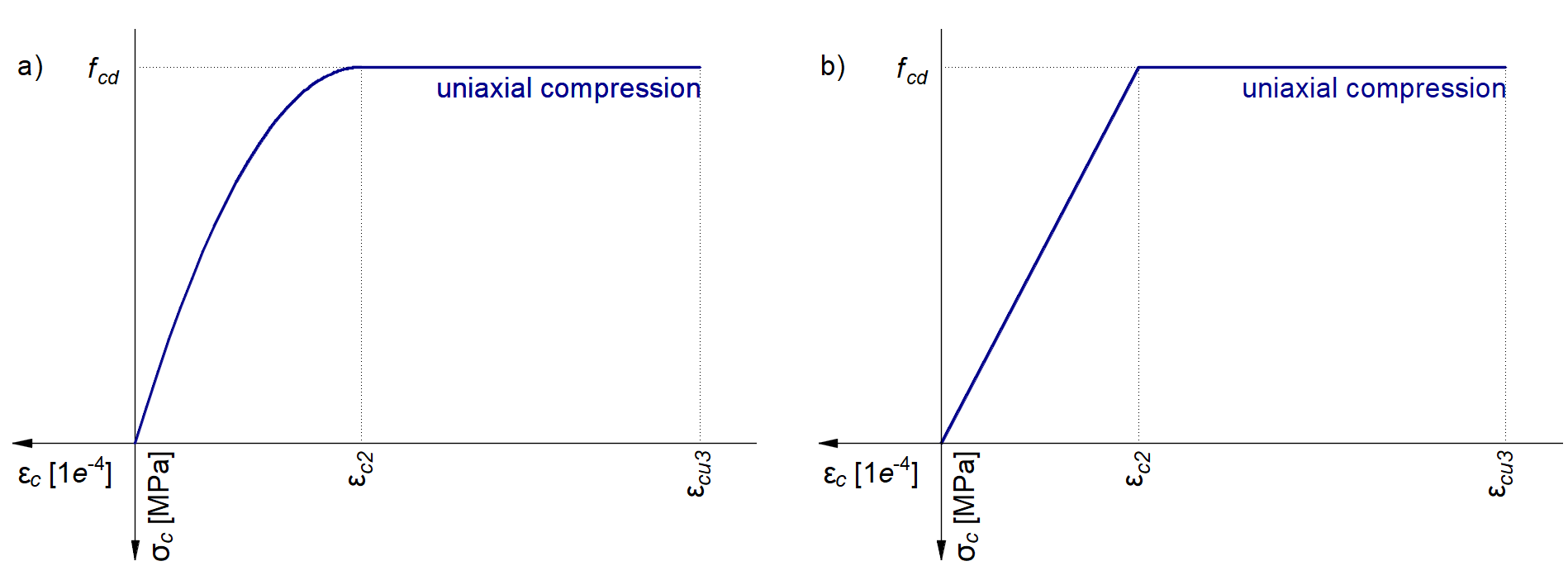
El modelo de hormigón implementado en 3D CSFM se basa en las leyes constitutivas de compresión uniaxial prescritas por EN 1992-1-1 para el cálculo de secciones transversales, que sólo dependen de la resistencia a la compresión. El diagrama parábola-rectángulo especificado en EN 1992-1-1 Cl. 3.1.7 (1) (Fig. 15a) se utiliza por defecto en 3D CSFM, pero los diseñadores también pueden elegir una relación plástica ideal elástica más simplificada de acuerdo con EN 1992-1-1 Cl. 3.1.7 (2) (Fig. 15b). La resistencia a la tracción se desprecia, como en el diseño clásico de hormigón armado.

\[ \textsf{\textit{footnotesize{Fig 15\qquad Diagramas tensión-deformación del hormigón para ULS: a) diagrama parábola-rectángulo; b) diagrama bilineal}}}]

La implementación de CSFM 3D en IDEA StatiCa Detail no considera un criterio de fallo explícito en términos de deformaciones para el hormigón en compresión (es decir, después de alcanzar la tensión máxima, considera una rama plástica con _εcu2 (_εcu3) en un valor del 5% mientras que EN 1992-1-1 asume una deformación última inferior al 0,35%). Esta simplificación no permite verificar la capacidad de deformación de las estructuras que fallan en compresión. Sin embargo, su capacidad última _fcd según EN 1992-1-1 3.1.3 se predice correctamente cuando el aumento de la fragilidad del hormigón a medida que aumenta su resistencia se considera mediante el factor de reducción \ (\eta_{fc}\) definido en el Código Modelo fib 2010 de la siguiente manera:

\[f_{cd}={\alpha_{cc}} \cdot \frac{f_{ck,red}}{γ_c} = {\alpha_{cc}} \...frac... feta...fc... \f_{ck}{γ_c}]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{ck}}}}} \right)^{\frac{1}{3}} \le 1\]

donde:

_αcc es el coeficiente que tiene en cuenta los efectos a largo plazo sobre la resistencia a la compresión y los efectos desfavorables derivados de la forma de aplicar la carga. Es conforme a la norma EN 1992-1-1 Cl. 3.1.6 (1). El valor por defecto es 1,0.

_fck es la resistencia característica del cilindro de hormigón (en MPa para la definición de \ ( \eta_{fc} \)).

Refuerzo

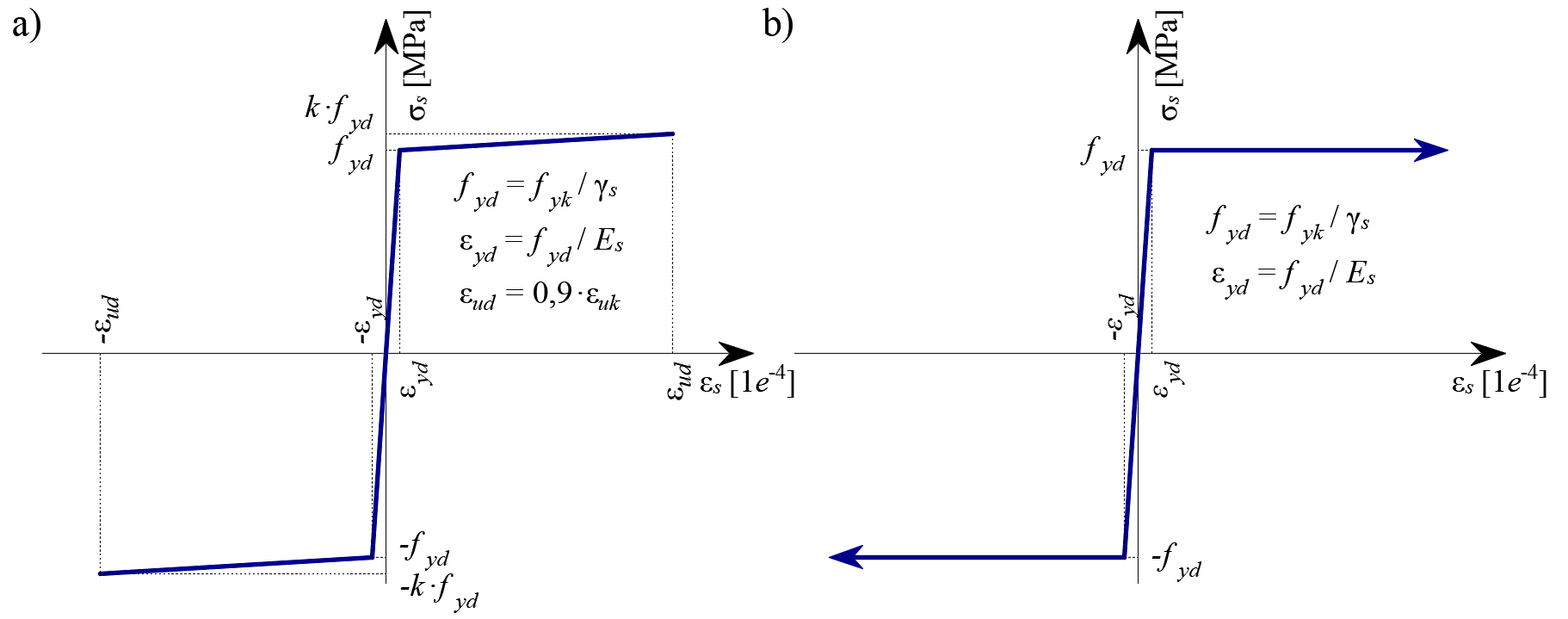
Por defecto, se considera el diagrama tensión-deformación bilineal idealizado para las armaduras desnudas definido en EN 1992-1-1, sección 3.2.7 (Fig. 16). La definición de este diagrama sólo requiere conocer las propiedades básicas de la armadura durante la fase de diseño (clase de resistencia y ductilidad). Siempre que se conozcan, se puede considerar la relación tensión-deformación real de la armadura (laminada en caliente, trabajada en frío, templada y autotemplada, ...). El diagrama tensión-deformación de la armadura puede ser definido por el usuario, pero en este caso es imposible asumir el efecto de rigidización por tracción (es imposible calcular la anchura de la fisura). La utilización del diagrama tensión-deformación con una rama superior horizontal no permite verificar la durabilidad estructural. Por lo tanto, es necesaria la verificación manual de los requisitos de ductilidad estándar.

\[ \textsf{\textit{footnotesize{Fig. 16 \qquad Diagrama tensión-deformación de la armadura: a) diagrama bilineal con una rama superior inclinada; b) diagrama bilineal}}]. \con una rama superior horizontal.

La rigidización por tracción (Fig. 17) se tiene en cuenta automáticamente modificando la relación tensión-deformación de entrada de la barra de refuerzo desnuda para capturar la rigidez media de las barras embebidas en el hormigón (_εm).

\[ \textsf{\textit{footnotesize{Fig. 17\qquad Esquema de rigidización a tracción.}}]

Partial safety factors

The Compatible Stress Field Method is compliant with modern design codes. As the calculation models only use standard material properties, the partial safety factor format prescribed in the design codes can be applied without any adaptation. In this way, the input loads are factored, and the characteristic material properties are reduced using the respective safety coefficients prescribed in design codes, exactly as in conventional concrete analysis. Values of material safety factors prescribed in EN 1992-1-1 chap. 2.4.2.4 are set by default, but the user can change safety factors in the Code and calculation settings (Fig. 18).

\[ \textsf{\textit{\footnotesize{Fig. 18\qquad The setting of material safety factors in Idea StatiCa Detail.}}}\]

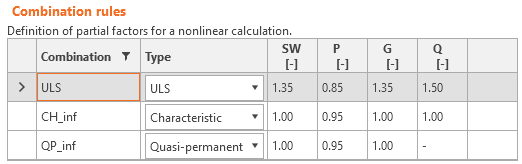
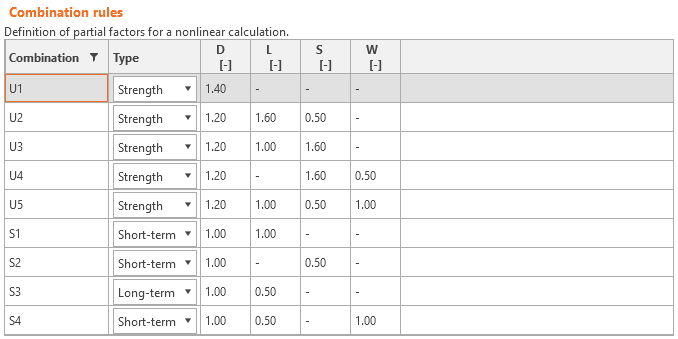
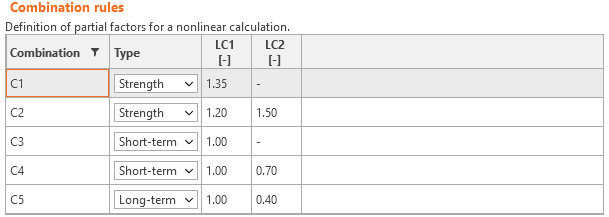
Load safety factors have to be defined by the user in Combination rules for each non-linear combination of load cases (Fig. 19). For all templates implemented in Idea StatiCa Detail, partial safety factors are already predefined.

\[ \textsf{\textit{\footnotesize{Fig. 19\qquad The setting of load partial factors in Idea StatiCa Detail.}}}\]

By using appropriate user-defined combinations of partial safety factors, users can also compute with 3D CSFM using the global resistance factor method (Navrátil, et al. 2017), but this approach is hardly ever used in design practice. Some guidelines recommend using the global resistance factor method for non-linear analysis. However, in simplified non-linear analyses (such as 3D CSFM), which only require those material properties that are used in conventional hand calculations, it is still more desirable to use the partial safety format.

Comprobaciones del estado límite final

Las diferentes verificaciones exigidas por la norma EN 1992-1-1 se evalúan a partir de los resultados directos proporcionados por el modelo. Las verificaciones ULS se llevan a cabo para la resistencia del hormigón, la resistencia de la armadura y el anclaje (esfuerzos cortantes de adherencia).

La resistencia del hormigón en compresión se evalúa como la relación entre la tensión principal equivalente máxima σc_,eqobtenida del análisis de EF y el valor límite σc_,lim = _fcd.

La tensión principal equivalente expresa la tensión uniaxial equivalente para un estado de tensión triaxial general.

\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]

El valor σc_,eq puede, por tanto, compararse directamente con los límites de resistencia uniaxial según 1992-1-1 Cl. 3.1.7 (1).

Esta expresión se deriva de la aplicación de la teoría de la plasticidad de Mohr-Coulomb, suponiendo de forma conservadora el ángulo de rozamiento interno φ = 0°.

La resistencia de la armadura se evalúa tanto en tracción como en compresión como la relación entre la tensión en la armadura en las fisuras _σsr y el valor límite especificado σs_,lim:

\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}{qquad\qquad\textsf{\small{para diagrama bilineal con rama superior inclinada}})

\(σ_{s,lim} = \frac{f_{yk}{γ_s}qquad\qquad\textsf{\small{para diagrama bilineal con rama superior horizontal})

donde:

_fyk es el límite elástico de la armadura según EN 1992-1-1 Cl. 3.2.3,

k es la relación entre la resistencia a la tracción_ftk y el límite elástico,
\(k = \frac{f_{tk}}{f_{yk}})

γs_esel factor de seguridad parcial de la armadura.

El esfuerzo cortante de adherencia se evalúa independientemente como la relación entre el esfuerzo de adherencia _τb calculado mediante el análisis de EF y la resistencia última de adherencia _fbd_, de acuerdo con la norma EN 1992-1-1 cap. 8.4.2: "Esfuerzos de adherencia". 8.4.2:

\[\frac{τ_{b}}{f_{bd}}le 1\].

\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]

donde:

_fctdes el valor de cálculo de la resistencia a tracción del hormigón según EN 1992-1-1 Cl. 3.1.6 (2). Debido a la creciente fragilidad del hormigón de mayor resistencia, fctk_,0.05se limita al valor para C60/75 según EN 1992-1-1 Cl. 8.4.2 (2)

_η1 es un coeficiente relacionado con la calidad del estado de adherencia y la posición de la barra durante el hormigonado (Fig. 31).

_η1 = 1,0 cuando se obtienen condiciones "buenas" y

_η1 = 0,7 para todos los demás casos y para barras en elementos estructurales construidos con encofrados deslizantes, a menos que pueda demostrarse que existen "buenas" condiciones de adherencia

_η2 está relacionado con el diámetro de la barra:

_η2 = 1,0 para Ø ≤ 32 mm

_η2 = (132 - Ø)/100 para Ø > 32 mm

\[ \textsf{\textit{\footnotesize{Fig. 20\qquad EN 1992-1-1 Figura 8.2 - Descripción de las condiciones de adherencia.}}]

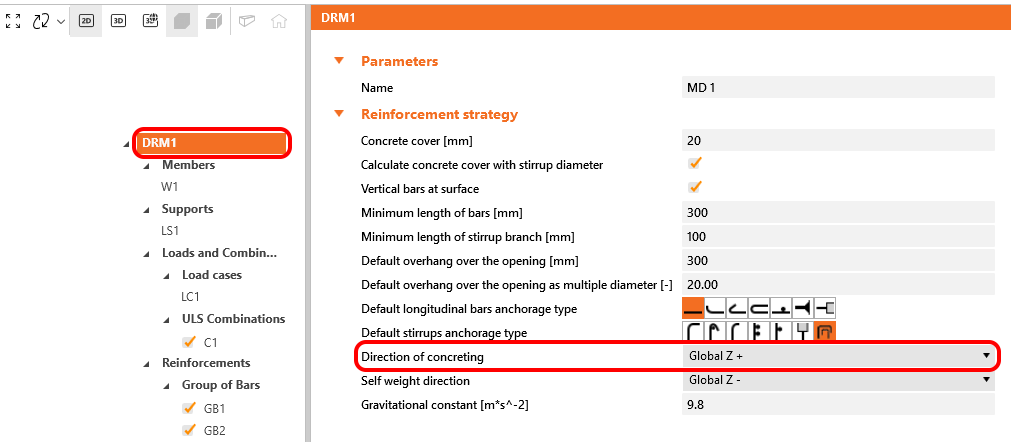
En IDEA StatiCa Detail, las condiciones de adherencia se tienen en cuenta según la Fig. 20 c) y d). La dirección del hormigonado puede establecerse en la aplicación para cada elemento del proyecto de la siguiente manera:

\[ \textsf{\textit{footnotesize{Fig. 21\qquadirección del hormigonado}}]

Estas comprobaciones se realizan con respecto a los valores límite apropiados para las respectivas partes de la estructura (es decir, a pesar de tener una única calidad tanto para el hormigón como para el material de la armadura, los diagramas tensión-deformación finales diferirán en cada parte de la estructura debido a los efectos de rigidización por tracción y ablandamiento por compresión).

Fuerza total _Ftot y fuerza límite _Flim

La fuerza total _Ftot es el resultado del análisis de elementos finitos y puede definirse de dos maneras.

\[F_{tot}=A_{s}\cdot \sigma_{s}\]

donde_As es el área de la barra de refuerzo y _σs es la tensión en la barra.

O como suma de la fuerza de anclaje_{Fa y}la fuerza de adherencia _Fbond.

\[F_{tot}=F_{a}+F_{bond}\]

donde_Fa es la fuerza real en el muelle de anclaje y _Fbond es la fuerza de adherencia que puede obtenerse integrando la tensión de adherencia _τb a lo largo de la longitud de la barra de armadura l.

\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]

_Cs es la circunferencia de la barra de refuerzo.

La fuerza límite_Flim es la fuerza máxima en el elemento de la barra de refuerzo teniendo en cuenta la resistencia última de la barra de refuerzo y también las condiciones de anclaje (unión entre el hormigón y la armadura y ganchos de anclaje, bucles, etc.).

\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]

\[F_{u}=k\cdot f_{yd}\cdot A_{s}]

\F_{au}=beta k\cdot f_{yd}\cdot A_{s}]

\F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\cdot A_{s}]

donde _Cs es la circunferencia de la barra de refuerzo, y l es la longitud desde el comienzo de la barra de refuerzo hasta el punto de interés.

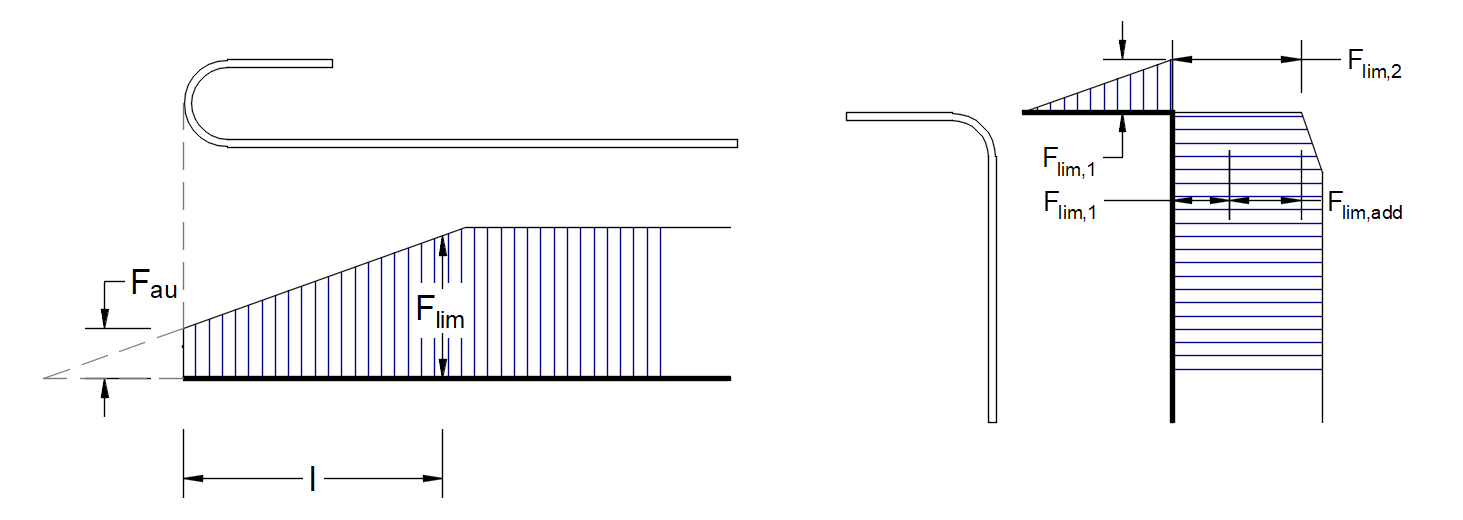
\[ \textsf{\textit{footnotesize{Fig. 22\qquad Definición de la fuerza límite Flim}}}]

\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]

donde_Flim,add es la fuerza adicional calculada a partir de la magnitud del ángulo entre elementos vecinos._Flim,2 debe ser siempre inferior a_Fu.

Los tipos de anclaje disponibles en 3D CSFM incluyen una barra recta (es decir, sin reducción del extremo del anclaje), curva, gancho, bucle, barra transversal soldada, unión perfecta y barra continua. Todos estos tipos, junto con los respectivos coeficientes de anclaje β, se muestran en la Fig. 23 para la armadura longitudinal y en la Fig. 24 para los estribos. Los valores de los coeficientes de anclaje adoptados están de acuerdo con la norma EN 1992-1-1 sección 8.4.4 Tab. 8.2. Cabe señalar que a pesar de las diferentes opciones disponibles, 3D CSFM distingue tres tipos de extremos de anclaje: (i) sin reducción de la longitud de anclaje, (ii) una reducción del 30% de la longitud de anclaje en el caso de un anclaje normalizado, y (iii) unión perfecta.

\[ \textsf{\textit{footnotesize{Fig. 23\qquad Tipos de anclaje disponibles y coeficientes de anclaje respectivos para barras de refuerzo longitudinal en el CSFM 3D:}}}]

\(a) barra recta; (b) curva; (c) gancho; (d) bucle; (e) barra transversal soldada; (f) unión perfecta; (g) barra continua.

\[ \textsf{\textit{footnotesize{Fig. 24\qquad Tipos de anclaje disponibles y coeficientes de anclaje respectivos para estribos.}}]

\Estribos cerrados: (a) gancho; (b) curva; (c) solapamiento. Estribos abiertos: (d) gancho; (e) barra continua.]

Para cumplir con la norma EN 1992-1-1, se debe utilizar el muelle de anclaje en el cálculo, el muelle de anclaje se modifica por el coeficiente β por lo que el usuario debe utilizar uno de los tipos de anclaje disponibles al definir las condiciones de inicio y final de la armadura.

Structural verifications according to ACI 318-19

3D CSFM is in accordance with ACI 318-19, chapter 6.8.1.1. In order for the 3D CSFM to meet the requirements from ACI 318-19 Section 6.8.1.2, a lot of verification testing was done at various universities. Individual articles summarizing the results of verification and validation can be found at the following link.

Verifications: Detail 3D

Modelos de materiales en 3D CSFM (ACI)

Hormigón - Resistencia

El modelo de hormigón implementado para los cálculos de resistencia en el CSFM se basa en la curva de tensión-deformación parabólico-plástica para hormigón basada en la curva de tensión-deformación parabólica de la Asociación de Cemento Portland descrita en las Notas de PCA sobre los Requisitos del Código de Construcción ACI 318-99 para el Hormigón Estructural, Figura 6-8. La resistencia a la tracción se desprecia, al igual que en el diseño clásico de hormigón armado. La resistencia a la tracción se desprecia, como en el diseño clásico del hormigón armado.

\[ \textsf{\textit{footnotesize{Fig. 38\qquad Diagrama tensión-deformación del hormigón para el análisis de resistencia}}]

La implementación del CSFM en IDEA StatiCa Detail no considera un criterio de fallo explícito en términos de deformaciones para el hormigón en compresión (es decir, después de alcanzar la tensión pico considera una rama plástica con _εc0 en valor máximo 5% mientras que ACI 318-19 Cl. 22.2.2.1 asume una deformación última menor que 0.3%). Esta simplificación no permite verificar la capacidad de deformación de las estructuras que fallan en compresión. Sin embargo, la resistencia se predice correctamente cuando el aumento de la fragilidad del hormigón a medida que aumenta su resistencia se considera mediante el factor de reducción \ (\eta_{fc}\) definido en el Código Modelo fib 2010 de la siguiente manera:

\[f'_{c,lim}=\alpha_{1}\cdot\phi_{c}\cdot \eta _{fc}\cdot f'_{c}\].

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f'_{c}}}}} \right)^{\frac{1}{3}} \le 1\]

donde:

_α1 es el factor de reducción de la resistencia a compresión del hormigón definido en ACI 318-19 Cl. 22.2.2.4.1. Cuando se utiliza un diagrama tensión-deformación parábola-rectángulo, es necesario reducir la tensión máxima de compresión por este factor. Esto promedia la distribución de la tensión en la zona de compresión de tal manera que la resistencia a la compresión resultante es menor o igual a la resistencia a la compresión calculada utilizando un diagrama tensión-deformación con una rama plástica decreciente.

Φc_esel factor de reducción de la resistencia del hormigón. El valor por defecto se establece de acuerdo con ACI 318-19 Tabla 24.2.1 (b)(f).

f'_c es la resistencia cilíndrica del hormigón (en MPa para la definición de \ ( \eta_{fc} \)).

Refuerzo

Se considera un diagrama tensión-deformación perfectamente elasto-plástico con un límite elástico definido para la armadura no pretensada. Véase ACI 319-19 CL. 20.2.1. La definición de este diagrama sólo requiere conocer las propiedades básicas de la armadura: resistencia y módulo de elasticidad.

El diagrama tensión-deformación de la armadura también puede ser definido por el usuario, pero en este caso, es imposible asumir el efecto de rigidización por tracción.

\[ \textsf{\textit{footnotesize{Fig. 42 \qquad Diagrama tensión-deformación de la armadura}}]

donde:

Φs_esel factor de reducción de resistencia de la armadura. El valor por defecto se establece de acuerdo con ACI 318-19 Tabla 24.2.1.

_fy es el límite elástico de la armadura

_Es el módulo de elasticidad de la armadura

Se selecciona el 10% como deformación límite en la que se detiene el cálculo. Este valor se considera seguro según el artículo 7 de ASTM A955/A955M-20c.

La rigidez por tracción (Fig. 43) se tiene en cuenta automáticamente modificando la relación tensión-deformación de entrada de la barra de refuerzo desnuda para capturar la rigidez media de las barras embebidas en el hormigón (_εm).

\[ \textsf{\textit{footnotesize{Fig. 43\qquad Esquema de rigidización a tracción.}}]

Strength reduction factors and load factors

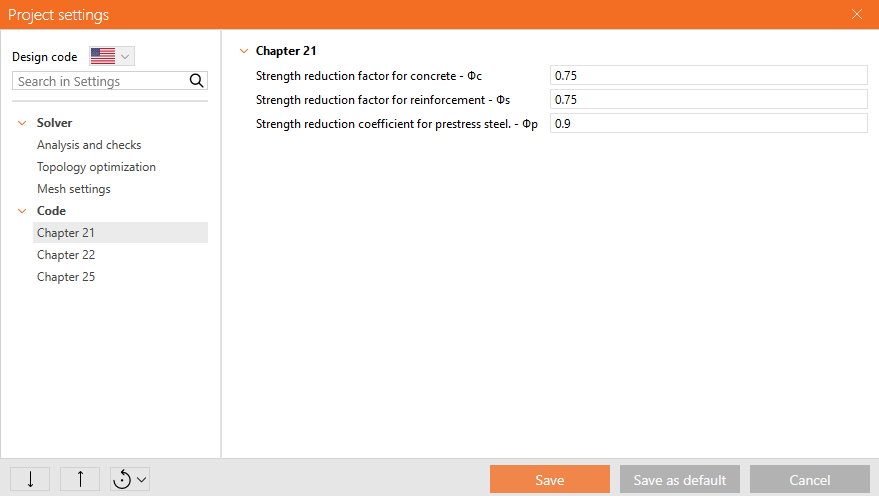
Values of strength reduction factors are prescribed in ACI 318-19 Cl. 21.2. The default values for concrete and reinforcement are chosen based on the assumption that the typical example solved in the application is shear-controlled (based on Table 21.2.1 (b), (f), (g)). However, it is possible to model any type of element. Therefore, if a compression or tension-controlled element is assessed, the user has the option to change the strength reduction factor value in the Preferences.

\[ \textsf{\textit{\footnotesize{Fig. 42\qquad The setting of strength reduction factors in IDEA StatiCa Detail.}}}\]

Load factors for Strength combinations shall be defined according to ACI 318-19 Table 5.3.1.

Except as stated in Chapter 34, service-level load combinations are not defined in ACI 318-19. It is recommended to use combination rules based on Appendix C of ASCE/SEI 7-16. For all templates, load factors are already predefined.

\[ \textsf{\textit{\footnotesize{Fig. 43\qquad The setting of load factors in IDEA StatiCa Detail.}}}\]

Verificaciones de resistencia en Detail 3D

Las distintas verificaciones exigidas por la norma ACI 318-19 se evalúan a partir de los resultados directos proporcionados por el modelo. Las verificaciones se llevan a cabo para la resistencia del hormigón, la resistencia de la armadura y el anclaje (esfuerzos cortantes de adherencia).

La resistencia del hormigón en compresión se evalúa como la relación entre la tensión principal equivalente máxima fc_,eq (también σc_,eq en el texto anterior) obtenida a partir del análisis de EF y el valor límite f'_c,lim.

La tensión principal equivalente expresa la tensión uniaxial equivalente para un estado de tensión triaxial general.

\[f_{c,eq} = \sigma_{c3}} - \sigma_{c1}\].

El valor de fc_, eq puede, por tanto, compararse directamente con los límites de resistencia uniaxial. Esta expresión se deriva de la aplicación de la teoría de la plasticidad de Mohr-Coulomb, asumiendo de forma conservadora el ángulo de fricción interna φ = 0°.

La resistencia de la armadura se evalúa tanto en tracción como en compresión como la relación entre la tensión en la armadura en las fisuras _fs y el valor límite especificado fy_,lim.

\[f_{y,lim} = \phi_{s} \cdot f_{y}\]

El esfuerzo cortante de adherencia se evalúa independientemente como la relación entre el esfuerzo de adherencia _τb calculado mediante el análisis de EF y la resistencia de adherencia _fbu.

Aunque la resistencia de adherencia no se define explícitamente en ACI 318-19, el cálculo de la longitud de desarrollo se puede encontrar en la Sección 25.4.2. Sin embargo, dado que la resistencia de adherencia es el dato básico para determinar la longitud de desarrollo, véase R25.4.1.1 y ACI Comité 408 1966, la resistencia de adherencia puede calcularse como sigue:

Supongamos que si anclamos la barra de armadura en un bloque de hormigón hasta la longitud de desarrollo _ld o mayor, el arrancamiento de la armadura producirá la rotura de la armadura y no el arrancamiento del hormigón. Esto se puede escribir con la siguiente fórmula.

\[\pi\cdot d_{b} \cdot l_{d} \cdot f_{bu}=f_{y}\cdot A_{s}]

donde:

_db es el diámetro de la barra de armadura, _ld es la longitud de desarrollo, _fbu es el límite de adherencia, _fy es el límite elástico de la armadura y_As es el área de la barra de armadura.

De lo anterior se deduce fácilmente la fórmula para calcular la fuerza de adherencia:

\f_{bu}=frac{f_{y}\cdot A_{s}}{pi\cdot d_{b} \cdot l_{d} }].

La longitud de desarrollo _ld se determina entonces de acuerdo con ACI 318-19 Tabla 25.4.2.3 de la siguiente manera:

\[l_{d}=\left( \frac{f_{y}\cdot\psi_{t}\cdot\psi_{e}\cdot\psi_{g}}{C\cdot\lambda\sqrt{f'_{c}}} \d_{b}]

donde:

C = 25 (2,1 para métrica) para no. 6 y barras más pequeñas y alambres deformados, C = 20 (1,7 para el sistema métrico) para no. 7 y barras mayores, λ = 1,0 para hormigón de peso normal, _ψt, _ψe_, _ψg se determinan de acuerdo con ACI 318-19 Tabla 25.4.2.3.

Sólo se soportan las armaduras no revestidas o revestidas de zinc (galvanizadas), por lo que _ψe = 1,0. _ψg se determina automáticamente a partir del grado de la armadura, y _ψt se deriva automáticamente de la posición de la armadura en el modelo y de la dirección de hormigonado que puede establecerse en la aplicación para cada elemento del proyecto de la siguiente manera.

\[ \textsf{\textit{footnotesize{Fig. 46\qquadirección del hormigonado}}}]

Fuerza total _Ftot y fuerza límite _Flim

La fuerza total _Ftot es el resultado del análisis de elementos finitos y puede definirse de dos maneras.

\[F_{tot}=A_{s} \cdot f_{s}\]

donde_As es el área de la barra de refuerzo y _fs es la tensión en la barra.

O como suma de la fuerza de anclaje_{Fa y}la fuerza de adherencia _Fbond.

\[F_{tot}=F_{a}+F_{bond}\]

\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]

_Cs es la circunferencia de la barra de refuerzo.

La fuerza límite_Flim es la fuerza máxima en el elemento de la barra de refuerzo teniendo en cuenta la resistencia de la barra de refuerzo y también las condiciones de anclaje (unión entre el hormigón y la armadura y ganchos de anclaje, bucles, etc.).

\[F_{lim}=min_left( F_{lim,bond}+F_{au},F_{u} \right)\}]

\[F_{u}=f_{y,lim}\cdot A_{s}]

\F_{au}=f_{y,lim}dot A_{s}]

\F_{lim,bond}=C_{s}{cdot l}{cdot f_{bu}{]

donde _Cs es la circunferencia de la barra de refuerzo, y l es la longitud desde el comienzo de la barra de refuerzo hasta el punto de interés.

\[ \textsf{\textit{footnotesize{Fig. 47\qquad Definición de la fuerza límite Flim}}]

\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]

donde_Flim,add es la fuerza adicional calculada a partir de la magnitud del ángulo entre elementos vecinos._Flim,2 debe ser siempre inferior a_Fu.

Los tipos de anclaje disponibles en CSFM incluyen una barra recta (es decir, sin reducción del extremo del anclaje), gancho de 90 grados, gancho de 180 grados, unión perfecta y barra continua. Todos estos tipos, junto con los respectivos coeficientes de anclaje β, se muestran en la Fig. 48 para la armadura longitudinal. Los valores de los coeficientes de anclaje adoptados se derivan de la comparación de la ecuación de la sección ACI 318-19 25.4.3.1 y ecuaciones tomadas de la sección ACI 318-19 25.4.2.3. Cabe señalar que, a pesar de las diferentes opciones disponibles, el CSFM distingue tres tipos de extremos de anclaje: (i) ninguna reducción de la longitud de anclaje, (ii) una reducción del 30% de la longitud de anclaje en el caso de un anclaje normalizado, y (iii) unión perfecta.

\[ \textsf{\textit{footnotesize{Fig. 48\qquad Tipos de anclaje disponibles y coeficientes de anclaje respectivos para barras de refuerzo longitudinal en CSFM:}}]

\(a) barra recta; (b) gancho de 90 grados; (c) gancho de 180 grados; (d) unión perfecta; (e) barra continua}}].

El coeficiente de anclaje de los estribos es siempre - β = 1,0.

Para cumplir con ACI, el resorte de anclaje debe ser utilizado en el cálculo, el resorte de anclaje es modificado por el coeficiente β por lo que el usuario debe utilizar uno de los tipos de anclaje disponibles al definir las condiciones de inicio y final de la armadura.

Structural verifications according to Australian standard AS 3600

The CSFM is a structural analysis method that satisfies the general rules in Chapters 6.1.1 and 6.1.2 and is defined as (f) non-linear stress analysis in Chapter 6.1.3 - further in Chapter 6.6.

In order to satisfy the requirements in Sections 6.6.4 and 6.6.5 - more can be found in AS3600:2018 Sup 1:2022 Section C6.6 - verification and validations of the method were done. Individual articles summarizing the results of verification and validation can be found at the following link.

Verifications: Detail 3D

Since IDEA StatiCa Detail is a practical design program, factored characteristic compressive cylinder strength at 28 days f'c is used for calculations, as is described in the next chapter.

Material models in 3D CSFM (AS 3600)

Concrete - Strength

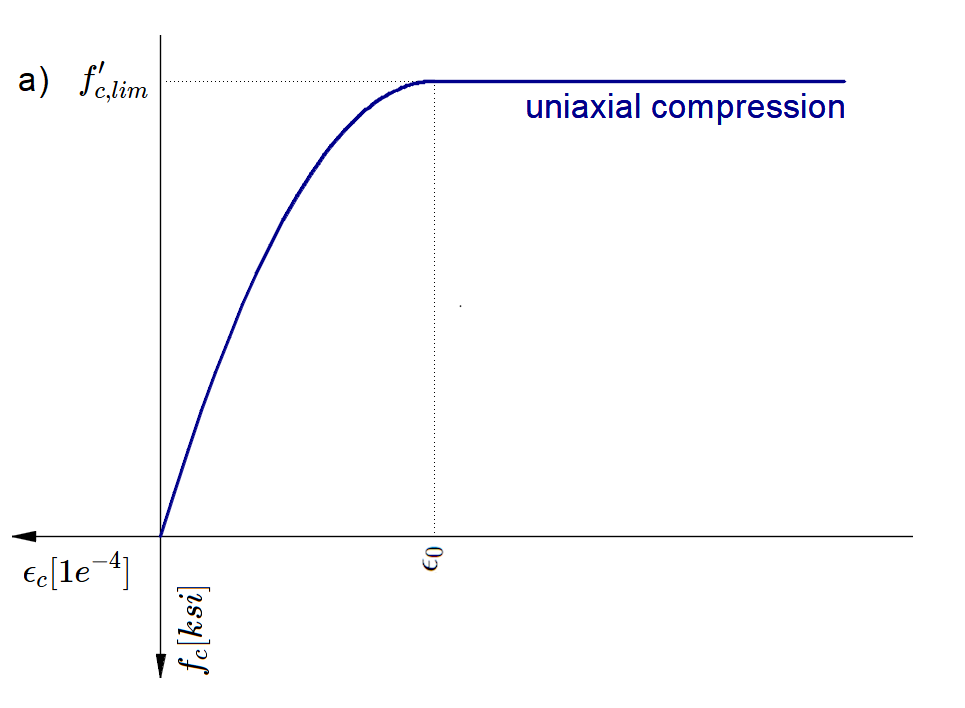
The concrete model implemented for strength calculations in CSFM is based on the parabolic-plastic stress-strain curve. The tensile strength is neglected, as it is in classic reinforced concrete design.

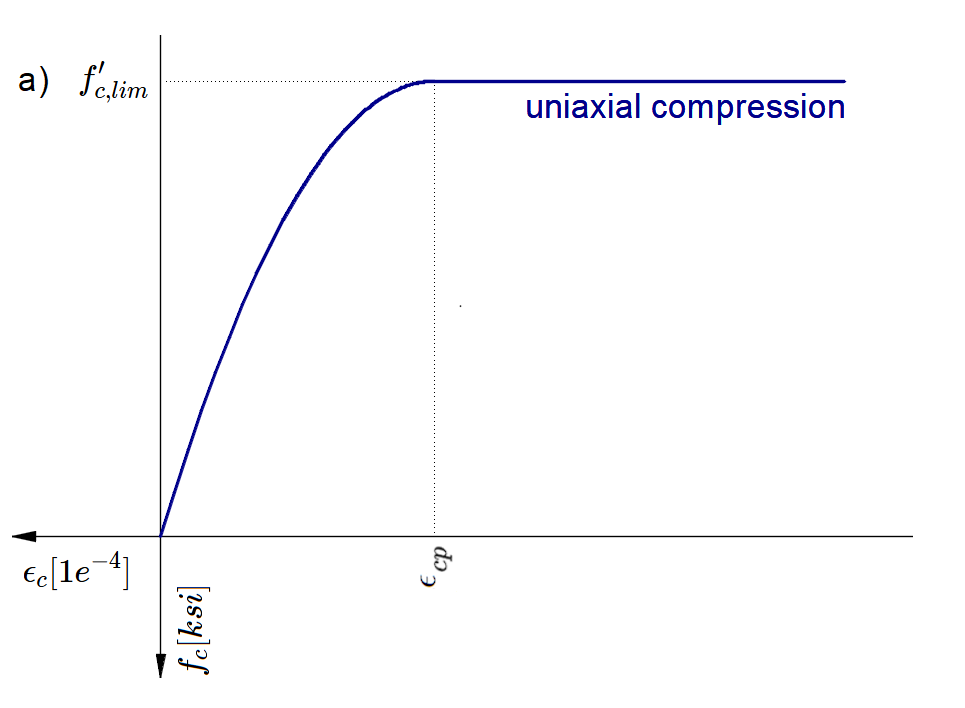
\[ \textsf{\textit{\footnotesize{Fig. 47\qquad The stress-strain diagram of concrete for Strength analysis}}}\]

The implementation of CSFM in IDEA StatiCa Detail does not consider an explicit failure criterion in terms of strains for concrete in compression (i.e., after the peak stress is reached, it considers a plastic branch with ε_cp in maximum value 5%, while AS 3600 Cl. 8.3.1 assumes ultimate strain of less than 0.3%). This simplification does not allow the deformation capacity of structures failing in compression to be verified. However, the strength is properly predicted when the increase in the brittleness of concrete as its strength rises is considered by means of the \(\eta_{fc}\) reduction factor defined in fib Model Code 2010 as follows:

\[f'_{c,lim}=\alpha_{2}\cdot\phi_{s} \cdot \eta_{fc}\cdot f'_{c}\]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f'_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]

where:

α₂ is the reduction factor of concrete compressive strength defined in AS 3600 Cl. 8.3.1
When using a parabola-rectangle stress-strain diagram, it is necessary to reduce the maximum compressive stress by this factor. This averages the stress distribution in the compression zone in such a way that the resulting compressive strength is less than or equal to the compressive strength calculated using a stress-strain diagram with a decreasing plastic branch. An analogous approach is defined for the Rectangular stress block in Chapter 8.1.3.

Φ_sis the stress reduction factor for concrete. The default value is set according to AS 3600 Table 2.2.3.

f'_c is the concrete cylinder strength (in MPa for the definition of \( \eta_{fc} \)).

Reinforcement

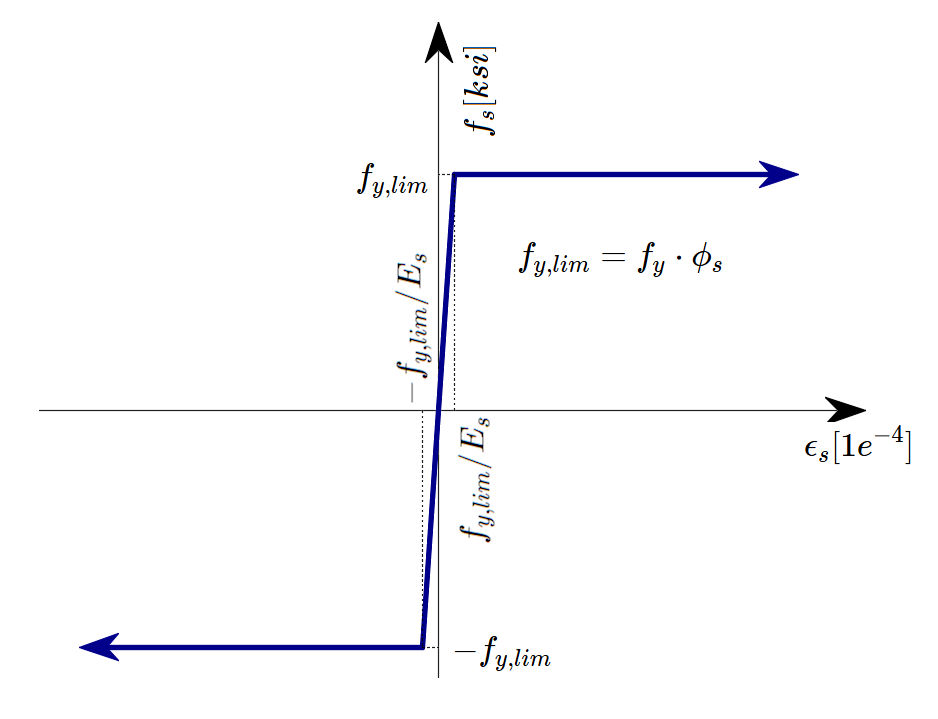
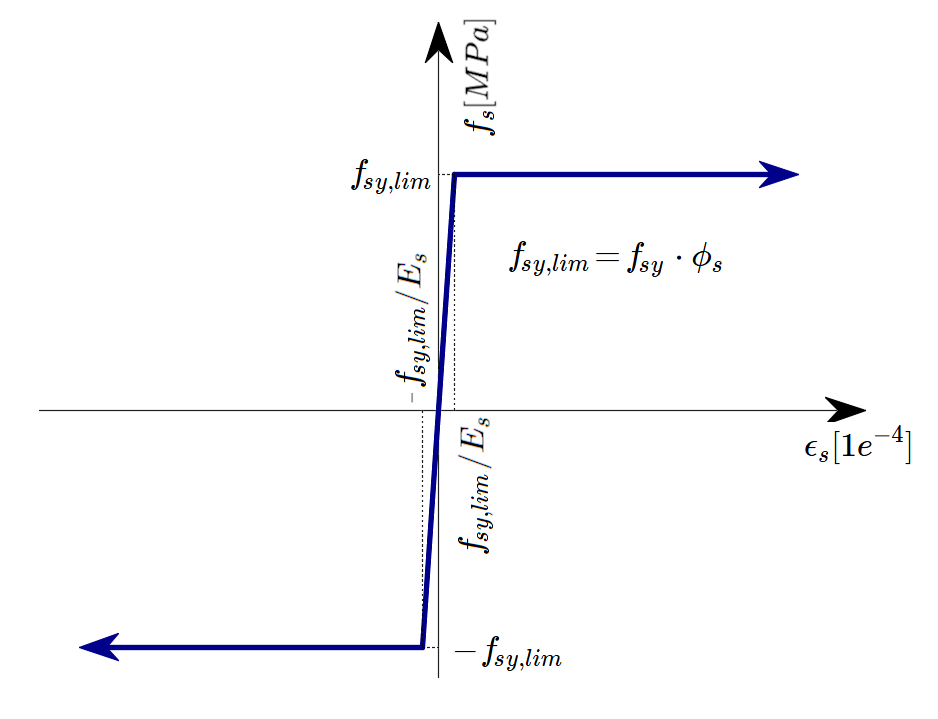
A perfectly elasto-plastic stress-strain diagram with a defined yield point for the non-prestresses reinforcement is considered, see AS 3600 Section 3.2. The definition of this diagram only requires the basic properties of the reinforcement to be known – the strength and modulus of elasticity.

The reinforcement stress-strain diagram can be also defined by the user, but in this case, it is impossible to assume the tension stiffening effect (it is impossible to calculate crack width).

\[ \textsf{\textit{\footnotesize{Fig. 48 \qquad Stress-strain diagram of reinforcement}}}\]

where:

Φ_sis the strength reduction factor for reinforcement. Where the default value is set according to AS 3600 Table 2.2.3.

f_y is the yield strength of reinforcement

E_s modulus of elasticity of reinforcement

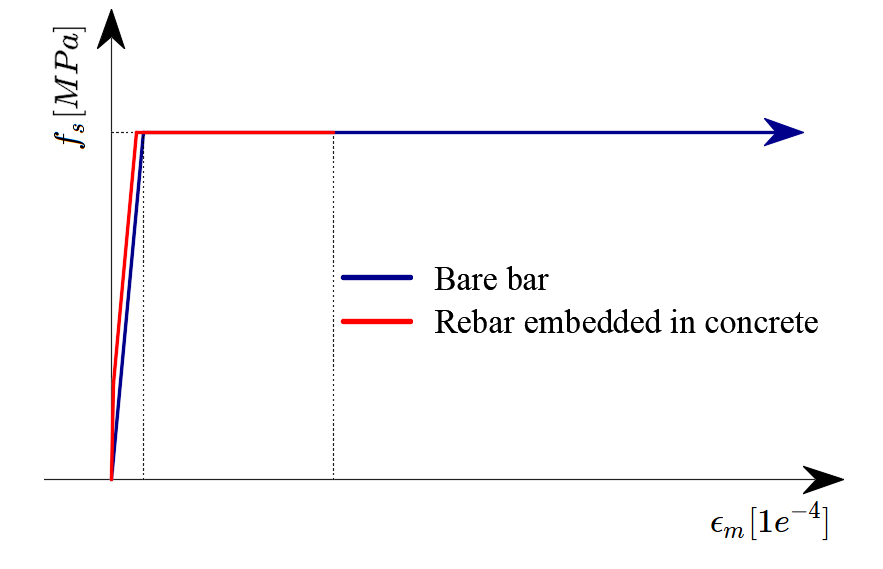
Tension stiffening (Fig. 49) is accounted for automatically by modifying the input stress-strain relationship of the bare reinforcing bar in order to capture the average stiffness of the bars embedded in the concrete (ε_m).

\[ \textsf{\textit{\footnotesize{Fig. 49\qquad Scheme of tension stiffening.}}}\]

Stress and strength reduction factors and load factors

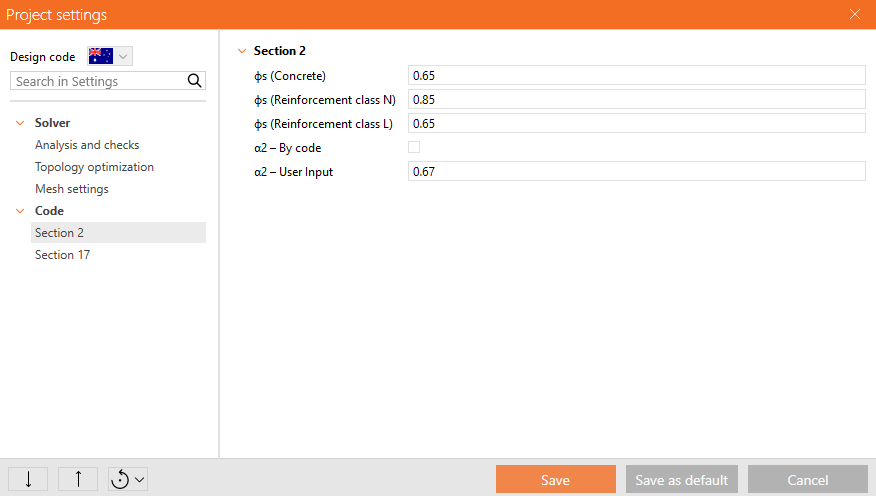
Values of stress reduction factors are prescribed in AUS 3600 Cl. 2.2.3. The default values for concrete and reinforcement are set according to Table 2.2.3

\[ \textsf{\textit{\footnotesize{Fig. 50\qquad The setting of stress reduction factors in IDEA StatiCa Detail.}}}\]

Load factors for Strength combinations shall be defined according to AS 3600 Cl. 4.2.2. Load factors for Serviceability combinations shall be determined according to Table 4.1. For all templates, load factors are already predefined.

\[ \textsf{\textit{\footnotesize{Fig. 51\qquad The setting of load factors in Idea StatiCa Detail.}}}\]

Strength and anchorage verifications in Detail 3D

The different verifications required by AS 3600 are assessed based on the direct results provided by the model. Verifications are carried out for concrete strength, reinforcement strength, and anchorage (bond shear stresses).

Strength - Concrete

The concrete strength in compression is evaluated as the ratio between the maximum Equivalent principal stress f_c,eq (also σ_c,eq in previous text) obtained from FE analysis and the limit value f'_c,lim.

Equivalent Principal Stress expresses the equivalent uni-axial stress for a general tri-axial stress state.

\[f_{c,eq} = \sigma_{c3} - \sigma_{c1}\]

The f_c,eq value can, therefore, be directly compared with uniaxial strength limits. This expression is derived from the implementation of the Mohr-Coulomb plasticity theory, conservatively assuming the angle of internal friction φ = 0°.

Strength - Reinforcement

The strength of the reinforcement is evaluated in both tension and compression as the ratio between the stress in the reinforcement at the cracks f_s and the specified limit value f_sy,lim.

\[f_{sy,lim} = \phi_{s} \cdot f_{sy}\]

Strength - Anchors

Anchors are checked for normal stresses in a similar way to reinforcement, where the limit value f_sy,lim is determined.

In the current version, the code checks for anchors in shear and shear with tension are not available.

Pull-out check for headed anchors (Washer plates and Headed studs)

For headed anchors, an additional stop criterion is implemented to check the concrete bearing (crushing) above the anchor head - pull-out. During the analysis, the compressive force transferred through the head-to-concrete contact is monitored and compared with the limit value given by AS 5216:2021 Cl. 6.3.4 (pull-out failure of headed fastenings).

\[N_{Rd,p} = \Phi_{Mp} \cdot k_{2} \cdot A_{h} \cdot f'_{c}\]

where:

\( \Phi_{Mp}\) is the strength reduction factor - Table 3.2.4
A_h is the load bearing area of the head of the fastener (without the shank area).
f_c' is the specified compressive strength of concrete
k₂ is always taken as 7.5, i.e. the value for cracked concrete. This is consistent with the CSFM approach used in Detail, where the tensile strength of concrete is neglected and the concrete is assumed to be cracked in tension.

Once the contact force reaches this code-based limit, the stop criterion is triggered and the analysis is terminated before the design pull-out resistance is exceeded.

Anchorage - Bond stress

The bond shear stress is evaluated independently as the ratio between the bond stress τ_b calculated by FE analysis and the design ultimate bond stress f_bu.

For the determination of the design ultimate bond stress f_bu, the formula C13.1.2.2 defined in AS3600:2018 Sup 1:2022 is considered in the application.

\[f_{bu}=\frac{k_{2}}{k_{1} \cdot k_{3}} \cdot (0.5 \cdot \sqrt{f'_{c}})\]

Where f'_c ≤ 65 MPa (in the formula is in MPa), and k factors are determined from AS 3600 Cl. 13.1.2.2 as follows:

k₃ = 0.7 (conservative value for all reinforcement)
k₂ = (132 - d_b) / 100 (d_b is diameret of rebar in millimeters)
= 1.3 for a horizontal bar with more than 300 mm of concrete cast below the bar, or 1.0 otherwise

k₁ is automatically derived from the position of the reinforcement in the model and from the direction of concreting that can be set in the application for each project item as follows.

\[ \textsf{\textit{\footnotesize{Fig. 52\qquad Direction of concreting}}}\]

The basic development length L_sy,tb is calculated according to formula 13.1.2.2 in AS 3600 as follows:

\[L_{sy,tb}=\frac{0.5\cdot k_{1}\cdot k_{3}\cdot f_{sy}\cdot d_{b}}{k_{2}\cdot \sqrt{f'_{c}}}\ge 29 \cdot k_{1}\cdot d_{b}\]

As can be seen in the formula, the basic development length L_sy,tb is limited from below, and therefore the design ultimate bond stress f_bu must be limited in the same way in the application, so the following applies:

\[f_{bu}\le \frac{f_{sy}}{116 \cdot k_{1}} \]

Where f_sy is in MPa.

The derivation of the f_bu limitation is as follows:

\[f_{bu}= \frac{f_{sy}\cdot A_{s}}{ \pi \cdot d_{b} \cdot L_{sy,tb}}=\frac{f_{sy}\cdot \pi \cdot d_{b}^{2}}{4 \cdot \pi \cdot d_{b} \cdot 29 \cdot k{1} \cdot d_{b}} =\frac{f_{sy}}{116 \cdot k_{1}} \]

Total force F_tot and limit force F_lim

The total force F_tot is a result of the finite element analysis and can be defined in two ways.

\[F_{tot}=A_{s} \cdot f_{s}\]

where A_s is the area of the reinforcement bar and f_s is the stress in the bar.

Or as a sum of the anchorage force F_aand the bond force F_bond.

\[F_{tot}=F_{a}+F_{bond}\]

where F_a is the actual force in the anchorage spring and F_bond is the bond force that can be obtained by integrating the bond stress τ_b along the length of reinforcement bar l.

\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]

C_s is the circumference of the reinforcement bar.

The limit force F_lim is the maximum force in the element of the rebar considering the strength of the rebar and also anchoring conditions (bond between concrete and reinforcement and anchorage hooks, loops, etc.).

\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]

\[F_{u}=f_{y,lim}\cdot A_{s}\]

\[F_{au}=\beta\cdot f_{y,lim}\cdot A_{s}\]

\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bu}\]

where C_s is the circumference of the reinforcement bar, and l is the length from the beginning of the rebar to the point of interest.

\[ \textsf{\textit{\footnotesize{Fig. 53\qquad Definition of the limit force Flim}}}\]

\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]

where F_lim,add is the additional force calculated from the magnitude of the angle between neighboring elements. F_lim,2 must always be lower than F_u.

The available anchorage types in CSFM include a straight bar (i.e., no anchor end reduction), Standard cog, Standard hook, perfect bond, and continuous bar. All these types, along with the respective anchorage coefficients β, are shown in Fig. 54 for longitudinal reinforcement. The values of the adopted anchorage coefficients are derived from AS 3600 Cl. 13.1.2. It should be noted that CSFM distinguishes three types of anchorage ends: (i) no reduction in the anchorage length, (ii) a reduction of 50% of the anchorage length in the case of a normalized anchorage, and (iii) perfect bond.

\[ \textsf{\textit{\footnotesize{Fig. 54\qquad Available anchorage types and respective anchorage coefficients for longitudinal reinforcing bars in CSFM:}}}\]

\[ \textsf{\textit{\footnotesize{(a) straight bar; (b) Standard cog; (c) Standard hook; (d) perfect bond; (e) continuous bar}}}\]

The anchorage coefficient for stirrups is always - β = 1.0.

In order to comply with AS 3600, the anchorage spring should be used in the calculation. The anchorage spring is modified by the β coefficient, so the user must use one of the available anchorage types when defining the reinforcement start and end conditions.

Prueba hoy mismo la última versión de IDEA StatiCa

Prueba gratis IDEA StatiCa

Verifications and validations

Verifications: Detail 3D

References

Wu, D.; Wang, Y.; Qiu, Y.; Zhang, J.; Wan, Y.-K. Determination of Mohr–Coulomb Parameters from Nonlinear Strength Criteria for 3D Slopes. Math. Probl. Eng. 2019, 6927654.
Lelovic, S.; Vasovic, D.; Stojic, D. Determination of the Mohr-Coulomb Material Parameters for Concrete under Indirect Tensile Test. Tech. Gaz. 2019, 26, 412–419.
Galic, M.; Marovic, P.; Nikolic, Ž. Modified Mohr-Coulomb—Rankine material model for concrete. Eng. Comput. 2011, 28, 853–887.
Fan, Q.; Gu, S.C.; Wang, B.N.; Huang, R.B. Two Parameter Parabolic Mohr Strength Criterion Applied to Analyze The Results of the Brazilian Test. Appl. Mech. Mater. 2014, 624, 630–634.

IDEA StatiCa Detail – Structural design of concrete 3D discontinuities

Navigation

Structural design of concrete 3D discontinuities in IDEA StatiCa Detail

Introduction to the 3D CSFM method