Tensión triaxial: el efecto de confinamiento activo
Introducción
El efecto de confinamiento en estructuras de hormigón se refiere al fenómeno en el que la resistencia y la ductilidad del hormigón mejoran significativamente debido a la presión lateral (activa) o al confinamiento proporcionado por los materiales circundantes (pasiva), como la armadura de acero o las camisas externas. Este efecto es especialmente importante para mejorar el comportamiento del hormigón en compresión, sobre todo bajo cargas elevadas.
He aquí los aspectos clave del efecto de confinamiento en las estructuras de hormigón:
- Aumento de la resistencia: El confinamiento aumenta la resistencia a la compresión del hormigón. Cuando se aplica presión lateral, se frena la expansión lateral del hormigón, lo que le permite soportar mayores cargas axiales antes de fallar.
- Mayor ductilidad: El hormigón confinado presenta una mayor ductilidad, lo que significa que puede sufrir mayores deformaciones antes de fallar.
- Comportamiento bajo carga: El confinamiento modifica el modo de fallo del hormigón, que pasa de ser frágil y repentino a ser más dúctil y gradual. Este cambio en el modo de fallo es beneficioso para la seguridad e integridad de las estructuras en condiciones de carga extremas.
- Consideraciones de diseño: El diseño de elementos de hormigón confinado implica calcular la cantidad y disposición de la armadura de confinamiento para conseguir la resistencia y ductilidad deseadas. Las normas y códigos, como las directrices EN (Eurocódigo), proporcionan fórmulas y directrices para el diseño de elementos de hormigón confinado.
- Aplicaciones: El confinamiento activo se tiene en cuenta a la hora de diseñar, por ejemplo, zonas parcialmente cargadas, bisagras de hormigón, etc.
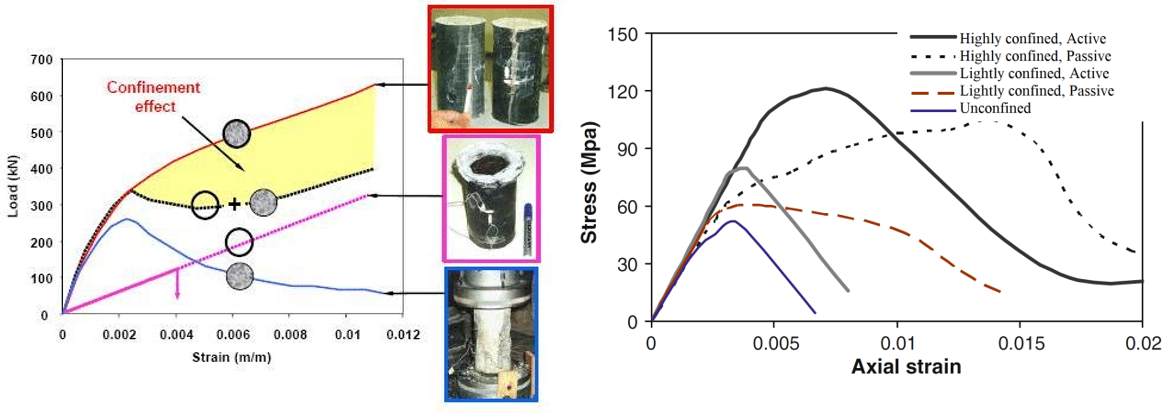
En la siguiente figura se puede observar cómo el diagrama tensión-deformación y la capacidad portante pueden diferir para el hormigón no confinado y el confinado.
\[ \textsf{\textit{footnotesize{Fig. 1\qquad Efecto del confinamiento e influencia en la capacidad portante de las estructuras}}]
Antes de entrar en el ejemplo en sí, recordemos cómo se define el material de hormigón en la aplicación.
Definición del material de hormigón en IDEA StatiCa Detalle
3D CSFM define el comportamiento del hormigón basándose en la teoría de plasticidad de Mohr-Coulomb para cargas monótonas.
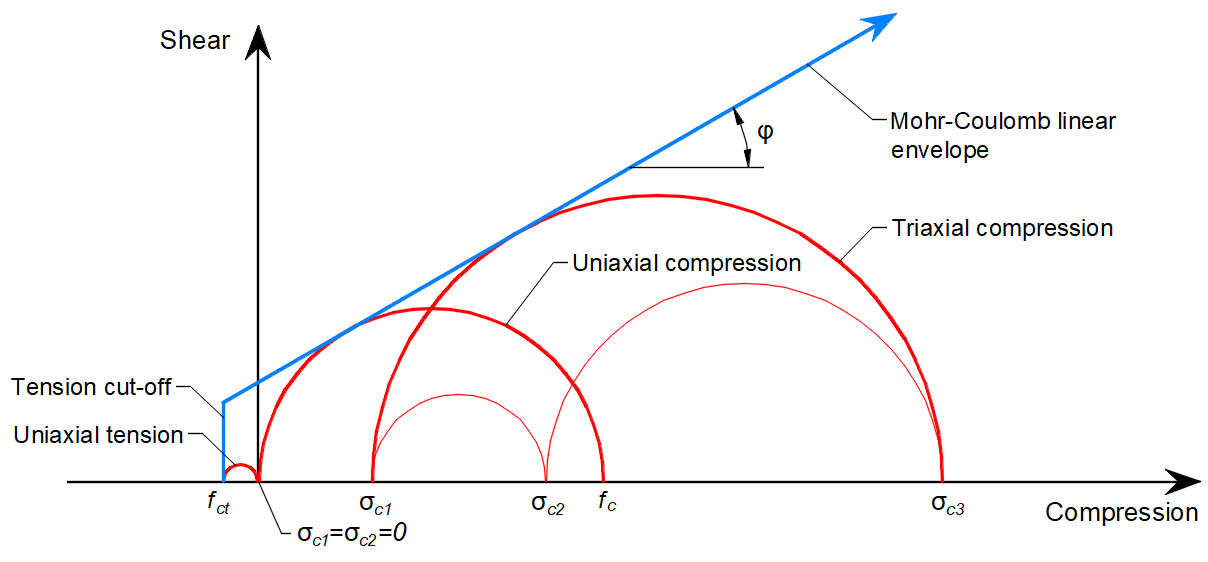
En general, para un ángulo dado de fricción interna del hormigón, que está alrededor de φ = 30°, las resistencias a tracción y compresión de los círculos de Mohr del hormigón pueden construirse como en la Figura 2.
\[ \textsf{\textit{footnotesize{Fig. 2\qquad Círculos de Mohr para hormigón}}]
Donde fc es la resistencia del hormigón en compresión, fct es la resistencia del hormigón en tracción, φ es el ángulo de fricción interna, y σc1, σc3 son las tensiones principales del hormigón bajo compresión triaxial.
Puede observarse que a medida que aumenta la tensión principal σc3, también aumenta la diferencia máxima posible entre los valores de σc3 y σc1, que definimos como σc,eq máxima (véase más adelante).
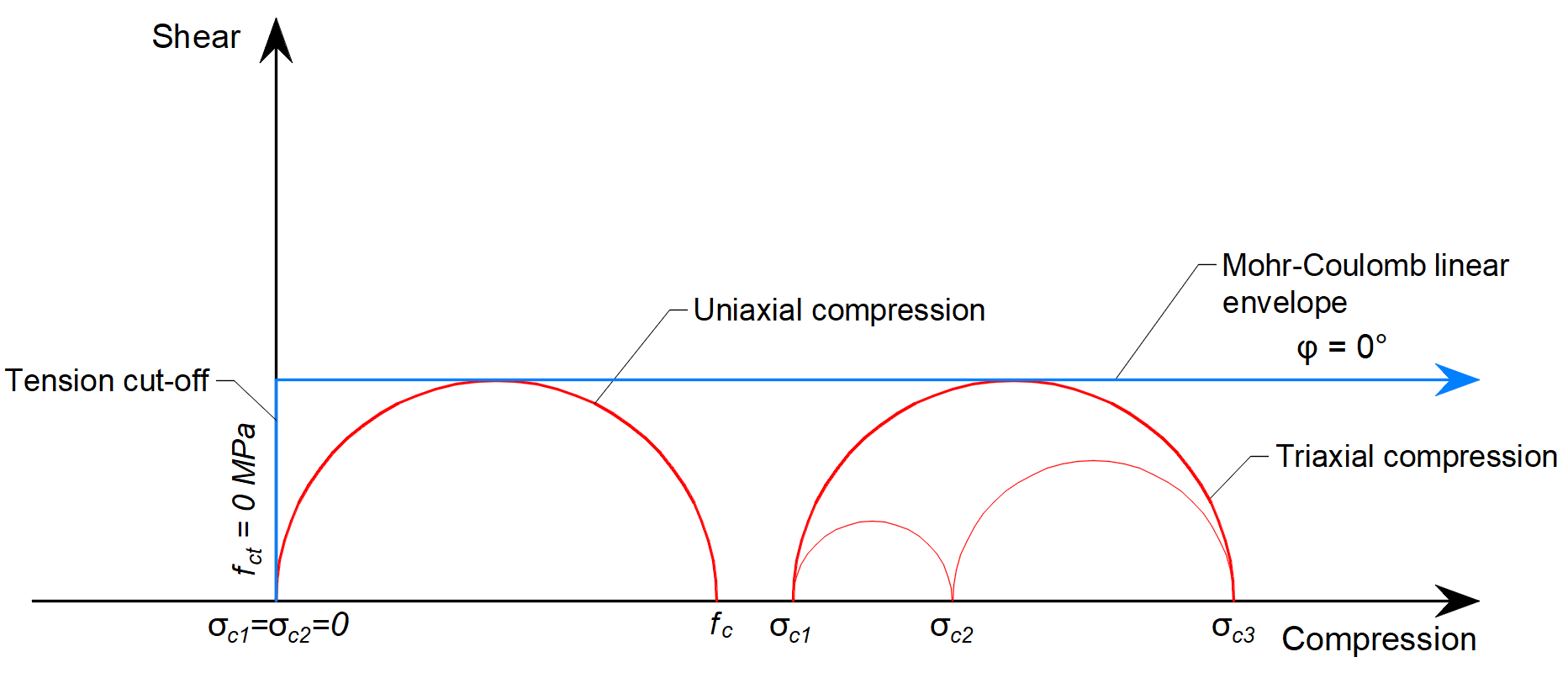
En 3D CSFM como se implementa en IDEA StatiCa Detail, el ángulo de fricción interna se considera como φ = 0°, como se muestra en la Figura 3.
\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Círculos de Mohr para hormigón implementados en IDEA StatiCa Detail}}]
La consecuencia práctica de esta implementación es que la diferencia máxima entre σc3 y σc1 es constante a medida que aumenta σc3.
Tensión principal equivalente expresa la tensión uniaxial "perjudicial" equivalente para un estado de tensión triaxial general.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
El valor σc, eq puede, por tanto, compararse directamente con los límites de resistencia uniaxial según los códigos.
Comparando la Figura 2, en la que se utiliza el ángulo real de rozamiento interno, y la Figura 3, que muestra la aplicación de la teoría de Mohr-Coulomb con un ángulo de rozamiento interno nulo, puede observarse que el enfoque elegido para los cálculos en la aplicación Detalle es muy conservador para la evaluación del estado tensional triaxial. Obsérvese que el modelo con ángulo de rozamiento nulo se asemeja al modelo de Tresca, con corte de tensión.
Leer más en Diseño estructural de discontinuidades 3D de hormigón en IDEA StatiCa Detail
Ensayo triaxial - un ejemplo de confinamiento activo
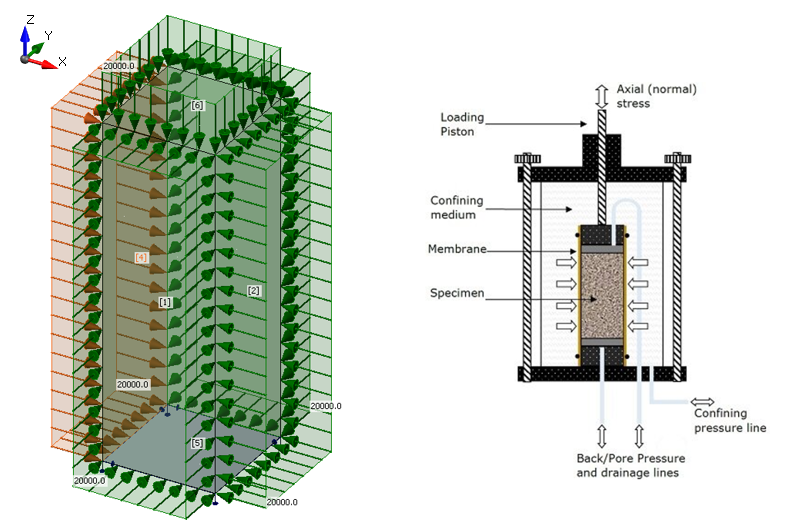
En el ejemplo, simularemos un ensayo triaxial para explicar cómo se implementa el efecto de presión triaxial en 3D CSFM en IDEA StatiCa Detail. Este será, por lo tanto, un ejemplo de confinamiento activo. Todos los cálculos serán en valores característicos.
El modelo es del tipo de bloque sólido con dimensiones en planta de 1.0 x 1.0 m y una altura de 3.0 m hecho de concreto C30/37 soportado por un soporte rígido de superficie en la dirección Z. Sólo en aras de la estabilidad del modelo de análisis, se incluyen también las direcciones X e Y en el apoyo superficial con un valor de rigidez despreciable. La carga se aplica en dos etapas. En el primer paso, se aplica al modelo una presión hidrostática (σc,1 = σc,2 = σc,3) de 20 MPa. Este alto valor, relativo a la resistencia del hormigón, se eligió principalmente para demostrar la estabilidad del modelo computacional.
\[ \textsf{\textit{footnotesize{Fig. 4\qquad Configuración de ensayo triaxial - modelo, carga y condiciones de contorno}}]
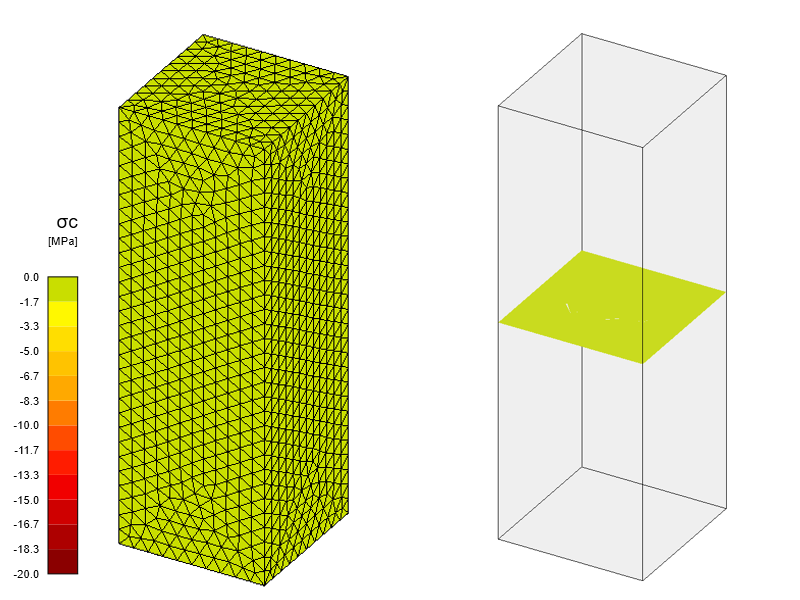
Después de calcular el modelo, obtenemos el valor σc,eq = 0 MPa en todo el modelo. Esto corresponde a la definición anterior de la aplicación de la teoría de la plasticidad de Mohr-Coulomb en Detalle.
\[ \textsf{\textit{footnotesize{Fig. 5\qquad Tensión Principal Equivalente - primer paso de cálculo}}]
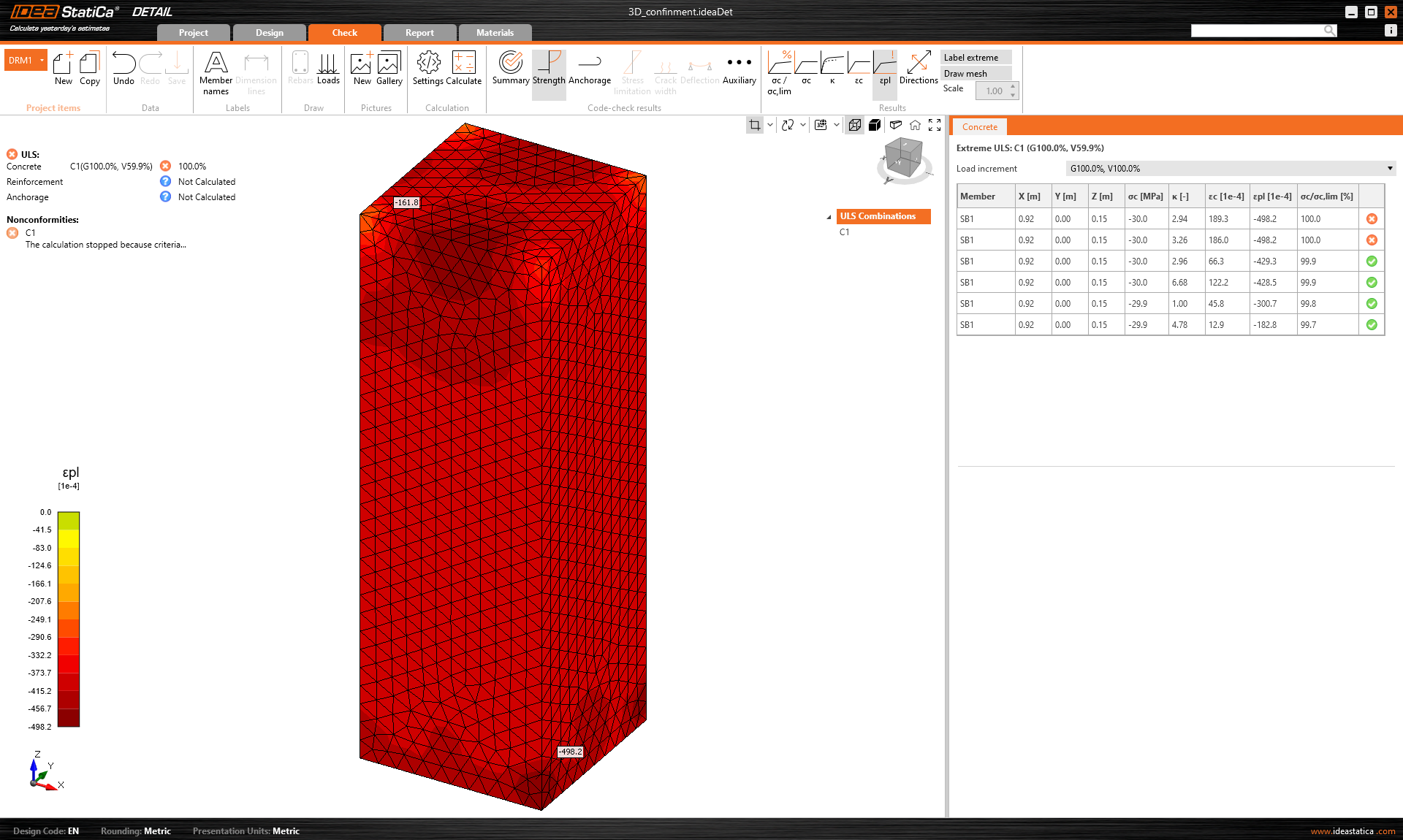
En el segundo paso, se aplica una carga superficial de 50 MPa a la superficie superior del modelo. Obsérvese que esta carga es superior a la resistencia a compresión axial del hormigón considerada de 30 MPa. El objetivo de la prueba es demostrar que en este paso no se aplicará ninguna carga superior a la resistencia a compresión del hormigón. Por lo tanto, el cálculo debe detenerse de modo que la carga aplicada sea igual al valor resultante de σc,eq.
Veamos ahora los resultados. Como era de esperar, el cálculo se detuvo porque se superó el criterio de deformación plástica en el hormigón, que es del 5%.
\[ \textsf{\textit{footnotesize{Fig. 7\qquad Resultado del cálculo tras el segundo paso}}}]
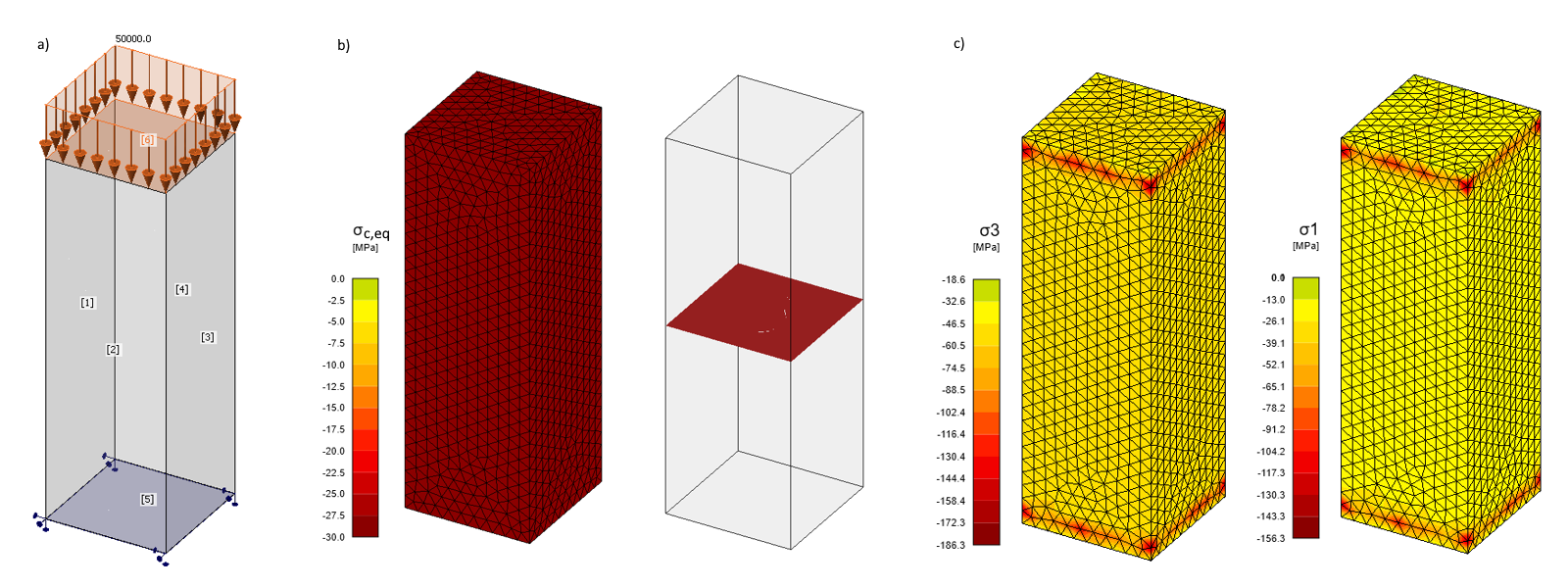
Si repasamos los resultados, comprobamos que coinciden con los supuestos definidos anteriormente. Esto demuestra que el modelo concreto en Detalle funciona correctamente en términos de confinamiento activo.
\[ \textsf{\textit{footnotesize{Fig. 7\qquad a) Carga aplicada en el paso 2; b) Tensión principal equivalente; c) Tensiones principales σc,3 a σc,1}}}]
Los picos de tensión que se observan en las superficies superior e inferior se deben a la forma de aplicar la carga superficial y el apoyo superficial en los bordes de la malla a partir de elementos tetraédricos con rotaciones nodales. Y también al hecho de que los valores nodales máximos de los elementos finitos adyacentes se muestran siempre en la aplicación Detalle. Sin embargo, el tema de este artículo no es la especificación de este método, por lo que no profundizaremos en él.
Verificación ABAQUS
En el siguiente paso, veremos una comparación con modelos creados en ABAQUS, donde también se utiliza la teoría de plasticidad de Mohr-Coulomb para definir el hormigón. Compararemos los resultados de Detail con un modelo de hormigón real con un ángulo de rozamiento interno de 30°. De este modo, demostramos la conservabilidad del enfoque en 3D CSFM.
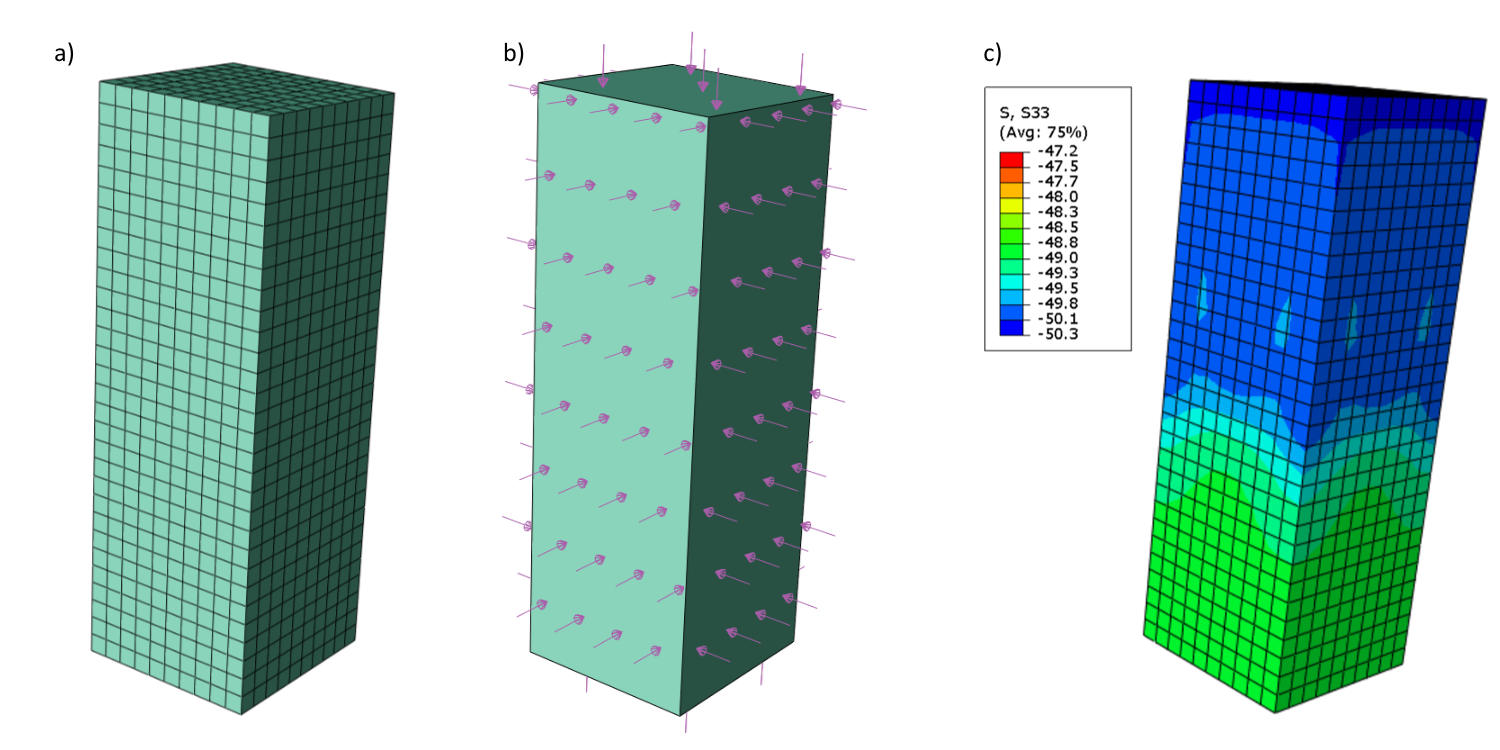
\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Modelo ABAQUS: a) Malla de hormigón 2; b) Definición de cargas; c) Tensiones principales σc,3}}]
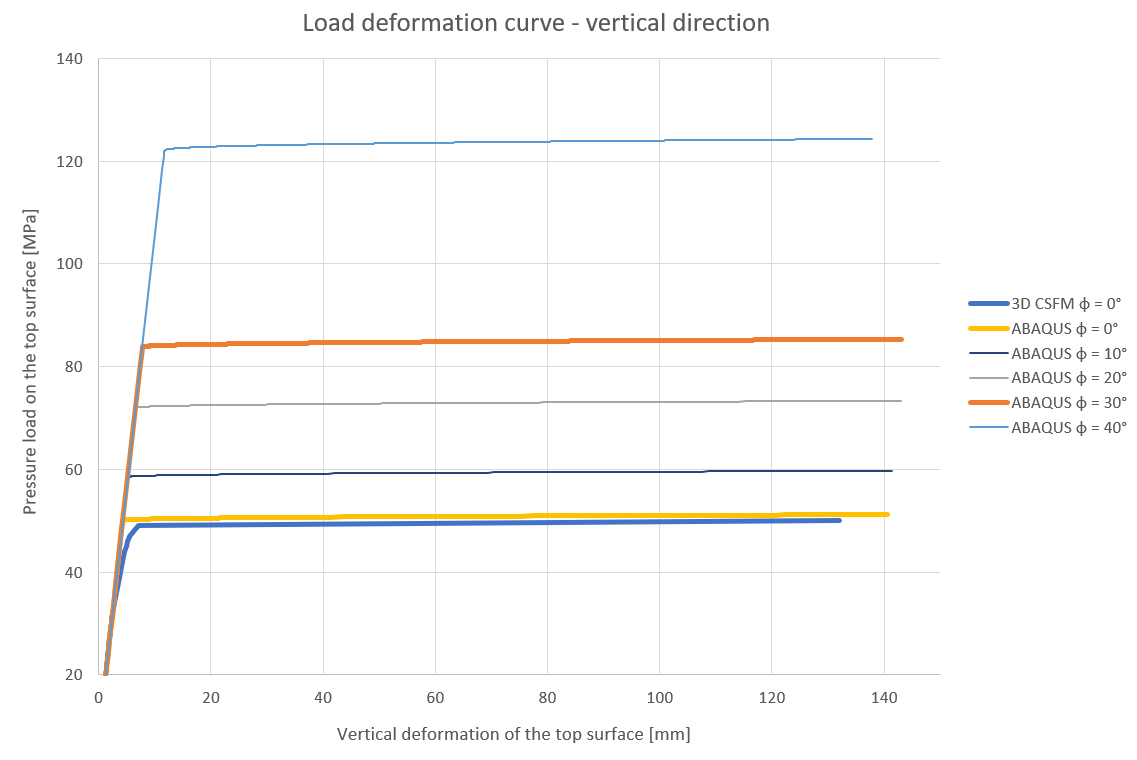
En ABAQUS, creamos un modelo similar al modelo en Detalle. Las definiciones de material, condiciones de contorno y cargas son idénticas. Por otra parte, la malla de hormigón se ha simplificado. Los resultados de dos cálculos, uno utilizando φ = 0°; c = 15 MPa y el segundo φ = 30°; c = 8,65 MPa, se muestran en el gráfico siguiente, así como la comparación con otros ángulos de rozamiento interno φ = 10°, 20°, 40°.
\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Comparación de 3D CSFM, un modelo ABAQUS con varios ángulos de fricción interna }}}]
El gráfico muestra la coincidencia entre los modelos 3D CSFM y ABAQUS para φ = 0°. También se ilustra claramente que las simplificaciones en la definición del material de hormigón en 3D CSFM (la rama plástica horizontal del diagrama tensión-deformación y la envolvente lineal horizontal de Mohr-Coulomb), que conducen a una mayor claridad y, lo que es más importante, a un cálculo más rápido, también conducen, al menos en términos de tensión triaxial, a resultados conservadores.
Como último punto, cabe mencionar que si consideramos una tensión hidrostática superior a 20 MPa, la diferencia entre los modelos φ = 0° y otros ángulos sería aún mayor.
Conclusión
Se demostró y explicó que el cálculo en 3D CSFM es consistente con los supuestos reportados en los Antecedentes Teóricos. Esto se verificó mediante la comparación con los modelos ABAQUS y se demostró el conservadurismo del enfoque 3D CSFM para el fenómeno de la tensión triaxial.