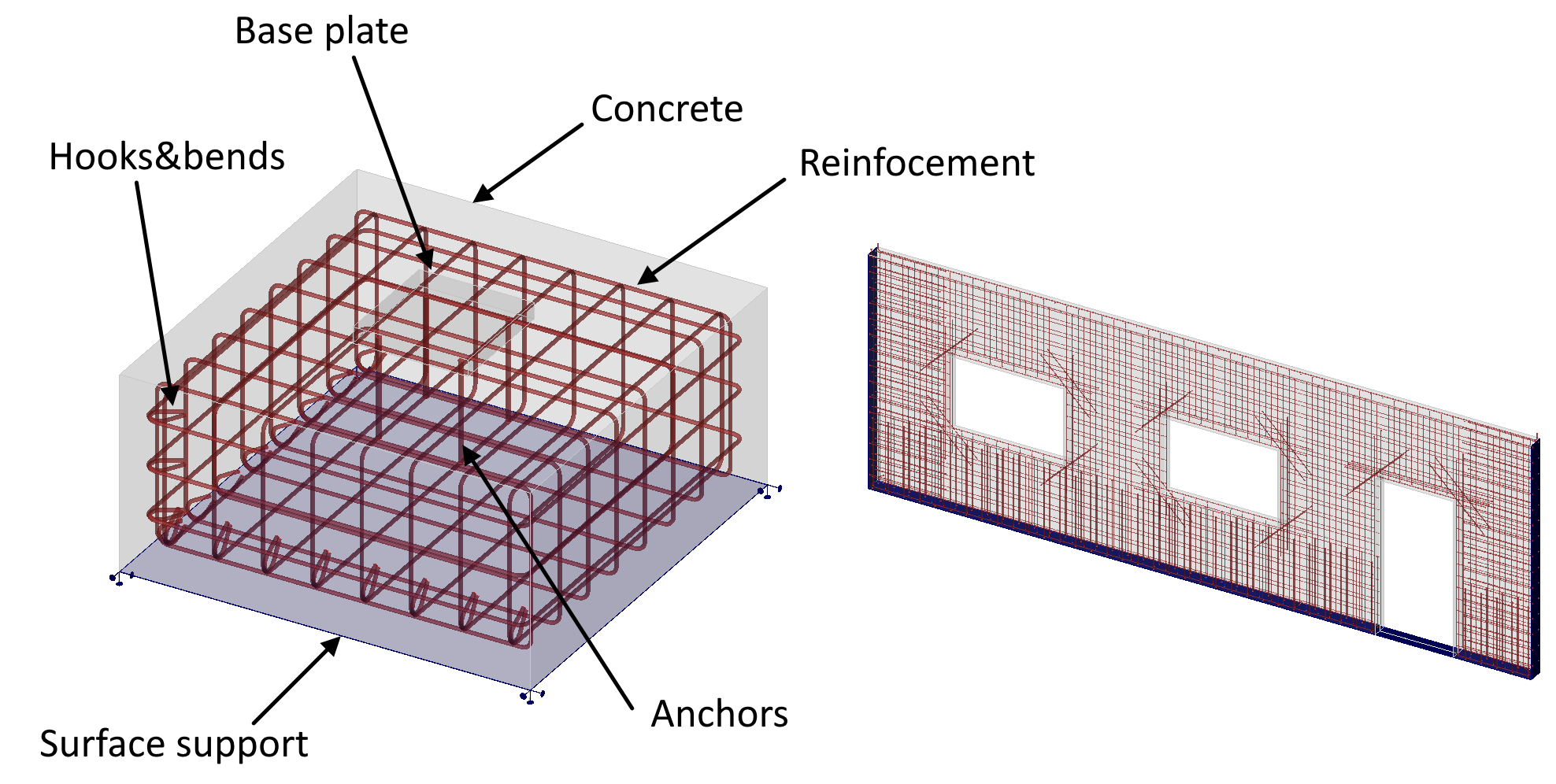
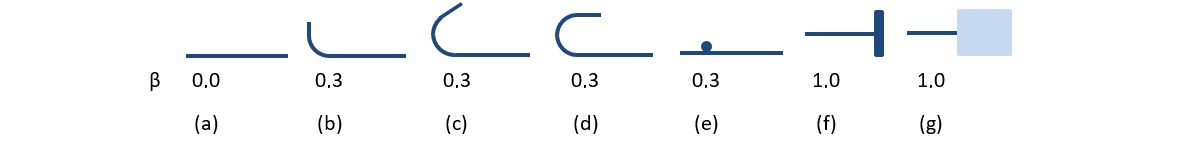IDEA StatiCa Detail - Dimensionamento estrutural de descontinuidades 3D em betão
Dimensionamento estrutural de descontinuidades 3D de betão no IDEA StatiCa Detail
Introdução ao método 3D CSFM
Introdução geral para o dimensionamento estrutural de detalhes 3D de betão
Principais hipóteses e limitações
Implementação da teoria da plasticidade de Mohr-Coulomb no CSFM3D
Hipóteses de mecânica geral para o CSFM 3D
Modelo de análise do IDEA StatiCa 3D Detail
Introdução à implementação de elementos finitos
Tipos de elementos finitos
Dispositivos de transferência de carga
Malha em 3D CSFM
Método de solução e algoritmo de controlo de carga para 3D CSFM
Apresentação de resultados 3D
Modelo importado de IDEA StatiCa Connection
Verificação do modelo
Verificações estruturais de acordo com o EUROCODE
- Modelos de materiais em 3D CSFM (EN)
- Factores de segurança parciais
- Verificações do estado limite último
Verificações estruturais de acordo com o ACI 318-19
- Modelos de materiais em 3D CSFM (ACI)
- Redução da resistência e factores de carga
- Verificações de resistência
Introdução ao método CSFM 3D
Uma introdução geral à conceção estrutural de pormenores 3D em betão
Na prática, os engenheiros podem encontrar diferentes tipos de elementos finitos (desde simples elementos de barra 1D até elementos de tijolo 3D mais complicados) que são utilizados numa variedade de aplicações para a análise e projeto de elementos estruturais. Uma caraterística comum da maioria dos cálculos na prática tende a ser o comportamento linear dos modelos, cujas vantagens são, sem dúvida, a rapidez, a clareza e simplesmente o facto de, para uma grande variedade de problemas, esta solução ser suficiente.
Especialmente no mundo das estruturas de betão, acontece frequentemente que a abordagem linear não é suficiente, simplesmente porque após o aparecimento das primeiras fissuras no elemento carregado, as tensões são redistribuídas e o problema torna-se significativamente não linear.
Para estes casos, é necessário escolher uma das abordagens mais sofisticadas. Para casos 1D, é frequente encontrar métodos analíticos definidos diretamente nos códigos. Por exemplo, os populares modelos Strut e Tie podem ser construídos para elementos planos 2D e regiões de descontinuidade (regiões D), ou o método de campo de tensão mais sofisticado implementado no IDEA StatiCa Detail, CSFM, pode ser utilizado.
No entanto, se o engenheiro se deparar com um problema que não pode ser simplificado para o comportamento planar, as opções são muito limitadas. Naturalmente, um modelo 3D de escora e tirante pode ser construído ou um software semi-científico pode ser utilizado para uma análise precisa. Esses procedimentos geralmente são demorados, não estão em conformidade com o código e exigem um engenheiro com conhecimento em métodos de modelagem avançados.
Por este motivo, a IDEA StatiCa desenvolveu e implementou o 3D CSFM (Compatible Stress Field Method) na aplicação Detail. O 3D CSFM estende o CSFM estabelecido para uma terceira dimensão, oferecendo uma solução rápida e em conformidade com o código que é principalmente aplicável ao engenheiro do dia a dia, dando-lhe uma nova capacidade única para abordar com segurança os detalhes complexos das estruturas de betão.
Principais pressupostos e limitações
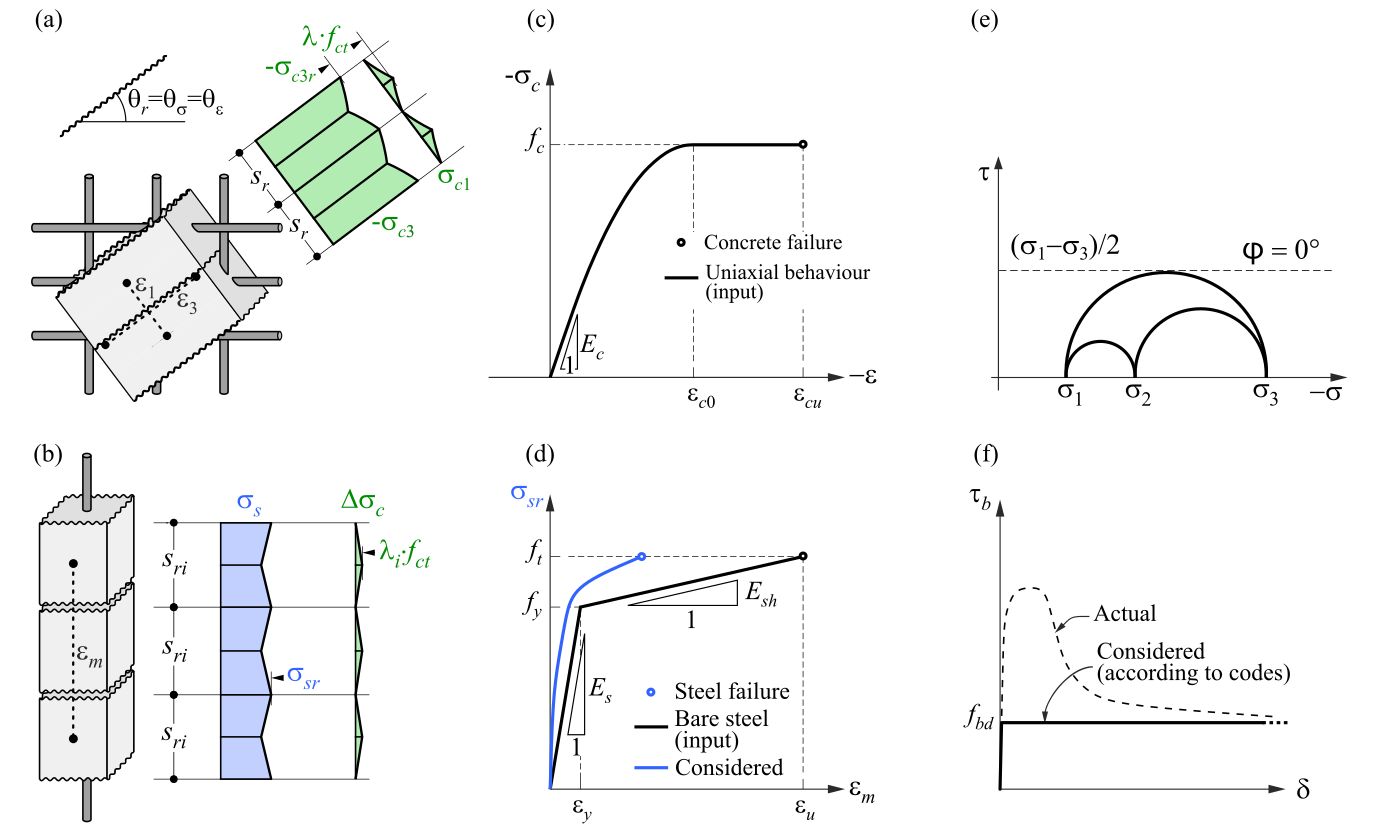
O CSFM 3D define o comportamento do betão com base na teoria da plasticidade de Mohr-Coulomb modificada para cargas monotónicas. O método considera as tensões principais do betão na compressão e as tensões da armadura (σsr) nas fissuras, negligenciando a resistência à tração do betão (corte de tensão), exceto o seu efeito de reforço na armadura (reforço de tensão).
σc1r, σc2r, σc3r ≤ 0 MPa
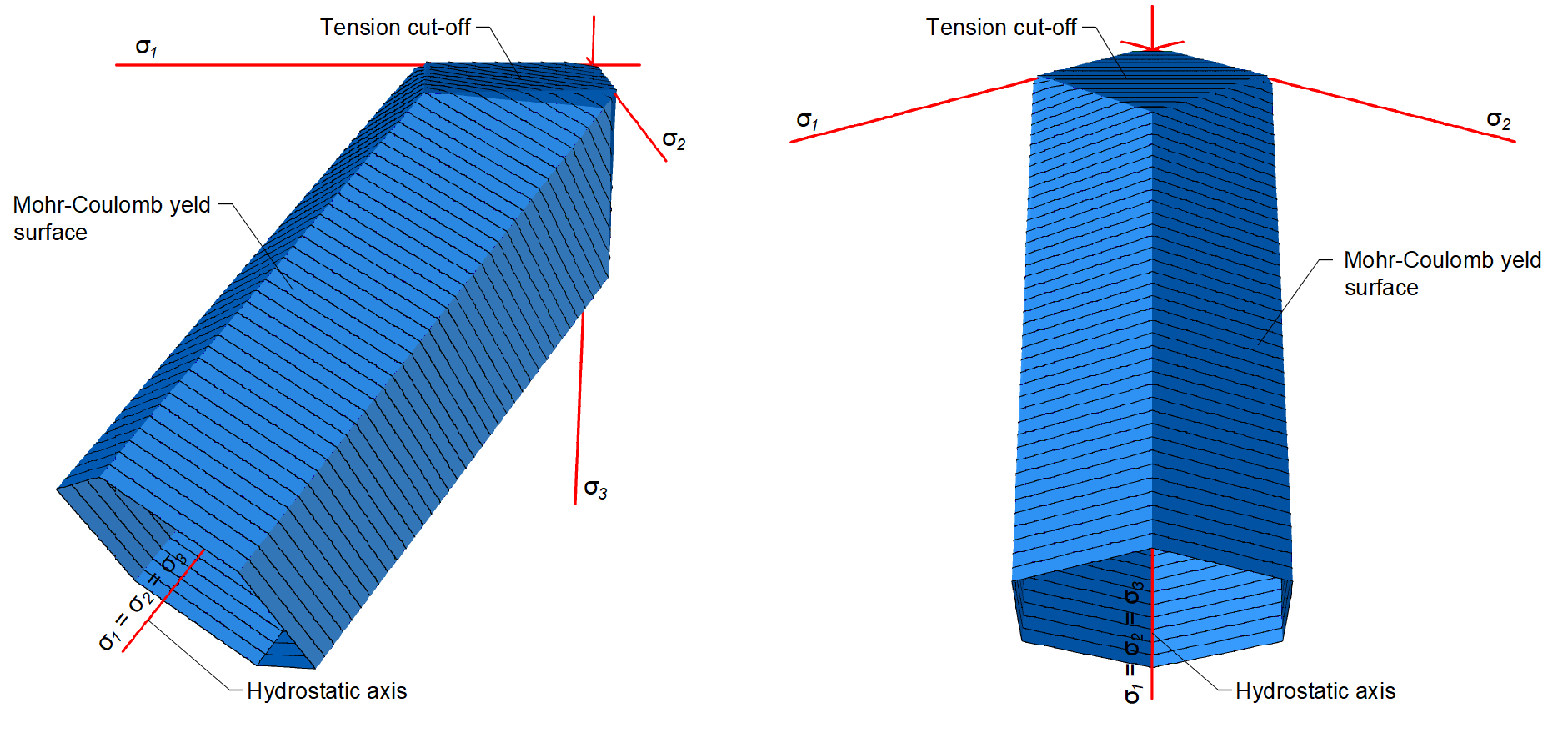
Os varões de reforço estão ligados aos elementos finitos do volume de betão através de elementos de ligação, permitindo o deslizamento entre o betão e o reforço. É de notar que o CSFM 3D não é adequado para simular betão simples devido à ausência de tensão, o que pode resultar em deformações enganadoras e divergência de modelos. De um modo geral, a teoria de Mohr-Coulomb inclui duas propriedades fundamentais que regem a evolução da superfície de plasticidade em compressão e parcialmente em tração: o ângulo de atrito interno φ e o parâmetro de coesão c. O CSFM 3D assume um ângulo de atrito interno nulo (Fig. 1e), conduzindo a um dimensionamento conservador devido à semelhança da superfície de plasticidade com o modelo de Tresca, que é independente do primeiro invariante de tensão.
\( \textsf{\textit{\footnotesize{Fig. 1\qquad Pressupostos básicos do CSFM 3D: (a) tensões principais no betão; (b) tensões na direção da armadura;}}}\) \( \textsf{\textit{\footnotesize{(c) diagrama tensão-deformação do betão em termos de tensões máximas; (d) diagrama tensão-deformação da armadura}}\) \( \textsf{\textit{\footnotesize{em termos de tensões nas fissuras e deformações médias; (e) círculos de Mohr para o modelo de betão em CSFM 3D; (f) tensão de corte da ligação - deslizamento}}\) \( \textsf{\textit{\footnotesize{relação para verificações do comprimento de ancoragem.}}}\)
Betão
O modelo de material apresentado é um modelo de plasticidade multi-superfície dado pela combinação dos modelos de Mohr-Coloumb e Rankine para carregamento monotónico. É importante notar que este modelo não aborda a descarga, pelo que as variáveis de estado não são armazenadas, como seria o caso nos modelos clássicos de plasticidade utilizados para cargas cíclicas.
\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Mohr-Coulomb multi-surface plasticity model for friction angle 0 degree}}}\]
Como já foi referido, o modelo de material destina-se a ser utilizado em aplicações que calculam a resposta do betão armado (não é adequado para betão simples). Isto deve-se à exclusão do betão em tração. Por conseguinte, o modelo nem sequer é adequado para elementos estruturais em que as regras de dimensionamento do betão armado, tais como a taxa de armadura mínima, o espaçamento máximo entre barras, etc., não são cumpridas. Deve também ser acrescentado que, por razões de estabilidade numérica, é definida uma capacidade de tração muito pequena no modelo. A parte de tração é limitada por planos correspondentes ao modelo de Rankine.
O modelo CSFM 3D no IDEA StatiCa Detail não considera um critério de rotura explícito em termos de deformações para o betão em compressão (ou seja, considera um ramo infinitamente plástico após a tensão de pico ser atingida). Esta simplificação não permite a verificação da capacidade de deformação das estruturas que roem à compressão. No entanto, a sua capacidade última é corretamente prevista quando o aumento da fragilidade do betão à medida que a sua resistência aumenta é considerado através do fator de redução𝜂𝑓𝑐 definido no fib Model Code 2010 da seguinte forma:
\[f_{c,red} = \eta _{fc} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{{30}}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
onde:
fc é a resistência caraterística do cilindro de betão (em MPa para a definição de \ ( \eta_{fc} \)).
A fc,red é então comparada com a Tensão Principal Equivalente σc,eq no betão, que será definida mais tarde, naturalmente, com a consideração de todos os factores de segurança prescritos pelo código.
Uma descrição detalhada do modelo de betão pode ser encontrada na seguinte ligação:
Reforço
O diagrama bilinear tensão-deformação para varões de armadura, tal como definido pelos códigos de projeto (Fig. 1d), representa um modelo idealizado. Este modelo requer o conhecimento das propriedades básicas da armadura durante a fase de projeto, especificamente a classe de resistência e ductilidade. Em alternativa, os utilizadores têm a opção de definir uma relação tensão-deformação personalizada.
A rigidez à tração é considerada através da modificação da relação tensão-deformação do varão de reforço nu para captar a rigidez média dos varões embebidos no betão (εm) (Fig. 1b).
Ancoragem
O deslizamento da ligação entre a armadura e o betão é introduzido no modelo de elementos finitos considerando a relação constitutiva simplificada rígida-perfeitamente plástica apresentada na (Fig. 1f), sendo fbd o valor de projeto (valor facturado) da tensão última da ligação especificada pelo código de projeto para as condições específicas da ligação.
Este é um modelo simplificado com o único objetivo de verificar as prescrições de ligação de acordo com os códigos de projeto (i.e., ancoragem do reforço). A redução do comprimento de ancoragem quando se utilizam ganchos, laços e formas de barra semelhantes pode ser considerada através da definição de uma determinada capacidade na extremidade da armadura, como será descrito mais adiante.
Ancoragens
O elemento da ancoragem é definido como sendo capaz de transferir forças normais de tração ou compressão, bem como forças de corte, considerando também a rigidez à flexão. No entanto, apenas é avaliada a tensão normal nas ancoragens.
Estão disponíveis dois tipos de ancoragens:
- Ancoragem adesiva
- Reforço no local
O comportamento da armadura de betão armado é o mesmo que o da armadura clássica (tipo de ancoragem, ligação, etc.) . Para as ancoragens adesivas, é possível definir diretamente o valor de projeto da resistência da ligação. Este valor deve ser lido na ficha técnica do fabricante.
Mohr-Coulomb plasticity theory implementation in 3D CSFM
In the following chapter, we will take a look at how the Mohr-Coulomb theory is implemented in 3D CSFM. We will explain how the confinement effect (triaxial stress) is considered and how the Equivalent Principal Stress σc,eq is calculated, which is used to determine the load-bearing capacity from the point of view of concrete.
Introduction to the theory
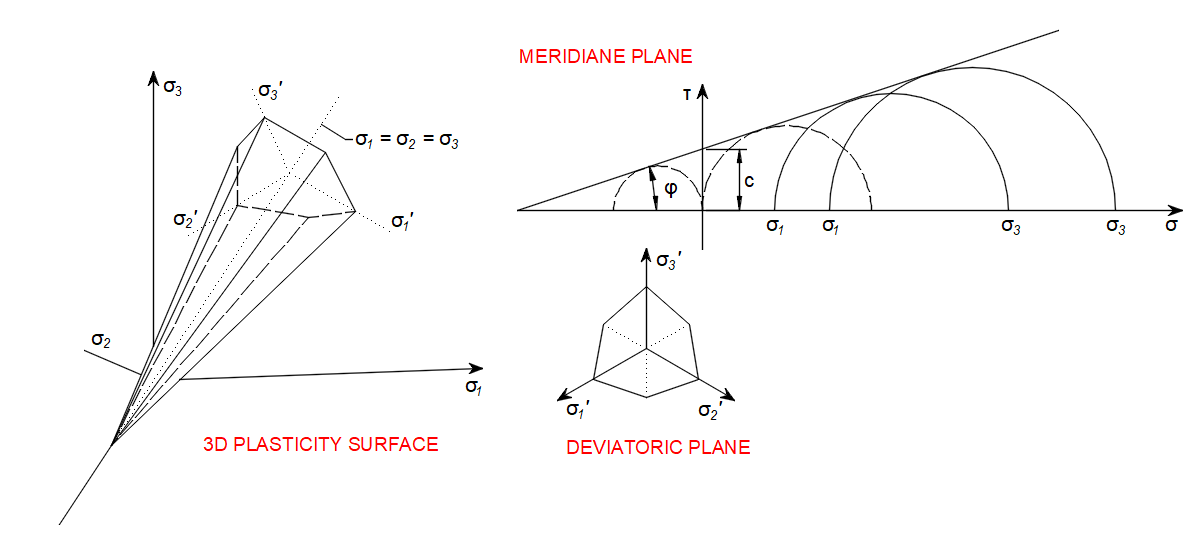
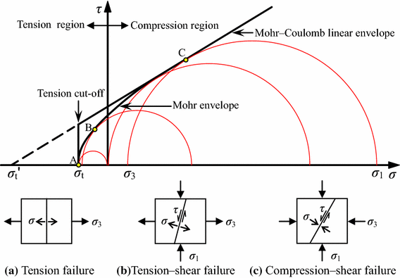
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials, to shear and normal stress. Most of the classical engineering materials follow this rule in at least a part of their shear failure envelope. Generally, the theory applies to materials for which the compressive strength far exceeds the tensile strength.
\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Mohr-Coulomb Plasticity Model }}}\]
In structural engineering, it is used to determine failure load as well as the angle of fracture for displacement of fracture surface in concrete and similar materials. Coulomb's friction hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. Mohr's circle is used to determine which principal stresses will produce this combination of shear and normal stress and the angle of the plane in which this will occur. According to the principle of normality, the stress introduced at failure will be perpendicular to the line describing the fracture condition.
\[ \textsf{\textit{\footnotesize{Fig. 4\qquad Meridian plane and tension cut-off}}}\]
It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the angle of friction. This makes the strength of the material determinable by comparing the external mechanical work introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By conservation of energy, the sum of these must be zero and this will make it possible to calculate the failure load of the construction.
Implementation in 3D CSFM
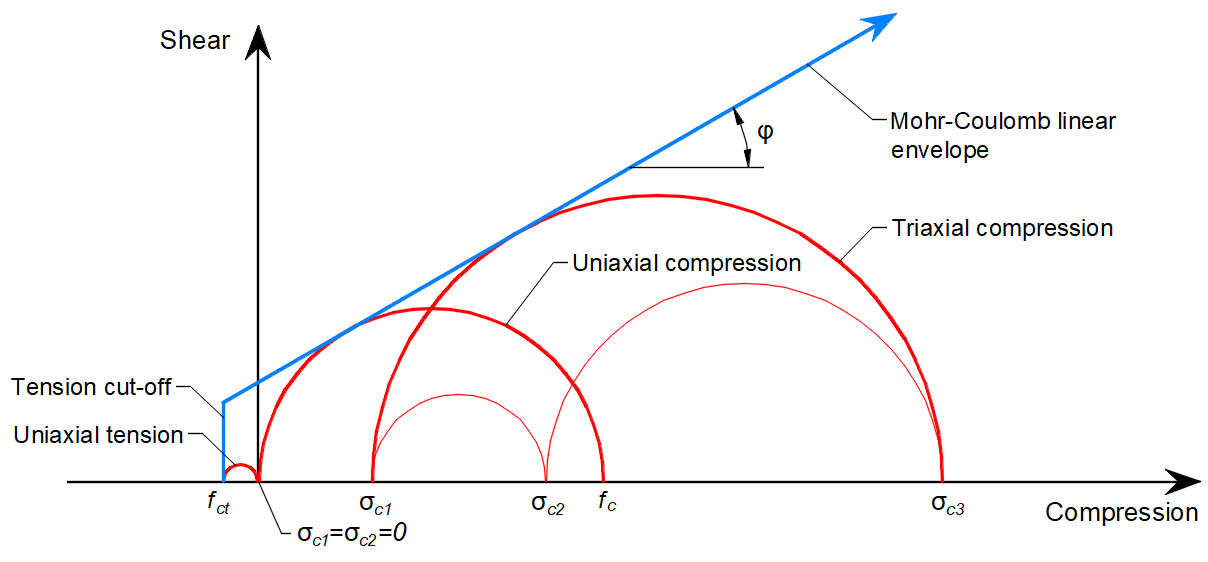
In general, for a given angle of internal friction of the concrete, which is around φ = 30-40° in Reference [1], [2], [3], [4], the tensile and compressive strengths of the concrete Mohr's circles can be constructed as in Figure 5.
\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Mohr's circles for concrete}}}\]
Where fc is concrete strength in compression, fct is concrete strength in tension, φ is the angle of internal friction, and σc1, σc3 are the principal stresses of concrete under triaxial compression.
It can be noticed that as the principal stress σc3 increases, the maximal possible difference between the values of σc3 and σc1, which we define as maximal σc,eq (see below), also increases. This difference corresponds to twice the deviatoric stress defined in the literature as a radius of the mohr circles.
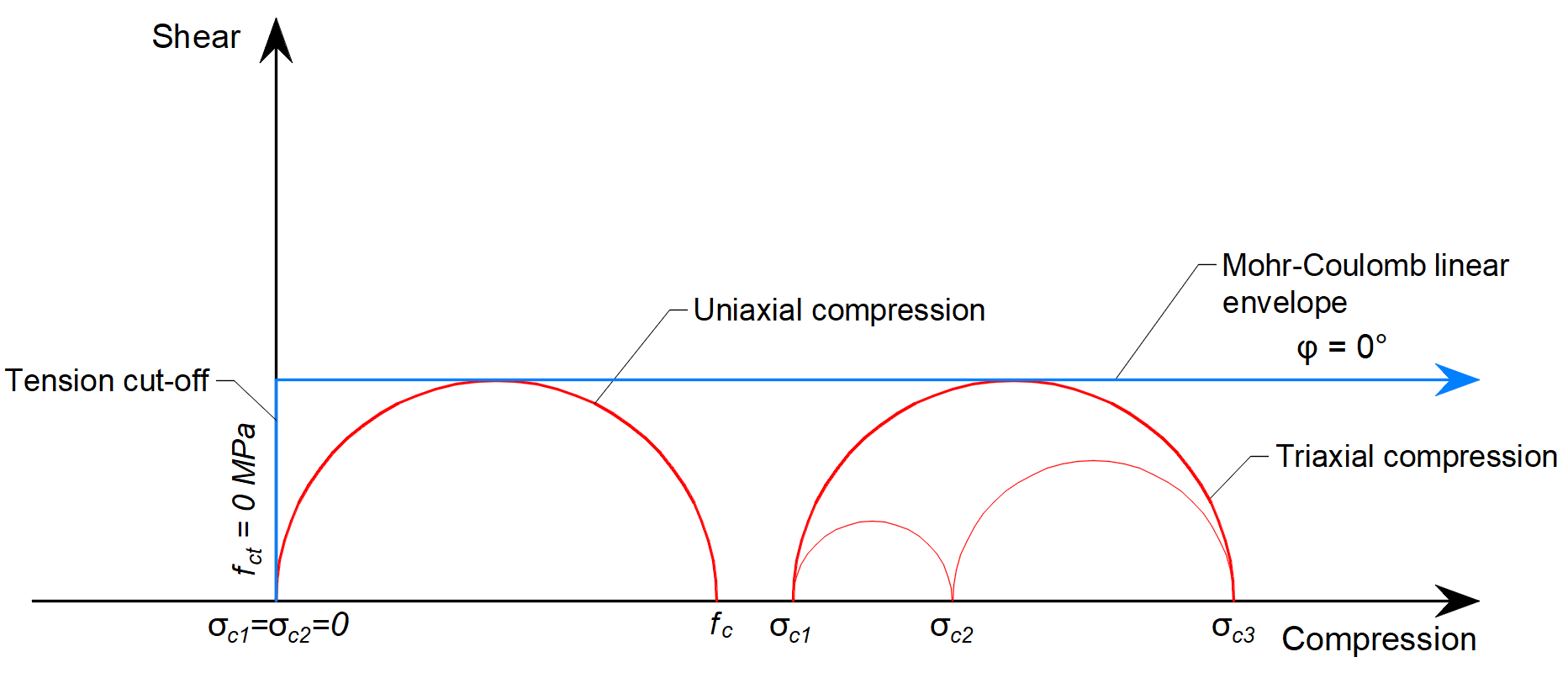
In 3D CSFM implemented in IDEA StatiCa Detail, the angle of internal friction is considered as φ = 0°, as shown in Figure 6.
\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Mohr's circles for concrete implemented in IDEA StatiCa Detail}}}\]
The practical consequence of this implementation is that the maximum difference between σc3 and σc1 is constant as σc3 increases.
Equivalent Principal Stress expresses the equivalent uni-axial stress for a general tri-axial stress state.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
The σc,eq value can, therefore, be directly compared with uniaxial strength limits according to codes.
\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} \le 1\]
Where σc,lim is the design (factored) uniaxial strength of concrete fc.
Comparing Figure 5, where the real angle of internal friction is used, and Figure 6, which shows the Mohr-Coulomb theory implementation with zero angle of internal friction, it can be seen that the approach chosen for the calculations in Detail is very conservative for the assessment of triaxial stress state.
For a better understanding of the areas affected by tri-axial compression stress, the expression of the increase of the effective material strength due to tri-axial compression has been added to the IDEA StatiCa Detail application as a ratio σc3/σc,lim. You can find this ratio in the Strength code check.
In the Auxiliary results, the user can also find the κ factor, which explains the tri-axiality in a different way.
\[\kappa = \frac{ \sigma_{c3}}{ \sigma_{c,eq}}\]
The concrete strength check can be then rewritten as:
\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} = \frac{\sigma_{c,3} }{ \kappa \cdot \sigma_{c,lim}} \le 1\]
It follows from the previous that if the element is under hydrostatic stress - σc3=σc2=σc1, the Equivalent Principal Stress σc,eq will have the zero value, and the kappa factor will reach infinity.
More can be found here: Tri-axial stress – the active confinement effect
Pressupostos da mecânica geral para a CSFM 3D
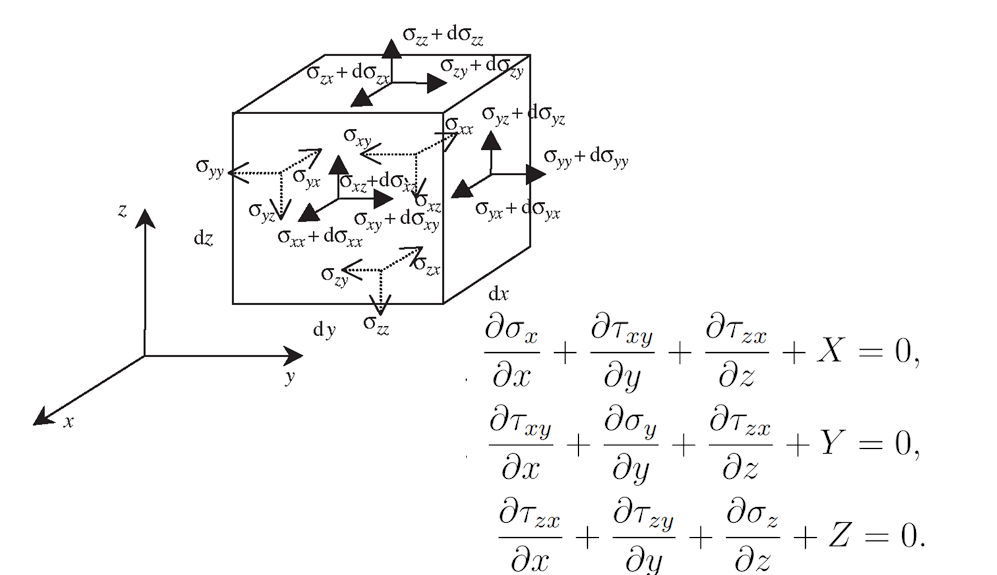
Equações de equilíbrio
A teoria das pequenas deformações permite a montagem da equação de equilíbrio com base no volume não deformado, utilizando uma abordagem de primeira ordem.
\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Equações de equilíbrio e representação gráfica em elemento infinitesimal}}}\]
Equações de compatibilidade
Um corpo sólido é constituído por volumes infinitesimais ou pontos materiais, cada um dos quais está interligado sem intervalos ou sobreposições. As condições matemáticas devem ser respeitadas para evitar a ocorrência de lacunas ou sobreposições quando um corpo contínuo sofre deformação.
Equações constitutivas
As equações constitutivas que regem o comportamento dos elementos 3D desempenham um papel fundamental na análise do comportamento dos materiais em mecânica estrutural. Estas equações são formuladas para acomodar o comportamento isotrópico não linear, que é válido para barras de blocos sólidos no IDEA StatiCa Detail.
Quando se trata de uma parede 3D, é essencial ter em conta o comportamento ortotrópico ao longo da sua espessura, prestando especial atenção à tensão no betão devido à ausência de armadura transversal. A ortotropia é causada pela permissão da tensão no betão numa direção fora do plano. As propriedades do material, como o módulo de elasticidade e o coeficiente de Poisson, permanecem as mesmas.
\[ \textsf{\textit{\footnotesize{Fig. 8\qquad Matriz de conformidade isotrópica linearmente elástica}}}\]
Modelo de análise do IDEA StatiCa 3D Detail
Uma introdução à implementação de elementos finitos
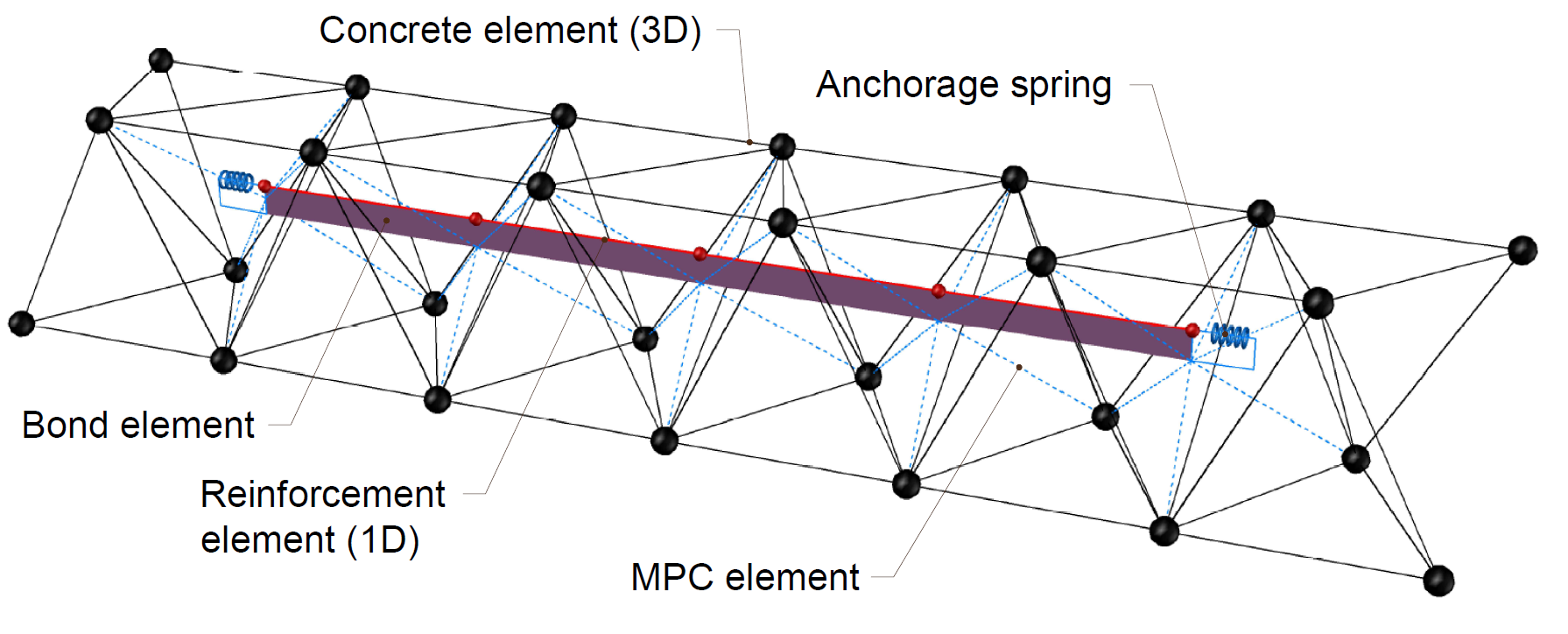
O CSFM 3D considera campos de tensão contínuos no betão (elementos finitos 3D), complementados por elementos de "barra" discretos que representam a armadura (elementos finitos 1D). Assim, a armadura não é difusamente incorporada nos elementos finitos 3D do betão, mas explicitamente modelada e ligada a eles.
\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Renderização do modelo de cálculo para bloco de betão e parede fora do plano}}}\]
Tipos de elementos finitos
O modelo de análise de elementos finitos não linear (inelástico) é criado por vários tipos de elementos finitos utilizados para modelar o betão, a armadura e a ligação entre eles. Os elementos de betão e de armadura são inicialmente malhados de forma independente e depois interligados através de restrições multiponto (elementos MPC). Isto permite que o reforço ocupe qualquer posição não limitada aos nós da malha tetraédrica. Para verificar o comprimento da ancoragem, a ligação e a extremidade da ancoragem, são inseridos elementos de mola entre a armadura e os elementos MPC.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Modelo de elementos finitos: elementos de reforço mapeados para a malha de betão utilizando elementos MPC e de ligação}}}\]
Betão
O betão é analisado utilizando elementos tetraédricos mistos com rotações nodais. Os elementos tetraédricos permitem-nos criar malhas em regiões de qualquer topologia, enquanto a formulação implementada garante resultados de deformação precisos (sem tensões de corte espúrias, conhecidas como efeito de bloqueio de corte), mesmo para malhas grosseiras que não seriam adequadas para a formulação de elementos tetraédricos lineares.
É utilizada a integração total. Isto significa que cada elemento está equipado com quatro pontos de integração situados dentro do volume. Esta integração produz um campo preciso de deformação e tensão, permitindo uma avaliação e apresentação suficientes dos resultados em todo o volume. Posteriormente, os critérios de paragem são estabelecidos com base no valor do ponto de integração.
Reforço
As armaduras são modeladas por elementos de "barra" 1D de dois nós (CROD), que apenas têm rigidez axial. Estes elementos são ligados a elementos especiais de "ligação" que foram desenvolvidos para modelar o comportamento de deslizamento entre um varão de reforço e o betão circundante. Estes elementos de ligação são posteriormente ligados por elementos MPC (multi-point constraint) à malha que representa o betão. Esta abordagem permite a criação de malhas independentes para a armadura e para o betão, enquanto a sua interligação é assegurada posteriormente.
Elementos de ligação
O comprimento de ancoragem é verificado através da implementação das tensões de corte de ligação entre os elementos de betão (3D) e os elementos do varão de reforço (1D) no modelo de elementos finitos. Para este efeito, foi desenvolvido o tipo de elemento finito "ligação".
O elemento de ligação é definido como um elemento finito de casca ligado a elementos que representam a armadura pela primeira camada e pela segunda camada à malha de betão através de restrições multiponto (elementos MPC). É de notar que o elemento de ligação é sempre apresentado neste artigo com uma altura diferente de zero, que é, no entanto, definida como infinitesimal no modelo.
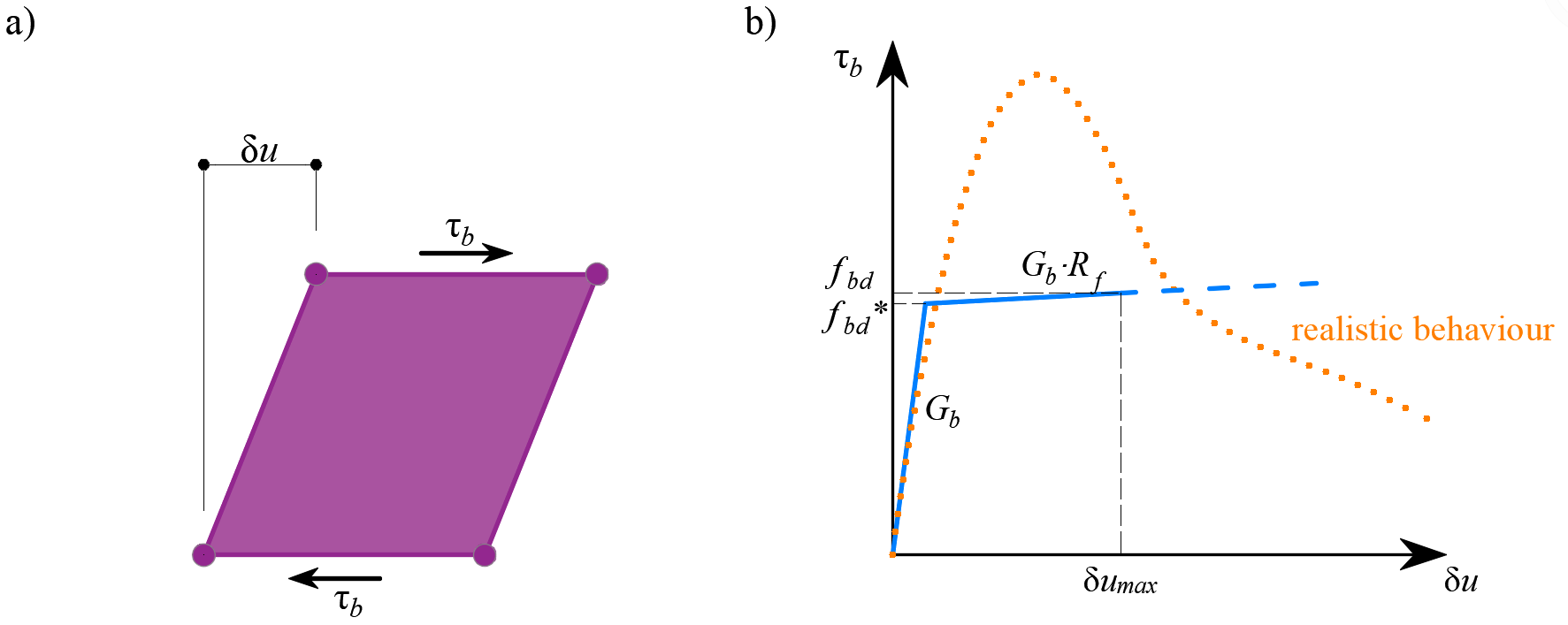
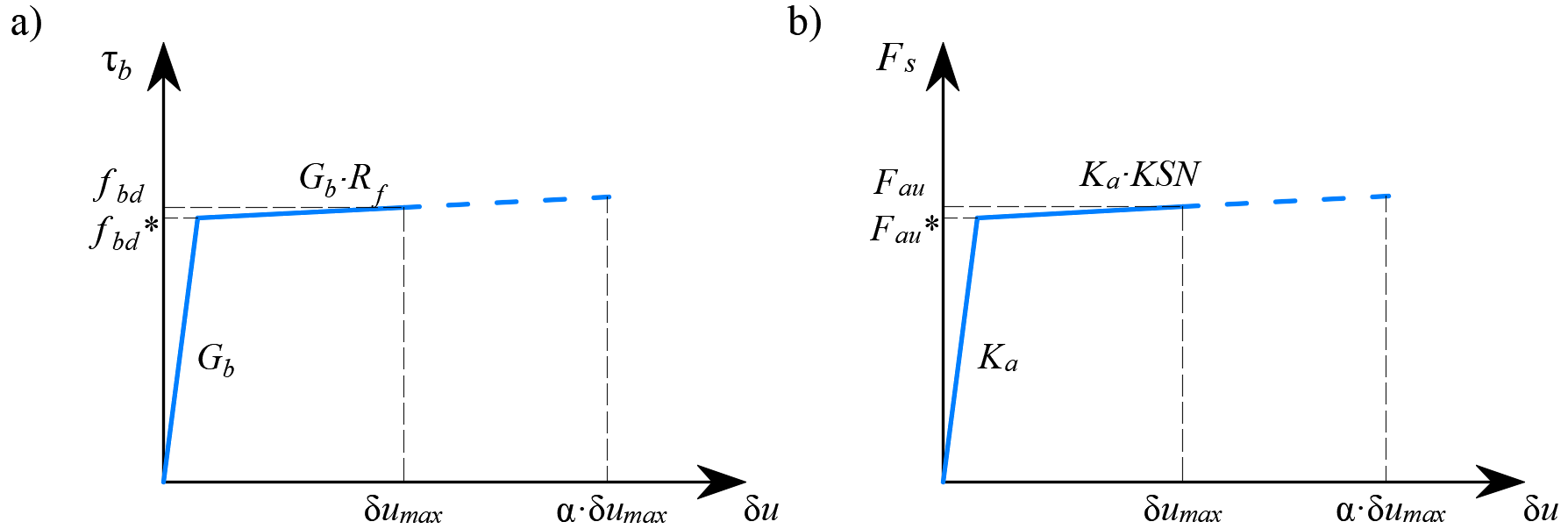
O comportamento deste elemento é descrito pela tensão de ligação, τb, como uma função bilinear do deslizamento entre os nós superior e inferior, δu, ver (Fig. 11).
\[ \textsf{\textit{\footnotesize{Fig. 11\qquad (a) Ilustração concetual da deformação de um elemento de ligação; (b) função de deformação de corte}}}\]
O módulo de rigidez elástica da relação ligação-deslizamento, Gb, é definido da seguinte forma:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
kg coeficiente dependente da superfície do varão de reforço (por defeito, kg = 0,2)
Ec módulo de elasticidade do betão (tomado como Ecm no caso de EN)
Ø o diâmetro do varão de reforço
Os valores de cálculo (valores ponderados) da tensão última de corte da ligação, fbd, fornecidos nos respectivos códigos de cálculo selecionados EN 1992-1-1 ou ACI 318-19 são utilizados para verificar o comprimento da ancoragem. O endurecimento do ramo plástico é calculado por defeito como Gb/105.
Mola de ancoragem
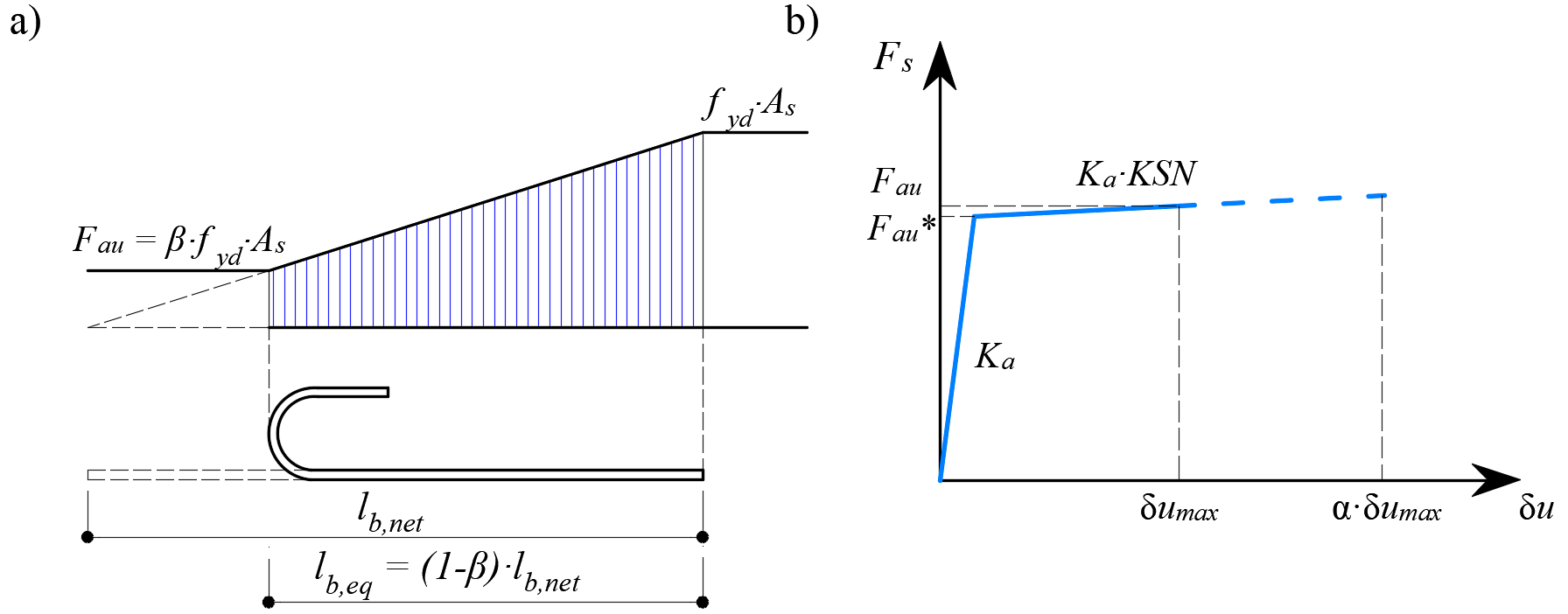
O fornecimento de extremidades de ancoragem aos varões de reforço (i.e., curvas, ganchos, laços...), que cumprem as prescrições dos códigos de dimensionamento, permite a redução do comprimento de ancoragem básico dos varões(lb,net) por um determinado fator β (referido como o "coeficiente de ancoragem" abaixo). O valor de projeto do comprimento de ancoragem(lb) é então calculado da seguinte forma:
\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Modelo para a redução do comprimento de ancoragem: a) Força de ancoragem ao longo do comprimento de ancoragem de }}}\] \[ \textsf{\textit{\footnotesize{a barra de reforço, b) lei constitutiva da força de ancoragem por deslizamento}}\]
A redução do comprimento de ancoragem é incluída no modelo de elementos finitos através de um elemento de mola na extremidade da barra (Fig. 12a), que é definido pelo modelo constitutivo apresentado na (Fig. 12b). A força máxima transmitida por esta mola(Fau) é:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
onde :
β o coeficiente de ancoragem baseado no tipo de ancoragem
Como a secção transversal do varão de reforço
fyd o valor de projeto (valor calculado) da tensão de cedência da armadura
Dispositivos de transferência de carga
Placa de base
A placa de base é modelada como um elemento de casca linear. O material de aço utilizado para as placas de base é definido no separador Materiais. A única propriedade física é o módulo de elasticidade E.
\[ \textsf{\textit{\footnotesize{Fig. 13\qquad A definição do material da placa de base}}}\]
A placa de base pode ser carregada por uma carga pontual (Fx, Fy, Fz, Mx, My, Mz) e por um grupo de forças (Fx, Fy, Fz), utilizado principalmente para carregar modelos exportados do IDEA StatiCa Connection. Note que as cargas pontuais e os momentos pontuais carregam diretamente o nó correspondente da placa de base. Isto significa que não há redistribuição, apenas pela rigidez da placa de base.
Esta implementação permite importar efeitos de carga da Ligação IDEA StatiCa que são aplicados à placa de base na localização dos elementos finitos de soldadura individuais com o valor e a direção determinados a partir da tensão geral desse elemento finito de soldadura. Para mais informações, consulte o capítulo correspondente deste documento.
O contacto apenas por compressão friccional é definido entre a placa de base e o betão. Para a transferência de cisalhamento, o utilizador pode escolher entre três opções:
- Por ancoragens
- Por fricção
- Por olhal de cisalhamento
O software não permite a combinação destes mecanismos de transferência de cisalhamento.
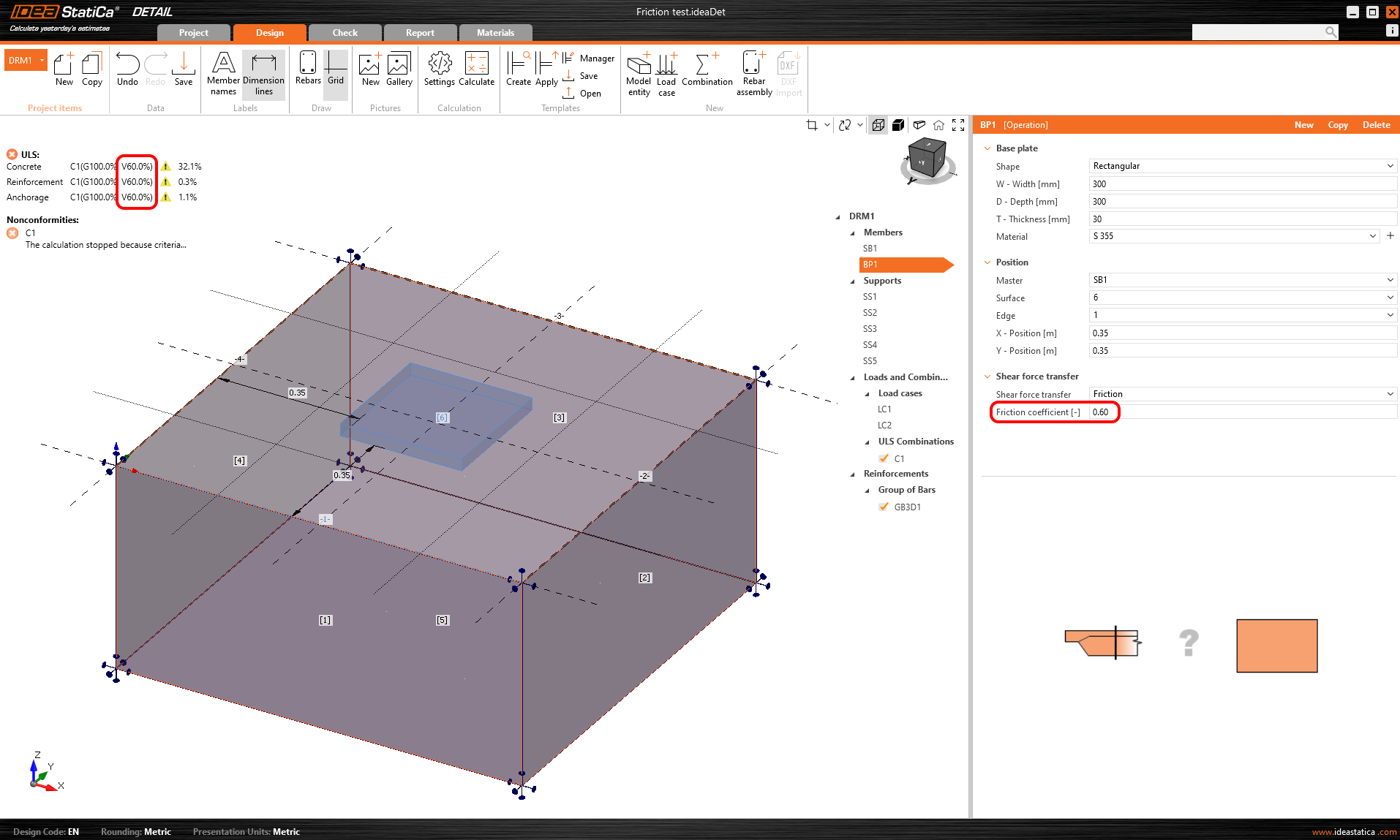
O coeficientede atrito deve ser introduzido como um valor projetado (calculado). No caso de a força de corte resultante Fxy exceder a força de pressão Fz vezes o coeficiente de atrito μ, o cálculo pára e nem todas as cargas se aplicam ao modelo. A condição é escrita da seguinte forma:
\[\frac {F_{xy}}{ \mu \cdot F_{z}}\le 1\]
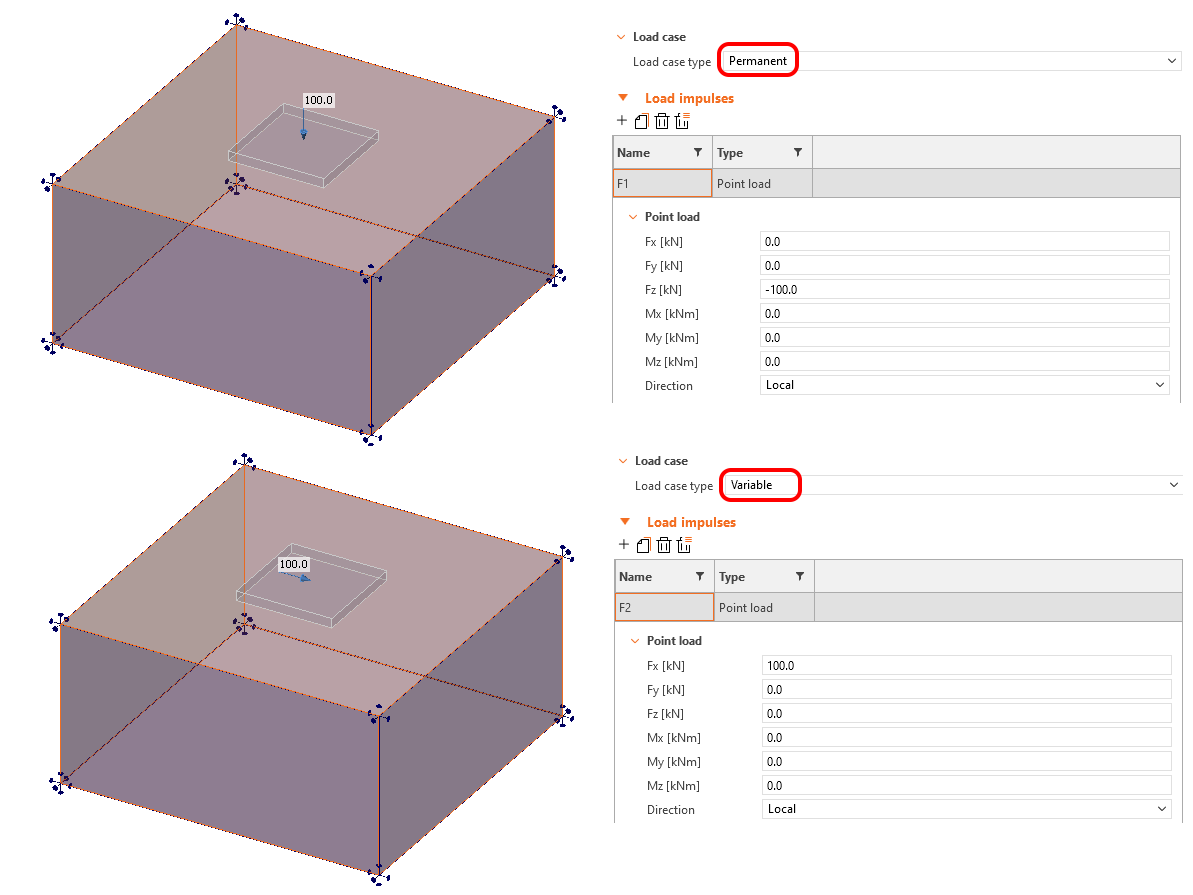
Isto pode ser visto no exemplo seguinte, onde são considerados dois casos de carga.
- LC1 - Tipo permanente - Fz = 100 kN
- LC2 - Tipo variável - Fx = 100 kN
\[ \textsf{\textit{\footnotesize{Fig. 14\qquad Entrada de carga para o exemplo que explica a transferência de corte por atrito}}}\]
No primeiro passo de cálculo, toda a carga permanente é aplicada. Em seguida, a carga variável é aplicada gradualmente até atingir o valor da carga de pressão vezes o coeficiente de atrito.
\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Resultados do exemplo que explica a transferência de corte por atrito}}}\]
O gráfico da Figura 16 define o comportamento do contacto de atrito entre a placa de base e o betão.
\[ \textsf{\textit{\footnotesize{Fig. 16\qquad Gráfico força-deslocamento que descreve o comportamento do contacto por atrito}}\]
O valor de Fzμ difere para cada incremento do cálculo, enquanto o valor da deformação de corte máxima uxy é constante.
Se a força normal de compressão Fz e a força de corte Fxy forem introduzidas num tipo de caso de carga (por exemplo, apenas permanente), e a condição de Fxy / (Fzμ) ≤ 1 não for cumprida, não será aplicada qualquer carga ao modelo porque a condição não é cumprida em nenhum incremento do cálculo.
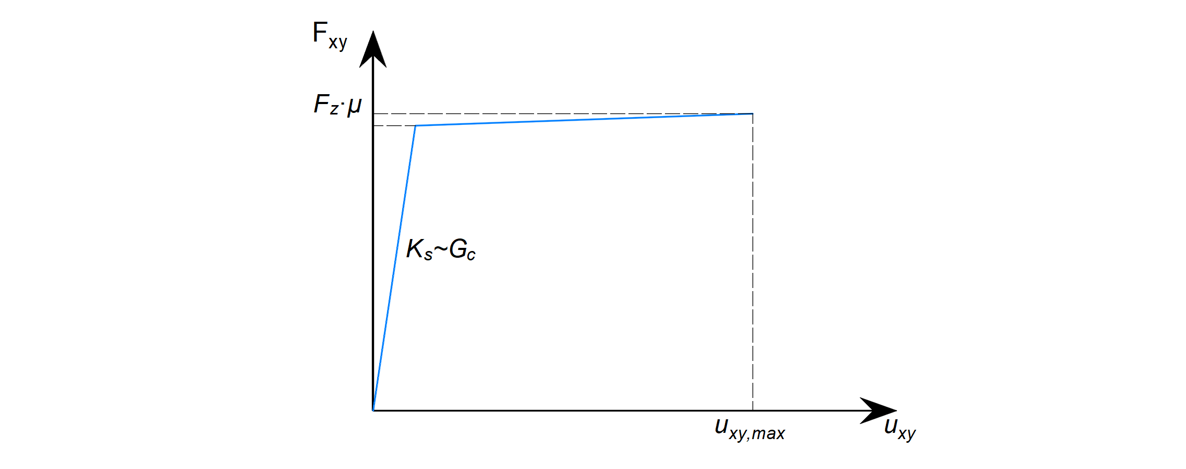
O olhal de corte está ligado à malha de betão por restrições que permitem apenas a compressão e a transferência de tensões normais.
\[ \textsf{\textit{\footnotesize{Fig. 17\qquad Shear lug transferência do mecanismo de corte}}}\]
O lug de cisalhamento é modelado a partir de elementos de casca lineares, onde o módulo de elasticidade E define o material.
Os resultados não são avaliados e apresentados para a placa de base, bem como para a barra de corte.
Ancoragens
Os elementos finitos que representam as ancoragens são modelados de forma a poderem transferir forças normais e de corte para o betão, tendo também em conta a rigidez à flexão das ancoragens. Para modelar o deslizamento entre a ancoragem e o betão circundante, são utilizados os mesmos elementos de ligação e MPC que para a armadura. A diferença é que, no caso das ancoragens adesivas, é possível especificar a resistência de projeto da ligação.
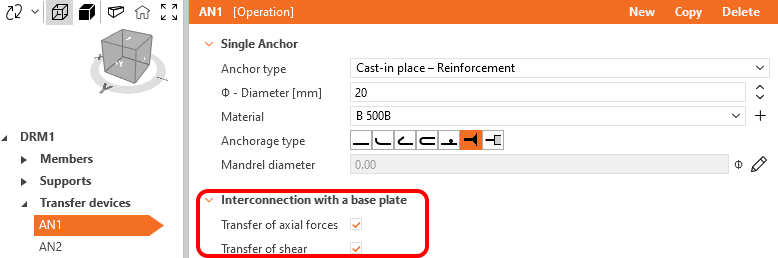
As ancoragens podem ser interligadas com placas de base. Para esta interligação, é utilizada uma restrição totalmente não linear para ligar a extremidade da ancoragem a um nó da placa de base. Este elemento permite-nos controlar todos os graus de liberdade para garantir, por exemplo, que nenhuma pressão é transferida pelas ancoragens para a placa de base sem separação, ou que nenhum corte é transferido pela ancoragem ao modelar um olhal de corte, etc.
As definições deinterligação com a placa de base para ancoragens permitem ao utilizador controlar se a ancoragem será ligada à placa de base através das restrições mencionadas anteriormente e como.
Na versão atual , apenas é suportado o contacto direto entre a placa de base e o betão .
A força de compressão não é transferida da placa de base para a ancoragem no caso de contacto direto. A compressão é transferida apenas pelo contacto entre a placa de base e o betão.
A caixa de verificação Transferência de forças axiais pode ser utilizada para controlar se a ancoragem e a placa de base serão ligadas ou não em termos de tensão. Isto é utilizado principalmente para a exportação da função Ligação (ver o capítulo correspondente). Para a modelação manual, faz sentido ter esta caixa de verificação sempre marcada.
A caixa de verificação Transferência de cisalhamento pode ser utilizada para controlar se a ancoragem e a placa de base serão ligadas ou não em termos de cisalhamento. Tenha em atenção que não é possível combinar mecanismos de transferência de corte, pelo que, para a transferência por fricção e por olhal de corte, esta caixa de verificação é irrelevante. Por outro lado, para a transferência de cisalhamento utilizando ancoragens, este campo dá a opção de excluir algumas ancoragens da transferência de cisalhamento.
Malha de betão em 3D CSFM
Os elementos finitos são implementados internamente e o modelo de análise é gerado automaticamente sem qualquer necessidade de interação com o utilizador. Uma parte importante deste processo é a criação de malhas.
Betão
Todos os elementos de betão são engrenados em conjunto. A aplicação calcula automaticamente um tamanho de elemento recomendado com base no tamanho e na forma da estrutura e tendo em conta o diâmetro do maior varão de reforço. Além disso, o tamanho de elemento recomendado garante que um mínimo de quatro elementos são gerados em partes finas da estrutura, tais como pilares delgados ou paredes finas, para assegurar resultados fiáveis nestas áreas. Os projectistas podem sempre selecionar um tamanho de elemento de betão definido pelo utilizador, modificando o multiplicador do tamanho de malha predefinido.
Armaduras
A armadura é dividida em elementos com aproximadamente o mesmo comprimento que o tamanho do elemento de betão. Uma vez geradas as malhas da armadura e do betão, estas são interligadas com elementos de ligação, como mostra a Fig. 9.
Refinamento
A malha de betão é automaticamente refinada sob a placa de base, em torno de ancoragens e em torno de olhais de cisalhamento. O tamanho da malha refinada é, por defeito, duas vezes mais pequeno do que a malha de betão básica. O raio da área refinada é definido como o tamanho do elemento multiplicado por dois.
O método de solução e o algoritmo de controlo de carga para CSFM 3D
É utilizado um algoritmo Newton-Raphson (NR) completo para encontrar a solução para um problema não linear do MEF.
Geralmente, o algoritmo NR não converge com frequência quando a carga total é aplicada num único passo. Uma abordagem habitual, que também é utilizada neste caso, consiste em aplicar a carga sequencialmente em vários incrementos e utilizar o resultado do incremento de carga anterior para iniciar a solução de Newton do incremento seguinte. Para este efeito, foi implementado um algoritmo de controlo da carga sobre o Newton-Raphson. No caso de as iterações NR não convergirem, o incremento de carga atual é reduzido para metade do seu valor e as iterações NR são repetidas.
Um segundo objetivo do algoritmo de controlo de carga é encontrar a carga crítica, que corresponde a determinados "critérios de paragem" - especificamente a deformação máxima no betão, o deslizamento máximo nos elementos de ligação, o deslocamento máximo nos elementos de ancoragem e a deformação máxima nos varões de reforço. A carga crítica é encontrada utilizando o método da bissecção. No caso de o critério de paragem ser excedido em qualquer parte do modelo, os resultados do último incremento de carga são descartados e é calculado um novo incremento com metade do tamanho do anterior. Este processo é repetido até que a carga crítica seja encontrada com uma certa tolerância de erro.
Para o betão, o critério de paragem foi definido para uma deformação de 5% em compressão (ou seja, cerca de uma ordem de grandeza superior à deformação de rotura real do betão) e 7% em tração nos pontos de integração dos elementos de casca. Na tração, o valor foi definido para permitir que a deformação limite na armadura, que é normalmente de cerca de 5% sem ter em conta o reforço da tração, seja atingida primeiro. Na compressão, o valor foi escolhido de entre várias alternativas como sendo suficientemente grande para que os efeitos do esmagamento sejam visíveis nos resultados, mas suficientemente pequeno para não causar demasiados problemas de estabilidade numérica.
\[ \textsf{\textit{\footnotesize{Fig 13\qquad Constitutive law of bond and anchorage elements used for anchorage length verification: a) Bond shear stress}}\] \[ \textsf{\textit{\footnotesize{resposta ao deslizamento do elemento de ligação, b) resposta força-deslocamento de um elemento de ancoragem}}}\]
Para o reforço, o critério de paragem é definido em termos de tensões. Uma vez que as tensões na fenda são modeladas, o critério em tensão corresponde à resistência à tração da armadura, tendo em conta o coeficiente de segurança. O mesmo valor é utilizado para o critério em compressão.
O critério de paragem nos elementos de ligação e nas molas de ancoragem é α-δumax, em que δumax é o deslizamento máximo utilizado nas verificações de código e α = 10.
Apresentação dos resultados 3D
Os resultados são apresentados de forma independente para o betão e para os elementos de armadura. Os valores de tensão e deformação no betão são calculados nos pontos de integração dos elementos de volume. No entanto, como não é prático apresentar os dados desta forma, os resultados são apresentados por defeito em nós, como o valor máximo da tensão de compressão a partir de pontos de integração de Gauss adjacentes em elementos ligados. É de notar que esta representação pode subestimar localmente os resultados nas extremidades comprimidas das barras num caso em que o tamanho do elemento finito é semelhante à profundidade da zona de compressão.
Os resultados para os elementos finitos de reforço são constantes para cada elemento (um valor - por exemplo, para tensões de aço) ou lineares (dois valores - para resultados de ligação). Para elementos auxiliares, tais como elementos de placas de apoio, apenas são apresentadas as deformações.
Modelo importado do IDEA StatiCa Connection
O modelo IDEA Statica Detail não tem de ser sempre modelado a partir do zero ou de um modelo. Existe também a opção de importar o modelo incluindo os efeitos de carga do IDEA StatiCa Connection. A geometria do bloco de betão, as ancoragens, a placa de base, os materiais e os efeitos de carga são transferidos.
\[ \textsf{\textit{\footnotesize{Fig. 16\qquad Cargas importadas do IDEA StatiCa Connection}}}\]
A placa de base é carregada por um grupo de forças determinado a partir da tensão geral de cada elemento finito das soldaduras que ligam a barra de aço e a placa de base.
Uma vez que a definição dos componentes individuais é diferente em Ligação e Detalhe (por exemplo, a placa de base é modelada por um material linear em Detalhe, enquanto que em Ligação é modelada por um material plástico), haveria uma redistribuição diferente de cargas entre o contacto placa de base-betão e as ancoragens, ou entre as próprias ancoragens. Por outras palavras, haveria diferentes forças normais de tração nas ancoragens em Ligação e Detalhe. Por esta razão, as ancoragens são importadas desligadas para forças normais (na direção da ancoragem) da placa de base, e as ancoragens são carregadas diretamente com as forças de tração aplicadas. Além disso, as forças opostas que carregam a placa de base localizada no local da ancoragem devem ser adicionadas para colocar o modelo em equilíbrio. Estas duas forças opostas são apresentadas na Figura 16.
No entanto, as forças de corte são transferidas pela interconexão da placa de base e da ancoragem (ou lug de corte, ou fricção). Este comportamento é possível porque existe uma restrição que liga a placa de base e a ancoragem, permitindo-nos controlar todos os graus de liberdade desta interligação.
Verificação do modelo
Estados limite
Estado limite último
As diferentes verificações exigidas por códigos de projeto específicos são avaliadas com base nos resultados diretos fornecidos pelo modelo. As verificações do estado limite último são efectuadas para a resistência do betão, a resistência das armaduras e a ancoragem (tensões de corte da ligação).
Para garantir que um elemento estrutural tem um dimensionamento eficiente, é altamente recomendável executar uma análise preliminar que tenha em conta os seguintes passos:
- Escolher uma seleção das combinações de cargas mais críticas.
- Calcular apenas as combinações de carga do estado limite último (ULS).
- Para acelerar o tempo de cálculo e resolver quaisquer problemas, considere a utilização de uma malha grosseira, aumentando o multiplicador do tamanho de malha predefinido na Configuração (Fig. 14). Se o modelo tiver um bom desempenho, reverta o multiplicador para um fator de 1.
\[ \textsf{\textit{\footnotesize{Fig 14\qquad Mesh multiplier}}}\]
Este modelo calcula muito rapidamente, permitindo aos projectistas rever a pormenorização do elemento estrutural de forma eficiente e executar novamente a análise até que todos os requisitos de verificação sejam cumpridos para as combinações de carga mais críticas. Uma vez cumpridos todos os requisitos de verificação desta análise preliminar, sugere-se a inclusão de todas as combinações de cargas últimas e a utilização de uma malha fina (a malha recomendada pelo programa). Os utilizadores podem alterar o tamanho da malha através do multiplicador, que pode atingir valores de 0,5 a 5 (Fig. 14).
Os resultados básicos e as verificações (tensão, deformação e utilização (i.e., o valor calculado/valor limite do código), bem como a direção das tensões principais no caso de elementos de betão) são apresentados através de diferentes gráficos onde a compressão é geralmente apresentada a vermelho e a tensão a azul. Os valores globais mínimos e máximos para toda a estrutura podem ser realçados, assim como os valores mínimos e máximos para cada parte definida pelo utilizador. Num separador separado do programa, podem ser apresentados resultados avançados tais como valores tensoriais, deformações da estrutura e relações de armadura (efectivas e geométricas) utilizadas para calcular o reforço de tração dos varões de reforço. Além disso, podem ser apresentadas cargas e reacções para combinações ou casos de carga selecionados.
Verificações estruturais de acordo com o EUROCODE
Modelos de materiais em 3D CSFM (EN)
Betão - ULS
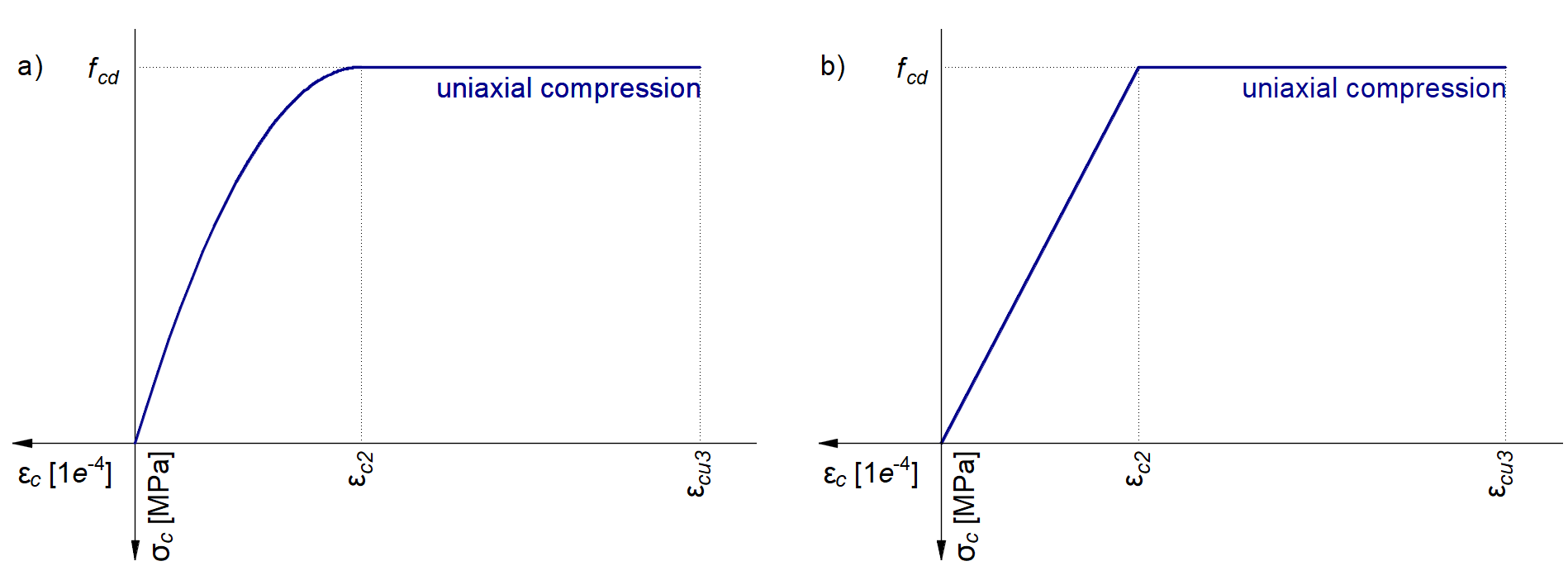
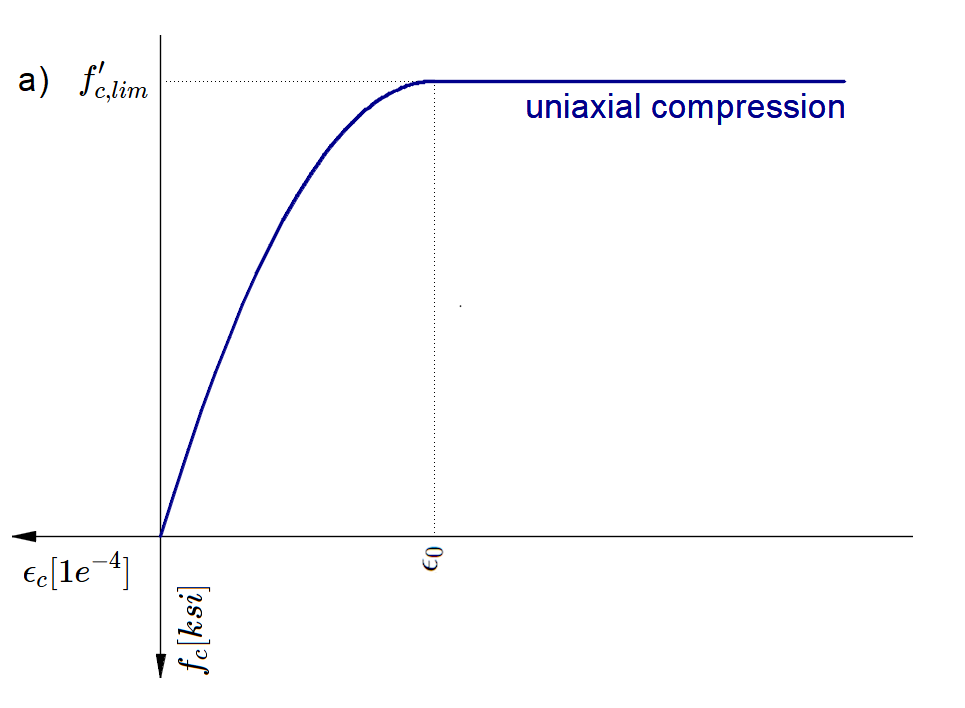
O modelo de betão implementado no 3D CSFM baseia-se nas leis constitutivas de compressão uniaxial prescritas pela EN 1992-1-1 para o dimensionamento de secções transversais, que apenas dependem da resistência à compressão. O diagrama parábola-retângulo especificado na norma EN 1992-1-1 Cl. 3.1.7 (1) (Fig. 15a) é utilizado por defeito no CSFM 3D, mas os projectistas podem também escolher uma relação elástica ideal plástica mais simplificada de acordo com a norma EN 1992-1-1 Cl. 3.1.7 (2) (Fig. 15b). A resistência à tração é negligenciada, tal como acontece no projeto clássico de betão armado.
\[ \textsf{\textit{\footnotesize{Fig 15\qquad Os diagramas tensão-deformação do betão para ULS: a) diagrama parábola-retângulo; b) diagrama bilinear}}}\]
A implementação do CSFM 3D no IDEA StatiCa Detail não considera um critério de rotura explícito em termos de deformações para o betão em compressão (ou seja, após a tensão de pico ser atingida, considera um ramo plástico com εcu2 (εcu3) num valor de 5% enquanto a EN 1992-1-1 assume uma deformação última inferior a 0,35%). Esta simplificação não permite verificar a capacidade de deformação das estruturas que falham à compressão. No entanto, a sua capacidade última fcd de acordo com a EN 1992-1-1 3.1.3 é corretamente prevista quando o aumento da fragilidade do betão à medida que a sua resistência aumenta é considerado através do fator de redução \ (\eta_{fc}\) definido no fib Model Code 2010 da seguinte forma:
\[f_{cd}={\alpha_{cc}} \cdot \frac{f_{ck,red}}{γ_c} = {\alpha_{cc}} \cdot \frac{\eta _{fc} \cdot f_{ck}}{γ_c}\]
\[{\eta _{fc}} = {\left( {\frac{{{30}}}{{{f_{ck}}}}} \right)^{\frac{1}{3}}} \le 1\]
onde:
αcc é o coeficiente que tem em conta os efeitos a longo prazo na resistência à compressão e os efeitos desfavoráveis resultantes da forma como a carga é aplicada. Está de acordo com a norma EN 1992-1-1 Cl. 3.1.6 (1). O valor por defeito é 1,0.
fck é a resistência caraterística do cilindro de betão (em MPa para a definição de \ ( \eta_{fc} \)).
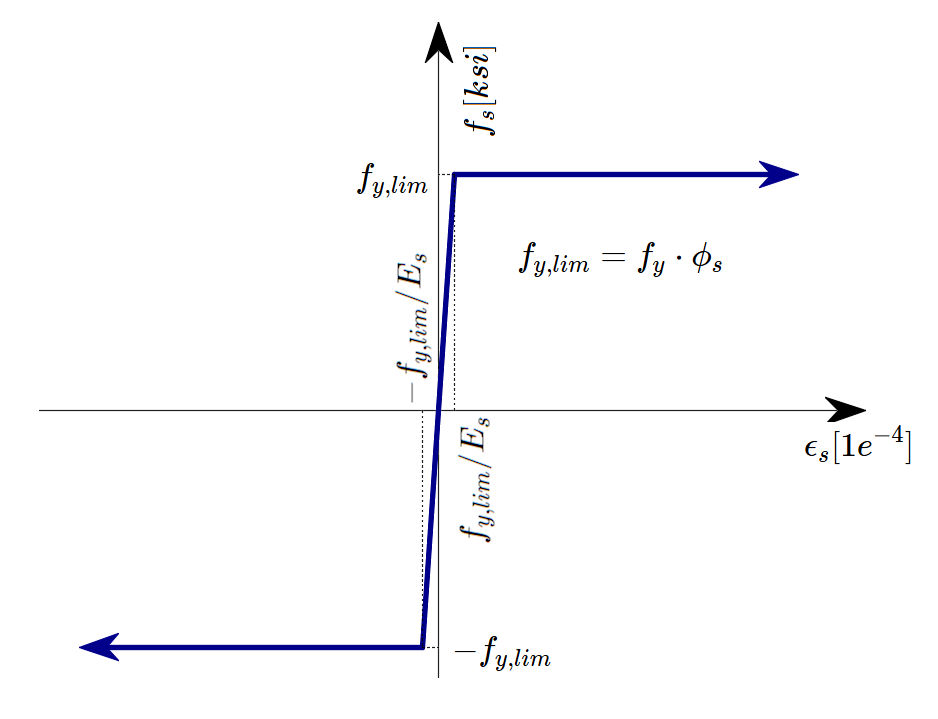
Reforço
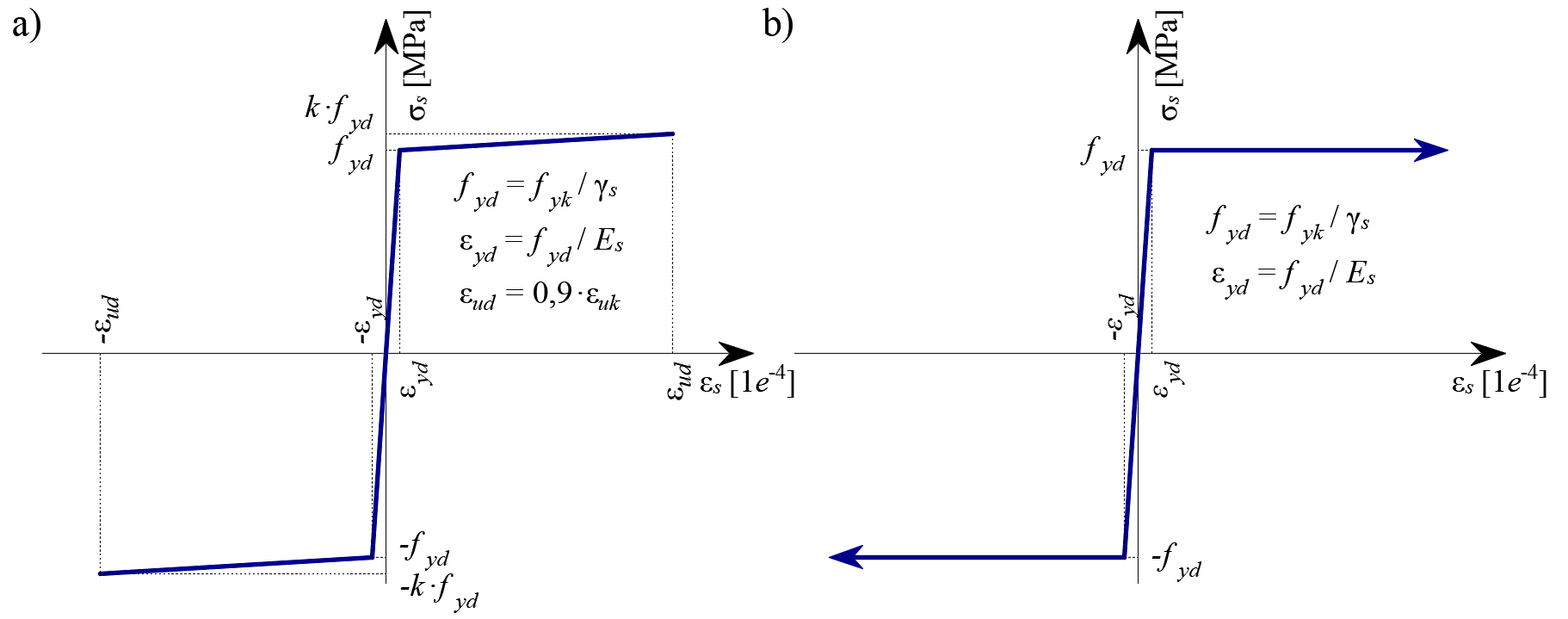
Por defeito, é considerado o diagrama tensão-deformação bilinear idealizado para os varões de reforço nus definido na EN 1992-1-1, secção 3.2.7 (Fig. 16). A definição deste diagrama requer apenas que as propriedades básicas da armadura sejam conhecidas durante a fase de projeto (classe de resistência e ductilidade). Sempre que conhecida, pode ser considerada a relação tensão-deformação efectiva da armadura (laminada a quente, trabalhada a frio, temperada e autotemperada, ...). O diagrama tensão-deformação da armadura pode ser definido pelo utilizador, mas, neste caso, é impossível assumir o efeito de enrijecimento por tração (é impossível calcular a largura da fenda). A utilização do diagrama tensão-deformação com um ramo superior horizontal não permite a verificação da durabilidade estrutural. Por isso, é necessária a verificação manual dos requisitos de ductilidade padrão.
\[ \textsf{\textit{\footnotesize{Fig. 16 \qquad Diagrama tensão-deformação da armadura: a) diagrama bilinear com um ramo superior inclinado; b) diagrama bilinear}}\] \[ \textsf{\textit{\footnotesize{com um ramo superior horizontal.}}}\]
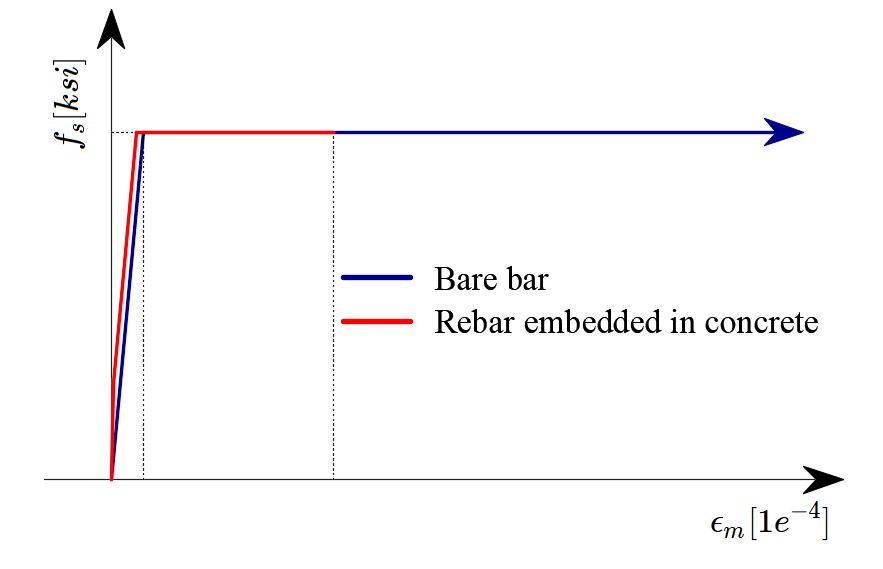
O reforço de tração (Fig. 17) é contabilizado automaticamente através da modificação da relação tensão-deformação de entrada do varão de armadura simples de forma a captar a rigidez média dos varões embebidos no betão (εm).
\[ \textsf{\textit{\footnotesize{Fig. 17\qquad Esquema de reforço de tensão.}}}\]
Factores de segurança parciais
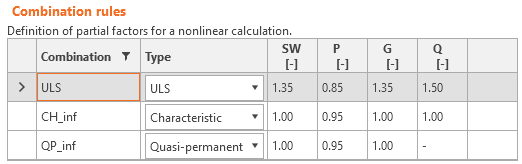
O Método do Campo de Tensões Compatível está em conformidade com as normas de projeto modernas. Uma vez que os modelos de cálculo utilizam apenas propriedades de material padrão, o formato do fator de segurança parcial prescrito nas normas de dimensionamento pode ser aplicado sem qualquer adaptação. Desta forma, as cargas de entrada são factorizadas e as propriedades caraterísticas do material são reduzidas utilizando os respectivos coeficientes de segurança prescritos nas normas de dimensionamento, exatamente como na análise convencional do betão. Os valores dos coeficientes de segurança dos materiais prescritos na EN 1992-1-1 cap. 2.4.2.4 são definidos por defeito, mas o utilizador pode alterar os coeficientes de segurança nas definições de Código e cálculo (Fig. 18).
\[ \textsf{\textit{\footnotesize{Fig. 18\qquad A configuração dos coeficientes de segurança dos materiais no Idea StatiCa Detail.}}}\]
Os coeficientes de segurança das cargas têm de ser definidos pelo utilizador em Regras de combinação para cada combinação não linear de casos de carga (Fig. 19). Para todos os modelos implementados no Idea StatiCa Detail, os coeficientes de segurança parciais já estão predefinidos.
\[ \textsf{\textit{\footnotesize{Fig. 19\qquad A definição dos factores parciais de carga em Idea StatiCa Detail.}}}\]
Utilizando combinações adequadas de coeficientes de segurança parciais definidas pelo utilizador, os utilizadores também podem calcular com o CSFM 3D utilizando o método do coeficiente de resistência global (Navrátil, et al. 2017), mas esta abordagem quase nunca é utilizada na prática de dimensionamento. Algumas orientações recomendam a utilização do método do fator de resistência global para análises não lineares. No entanto, em análises não lineares simplificadas (como o 3D CSFM), que apenas requerem as propriedades do material que são utilizadas em cálculos manuais convencionais, é ainda mais desejável utilizar o formato de segurança parcial.
Controlos de estado do limite máximo
As diferentes verificações exigidas pela norma EN 1992-1-1 são avaliadas com base nos resultados diretos fornecidos pelo modelo. As verificações ULS são efectuadas para a resistência do betão, a resistência das armaduras e a ancoragem (tensões de corte da ligação).
A resistência do betão à compressão é avaliada como o rácio entre a tensão principal equivalente máxima σc,eq obtida da análise de EF e o valor limite σc,lim = fcd.
A tensão principal equivalente expressa a tensão uni-axial equivalente para um estado de tensão tri-axial geral.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
O valor σc,eq pode, portanto, ser diretamente comparado com os limites de resistência uniaxial de acordo com 1992-1-1 Cl. 3.1.7 (1).
Esta expressão é derivada da implementação da teoria da plasticidade de Mohr-Coulomb, assumindo conservadoramente o ângulo de atrito interno φ = 0°.
A resistência da armadura é avaliada tanto em tração como em compressão como a relação entre a tensão na armadura nas fissuras σsr e o valor limite especificado σs,lim:
\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{para diagrama bilinear com ramo superior inclinado}}\)
\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\,\textsf{\small{para diagrama bilinear com ramo superior horizontal}}\)
em que:
fyk é a tensão de cedência da armadura de acordo com a norma EN 1992-1-1 Cl. 3.2.3,
k é o rácio entre a resistência à traçãoftk e a tensão de cedência,
\(k = \frac{f_{tk}}{f_{yk}}\)
γs é o fator de segurança parcial para o reforço.
A tensão de corte da ligação é avaliada independentemente como o rácio entre a tensão da ligação τb calculada pela análise de EF e a resistência final da ligação fbd, de acordo com a norma EN 1992-1-1 cap. 8.4.2:
\[\frac{τ_{b}}{f_{bd}}\le 1\]
\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]
em que:
fctd é o valor de projeto da resistência à tração do betão de acordo com a norma EN 1992-1-1 Cl. 3.1.6 (2). Devido à fragilidade crescente do betão de resistência mais elevada, fctk,0.05 é limitado ao valor para C60/75 de acordo com a norma EN 1992-1-1 Cl. 8.4.2 (2)
η1 é um coeficiente relacionado com a qualidade da condição de ligação e a posição da barra durante a betonagem (Fig. 31).
η1 = 1,0 quando se obtêm "boas" condições e
η1 = 0,7 para todos os outros casos e para barras em elementos estruturais construídos com formas deslizantes, a menos que se possa demonstrar que existem "boas" condições de ligação
η2 está relacionado com o diâmetro da barra:
η2 = 1,0 para Ø ≤ 32 mm
η2 = (132 - Ø)/100 para Ø > 32 mm
\[ \textsf{\textit{\footnotesize{Fig. 20\qquad EN 1992-1-1 Figura 8.2 - Descrição das condições de ligação.}}}\]
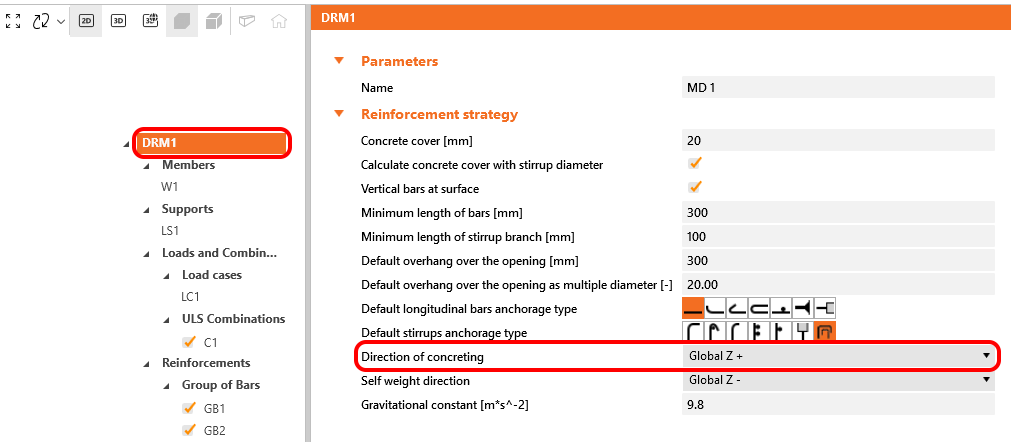
No IDEA StatiCa Detail, as condições de ligação são tidas em conta de acordo com a Fig. 20 c) e d). A direção da betonagem pode ser definida na aplicação para cada item do projeto da seguinte forma:
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad Direção de betonagem}}}\]
Estas verificações são efectuadas em relação aos valores-limite apropriados para as respectivas partes da estrutura (isto é, apesar de haver uma única classe para o betão e para o material de reforço, os diagramas finais de tensão-deformação serão diferentes em cada parte da estrutura devido aos efeitos de enrijecimento por tração e amolecimento por compressão).
Força total Ftot e força limite Flim
A força total Ftot é o resultado da análise de elementos finitos e pode ser definida de duas formas.
\[F_{tot}=A_{s}\cdot \sigma_{s}\]
ondeAs é a área da barra de reforço e σs é a tensão na barra.
Ou como uma soma da força de ancoragemFa e da força de ligação Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
em queFa é a força real na mola de ancoragem e Fbond é a força de ligação que pode ser obtida através da integração da tensão de ligação τb ao longo do comprimento da barra de reforço l.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs é a circunferência do varão de reforço.
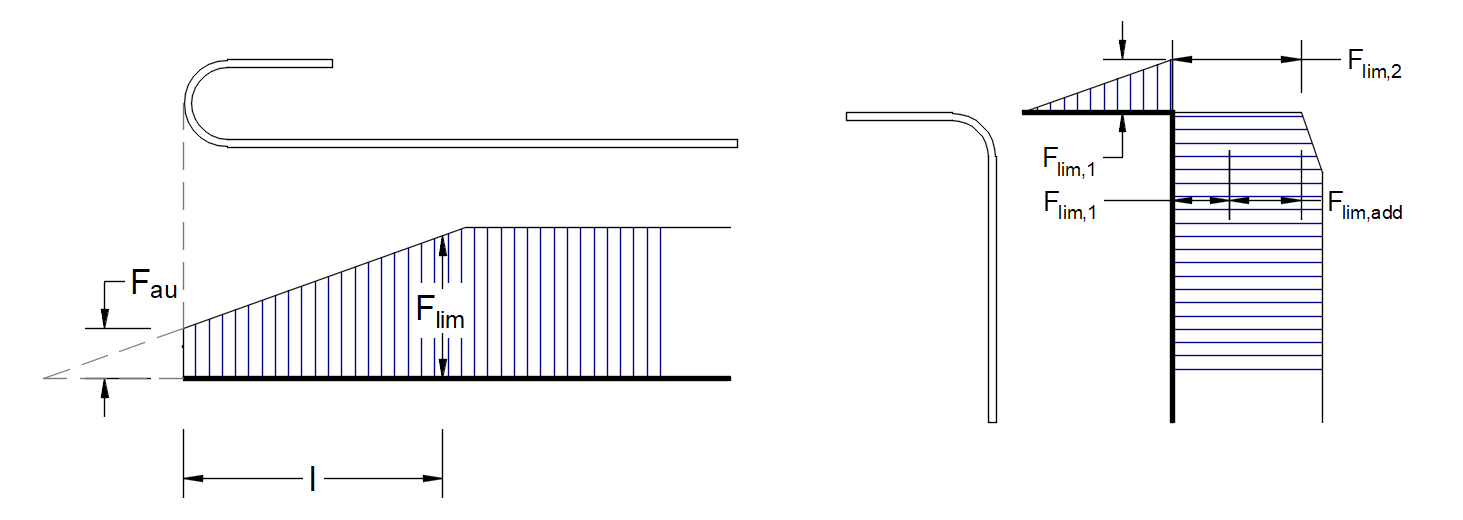
A força limiteFlim é a força máxima no elemento do varão considerando a resistência última do varão e também as condições de ancoragem (ligação entre o betão e a armadura e ganchos de ancoragem, laços, etc.).
\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]
\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]
\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]
\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]
em que Cs é a circunferência da barra de reforço e l é o comprimento desde o início da barra de reforço até ao ponto de interesse.
\[ \textsf{\textit{\footnotesize{Fig. 22\qquad Definição da força limite Flim}}\]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
em queFlim,add é a força adicional calculada a partir da magnitude do ângulo entre elementos vizinhos.Flim,2 deve ser sempre inferior aFu.
Os tipos de ancoragem disponíveis no CSFM 3D incluem uma barra reta (i.e., sem redução da extremidade da ancoragem), curva, gancho, laço, barra transversal soldada, ligação perfeita e barra contínua. Todos estes tipos, juntamente com os respectivos coeficientes de ancoragem β, são apresentados na Fig. 23 para a armadura longitudinal e na Fig. 24 para os estribos. Os valores dos coeficientes de ancoragem adoptados estão de acordo com a norma EN 1992-1-1, secção 8.4.4 Tab. 8.2. É de notar que, apesar das diferentes opções disponíveis, o CSFM 3D distingue três tipos de extremidades de ancoragem: (i) nenhuma redução no comprimento da ancoragem, (ii) uma redução de 30% do comprimento da ancoragem no caso de uma ancoragem normalizada, e (iii) ligação perfeita.
\[ \textsf{\textit{\footnotesize{Fig. 23\qquad Tipos de ancoragem disponíveis e respetivos coeficientes de ancoragem para varões de reforço longitudinal no CSFM 3D:}}}\]
\[ \textsf{\textit{\footnotesize{(a) varão reto; (b) dobra; (c) gancho; (d) laço; (e) varão transversal soldado; (f) ligação perfeita; (g) varão contínuo.}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 24\qquad Tipos de ancoragem disponíveis e respectivos coeficientes de ancoragem para estribos.}}}\]
\[ \textsf{\textit{\footnotesize{Estribos fechados: (a) gancho; (b) dobra; (c) sobreposição. Estribos abertos: (d) gancho; (e) barra contínua.}}}\]
Para cumprir a norma EN 1992-1-1, a mola de ancoragem deve ser utilizada no cálculo, a mola de ancoragem é modificada pelo coeficiente β, pelo que o utilizador deve utilizar um dos tipos de ancoragem disponíveis ao definir as condições de início e fim da armadura.
Verificações estruturais de acordo com ACI 318-19
O CSFM 3D está em conformidade com o ACI 318-19, capítulo 6.8.1.1. Para que o CSFM 3D cumpra os requisitos da secção 6.8.1.2 do ACI 318-19, foram efectuados muitos testes de verificação em várias universidades. Os artigos individuais que resumem os resultados da verificação e validação podem ser encontrados na seguinte hiperligação.
Modelos de materiais em 3D CSFM (ACI)
Betão - Resistência
O modelo de betão implementado para o cálculo da resistência no CSFM baseia-se na curva tensão-deformação parabólica-plástica para o betão baseada na curva tensão-deformação parabólica da Portland CementAssociation descrita nas Notas da PCA sobre os requisitos do código de construção ACI 318-99 para betão estrutural, Figura 6-8. A resistência à tração é negligenciada, tal como acontece no projeto clássico de betão armado.
\[ \textsf{\textit{\footnotesize{Fig. 38\qquad O diagrama tensão-deformação do betão para análise de resistência}}}\]
A implementação do CSFM no IDEA StatiCa Detail não considera um critério de rotura explícito em termos de deformações para o betão à compressão (ou seja, após a tensão de pico ser atingida, considera um ramo plástico com εc0 no valor máximo de 5%, enquanto o ACI 318-19 Cl. 22.2.2.1 assume uma deformação final inferior a 0,3%). Esta simplificação não permite verificar a capacidade de deformação das estruturas que falham à compressão. No entanto, a resistência é corretamente prevista quando se considera o aumento da fragilidade do betão à medida que a sua resistência aumenta, através do fator de redução \ (\eta_{fc}\) definido no fib Model Code 2010 da seguinte forma:
\[f'_{c,lim}=\alpha_{1}\cdot\phi_{c}\cdot \eta _{fc}\cdot f'_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{{30}}}{{{f'_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
em que:
α1 é o fator de redução da resistência à compressão do betão definido no ACI 318-19 Cl. 22.2.2.4.1. Quando se utiliza um diagrama tensão-deformação parábola-retângulo, é necessário reduzir a tensão de compressão máxima por este fator. Isto faz com que a distribuição de tensões na zona de compressão seja a média, de modo a que a resistência à compressão resultante seja menor ou igual à resistência à compressão calculada utilizando um diagrama tensão-deformação com um ramo plástico decrescente.
Φcé o fator de redução da resistência do betão. O valor por defeito é definido de acordo com a Tabela 24.2.1 (b)(f) do ACI 318-19.
f'c é a resistência do cilindro de betão (em MPa para a definição de \ ( \eta_{fc} \)).
Reforço
Considera-se um diagrama tensão-deformação perfeitamente elasto-plástico com um ponto de cedência definido para a armadura sem pré-esforço. Ver ACI 319-19 CL. 20.2.1. A definição deste diagrama requer apenas que as propriedades básicas da armadura sejam conhecidas - resistência e módulo de elasticidade.
O diagrama tensão-deformação da armadura também pode ser definido pelo utilizador, mas, neste caso, é impossível assumir o efeito de rigidez à tração.
\[ \textsf{\textit{\footnotesize{Fig. 42 \qquad Diagrama tensão-deformação do reforço}}}\]
onde:
Φsé o fator de redução de resistência para o reforço. Onde o valor predefinido é definido de acordo com a Tabela 24.2.1 do ACI 318-19.
fy é a tensão de cedência da armadura
Es módulo de elasticidade da armadura
10% é selecionado como a deformação limite na qual o cálculo é interrompido. Este valor é considerado seguro com base no artigo 7 da norma ASTM A955/A955M-20c.
A rigidez à tração (Fig. 43) é contabilizada automaticamente através da modificação da relação tensão-deformação de entrada do varão de reforço nu, de modo a captar a rigidez média dos varões embebidos no betão (εm).
\[ \textsf{\textit{\footnotesize{Fig. 43\qquad Esquema de reforço de tensão.}}}\]
Verificações e validações
Referências
- Wu, D.; Wang, Y.; Qiu, Y.; Zhang, J.; Wan, Y.-K. Determinação dos parâmetros de Mohr-Coulomb a partir de critérios de resistência não lineares para taludes 3D. Math. Probl. Eng. 2019, 6927654.
- Lelovic, S.; Vasovic, D.; Stojic, D. Determinação dos parâmetros de material de Mohr-Coulomb para concreto sob teste de tração indireta. Tech. Gaz. 2019, 26, 412-419.
- Galic, M.; Marovic, P.; Nikolic, Ž. Modelo de material Mohr-Coulomb-Rankine modificado para concreto. eng. Comput. 2011, 28, 853-887.
- Fan, Q.; Gu, SC; Wang, BN; Huang, RB Critério de Força Parabólica de Mohr de Dois Parâmetros Aplicado para Analisar os Resultados do Teste Brasileiro. Aplicar. Mech. Mater. 2014, 624, 630-634.