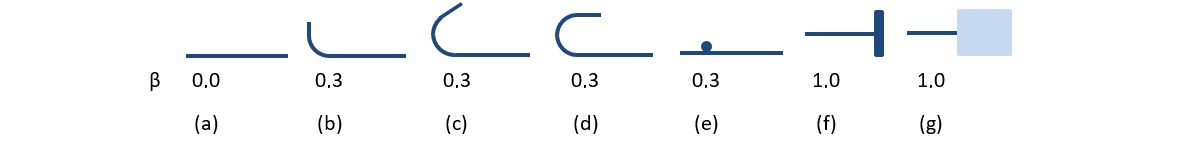In der Praxis stoßen Ingenieure auf verschiedene Arten von finiten Elementen (von einfachen 1D-Stabelementen bis hin zu komplizierteren 3D-Volumenelementen), die in einer Vielzahl von Anwendungen für die Analyse von Baukonstruktionen verwendet werden. Ein gemeinsames Merkmal der linearen Analyse liegt zweifellos in ihrer Schnelligkeit, Übersichtlichkeit und in der Tatsache, dass diese Lösung für eine Vielzahl von Problemen völlig ausreichend ist.

Vor allem bei Betonkonstruktionen kommt es häufig vor, dass der lineare Ansatz nicht ausreicht, weil nach dem Auftreten der ersten Risse im belasteten Element die Spannungen umverteilt werden und das Problem deutlich nichtlinearer wird.

Aus diesem Grund hat IDEA StatiCa die 3D-CSFM (Compatible Stress Field Method) entwickelt und in der Detail-Anwendung durch den Einsatz von Volumenelementen umgesetzt. 3D CSFM erweitert die etablierte CSFM in eine dritte Dimension und bietet eine schnelle und normgerechte Lösung, die vor allem für den Alltagsingenieur anwendbar ist und ihm eine einzigartige neue Möglichkeit bietet, die komplexen Details von Betonstrukturen sicher zu bewältigen.

Wichtigste Annahmen und Einschränkungen

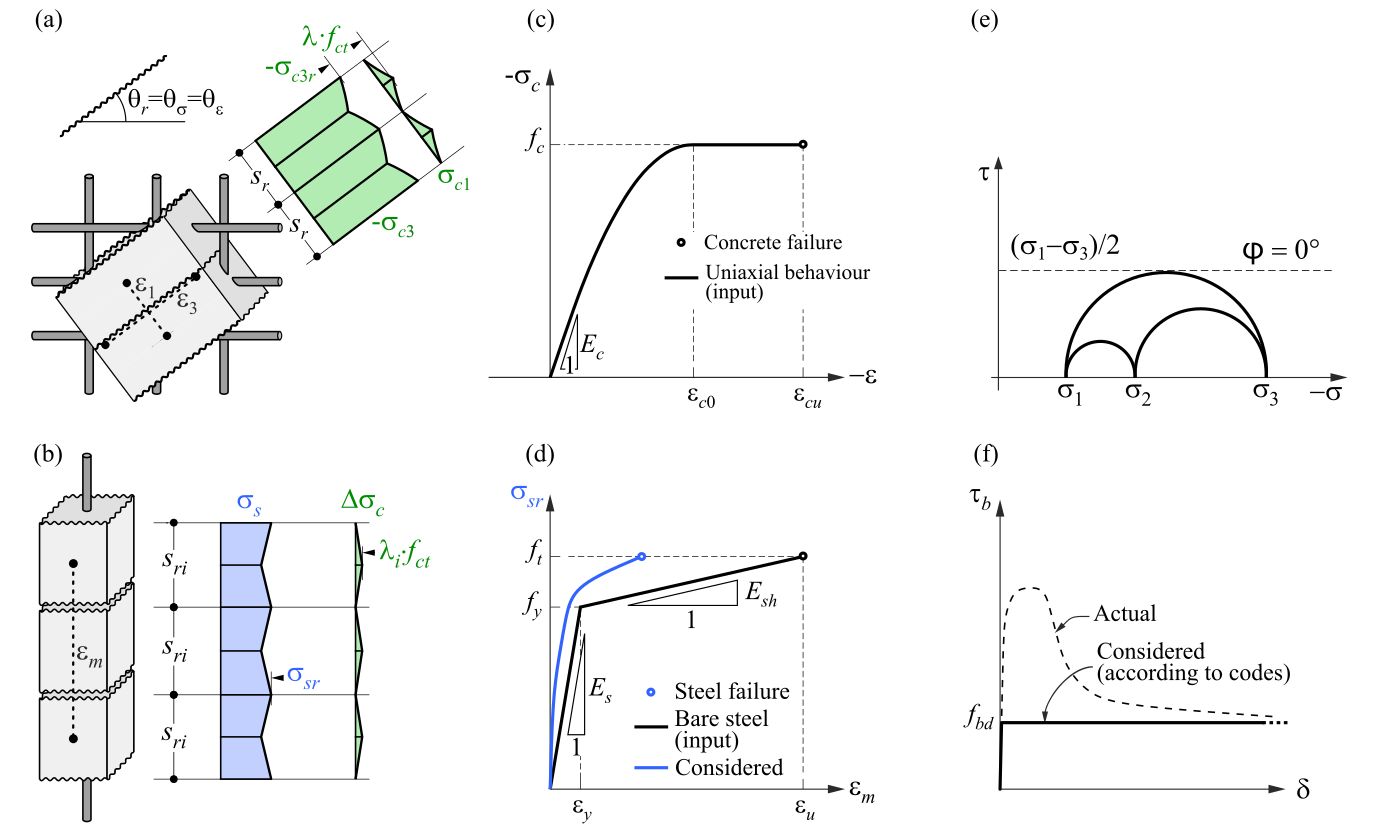
3D CSFM definiert das Betonverhalten auf der Grundlage der modifizierten Mohr-Coulomb-Plastizitätstheorie für monotone Belastung. Die Methode berücksichtigt die Hauptdruckspannungen des Betons und die Betonstahlspannungen (σ_sr) an den Rissen und vernachlässigt die Zugfestigkeit des Betons, mit Ausnahme der Mitwirkung des Beton Zwischen den Rissen (Zugaussteifung).

σ_c1r, σ_c2r, σ_c3r ≤ 0 MPa

Die Bewehrungsstäbe sind mit den finiten Elementen des Betonvolumens durch Verbundelemente verbunden, die ein Gleiten zwischen Beton und Bewehrung ermöglichen. Es ist zu beachten, dass die 3D-CSFM nicht für die Simulation von unbewehrtem Beton geeignet ist. Im Allgemeinen umfasst die Mohr-Coulomb-Theorie zwei grundlegende Eigenschaften, die die Entwicklung der Plastizitätsfläche unter Druck und teilweise unter Zug bestimmen: den inneren Reibungswinkel φ und den Kohäsionsparameter c. 3D CSFM geht von einem inneren Reibungswinkel von Null aus (Abb. 1e), was zu einer konservativen Bemessung führt.

\( \textsf{\textit{\footnotesize{Abb. 1\qquad Grundannahmen des 3D CSFM: (a) Hauptspannungen im Beton; (b) Spannungen in Bewehrungsrichtung;}}}\) \( \textsf{\textit{\footnotesize{(c) Spannungs-Dehnungs-Diagramm des Betons in Form von maximalen Spannungen; (d) Spannungs-Dehnungs-Diagramm}}}\) \( \textsf{\textit{\footnotesize{des Betonstahls in Form von Spannungen an Rissen und mittleren Dehnungen; (e) Mohrsche Kreise für Betonmodell in 3D CSFM; }}}\) \( \textsf{\textit{\footnotesize{(f) Verbund Schubspannung-Schlupf-Beziehung für Verankerungslängennachweise.}}}\)

Beton

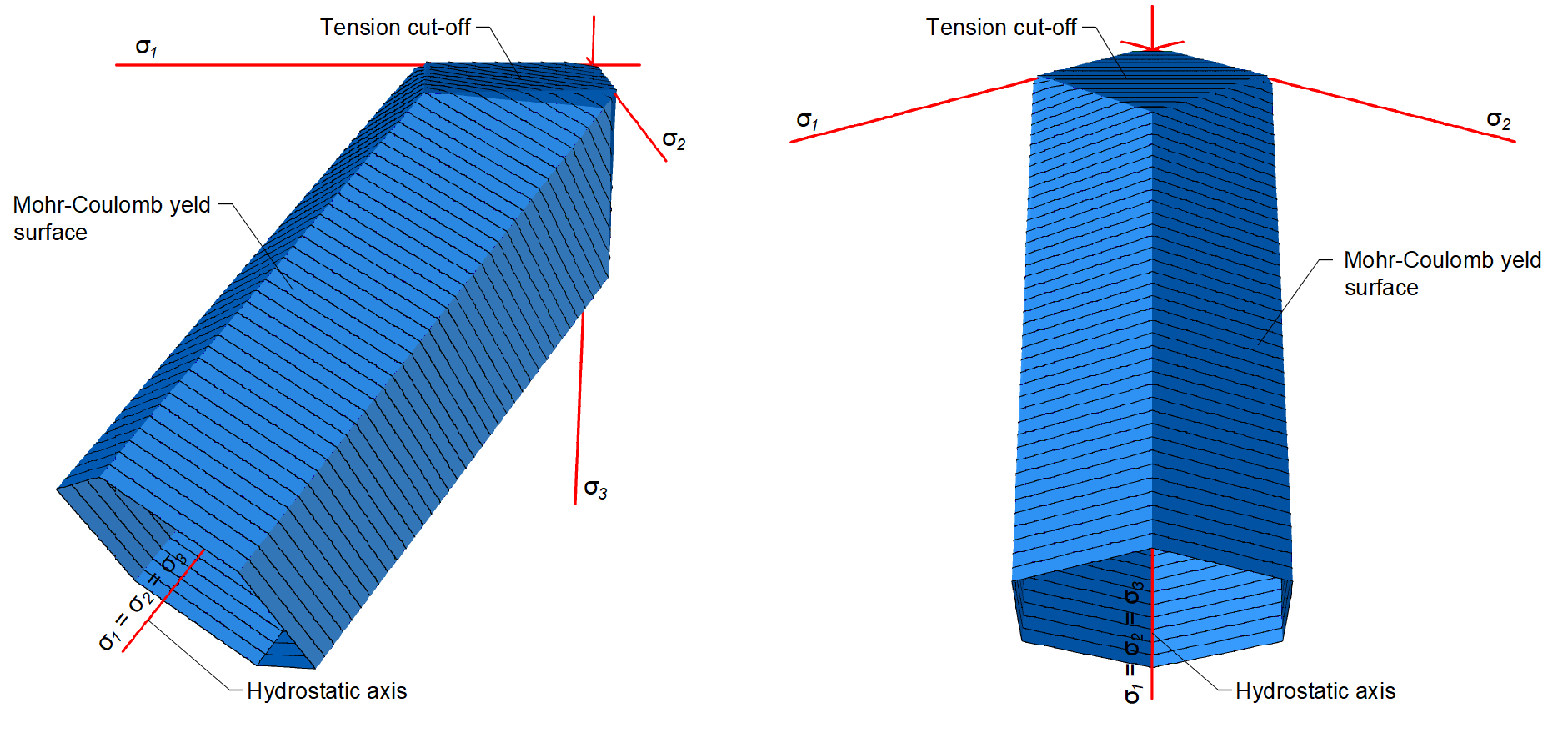
Das vorgestellte Materialmodell ist ein Mehrflächenplastizitätsmodell, das durch die Kombination des Mohr-Coloumb- und des Rankine-Modells für monotone Belastung gegeben ist. Es ist wichtig zu beachten, dass dieses Modell keine Entlastung berücksichtigt, wie es bei klassischen Plastizitätsmodellen für zyklische Belastung der Fall wäre.

\[ \textsf{\textit{\footnotesize{Abb. 2\qquad Mohr-Coulomb-Mehrflächenplastizitätsmodell für den Reibungswinkel 0 Grad}}}\]

Wie bereits erwähnt, ist das Materialmodell für Anwendungen von bewehrtem Beton gedacht. Dies ist auf die Vernachlässigung von Beton unter Zug zurückzuführen. Daher ist das Modell nicht einmal für Bauteile geeignet, bei denen die Bemessungsregeln für Stahlbeton, wie Mindestbewehrungsgrad, maximaler Stababstand usw., nicht erfüllt sind. Es sollte auch hinzugefügt werden, dass aus Gründen der numerischen Stabilität eine sehr kleine Zugkapazität im Modell definiert ist. Der Zugteil wird durch Ebenen begrenzt, die dem Rankine-Modell entsprechen.

3D CSFM in IDEA StatiCa Detail berücksichtigt kein explizites Versagenskriterium in Form von Dehnungen für Beton unter Druck (d.h. es wird ein unendlich plastischer Zweig nach Erreichen der Spitzenspannung betrachtet). Durch diese Vereinfachung kann die Verformungskapazität von Bauwerken, die auf Druck versagen, nicht nachgewiesen werden. Ihre Tragfähigkeit wird jedoch richtig vorhergesagt, wenn die Zunahme der Sprödigkeit des Betons bei steigender Festigkeit mit Hilfe des im fib Model Code 2010 wie folgt definierten Abminderungsfaktors 𝜂_𝑓𝑐 berücksichtigt wird:

\[f_{c,red} = \eta _{fc} \cdot f_{c}\]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]

wobei:

f_c die charakteristische Festigkeit des Betonzylinders ist (in MPa für die Definition von \ ( \eta_{fc} \)).

f_c,red wird dann mit der äquivalenten Hauptspannung σ_c_,eq im Beton verglichen, die natürlich unter Berücksichtigung aller in den Normen vorgeschriebenen Sicherheitsfaktoren weiter definiert wird.

Eine detaillierte Beschreibung des Betonmodells finden Sie unter dem folgenden Link:

Betonmaterialmodell für 3D-Detail

Bewehrung

Das bilineare Spannungs-Dehnungs-Diagramm für Bewehrungsstäbe, wie es in den Bemessungsregeln definiert ist (Abb. 1d), stellt ein idealisiertes Modell dar. Dieses Modell setzt die Kenntnis der grundlegenden Eigenschaften der Bewehrung während der Bemessungsphase voraus, insbesondere der Festigkeits- und Duktilitätsklasse. Alternativ kann der Anwender auch eine individuelle Spannungs-Dehnungs-Beziehung definieren.

Die Mitwirkung des Betons zwischen den Rissen (Tension Stiffening) wird berücksichtigt, indem die Spannungs-Dehnungs-Beziehung des "nackten" Bewehrungsstabs modifiziert wird, um die durchschnittliche Steifigkeit der im Beton eingebetteten Stäbe (ε_m) zu erfassen (Abb. 1b).

Verankerung

Der Verbundschlupf zwischen der Bewehrung und dem Beton wird in das Finite-Elemente-Modell aufgenommen, indem die vereinfachte starr-perfektplastische Beziehung in (Abb. 1f) berücksichtigt wird, wobei f_bd der Bemessungswert (faktorisierter Wert) der Verbundspannung ist, der in der Bemessungsvorschrift für die spezifischen Verbundbedingungen angegeben ist.

Es handelt sich hierbei um ein vereinfachtes Modell, das ausschließlich dem Zweck dient, die in den Bemessungsvorschriften vorgeschriebenen Verbundspannungen (d. h. die Verankerung der Bewehrung) zu berücksichitgen. Die Reduzierung der Verankerungslänge bei der Verwendung von Haken, Schlaufen und ähnlichen Stabformen kann durch die Definition einer bestimmten Kapazität am Ende der Bewehrung berücksichtigt werden, wie weiter unten beschrieben wird.

Verankerungen

Das Ankerelement ist so definiert, dass es sowohl normale Zug- oder Druckkräfte als auch Querkräfte übertragen kann, wobei auch die Biegesteifigkeit der Anker berücksichtigt wird. Es wird jedoch nur die Normalspannung in den Ankern bewertet.

Es gibt zwei Arten von Ankern:

Chemische Anker
Betonstahlanker

Die Betonstahlanker verhalten sich wie die klassische Bewehrung (Verankerungsart, Verbund, usw.). Bei chemischen Ankern kann der Bemessungswert Verbundfestigkeit direkt definiert werden. Dieser Wert sollte aus dem technischen Datenblatt des Herstellers bzw. Zulassung entnommen werden.

Umsetzung der Mohr-Coulomb-Plastizitätstheorie in 3D CSFM

Im folgenden Kapitel wird dargestellt, wie die Mohr-Coulomb-Theorie in 3D CSFM umgesetzt wird. Wir erläutern, wie die Umschnürungswirkung (dreiachsige Spannung) berücksichtigt wird und wie die äquivalente Hauptspannung σ_c_,eq berechnet wird, die zur Bestimmung der Tragfähigkeit aus Sicht des Betons verwendet wird.

Einführung in die Theorie

Die Mohr-Coulomb-Theorie ist ein mathematisches Modell, das das Verhalten von spröden Materialien auf Schub- und Normalspannungen beschreibt. Die meisten klassischen technischen Werkstoffe folgen dieser Regel zumindest in einem Teil ihres Schubbruchbereichs. Im Allgemeinen gilt die Theorie für Materialien, bei denen die Druckfestigkeit die Zugfestigkeit bei weitem übersteigt z.B. Beton.

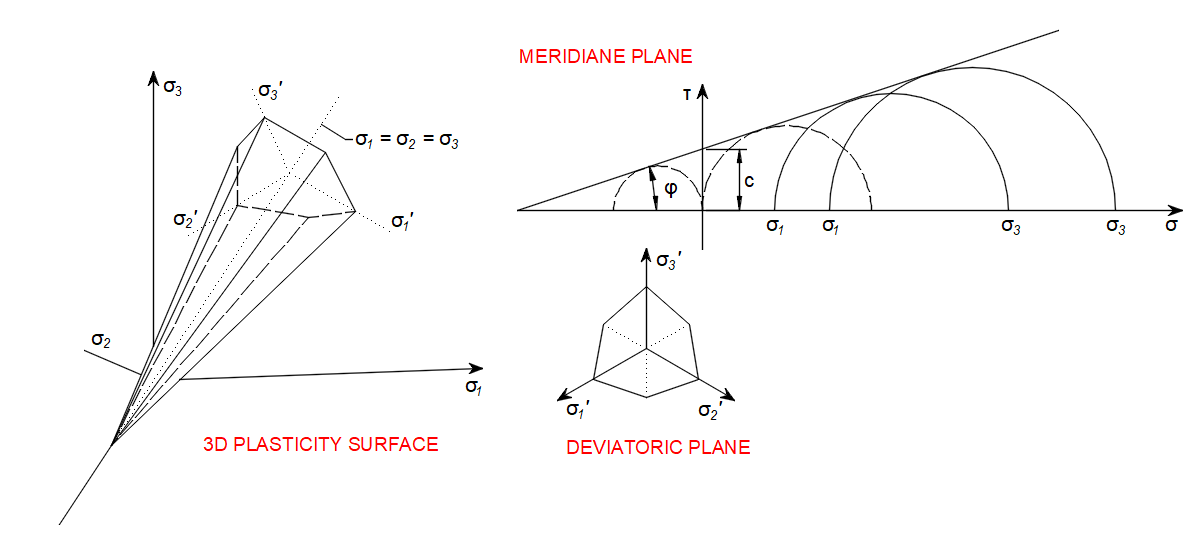
\[ \textsf{\textit{\footnotesize{Abb. 3\qquad Mohr-Coulomb-Plastizitätsmodell}}}\]

Im Bauwesen wird dieses Model zur Bestimmung der Bruchlast verwendet. Mit Hilfe der Coulomb'schen Reibungshypothese wird die Kombination von Schub- und Normalspannung bestimmt, die einen Bruch des Materials verursacht, und mit Hilfe des Mohr'schen Kreises wird ermittelt, welche Hauptspannungen diese Kombination von Scher- und Normalspannung hervorrufen und in welchem Winkel der Ebene dies geschieht.

\[ \textsf{\textit{\footnotesize{Abb. 4\qquad Meridianebene und Spannungsschnitt}}}\]

Es kann gezeigt werden, dass bei einem Material, das nach der Coulombschen Reibungshypothese versagt, die beim Versagen eingeleitete Verschiebung einen Winkel zur Bruchlinie bildet, der dem Reibungswinkel entspricht. Dadurch lässt sich die Festigkeit des Werkstoffs durch den Vergleich der durch die Verschiebung und die äußere Belastung eingebrachten äußeren mechanischen Arbeit mit der durch die Dehnung und die Spannung an der Bruchlinie eingebrachten inneren mechanischen Arbeit bestimmen. Aufgrund der Energieerhaltung muss die Summe dieser Arbeiten gleich Null sein, was die Berechnung der Bruchlast der Konstruktion ermöglicht.

Umsetzung in 3D CSFM

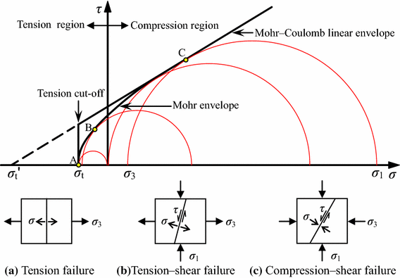
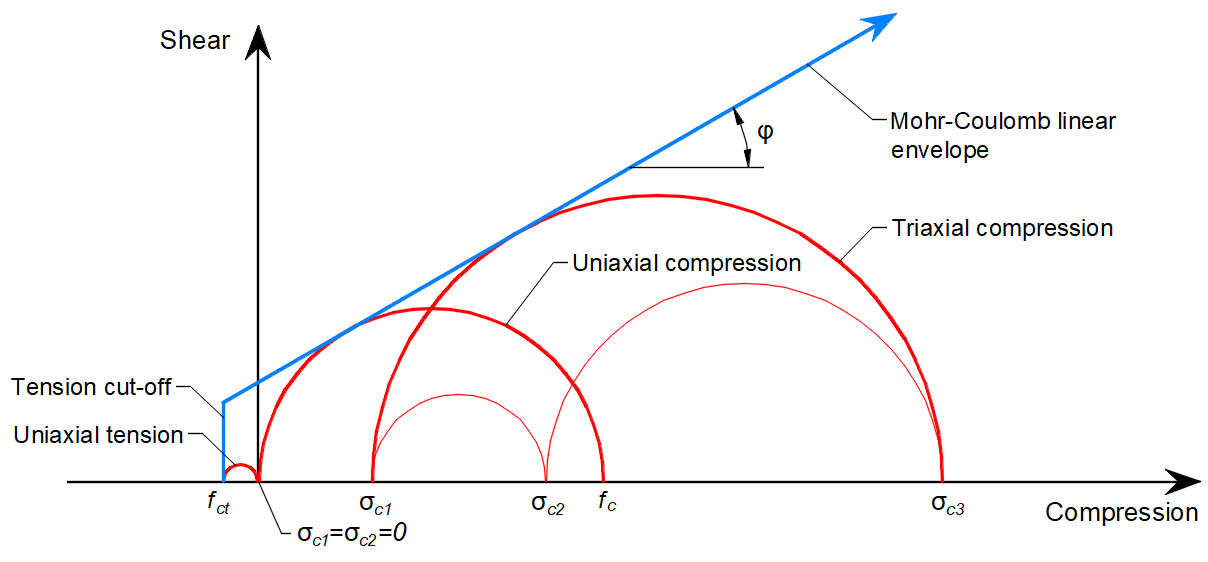
Im Allgemeinen können für einen gegebenen inneren Reibungswinkel des Betons, der in den Referenzen [1], [2], [3], [4] bei etwa φ = 30-40° liegt, die Zug- und Druckfestigkeiten der Mohr'schen Kreise des Betons wie in Abbildung 5 dargestellt werden.

\[ \textsf{\textit{\footnotesize{Abb. 5\qquad Mohr'sche Kreise für Beton}}}\]

Dabei ist f_c die Druckfestigkeit des Betons, f_ct die Zugfestigkeit des Betons, φ der innere Reibungswinkel und σ_c1, σ_c3 die Hauptspannungen des Betons unter dreiachsigem Druck.

Es ist festzustellen, dass mit zunehmender Hauptspannung σ_c3 auch die maximal mögliche Differenz zwischen den Werten von σ_c3 und σ_c1, die wir als maximale σ_c_,eq definieren (siehe unten), zunimmt. Diese Differenz entspricht dem Doppelten der in der Literatur als Radius der Mohrschen Kreise definierten deviatorischen Spannung.

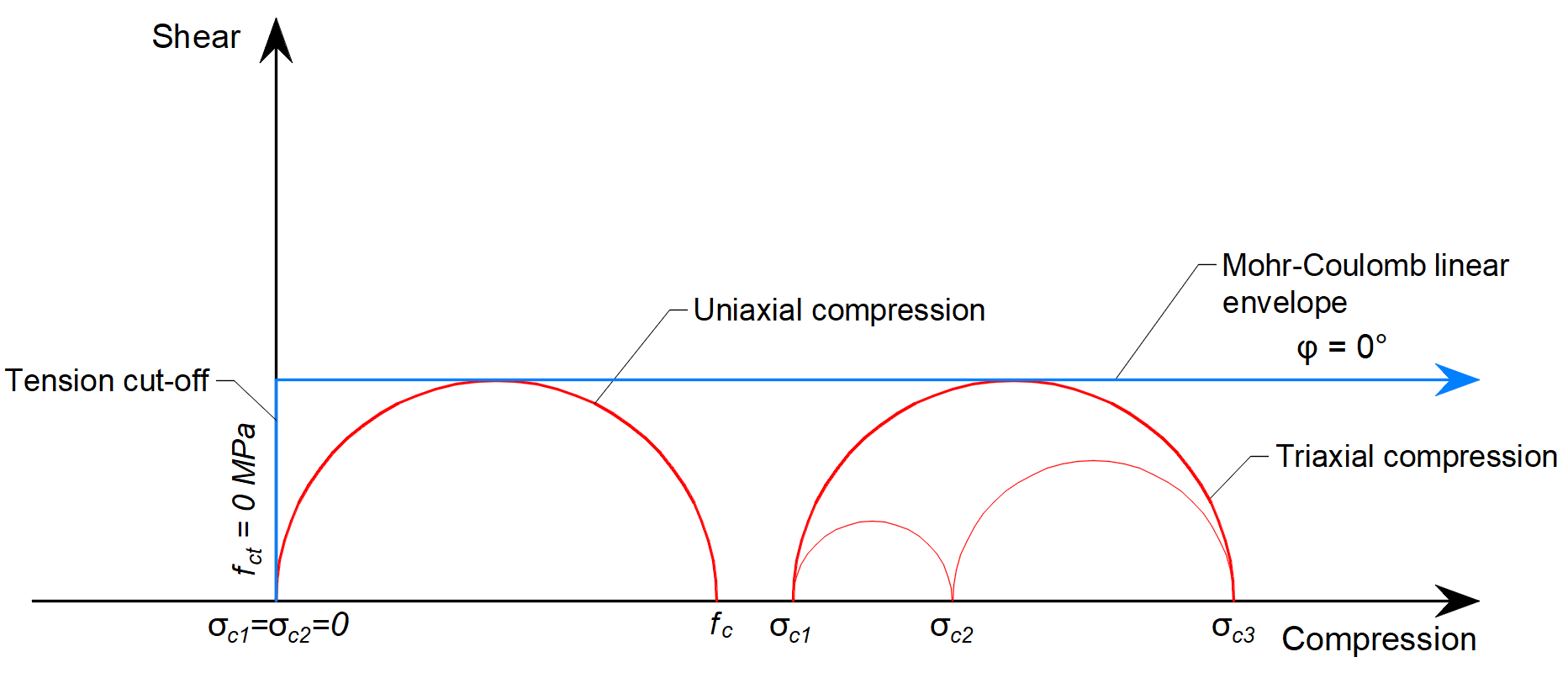
In der in IDEA StatiCa Detail implementierten 3D-CSFM wird der Winkel der inneren Reibung mit φ = 0° angenommen , wie in Abbildung 6 dargestellt.

\[ \textsf{\textit{\footnotesize{Abb. 6\qquad Mohrsche Kreise für Beton, implementiert in IDEA StatiCa Detail}}}\]

Die praktische Folge dieser Implementierung ist, dass die maximale Differenz zwischen σ_c3 und σ_c1 konstant ist, wenn σ_c3 zunimmt.

Die äquivalente Hauptspannung drückt die äquivalente einachsige Spannung für einen allgemeinen triaxialen Spannungszustand aus.

\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]

Der σ_c_,eq-Wert kann daher direkt mit den Grenzwerten für die einachsige Festigkeit gemäß den Normen verglichen werden.

\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} \le 1\]

Dabei ist σ_c_,lim die bemessene (faktorisierte) einachsige Festigkeit des Betons f_c.

Vergleicht man Abbildung 5, in der der reale innere Reibungswinkel verwendet wird, mit Abbildung 6, die die Umsetzung der Mohr-Coulomb-Theorie mit einem inneren Reibungswinkel von Null zeigt, so wird deutlich, dass der für die Berechnungen im Detail gewählte Ansatz sehr konservativ für die Berücksichtigung des dreiachsigen Spannungszustands ist.

Zum besseren Verständnis der von triaxialer Druckbeanspruchung betroffenen Bereiche wurde der IDEA StatiCa Detail-Anwendung der Ausdruck für den Anstieg der effektiven Materialfestigkeit infolge triaxialer Druckbeanspruchung als Verhältnis σ_c3/σ_c_,lim hinzugefügt. Sie finden dieses Verhältnis in der Festigkeitskontrolle.

In den Hilfsergebnissen kann der Benutzer auch den κ-Faktor finden, der die Triaxialität auf andere Weise erklärt.

\[\kappa = \frac{ \sigma_{c3}}{ \sigma_{c,eq}}\]

Der Betonfestigkeitsnachweis kann dann umgeschrieben werden als:

\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} = \frac{\sigma_{c,3} }{ \kappa \cdot \sigma_{c,lim}} \le 1\]

Daraus folgt, dass, wenn das Element unter hydrostatischer Spannung steht - σ_c3=σ_c2=σ_c1, die äquivalente Hauptspannung σ_c_,eq den Wert Null hat und der Kappa-Faktor unendlich wird.

Mehr dazu finden Sie hier: Triaxiale Spannung - der aktive Begrenzungseffekt

Allgemeine Mechanik-Annahmen für 3D CSFM

Gleichgewichtsgleichungen

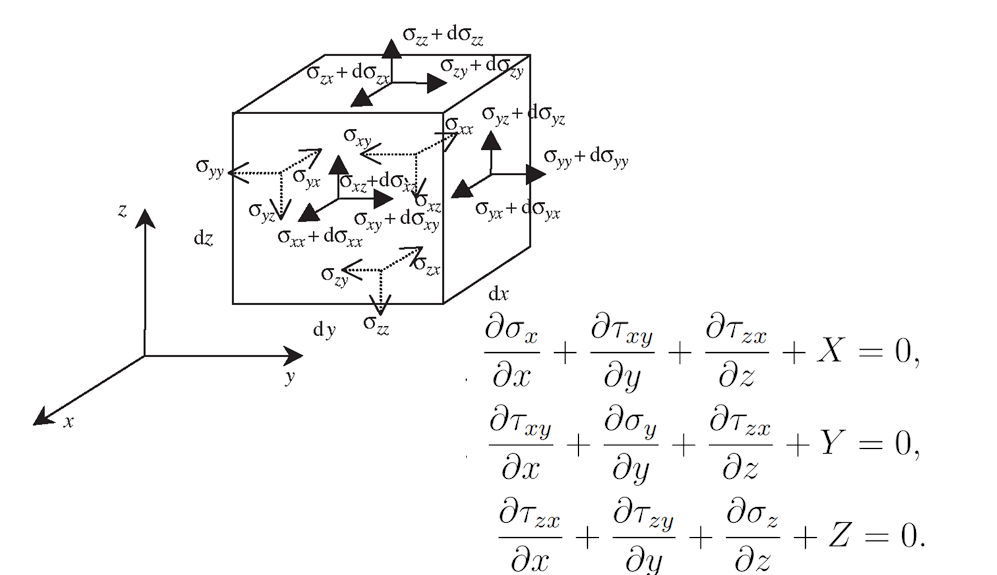
Die Theorie der kleinen Verformungen ermöglicht die Aufstellung der Gleichgewichtsgleichung auf der Grundlage des unverformten Volumens unter Verwendung eines Ansatzes erster Ordnung.

\[ \textsf{\textit{\footnotesize{Abb. 7\qquad Gleichgewichtsgleichungen und grafische Darstellung auf einem infinitesimalen Element}}}\]

Kompatibilitätsgleichungen

Ein Festkörper besteht aus infinitesimalen Volumina oder Materialpunkten, die jeweils lückenlos und überlappungsfrei miteinander verbunden sind. Damit bei der Verformung eines Kontinuumskörpers keine Lücken oder Überlappungen entstehen, müssen mathematische Bedingungen eingehalten werden.

Konstitutive Gleichungen

Die konstitutiven Gleichungen, die das Verhalten von 3D-Elementen bestimmen, spielen eine zentrale Rolle bei der Analyse des Materialverhaltens in der Strukturmechanik. Diese Gleichungen sind so formuliert, dass sie das nichtlineare isotrope Verhalten berücksichtigen, das für massive Blockstäbe in IDEA StatiCa Detail gilt.

Bei einer 3D-Wand ist es wichtig, das orthotrope Verhalten über die gesamte Dicke zu berücksichtigen, wobei die Spannungen im Beton aufgrund der fehlenden Querbewehrung besonders zu beachten sind. Die Orthotropie wird dadurch verursacht, dass die Spannung im Beton in einer Richtung außerhalb der Ebene zugelassen wird. Die Materialeigenschaften wie die Modulelastizität und die Poissonzahl bleiben gleich.

\[ \textsf{\textit{\footnotesize{Abb. 8\qquad Lineare elastische isotrope Nachgiebigkeitsmatrix}}}\]

Analysemodell von IDEA StatiCa 3D Detail

Einführung in die Finite-Elemente-Implementierung

3D CSFM berücksichtigt kontinuierliche Spannungsfelder im Beton (3D finite Elemente), die durch diskrete "Stab"-Elemente ergänzt werden, die die Bewehrung darstellen (1D finite Elemente). Daher ist die Bewehrung nicht diffus in die 3D-Finite-Elemente eingebettet, sondern explizit modelliert und mit ihnen verbunden.

\Abb. 9: Quadratur des Berechnungsmodells für Betonblock und außerebene Wand}}}]

Finite-Elemente-Typen

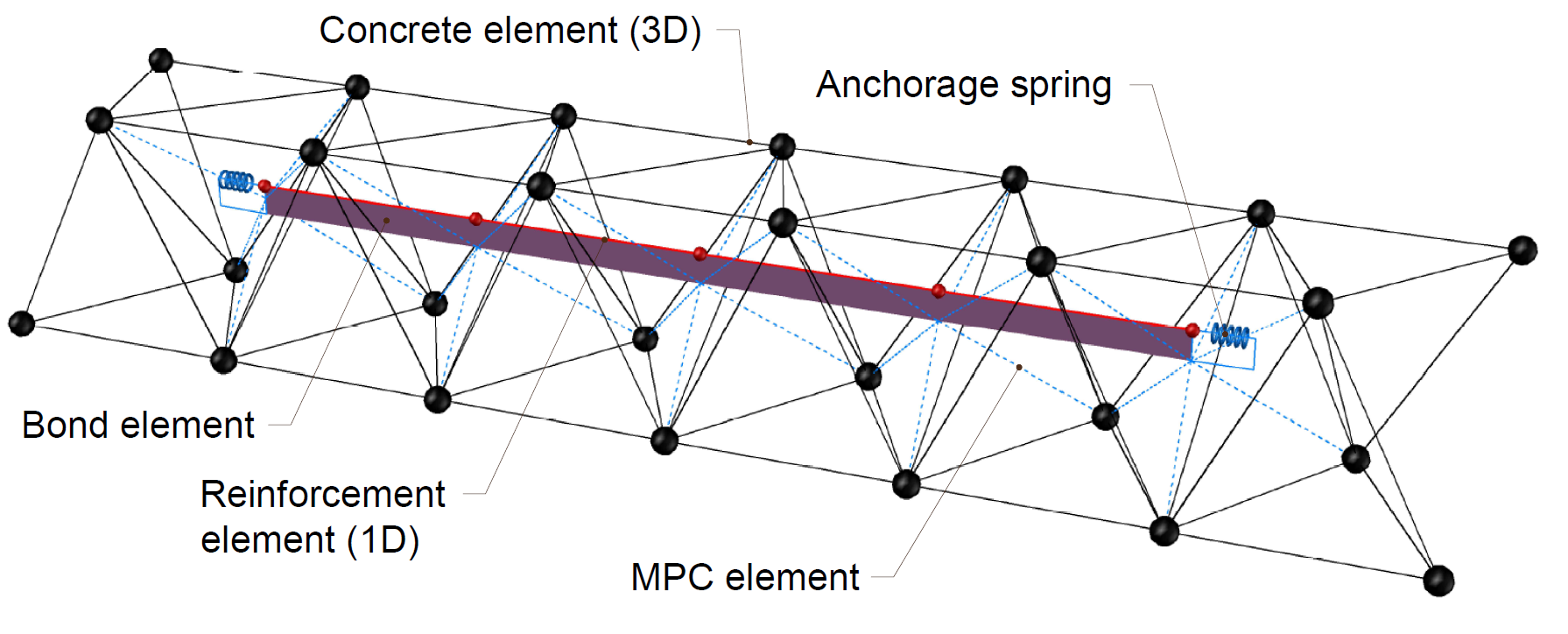
Das nichtlineare Finite-Elemente-Analysemodell besteht aus mehreren Arten von Finite-Elementen, die zur Modellierung des Betons, der Bewehrung und der Verbindung zwischen diesen Elementen verwendet werden. Die Beton- und Bewehrungselemente werden zunächst unabhängig voneinander vernetzt und dann mit Hilfe von Multi-Point-Constraints (MPC-Elementen) miteinander verbunden. Dadurch kann die Bewehrung jede beliebige Position einnehmen, die nicht auf die Knoten des tetraedrischen Netzes beschränkt ist. Um die Verankerungslänge, den Verbund und das Verankerungsende zu überprüfen, werden Federelemente zwischen der Bewehrung und den MPC-Elementen eingefügt.

\[ \textsf{\textit{\footnotesize{Abb. 10\qquad Finite-Elemente-Modell: Bewehrungselemente auf Betonnetz mit MPC- und Verbundelementen abgebildet}}}\]

Beton

Beton wird mit gemischten tetraedrischen Elementen modelliert, die Knotenrotationen berücksichtigen. Die tetraedrischen Elemente erlauben eine Vernetzung von Regionen mit beliebiger Topologie. Die implementierte Formulierung garantiert präzise Verformungsergebnisse – ohne unerwünschte Schubspannungen, die als Shear Locking-Effekt bekannt sind – selbst bei groben Netzen.

Es wird die vollständige Integration verwendet. Das bedeutet, dass jedes Element mit vier Integrationspunkten ausgestattet ist, die sich innerhalb des Volumens befinden. Eine solche Integration liefert ein präzises Dehnungs- und Spannungsfeld, das eine ausreichende Auswertung und Darstellung der Ergebnisse über das gesamte Volumen ermöglicht.

Bewehrung

Bewehrungsstäbe werden durch 1D-Stab"-Elemente (CROD) mit zwei Knoten modelliert, die nur eine axiale Steifigkeit aufweisen. Diese Elemente sind mit speziellen "Bond"-Elementen verbunden, die entwickelt wurden, um das Verbundverhalten zwischen einem Bewehrungsstab und dem umgebenden Beton zu modellieren. Diese Verbundelemente werden anschließend über MPC-Elemente (Multi-Point-Constraint) mit dem Netz verbunden, das den Beton darstellt. Dieser Ansatz ermöglicht die unabhängige Vernetzung von Bewehrung und Beton, während ihre Verbindung untereinander später sichergestellt wird.

Verbundelemente

Die Verankerungslänge wird durch die Implementierung der Verbundschubspannungen zwischen Betonelementen (3D) und Bewehrungselementen (1D) im Finite-Elemente-Modell nachgewiesen. Zu diesem Zweck wurde der Finite-Elemente-Typ "Verbund" entwickelt.

Das Verbundelement ist definiert als ein finites Schalenelement, das mit Elementen, die die Bewehrung darstellen, über die erste Schicht und über die zweite Schicht mit dem Betonnetz über Mehrpunkt-Zwangsbedingungen (MPC-Elemente) verbunden ist.

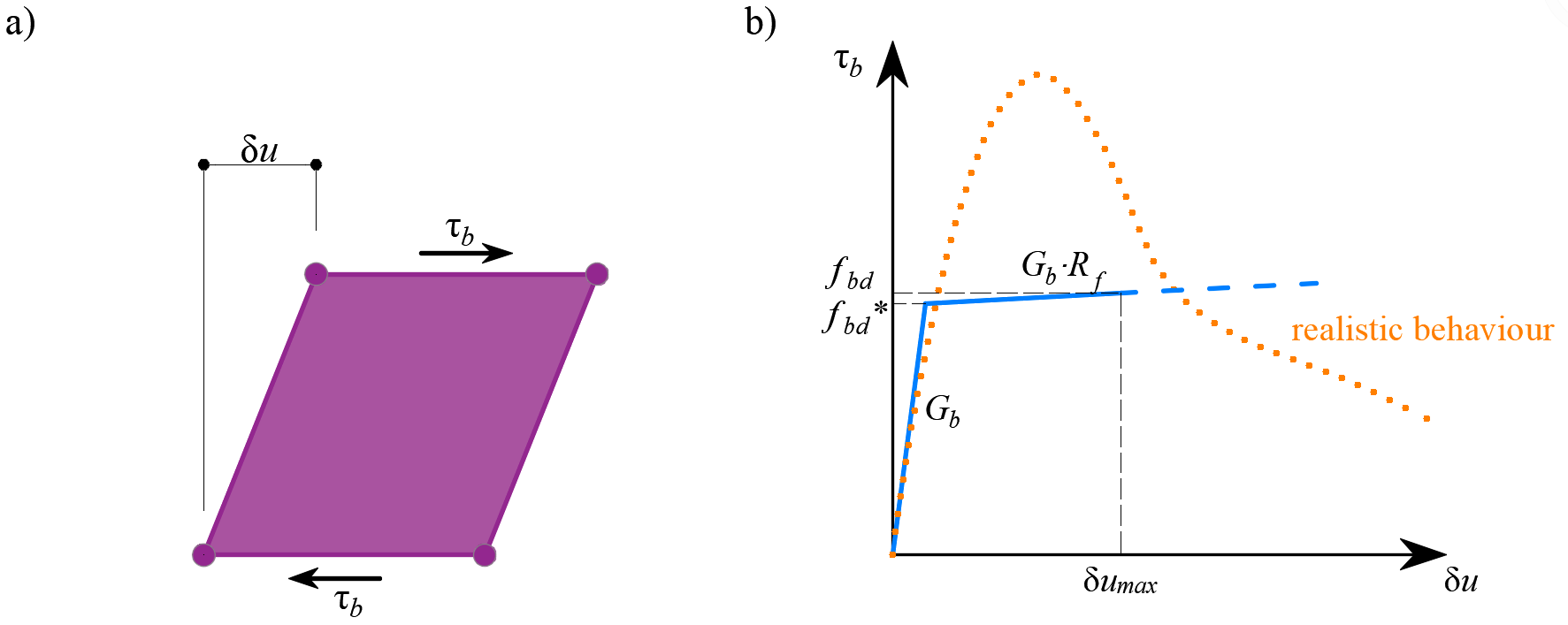
Das Verhalten dieses Elements wird durch die Verbundspannung τ_b als bilineare Funktion des Schlupfs zwischen dem oberen und dem unteren Knoten δu beschrieben, siehe (Abb. 11).

\[ \textsf{\textit{\footnotesize{Abb. 11\qquad (a) Konzeptuelle Darstellung der Verformung eines Verbundelements; (b) Scher-Verformungsfunktion}}}\]

Der elastische Steifigkeitsmodul der Bond-Slip-Beziehung, Gb, ist wie folgt definiert:

\[G_b = k_g \cdot \frac{E_c}{Ø}\]

k_g Koeffizient in Abhängigkeit von der Oberfläche des Bewehrungsstabs (standardmäßig k_g = 0,2)

E_c Elastizitätsmodul des Betons (im Falle von EN als E_cm angenommen)

Ø der Durchmesser des Bewehrungsstabs

Für den Nachweis der Verankerungslänge werden die Bemessungswerte (faktorisierte Werte) der Verbundschubspannung f_bd verwendet, die in den jeweils gewählten Bemessungsregeln DIN EN 1992-1-1 angegeben sind. Die Verfestigung des plastischen Astes wird standardmäßig mit Gb/105 berechnet.

Verankerungsfeder

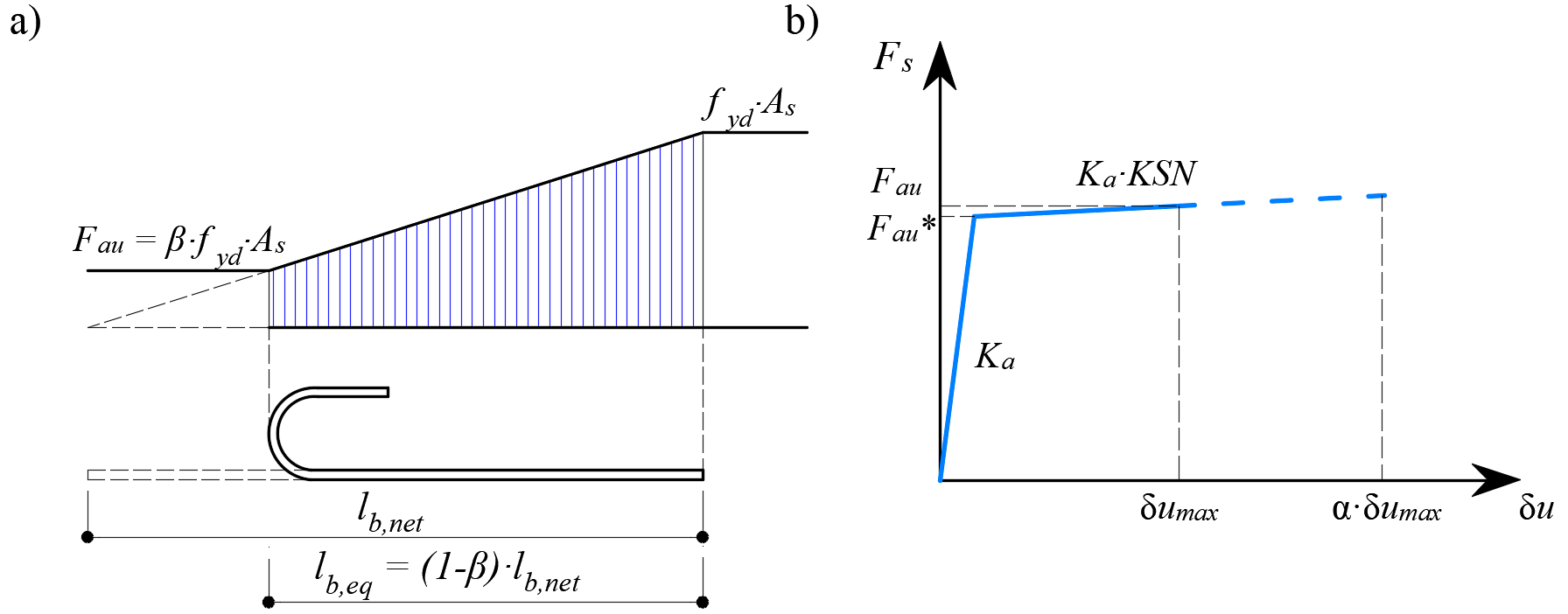
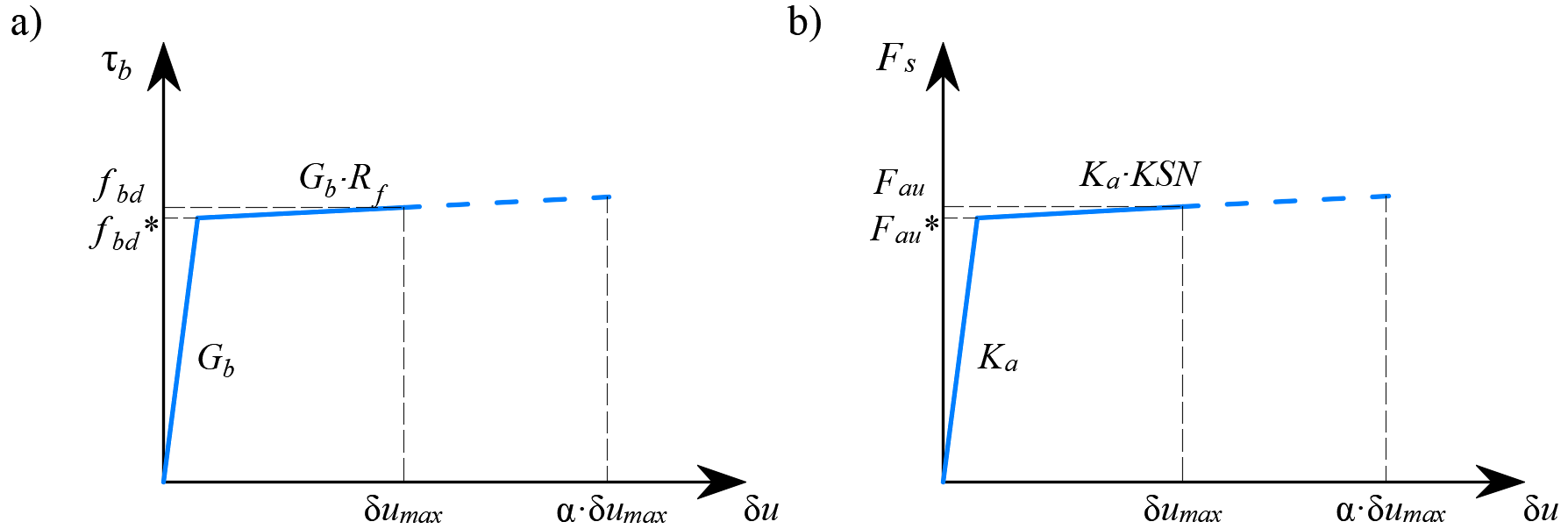
Das Anbringen von Verankerungsenden an den Bewehrungsstäben (d.h. Haken, Schlaufen...), die den Vorschriften der Bemessungsnormen entsprechen, ermöglicht die Verringerung der Grundverankerungslänge der Stäbe(l_b,net) um einen bestimmten Faktor β (im Folgenden als "Verankerungsbeiwert" bezeichnet). Der Bemessungswert der Verankerungslänge(l_b) wird dann wie folgt berechnet:

\[ \textsf{\textit{\footnotesize{Abb. 12\qquad Modell für die Reduzierung der Verankerungslänge: a) Verankerungskraft entlang der Verankerungslänge von}}}\] \[ \textsf{\textit{\footnotesize{Bewehrungsstab, b) Schlupf-Verankerungskraft-Wirkungsgesetz}}}\]

Die Reduzierung der Verankerungslänge wird im Finite-Elemente-Modell durch ein Federelement am Stabende (Abb. 12a) berücksichtigt, das durch das in (Abb. 12b) dargestellte konstitutive Modell definiert ist. Die maximale Kraft, die von dieser Feder übertragen wird(F_au), beträgt:

\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]

wobei :

β der Verankerungskoeffizient auf der Grundlage der Verankerungsart

A_s der Querschnitt des Bewehrungsstabs

f_yd der Bemessungswert (faktorisierter Wert) der Streckgrenze der Bewehrung

Lastübertragung

Fußplatte

Die Fußplatte wird als lineares Schalenelement modelliert. Das für die Bodenplatte verwendete Stahlmaterial wird in der Registerkarte Materialien definiert.

\[ \textsf{\textit{\footnotesize{Abb. 13\qquad Die Materialdefinition der Grundplatte}}}\]

Die Fußplatte kann durch Punktlasten (Fx, Fy, Fz, Mx, My, Mz) und Kraftgruppen (Fx, Fy, Fz) belastet werden, die hauptsächlich für Belastungsmodelle verwendet werden, die aus der IDEA StatiCa Connection exportiert werden. Beachten Sie, dass Punktlasten und Punktmomente direkt den entsprechenden Knoten der Grundplatte belasten. Das bedeutet, dass es keine Umverteilung gibt, nur durch die Steifigkeit der Grundplatte.

Diese Implementierung erlaubt es, Lasteinwirkungen aus der IDEA StatiCa Connection zu importieren, die auf die Fußplatte an der Stelle der einzelnen finiten Elemente der Schweißnaht aufgebracht werden, wobei der Wert und die Richtung aus der allgemeinen Spannung dieses finiten Elements der Schweißnaht bestimmt werden. Mehr dazu kann im entsprechenden Kapitel dieses Dokuments nachgelesen werden.

Zwischen der Grundplatte und dem Beton wird ein reiner Reibungskontakt definiert. Für die Querkraftübertragung kann der Anwender zwischen drei Optionen wählen:

Durch Dübel bzw. Anker
Durch Reibung
Durch Schubknagge

Die Software lässt die Kombination dieser Schubübertragungsmechanismen nicht zu.

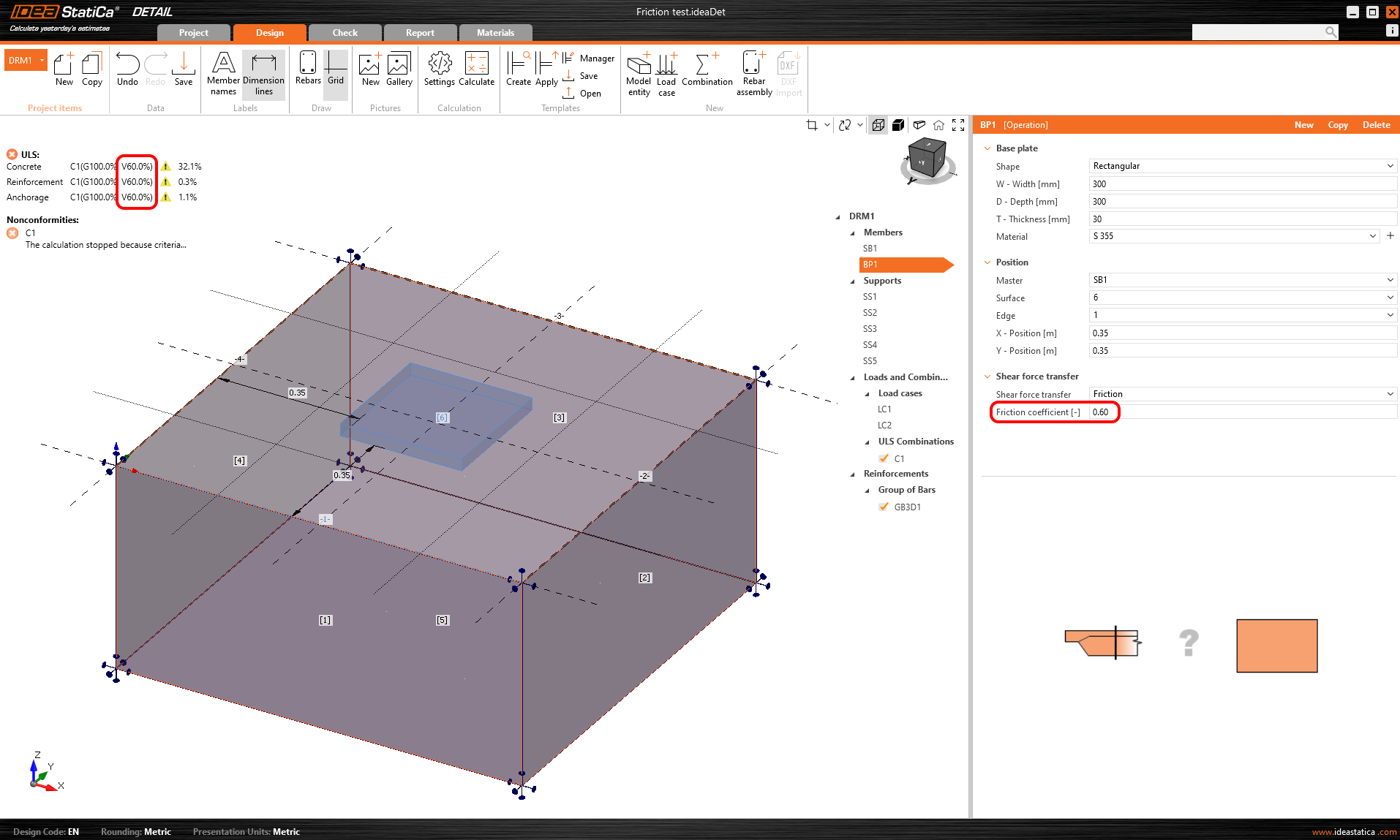
Der Reibungskoeffizient ist als dimensionloser Wert einzugeben. Wenn die resultierende Querkraft F_xy die Druckkraft F_z mal den Reibungskoeffizienten μ übersteigt, bricht die Berechnung ab und nicht alle Lasten werden auf das Modell angewendet. Die Bedingung wird wie folgt formuliert:

\[\frac {F_{xy}}{ \mu \cdot F_{z}}\le 1\]

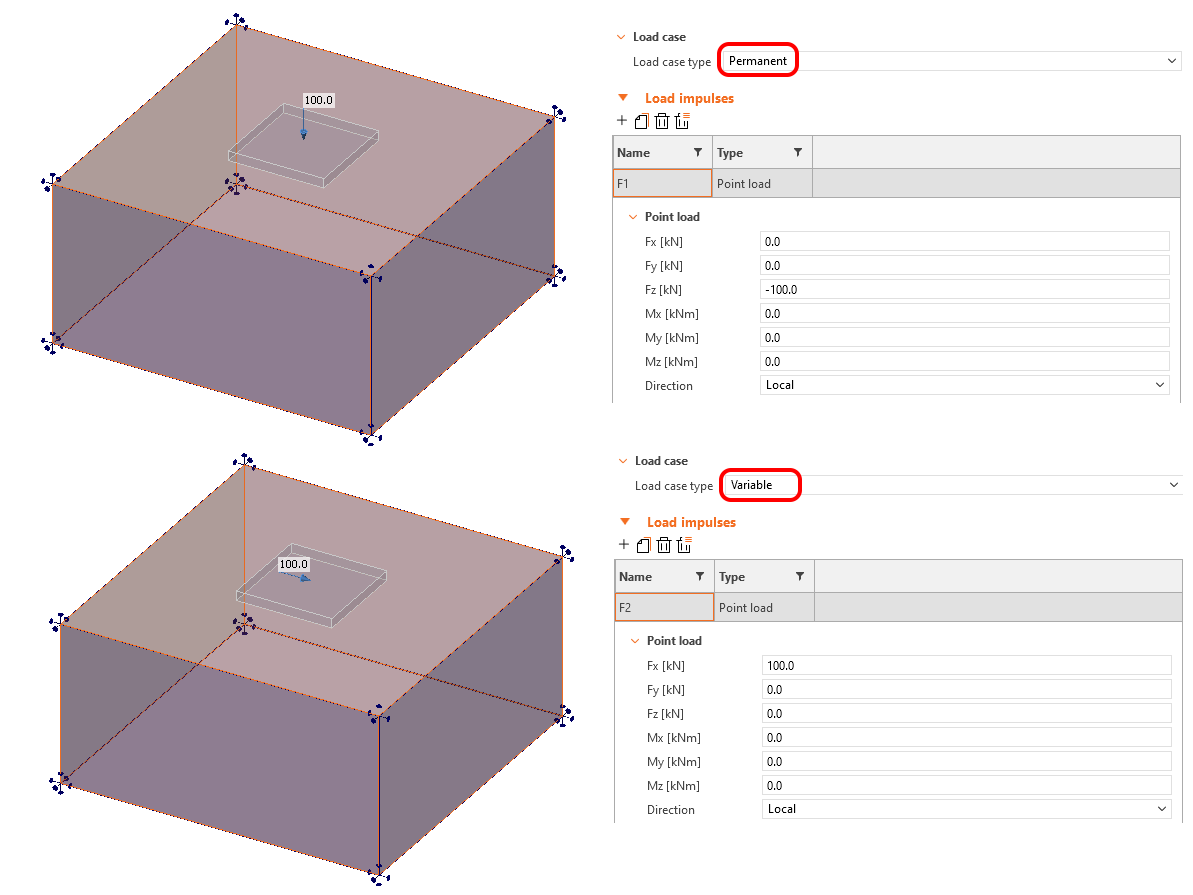
Dies wird in dem folgenden Beispiel deutlich, in dem zwei Lastfälle betrachtet werden.

LC1 - Ständiger Typ - F_z = 100 kN
LC2 - veränderlicher Typ - F_x = 100 kN

\[ \textsf{\textit{\footnotesize{Abb. 14\qquad Lasteinleitung für das Beispiel zur Erläuterung der Scherübertragung durch Reibung}}}\]

Im ersten Berechnungsschritt wird die gesamte ständige Last aufgebracht. Dann wird die variable Last schrittweise aufgebracht, bis sie den Wert der Drucklast mal Reibungskoeffizient erreicht.

\[ \textsf{\textit{\footnotesize{Abb. 15\qquad Ergebnisse aus dem Beispiel zur Erläuterung der Scherübertragung durch Reibung}}}\]

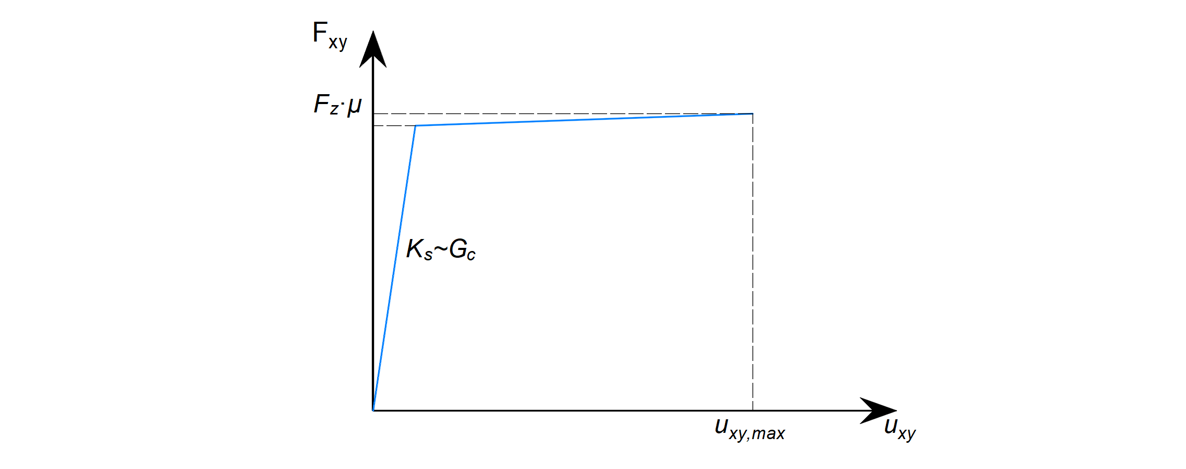
Das Diagramm in Abbildung 16 beschreibt das Verhalten des Reibungskontakts zwischen der Fußplatte und dem Beton.

\[ \textsf{\textit{\footnotesize{Abb. 16\qquad Kraft-Weg-Diagramm, das das Verhalten des Reibungskontakts beschreibt}}}\]

Der Wert von F_zμ ist für jeden Schritt der Berechnung unterschiedlich, während der Wert der maximalen Scherverformung u_xy konstant ist.

Wenn die Drucknormalkraft F_z und die Querkraft F_xy in einer Lastfallart (z. B. nur permanent) eingegeben werden und die Bedingung F_xy / (F_zμ) ≤ 1 nicht erfüllt ist, wird keine Last auf das Modell aufgebracht, da die Bedingung in keinem Inkrement der Berechnung erfüllt ist.

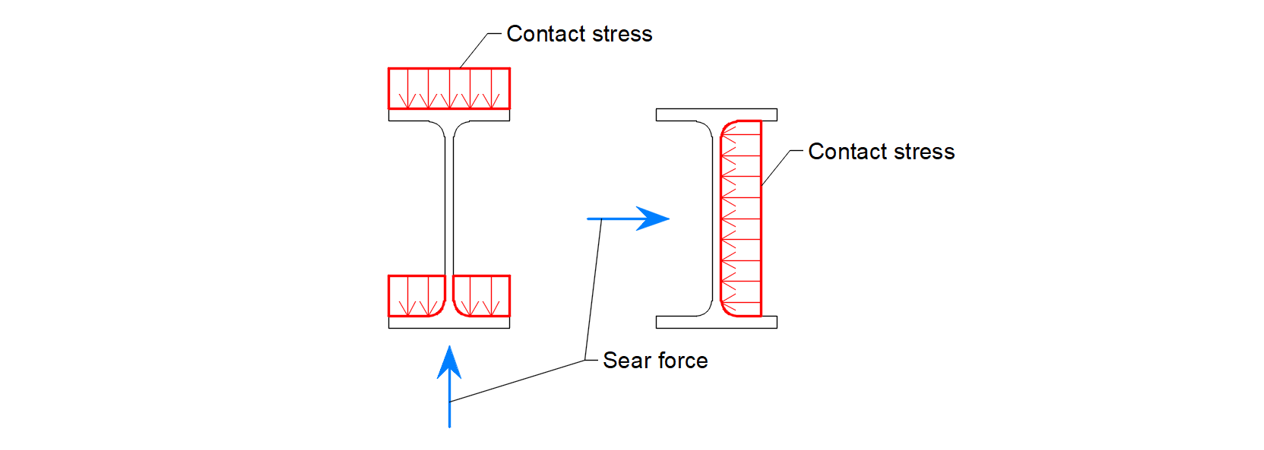
Die Schubknagge ist mit dem Betonnetz durch Zwangsbedingungen verbunden, die nur Druck- und Normalspannungsübertragung zulassen.

\[ \textsf{\textit{\footnotesize{Abb. 17\qquad Scherfahnenübertragung des Schubmechanismus}}}\]

Die Schubknagge wird aus linearen Schalenelementen modelliert, wobei der Elastizitätsmodul E das Material definiert.

Die Ergebnisse werden sowohl für die Fußplatte als auch für die Schubknagge nicht ausgewertet und dargestellt.

Verankerungen

Die finiten Elemente, die die Anker darstellen, werden so modelliert, dass sie in der Lage sind, Normal- und Querkräfte auf den Beton zu übertragen, wobei auch die Biegesteifigkeit der Anker berücksichtigt wird. Zur Modellierung des Schlupfes zwischen dem Anker und dem umgebenden Beton werden die gleichen Verbund- und MPC-Elemente wie für die Bewehrung verwendet. Mit dem Unterschied, dass es bei Klebeankern möglich ist, die Bemessungsverbundfestigkeit anzugeben.

Dübel können mit Fußplatten verbunden werden. Für diese Verbindung wird eine vollständig nichtlineare Zwangsbedingung verwendet, um das Ende des Ankers und einen Knoten der Grundplatte zu verbinden. Mit diesem Element können alle Freiheitsgrade kontrolliert werden, um z.B. sicherzustellen, dass kein Druck von den Dübeln auf die Grundplatte ohne Abstand übertragen wird, oder dass kein Schub vom Dübel übertragen wird, wenn eine Schubknagge modelliert wird, usw.

Die Einstellungen für die Verbindung mit der Fußplatte für Anker erlauben es dem Benutzer zu kontrollieren, ob und wie der Anker mit der Fußplatte durch die zuvor erwähnte Einschränkung verbunden wird.

In der aktuellen Version wird nur der direkte Kontakt zwischen der Grundplatte und dem Beton unterstützt.

Die Druckkraft wird bei direktem Kontakt nicht von der Fußplatte auf den Anker übertragen. Die Druckkraft wird nur durch den Kontakt zwischen der Fußplatte und dem Beton übertragen.

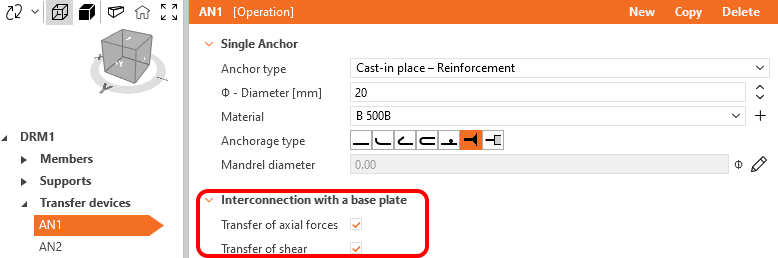
Mit dem Kontrollkästchen Übertragung von Axialkräften kann gesteuert werden, ob Anker und Fußplatte auf Zug verbunden werden oder nicht. Dies wird vor allem für den Export aus der Funktion Anschluss verwendet (siehe entsprechendes Kapitel). Für die manuelle Modellierung ist es sinnvoll, dieses Kontrollkästchen immer aktiviert zu lassen.

Mit dem Kontrollkästchen Schubkraftübertragung kann gesteuert werden, ob Anker und Grundplatte schubtechnisch miteinander verbunden werden sollen oder nicht. Beachten Sie, dass es nicht unterstützt wird, Schubübertragungsmechanismen zu kombinieren, so dass dieses Kontrollkästchen für die Übertragung durch Reibung und Scherfahne irrelevant ist. Andererseits bietet dieses Feld bei der Schubumlagerung mit Ankern die Möglichkeit, einige Anker von der Schubumlagerung auszuschließen.

FE-Netzgenerierung in 3D CSFM

Die finiten Elemente werden intern implementiert, und das Analysemodell wird automatisch erstellt, ohne dass der Benutzer spezielles Fachwissen dafür benötigt. Ein zentraler Bestandteil dieses Prozesses ist die Netzgenerierung.

Beton

Alle Betonteile werden gemeinsam vernetzt. Eine empfohlene Elementgröße wird von der Anwendung automatisch auf der Grundlage der Größe und Form der Struktur und unter Berücksichtigung des Durchmessers des größten Bewehrungsstabs berechnet. Außerdem garantiert die empfohlene Elementgröße, dass in dünnen Teilen der Struktur, wie z. B. schlanken Stützen oder dünnen Wänden, mindestens vier Elemente erzeugt werden, um in diesen Bereichen zuverlässige Ergebnisse zu gewährleisten. Die Tragwerksplaner können jederzeit eine benutzerdefinierte Betonelementgröße auswählen, indem sie den Multiplikator der Standardmaschengröße ändern.

Bewehrung

Die Bewehrung wird in Elemente unterteilt, die in etwa die gleiche Länge wie die Betonelementgröße haben. Sobald die Bewehrungs- und Betonnetze erzeugt sind, werden sie mit Verbundelementen verbunden, wie in Abb. 9 gezeigt.

Verfeinerung

Die Betonelemente werden automatisch, um die Anker und um die Schubknagge verfeinert. Die Größe des verfeinerten Netzes ist standardmäßig doppelt so groß wie die des Basisbetonnetzes. Der Radius des verfeinerten Bereichs ist definiert als die Elementgröße multipliziert mit zwei.

Die Lösungsmethode und der Lastkontrollalgorithmus für 3D CSFM

Für die Lösung eines nichtlinearen FEM-Problems wird der Standard-Newton-Raphson-Algorithmus (NR) verwendet.

Im Allgemeinen konvergiert der NR-Algorithmus oft nicht, wenn die volle Last in einem einzigen Schritt aufgebracht wird. Ein üblicher Ansatz, der auch hier verwendet wird, besteht darin, die Last sequentiell in mehreren Inkrementen aufzubringen und das Ergebnis des vorherigen Lastinkrements zu verwenden, um die Newton-Lösung des nachfolgenden Inkrements zu starten. Zu diesem Zweck wurde ein Lastkontrollalgorithmus zusätzlich zum Newton-Raphson implementiert. Für den Fall, dass die NR-Iterationen nicht konvergieren, wird das aktuelle Lastinkrement auf die Hälfte seines Wertes reduziert und die NR-Iterationen werden erneut versucht.

Ein zweiter Zweck des Lastkontrollalgorithmus besteht darin, die kritische Last zu finden, die bestimmten "Stoppkriterien" entspricht - insbesondere der maximalen Dehnung im Beton, dem maximalen Schlupf in den Verbundelementen, der maximalen Verschiebung in den Verankerungselementen und der maximalen Dehnung in den Bewehrungsstäben. Die kritische Last wird mit Hilfe der Halbierungsmethode ermittelt. Wird das Stoppkriterium irgendwo im Modell überschritten, werden die Ergebnisse des letzten Lastinkrements verworfen und ein neues Inkrement von der Hälfte der Größe des vorherigen berechnet. Dieser Vorgang wird so lange wiederholt, bis die kritische Last mit einer bestimmten Fehlertoleranz gefunden ist.

Für Beton wurde das Stoppkriterium auf eine Druckdehnung von 5% (d.h. etwa eine Größenordnung größer als die tatsächliche Versagensdehnung von Beton) und eine Zugdehnung von 7% an den Integrationspunkten der Schalenelemente festgelegt. Im Zugbereich wurde der Wert so gewählt, dass die Grenzdehnung in der Bewehrung, die ohne Berücksichtigung der Zugversteifung in der Regel bei 5 % liegt, zuerst erreicht wird. Im Druckbereich wurde der Wert aus mehreren Alternativen so gewählt, dass er groß genug ist, um die Auswirkungen von Stauchungen in den Ergebnissen sichtbar zu machen, aber klein genug, um nicht zu viele Probleme mit der numerischen Stabilität zu verursachen.

\[ \textsf{\textit{\footnotesize{Abb. 13\qquad Konstitutives Gesetz der Verbund- und Verankerungselemente, die für den Nachweis der Verankerungslänge }}}\] \[ \textsf{\textit{\footnotesize{verwendet werden: a) Verbundschubspannung Rutschverhalten eines Verbundelements,}}}\] \[ \textsf{\textit{\footnotesize{b) Kraft-Weg-Verhalten eines Verankerungselements}}}\]

Für die Bewehrung wird das Haltekriterium in Form von Spannungen definiert. Da die Spannungen am Riss modelliert werden, entspricht das Kriterium auf Zug der Zugfestigkeit der Bewehrung unter Berücksichtigung des Sicherheitsbeiwerts. Derselbe Wert wird für das Kriterium in Druckrichtung verwendet.

Das Anhaltekriterium in Verbundelementen und Verankerungsfedern ist α·δ_umax, wobei δ_umax der maximale Schlupf ist, der in den Nachweisen verwendet wird, und α = 10.

Darstellung der 3D-Ergebnisse

Die Ergebnisse werden unabhängig voneinander für Beton und für Bewehrungselemente dargestellt. Die Spannungs- und Dehnungswerte im Beton werden an den Integrationspunkten der Volumenelemente berechnet. Da es jedoch nicht praktikabel ist, die Daten auf diese Weise darzustellen, werden die Ergebnisse standardmäßig in Knoten dargestellt, wie der Höchstwert der Druckspannung von benachbarten Gauß-Integrationspunkten in verbundenen Elementen.

Die Ergebnisse für die finiten Elemente der Bewehrung sind entweder konstant für jedes Element (ein Wert - z. B. für Stahlspannungen) oder linear (zwei Werte - für Verbundergebnisse). Für Hilfselemente, wie z. B. Elemente von Tragplatten, werden nur die Verformungen dargestellt.

Modell importiert von IDEA StatiCa Connection

Das IDEA Detail 3D Modell muss nicht immer von Grund auf oder aus einer Vorlage modelliert werden. Es besteht auch die Möglichkeit, das Modell inklusive Lasteinwirkungen aus IDEA StatiCa Connection zu importieren. Die Geometrie des Betonblocks, der Anker, der Bodenplatte, der Materialien und der Lasteinwirkungen werden automatisch übernommen.

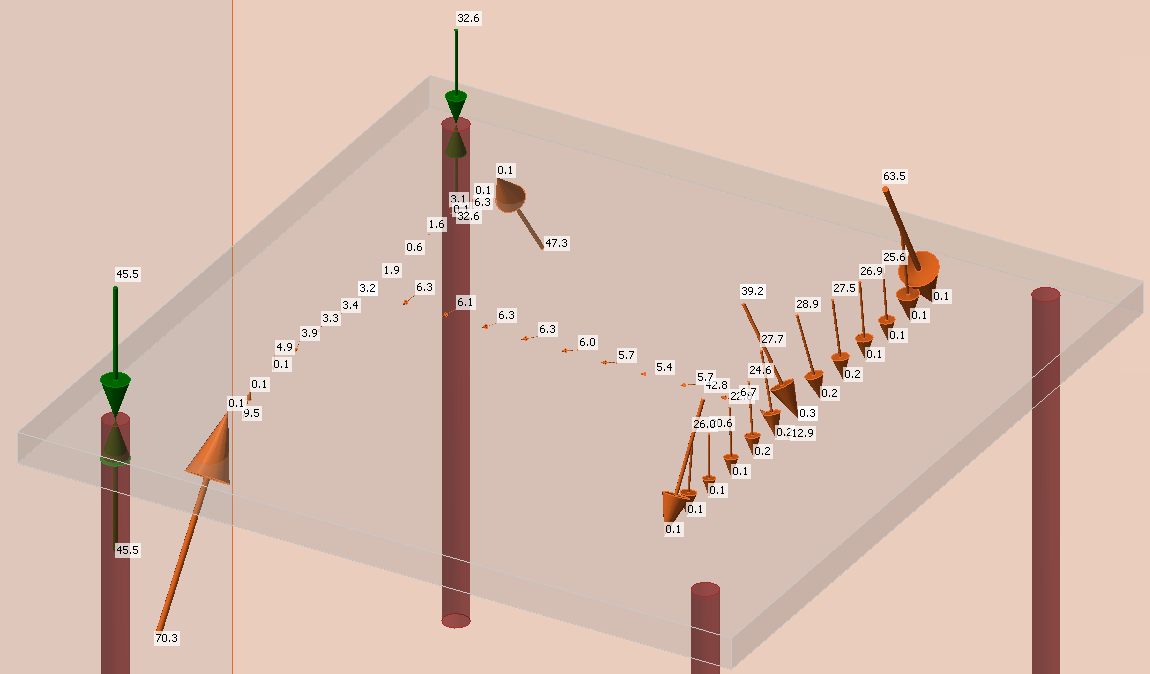
\[ \textsf{\textit{\footnotesize{Abb. 16\qquad Aus IDEA StatiCa Connection importierte Lasten}}}\]

Die Fußplatte wird durch eine Gruppe von Kräften belastet, die aus der allgemeinen Spannung jedes finiten Elements der Schweißnähte, die das Stahlteil und die Fußplatte verbinden, bestimmt werden.

Da die Definition der einzelnen Komponenten in Connection und Detail unterschiedlich ist (z.B. wird die Fußplatte in Detail durch ein lineares Material modelliert, während sie in Connection durch ein plastisches Material modelliert wird), würde es eine unterschiedliche Umverteilung der Lasten zwischen dem Fußplatten-Beton-Kontakt und den Ankern bzw. zwischen den Ankern selbst geben. Mit anderen Worten, es gäbe unterschiedliche Zugnormalkräfte in den Ankern in Connection und Detail. Aus diesem Grund werden die Anker für die Normalkräfte (in Richtung des Dübels) von der Fußplatte abgekoppelt und die Anker direkt mit den angreifenden Zugkräften belastet. Außerdem müssen die entgegengesetzten Kräfte, die die Fußplatte an der Ankerstelle belasten, addiert werden, um das Modell ins Gleichgewicht zu bringen. Diese beiden entgegengesetzten Kräfte sind in Abbildung 16 dargestellt.

Die Querkräfte werden jedoch durch die Verbindung von Fußplatte und Anker (oder Schubknagge oder Reibung) übertragen. Dieses Verhalten ist möglich, weil es eine Zwangsbedingung gibt, die die Grundplatte und den Anker verbindet und es uns ermöglicht, alle Freiheitsgrade dieser Verbindung zu kontrollieren.

Überprüfung des Modells

Grenzzustände

Grenzzustand der Tragfähigkeit

Die verschiedenen Nachweise, die von bestimmten Bemessungsnormen gefordert werden, werden auf der Grundlage der vom Modell gelieferten direkten Ergebnisse bewertet. Die GZT-Nachweise werden für die Betonfestigkeit, die Bewehrungsfestigkeit und die Verankerung (Verbundschubspannungen) geführt.

Um eine effiziente Bemessung eines Bauteils zu gewährleisten, ist es empfehlenswert, eine Voranalyse durchzuführen, die die folgenden Schritte berücksichtigt:

Wählen Sie eine Auswahl der kritischsten Lastfallkombinationen.
Berechnen Sie nur Lastkombinationen im Grenzzustand der Tragfähigkeit (GZT).
Um die Berechnungszeit zu verkürzen und eventuelle Probleme zu lösen, sollten Sie ein grobes Netz verwenden, indem Sie den Multiplikator der Standardnetzgröße im Setup erhöhen (Abb. 14). Wenn das Modell gut funktioniert, setzen Sie den Multiplikator wieder auf den Faktor 1 zurück.

\[ \textsf{\textit{\footnotesize{Abb.14\qquad Mesh-Multiplikator}}}\]

Die grundlegenden Ergebnisse und Nachweise (Spannung, Dehnung und Ausnutzung (d.h. der berechnete Wert/Grenzwert aus dem Code)) sowie die Richtung der Hauptspannungen im Falle von Betonelementen) werden mit Hilfe verschiedener Diagramme dargestellt, wobei Druck im Allgemeinen in rot und Zug in blau dargestellt wird. Globale Minimal- und Maximalwerte für die gesamte Struktur können ebenso hervorgehoben werden wie Minimal- und Maximalwerte für jedes benutzerdefinierte Teil. In einer separaten Registerkarte des Programms können erweiterte Ergebnisse wie Tensorwerte, Verformungen der Struktur und Bewehrungsgrade (effektiv und geometrisch), angezeigt werden. Außerdem können Lasten und Reaktionen für ausgewählte Kombinationen oder Lastfälle dargestellt werden.

Strukturelementnachweise nach Eurocode

Werkstoffmodelle in 3D CSFM (EN)

Beton - GZT

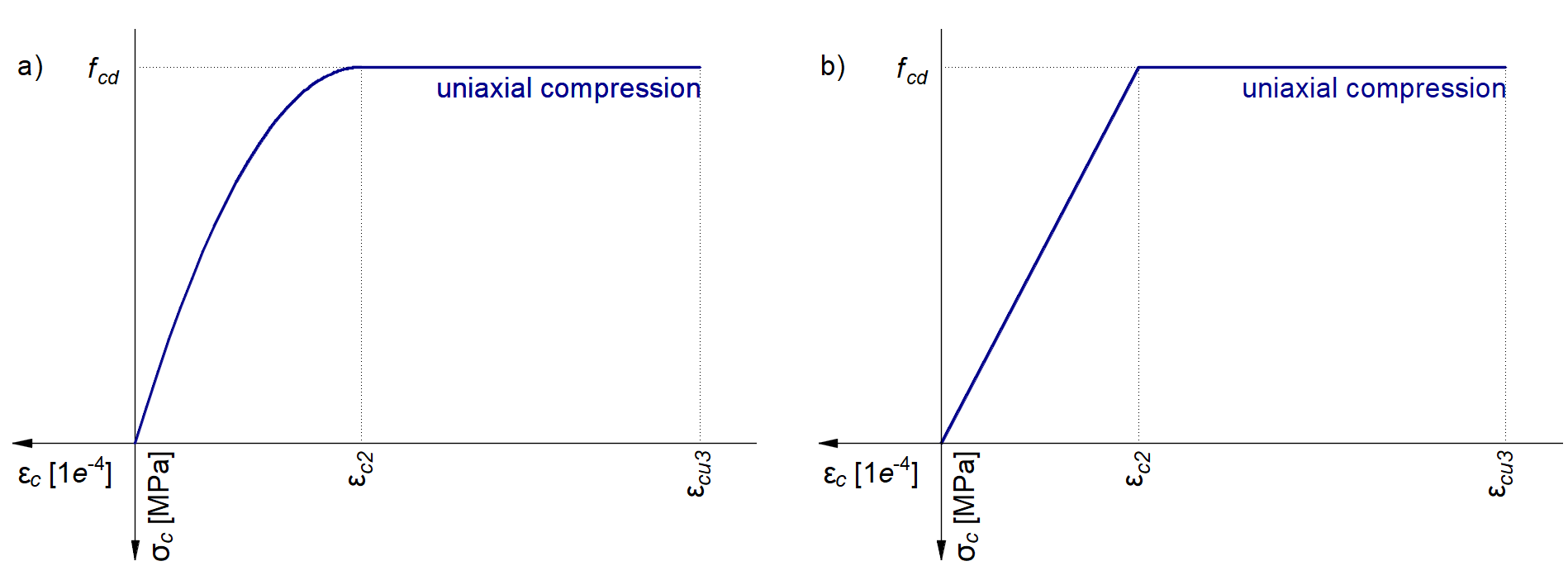
Das in 3D CSFM implementierte Betonmodell basiert auf den in EN 1992-1-1 für die Bemessung von Querschnitten vorgeschriebenen einachsigen Druckverformungsgesetzen, die nur von der Druckfestigkeit abhängen. Das Parabel-Rechteck-Diagramm, das in EN 1992-1-1 Cl. 3.1.7 (1) (Abb. 15a) vorgegebene Parabel-Rechteck-Diagramm wird in 3D CSFM standardmäßig verwendet, aber der Anwender kann auch eine vereinfachte elastisch-idealplastische Beziehung nach EN 1992-1-1 Cl. 3.1.7 (2) wählen (Abb. 15b). Die Zugfestigkeit wird vernachlässigt, so wie es bei der klassischen Stahlbetonbemessung der Fall ist.

\[ \textsf{\textit{\footnotesize{Abb. 15\qquad Die Spannungs-Dehnungs-Diagramme von Beton für GZT: a) Parabel-Rechteck-Diagramm; b) bilineares Diagramm}}}\]

Die Implementierung von 3D CSFM in IDEA StatiCa Detail berücksichtigt kein explizites Versagenskriterium in Form von Dehnungen für Beton in Kompression (d.h. nach Erreichen der Spitzenspannung wird ein plastischer Zweig mit ε_cu₂ (ε_cu₃) in einem Wert von 5% berücksichtigt, während EN 1992-1-1 von einer Bruchdehnung von weniger als 0,35% ausgeht). Mit dieser Vereinfachung lässt sich die Verformungskapazität von Strukturen, die auf Druck versagen, nicht nachweisen. Die Tragfähigkeit f_cdnach EN 1992-1-1 3.1.3 wird jedoch richtig vorhergesagt, wenn die Zunahme der Sprödigkeit des Betons bei steigender Festigkeit mit Hilfe des Abminderungsfaktors \(\eta_{fc}\) berücksichtigt wird, der im fib Model Code 2010 wie folgt definiert ist:

\[f_{cd}={\alpha_{cc}} \cdot \frac{f_{ck,red}}{γ_c} = {\alpha_{cc}} \cdot \frac{\eta _{fc} \cdot f_{ck}}{γ_c}\]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{ck}}}}} \right)^{\frac{1}{3}}} \le 1\]

wobei:

α_cc ist der Koeffizient zur Berücksichtigung von Langzeiteffekten auf die Druckfestigkeit und von ungünstigen Effekten, die sich aus der Art der Lasteinleitung ergeben. Er ist nach EN 1992-1-1 Cl. 3.1.6 (1). Der Standardwert ist 0,85.

f_ck ist die charakteristische Betonzylinderfestigkeit (in MPa für die Definition von \( \eta_{fc} \)).

Bewehrung

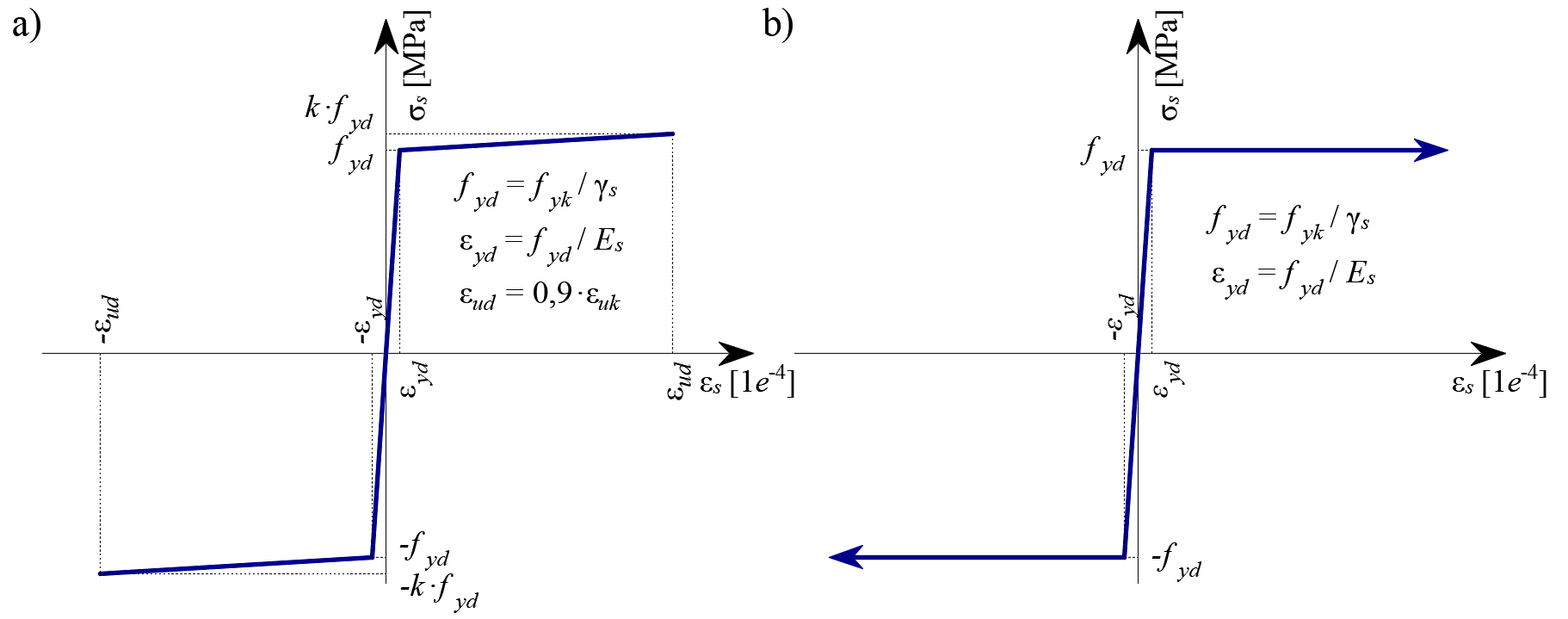
Standardmäßig wird das idealisierte bilineare Spannungs-Dehnungs-Diagramm für den Betonstahl nach EN 1992-1-1, Abschnitt 3.2.7 (Abb. 16) berücksichtigt. Die Definition dieses Diagramms setzt lediglich voraus, dass die grundlegenden Eigenschaften der Bewehrung bekannt sind (Festigkeits- und Duktilitätsklasse). Sofern bekannt, kann die tatsächliche Spannungs-Dehnungs-Beziehung der Bewehrung (warmgewalzt, kaltverformt, abgeschreckt und selbstvergütet, ...) berücksichtigt werden. Das Spannungs-Dehnungs-Diagramm der Bewehrung kann vom Benutzer definiert werden, aber in diesem Fall ist es unmöglich, die Mitwirkung des Betons zwischen den Rissen zu berücksichtigen. Die Verwendung des Spannungs-Dehnungs-Diagramms mit einem horizontalen oberen Zweig ermöglicht keinen Duktilitätsnachweis. Daher ist eine manuelle Überprüfung der Standard-Duktilitätsanforderungen erforderlich.

\[ \textsf{\textit{\footnotesize{Abb. 16 \qquad Spannungs-Dehnungs-Diagramm der Bewehrung: a) bilineares Diagramm mit geneigtem oberem Zweig; b) bilineares Diagramm}}}\] \[ \textsf{\textit{\footnotesize{mit einem horizontalen oberen Zweig}}}\]

Die Mitwirkung des Betons zwischen den Rissen (Abb. 17) wird automatisch berücksichtigt, indem die eingegebene Spannungs-Dehnungs-Beziehung des "nackten" Bewehrungsstabs geändert wird, um die durchschnittliche Steifigkeit der im Beton eingebetteten Stäbe (ε_m) zu erfassen.

\[ \textsf{\textit{\footnotesize{Abb. 17\qquad Schema der Spannungsaussteifung}}}\]

Teilsicherheitsfaktoren

Die in DIN EN 1992-1-1, Kap. 2.4.2.4 vorgeschriebenen Werte für die Materialsicherheitsfaktoren sind standardmäßig eingestellt, aber der Benutzer kann die Sicherheitsfaktoren in den Berechnungseinstellungen ändern.

\[ \textsf{\textit{\footnotesize{Abb. 18\qquad Die Einstellung der Materialsicherheitsfaktoren in Idea StatiCa Detail}}}\]

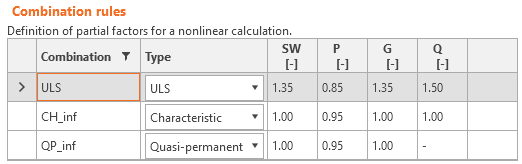
Lastsicherheitsbeiwerte müssen vom Benutzer in Kombinationsregeln für jede nichtlineare Kombination von Lastfällen definiert werden. Für alle in Idea StatiCa Detail implementierten Vorlagen sind die Teilsicherheits- und Kombinationsbeiwerte bereits vordefiniert.

\[ \textsf{\textit{\footnotesize{Abb. 19\qquad Die Einstellung der Teilsicherheitsbeiwerte in Idea StatiCa Detail}}}\]

Grenzzustand der Tragfähigkeit

Die GZT-Nachweise werden für die Betonfestigkeit, die Betonstahlfestigkeit und die Verankerung (Verbundschubspannungen) geführt.

Die Druckfestigkeit des Betons wird als Verhältnis zwischen der aus der FE-Analyse erhaltenen maximalen Vergleichsspannung σ_c_,eqund dem Grenzwert σ_c_,lim = f_cd bewertet.

Die äquivalente Hauptspannung drückt die äquivalente einachsige Spannung für einen allgemeinen dreiachsigen Spannungszustand aus.

\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]

Der σ_c_,eq-Wert kann daher direkt mit den Grenzwerten für die einachsige Festigkeit nach EN 1992-1-1 verglichen werden.

Dieser Ausdruck ergibt sich aus der Anwendung der Mohr-Coulomb-Plastizitätstheorie, wobei konservativ der innere Reibungswinkel φ = 0° angenommen wird .

Die Festigkeit der Bewehrung wird sowohl auf Zug als auch auf Druck als das Verhältnis zwischen der Spannung in der Bewehrung an den Rissen σ_sr und dem angegebenen Grenzwert σ_s_,lim bewertet:

\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{für bilineares Diagramm mit geneigtem oberen Ast}}\)

\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\textsf{\small{für bilineares Diagramm mit horizontalem oberem Ast}}\)

wobei:

f_yk ist die Streckgrenze der Bewehrung nach EN 1992-1-1 Cl. 3.2.3,

k ist das Verhältnis der Zugfestigkeit f_tk zur Streckspannung,
\(k = \frac{f_{tk}}{f_{yk}}\)

γ_sistder Teilsicherheitsbeiwert für die Bewehrung.

Die Verbundschubspannung wird unabhängig als das Verhältnis zwischen der durch FE-Analyse berechneten Verbundspannung τ_b und der Verbundendfestigkeit f_bdgemäß EN 1992-1-1, Kap. 8.4.2:

\[\frac{τ_{b}}{f_{bd}}\le 1\]

\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]

wobei:

f_ctdist der Bemessungswert der Betonzugfestigkeit nach EN 1992-1-1 Cl. 3.1.6 (2). Wegen der zunehmenden Sprödigkeit von höherfestem Beton ist f_ctk,0.05auf den Wert von C60/75 nach EN 1992-1-1 Cl. 8.4.2 (2) begrenzt.

η₁ ist ein Koeffizient, der von der Qualität des Verbundzustandes und der Lage des Stabes während des Betonierens abhängt (Abb. 31).

η₁ = 1,0, wenn "gute" Bedingungen erreicht werden und

η₁ = 0,7 für alle anderen Fälle und für Stäbe in Strukturelementen, die mit Gleitschalungen gebaut werden, es sei denn, es kann nachgewiesen werden, dass "gute" Verbundbedingungen bestehen

η₂ bezieht sich auf den Stabdurchmesser:

η₂ = 1,0 für Ø ≤ 32 mm

η₂ = (132 - Ø)/100 für Ø > 32 mm

\[ \textsf{\textit{\footnotesize{Abb. 20\qquad EN 1992-1-1 Abbildung 8.2 - Beschreibung der Verbundbedingungen}}}\]

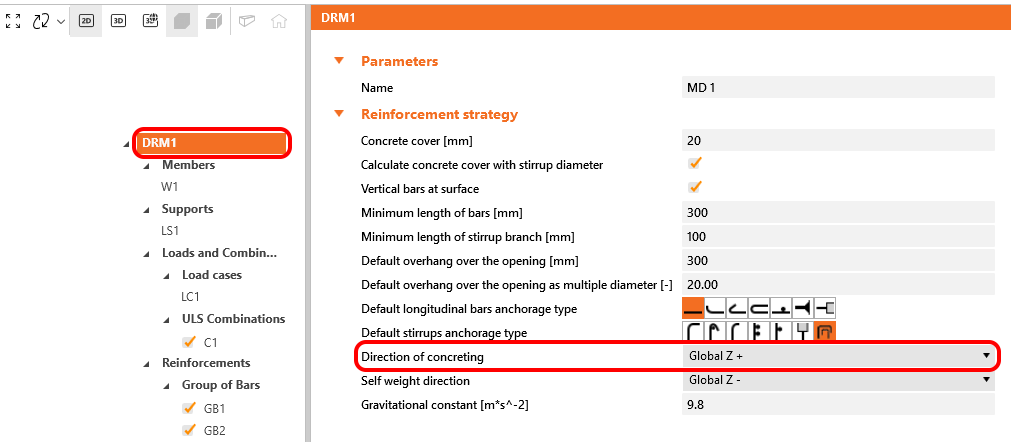
In IDEA StatiCa Detail werden die Verbundbedingungen gemäß Abb. 20 c) und d) berücksichtigt. Die Betonierrichtung kann in der Anwendung für jede Projektposition wie folgt eingestellt werden:

\[ \textsf{\textit{\footnotesize{Abb. 21\qquad Betonierrichtung}}}\]

Gesamtkraft F_tot und Grenzkraft F_lim

Die Gesamtkraft F_tot ist ein Ergebnis der Finite-Elemente-Analyse und kann auf zwei Arten definiert werden.

\[F_{tot}=A_{s}\cdot \sigma_{s}\]

wobei A_s die Fläche des Bewehrungsstabs und σ_s die Spannung im Stab ist.

Oder als Summe aus der Verankerungskraft F_aund der Verbundkraft F_bond.

\[F_{tot}=F_{a}+F_{bond}\]

wobei F_a die tatsächliche Kraft in der Verankerungsfeder und F_bond die Verbundkraft ist, die durch Integration der Verbundspannung τ_b über die Länge des Bewehrungsstabs l ermittelt werden kann.

\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]

C_s ist der Umfang des Bewehrungsstabs.

Die Grenzkraft F_lim ist die minimale Kraft im Element des Bewehrungsstabs unter Berücksichtigung der Tragfähigkeit des Bewehrungsstabs und der Verankerungsbedingungen (Verbund zwischen Beton und Bewehrung und Verankerungshaken, Schlaufen usw.).

\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]

\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]

\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]

\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]

wobei C_s der Umfang des Bewehrungsstabs und l die Länge vom Anfang des Bewehrungsstabs bis zum interessierenden Punkt ist.

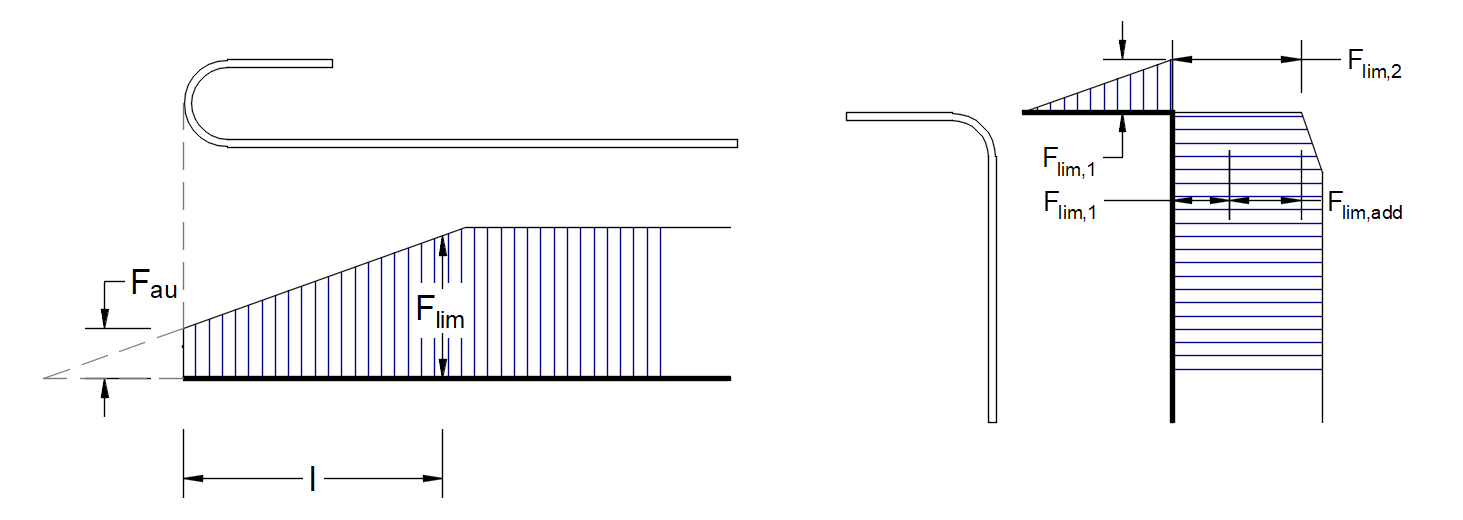
\[ \textsf{\textit{\footnotesize{Abb. 22\qquad Definition der Grenzkraft Flim}}}\]

\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]

wobei F_lim,add die zusätzliche Kraft ist, die aus der Größe des Winkels zwischen benachbarten Elementen berechnet wird. F_lim,2 muss immer kleiner als F_u sein.

Zu den verfügbaren Verankerungstypen in 3D CSFM gehören ein gerader Stab (d.h. keine Reduzierung der Ankerenden), ein gebogener Stab, ein Haken, eine Schlaufe, ein geschweißter Querstab, ein perfekter Verbund und ein durchgehender Stab. Alle diese Typen sind zusammen mit den jeweiligen Verankerungsbeiwerten β in Abb. 23 für die Längsbewehrung und in Abb. 24 für die Bügel dargestellt. Die Werte der angenommenen Verankerungsbeiwerte entsprechen EN 1992-1-1 Abschnitt 8.4.4 Tab. 8.2. Es ist zu beachten, dass 3D CSFM trotz der verschiedenen Möglichkeiten drei Arten von Verankerungsenden unterscheidet: (i) keine Verringerung der Verankerungslänge, (ii) eine Verringerung der Verankerungslänge um 30% im Falle einer normalisierten Verankerung und (iii) perfekter Verbund.

\[ \textsf{\textit{\footnotesize{Abb. 23\qquad Verfügbare Verankerungstypen und entsprechende Verankerungsbeiwerte für Längsbewehrungsstäbe im 3D-CSFM:}}}\]

\[ \textsf{\textit{\footnotesize{(a) gerader Stab; (b) Biegung; (c) Haken; (d) Schlaufe; (e) geschweißter Querstab; (f) perfekte Verbindung; (g) durchgehender Stab}}}\]

\[ \textsf{\textit{\footnotesize{Abb. 24\qquad Verfügbare Verankerungstypen und entsprechende Verankerungsbeiwerte für Bügel.}}}\]

\[ \textsf{\textit{\footnotesize{Geschlossene Steigbügel: (a) Haken; (b) Biegung; (c) Überlappung. Offene Steigbügel: (d) Haken; (e) durchgehender Stab}}}\]

Um die Anforderungen von EN 1992-1-1 zu erfüllen, sollte die Verankerungsfeder in der Berechnung verwendet werden. Die Verankerungsfeder wird durch den Beiwert β modifiziert, so dass der Benutzer bei der Definition der Anfangs- und Endbedingungen der Bewehrung eine der verfügbaren Verankerungsarten verwenden muss.

Testen Sie die neueste IDEA StatiCa Version noch heute

Testen Sie IDEA StatiCa kostenlos

Verifizierungen und Validierungen

Einzelprüfung: Verankerung

Einzelprüfung: Einfacher Biegeversuch an Auslegern

Einzelprüfung: Scherversuche an Trägern mit geringen Bügelmengen

Triaxiale Beanspruchung - der aktive Umschnürungseffekt

Stützen, die einer hohen Druckbelastung ausgesetzt sind - Passive Umschnürungswirkung

Auszugsverhalten von Ortbetonankern mit unterschiedlichen Verankerungstiefen

Referenzen

Wu, , D.; Wang, Y.; Qiu, Y.; Zhang, J.; Wan, Y.-K. Determination of Mohr–Coulomb Parameters from Nonlinear Strength Criteria for 3D Slopes. Math. Probl. Eng. 2019, 6927654.
Lelovic, S.; Vasovic, D.; Stojic, D. Determination of the Mohr-Coulomb Material Parameters for Concrete under Indirect Tensile Test. Tech. Gaz. 2019, 26, 412–419.
Galic, M.; Marovic, P.; Nikolic, Ž. Modified Mohr-Coulomb—Rankine material model for concrete. Eng. Comput. 2011, 28, 853–887.
Fan, Q.; Gu, S.C.; Wang, B.N.; Huang, R.B. Two Parameter Parabolic Mohr Strength Criterion Applied to Analyze The Results of the Brazilian Test. Appl. Mech. Mater. 2014, 624, 630–634.